AtCoder Beginner Contest 184 题解

Problem A - Determinant

按题意来进行直接计算

时间复杂度：#card=math&code=%5Cmathcal%7BO%7D%281%29)

int main() {
    ios_base::sync_with_stdio(false), cin.tie(0);
    int a, b, c, d;
    cin >> a >> b >> c >> d;
    cout << a * d - b * c;
    return 0;
}

Problem B - Quizzes

模拟

时间复杂度：#card=math&code=%5Cmathcal%7BO%7D%28N%29)

int main() {
    ios_base::sync_with_stdio(false), cin.tie(0);
    int N, X;
    string S;
    cin >> N >> X >> S;
    for (auto c : S) {
        if (c == 'x' and X > 0) X--;
        else if (c == 'o')
            X++;
    }
    cout << X << "\n";
    return 0;
}

Problem C - Super Ryuma

题意：

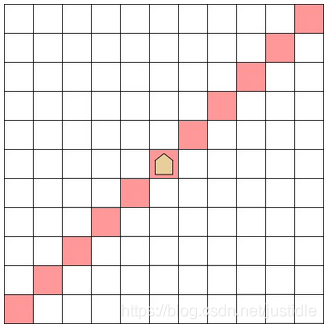
有一个无限的二维网格，在坐标 (r1, c1) 处有一个超级龙马，每次这个超级龙马可以移动如上图的位置。更加准确的说，当超级龙马在坐标 (a, b)，它可以移动到坐标 (c, d) 只要满足下面的条件：

请找出从 $(r1, c1) $ 移动到 #card=math&code=%28r2%2C%20c2%29) 的最少的移动步数。

这里引用一下 努力的老周 的解法：

先分析移动方法

规则一：

当前位置为 #card=math&code=%28a%2C%20b%29)。

1、我们向右下移动一格，对应的坐标为 #card=math&code=%28a-1%2C%20b%2B1%29)；

2、我们向右下移动 n 格，对应的坐标为 #card=math&code=%28a-n%2C%20b%2Bn%29)；

3、我们向左上移动一格，对应的坐标为 #card=math&code=%28a%2B1%2C%20b-1%29)；

4、我们向左上移动 n 格，对应的坐标为 #card=math&code=%28a%2Bn%2C%20b-%20n%29)；
我们可以发现，满足条件 c+d=a+b，也就是满足条件一。也就是副对角线方向运动，如下图所示。

规则二：

当前位置为 #card=math&code=%28a%2C%20b%29)。

1、我们向左下移动一格，对应的坐标为 #card=math&code=%28a%2B1%2C%20b%2B1%29)；

2、我们向左下移动 n 格，对应的坐标为 #card=math&code=%28a%2Bn%2C%20b%2Bn%29)；

3、我们向右上移动一格，对应的坐标为 #card=math&code=%28a-1%2C%20b-1%29)；

4、我们向右上移动 n 格，对应的坐标为 #card=math&code=%28a-n%2C%20b-%20n%29)；

我们可以发现，满足条件 c-d=a-b，也就是满足条件二。也就是主对角线方向运动，如下图所示。

规则三：

自然就是图片中中间部分。如下图所示。

下面我们根据这个来分析一下样例数据。

样例数据 1

根据样例数据 1，我们需要从 (1, 1) 到 (5, 6)。

先用规则二，沿着主对角线移动，从 (1, 1) 移动到 (5, 5)；

再用规则三，从 (5,5) 移动到 (5, 6)。

样例数据 2
根据样例数据 2，我们需要从 (1, 1) 到 (1, 200001)。

先用规则二，沿着主对角线移动，从 (1, 1) 移动到 (100001, 100001)；

再用规则一，沿着副对角线移动，从 (100001, 100001) 移动到 (1, 200001)。

样例数据 3
根据样例数据 3，我们需要从 (2, 3) 到 (998244353， 998244853)。

先规则三，从 (2,3) 到 (3, 3)；

再用规则一，沿着副对角线移动，从 (3, 3) 到 (-247, 253)；

再用规则二，沿着主对角线移动，从 (-247, 253) 移动到 (998244353， 998244853)。

根据上面的分析，我们可以总结出，从 (r1, c1) 移动到 (r2, c2)，超级龙马的移动可能有以下几种可能：

移动次数为 0 次：起点坐标和终点坐标重合，即 r1==r2 && c1==c2

移动次数为 1 次：

也就是超级龙马可以根据任意一条规则从 (r1, c1) 移动到 (r2, c2)。这样，有三条规则可以满足这个要求。

根据规则一，可以得到条件为 r1+r2==c1+c2；

根据规则二，可以得到条件为 r1-r2==c1-c2;

根据规则三，可以得到条件为 abs(r1-r2)+abs(c1-c2)<=3。

移动次数为 2 次：

这是一个组合问题，也就是超级龙马要使用两次规则。我们可以通过遍历也就是先按照规则三移动一次，再判断利用其他规则能否到达目的地即可。具体的实现可以参看下面的 AC 代码。

还有一个特殊情况是起点坐标之和和终点坐标之和奇偶性相同。参考样例输入 2。

移动次数为 3 次：剩下的情况就移动三次肯定可以到达。

个人做的时候的分析：

1. 起点和终点重合，总步数为 。
2. 一步可到达（共对角线或曼哈顿距离不超过 ），总步数为 。
3. 走两次对角线，设此时中间点为#card=math&code=%28r%2Cc%29)，可得到关于 和 的二元一次方程组，判断其是否有整数解（其实就是判断奇偶）。如果有整数解，总步数为 。
4. 枚举起点的邻近点，然后判断是否一步可到达。如果可到达，则总步数为 。
5. 其他所有情况都可以通过移动到一个相邻的格子转化为第三种情况，从而总步数为 。

时间复杂度 #card=math&code=%5Cmathcal%7BO%7D%281%29)。

using ll = long long;
int main() {
    ios_base::sync_with_stdio(false), cin.tie(0);
    ll a, b, c, d;
    cin >> a >> b >> c >> d;
    c -= a, d -= b;
    c = llabs(c), d = llabs(d);
    if (c == 0 && d == 0) cout << 0 << "\n";
    else if (c == d || c + d <= 3)
        cout << 1 << "\n";
    else if ((c + d) % 2 == 0 || c + d <= 6 || llabs(c - d) <= 3)
        cout << 2 << "\n";
    else
        cout << 3 << "\n";
    return 0;
}

Problem D - increment of coins

题意：一个包里包含 X 个金币、Y 个银币、Z 个铜币。在包里钱币满足相 同颜色达到 100 之前，我们可以重复以下动作：随机选一种钱币，取出一枚， 再放入相同颜色钱币两枚。找出完成这些操作的期望值。

根据题目的意思，其实就是每次向包里随机加入一枚钱币，直到包里某种钱币数量达到 100。本题的核心是如何计算期望。本题属于标准的动态规划求期望问题。直接套用模板即可。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e2 + 10;
double dp[N][N][N];
int main() {
    ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
    int a, b, c;
    cin >> a >> b >> c;
    for (int i = 99; i >= a; i--)
        for (int j = 99; j >= b; j--)
            for (int k = 99; k >= c; k--) {
                // 令 t = x + y + z，减少代码量
                double t = i + j + k;
                dp[i][j][k] = i / t * (dp[i + 1][j][k] + 1) +
                              j / t * (dp[i][j + 1][k] + 1) +
                              k / t * (dp[i][j][k + 1] + 1);
            }
    cout << fixed << setprecision(9) << dp[a][b][c] << endl;
}

这道题是去年写过一次：Here.

Problem E - Third Avenue

经典BFS，但要注意同一种类型的传送点只考虑一次。

using ll = long long;
const int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, -1, 0, 1};
const int INF = 0x3f3f3f3f;
int H, W;
int main() {
    ios_base::sync_with_stdio(false), cin.tie(0);
    cin >> H >> W;
    vector<string> a(H);
    int si, sj, gi, gj;
    vector<vector<pair<int, int>>> tele(26);
    for (int i = 0; i < H; ++i) {
        cin >> a[i];
        for (int j = 0; j < W; ++j) {
            if (a[i][j] == 'S') si = i, sj = j;
            if (a[i][j] == 'G') gi = i, gj = j;
            if (a[i][j] >= 'a' && a[i][j] <= 'z')
                tele[a[i][j] - 'a'].emplace_back(i, j);
        }
    }
    vector<bool> vis(26);
    vector<vector<int>> dist(H, vector<int>(W, INF));
    dist[si][sj] = 0;
    queue<pair<int, int>> q;
    q.emplace(si, sj);
    while (q.size()) {
        auto [i, j] = q.front();
        q.pop();
        if (i == gi and j == gj) {
            cout << dist[i][j] << "\n";
            return 0;
        }
        for (int k = 0; k < 4; ++k) {
            int ni = i + dx[k], nj = j + dy[k];
            if (ni < 0 or ni >= H or nj < 0 or nj >= W or dist[ni][nj] != INF or
                a[ni][nj] == '#')
                continue;
            dist[ni][nj] = dist[i][j] + 1;
            q.emplace(ni, nj);
        }
        if (a[i][j] >= 'a' and a[i][j] <= 'z' and !vis[a[i][j] - 'a']) {
            vis[a[i][j] - 'a'] = true;
            for (auto [ni, nj] : tele[a[i][j] - 'a']) {
                if (dist[ni][nj] == INF) {
                    dist[ni][nj] = dist[i][j] + 1;
                    q.emplace(ni, nj);
                }
            }
        }
    }
    cout << -1 << "\n";
    return 0;
}

Problem F - Programming Contest

meet−in−the−middle（又称折半搜索、双向搜索）对于的搜索类型题目，一般都可以采用该算法进行优化，很稳很暴力。

我们可以将n分成2部分这样可以将 对于 的可以将复杂度降到 左右 ;
然后我们通过dfs将前半段和后半段的所有不大于T的数存起来，在枚举一个的时候，判断另一个。

#include <bits/stdc++.h>
using namespace std;
const int N = 1 << 20, M = 1e9 + 7;
const int INF = 0x7fffffff;
int n, m, T;
int a[N], b[N], c[N];
void dfs(int l, int r, int v, int d[], int &num) {
    if (v > T) return;
    if (l == r) {
        d[++num] = v;
        return;
    }
    dfs(l + 1, r, v + a[l], d, num);
    dfs(l + 1, r, v, d, num);
}
int main() {
    ios_base::sync_with_stdio(false), cin.tie(0);
    cin >> n >> T;
    for (int i = 1; i <= n; i++) cin >> a[i];
    sort(a + 1, a + n + 1);
    int len = n / 2 + 1, b_num = 0;
    dfs(1, len, 0, b, b_num);
    sort(b + 1, b + b_num + 1);
    int c_num = 0;
    dfs(len, n + 1, 0, c, c_num);
    sort(c + 1, c + c_num + 1);
    int ptr = c_num, maxn = 0;
    for (int i = 1; i <= b_num; i++) {
        while (b[i] + c[ptr] > T) ptr--;
        maxn = max(maxn, b[i] + c[ptr]);
    }
    cout << maxn << "\n";
    return 0;
}

另外可以使用set容器，比较慢

#include <iostream>
#include <set>
#include <vector>
using namespace std;
typedef long long ll;
int main() {
    int n, t;
    cin >> n >> t;
    vector<int> a(n);
    for (int i = 0; i < n; ++i) cin >> a[i];
    set<int> L, R;
    L.insert(0), R.insert(0);
    int l = n / 2, r = n - l;
    for (int i = 0; i < (1 << l); ++i) {
        int s = 0;
        for (int j = 0; j < l; ++j) {
            if (i & (1 << j)) s += a[j];
            if (s > t) break;
        }
        if (s <= t) L.insert(s);
    }
    for (int i = 0; i < (1 << r); ++i) {
        int s = 0;
        for (int j = 0; j < r; ++j) {
            if (i & (1 << j)) s += a[l + j];
            if (s > t) break;
        }
        if (s <= t) R.insert(s);
    }
    int ans = 0;
    for (int li : L) {
        auto it = R.lower_bound(t + 1 - li);
        if (it != R.begin()) --it;
        if (li + *it <= t) ans = max(ans, li + *it);
        if (ans == t) break;
    }
    cout << ans << endl;
}