《系统化思维导论》

概念

有了解决问题的思路与方法，兴致勃勃的去思考和解决生活或工作中面临的问题，但是很可能发现会导致一些新的问题，为什么解决了一个问题引入了另外一个问题？ 因为缺乏系统思考。系统思考可以让我们更好，更稳健，更睿智的决策。

想要系统思考，我们需要拓展自己的视野，同时关注忽略细节，既见树木，又见森林。把问题进行割裂研究是系统思考最大的阻碍。

系统思考：处理真实世界中复杂问题时用整体的观点观察周围的事事物。

系统：一堆相互连接的实体

连接：即存在某种关系，比如在马路上随便圈一些人，这些人就没有很好的连接。在工作中，推动项目发展的团队，这些人之间就有特殊的连接。

连接概念说明：

我们手握一枚硬币，直接松手，会发生的事情是它掉在地上。但是如果是把一种产品的价格降低了5%，可能导致的事销量增长，到可能触发价格战，可能一些顾客失去了奢侈品的感觉… 所有这些都算一个单一事件带来的可能后果。

扔一枚硬币时：环境非常简单，这一事件涉及的实体只有自己，硬币和地面。

产品降价时：整个环境迥然不同，很多实体被牵扯其中，它们被各种不同的联系连接在一起，由于连接的存在，事件可能会不断的传递下去。

系统特性：整体大于局部之和

有许多东西只有在一个系统是完整的时候才表现出来的特性。

单只鸟无法排成队列，一群鸟可以排成V字形或者其它形状，并且保持不变。单个人做的东西有限，团队在一起才能做更多的事情。飓风由水分子组成，普通的水分子无什么影响，但是许多微小的水分子一起配合，共同形成了一致的，威力惊人的宏观结构。

规律

任何模型，都是用我们认为已经了解的一种东西，去表示我们认为想要了解的另一种东西。

定律的模式一般为：“如果….那么….”，我们常常忘记它是有条件的，因为这些定律的表达方式比较简单，即省略了”如果…”部分，这部分写出来，定律就太长了。例如：

热力学第一定律：系统中的总能量守恒

这个表述可以进一步细化：“如果系统中的能量既没有进，也没有出，那么每次策略都会得到相同的值。”，在这一部基础上还可以进行细化，但如果再细化，情况更糟了，更难记住。

要学习科学的思维，不只要记住规律，而是要知道什么时候已经什么方式运用规律。

定律保护定律：如果事实和定律相冲突，那么拘谨接受事实或者改变定义，但是绝不要抛弃定律

出于某种未知的心理学原因，最好记的定律采用禁止、矛盾、甚至是悖论的表述方式。能量守恒定律的另一种表达方式是：

不可能造出永动机

许多规律都会有多种表达方式，作为定义，作为测量方法，作为探索工具，特别是更容易记住的否定形式。任何自诩为定律的，至少要有两种适应情况：一种是该定律的来源，另一种作为保险。

一个组合错误案例：

我在桥上朝河里吐口水，发现河水的纯度没有明显的变化后，我去了投票站，给发行市政债券用以新建河水处理工厂的提议投了反对票。

一个分解错误案例：

我站在桥上，发现河水很干净，所以我的结论是，没有人向河里吐口水。

组合定律：整体大于部分之和

分解定律：部分大于整体的局部

观察者与观察结果

人们观察同一件事情，或者同一个事物，却经常得出不同的结果，这是为什么呢？系统化思维导论中提到了一种数学化的解释。

观察者所做的事情是观察。外部的世界可以理解为一个系统，系统是可以理解为物体的集合，一次观察可以表述为从一个集合中选择一个或多个元素。

观察者一般有自己的观察类型，比如对衣衫和边幅不修的类型进行观察，视野范围可以标识为：

{衣衫，边幅不修}

作为观察者，视野范围中的每一个元素可以再次推导出可能的选择范围，如：

衣衫：{细麻布、束带、袖口、丝带、裙子、鞋带}  -> 6个，可以更多
边幅不修：{随风飘舞、纷纷扬扬、疏忽、潇洒、随意拂袖}  -> 5个，也可以更多

然后我们可以对集合进行处理，组织描述。

观察者的一次完整观察，就是对观察范围内的集合做一次选择，对于上述的{衣衫、边幅不修}，可能的组合有笛卡尔积 6*50=30种可能。

如果对看到的每一件事都运用笛卡尔积，很快就会产生大量的集合，而这么多种的可能性需要的计算量，很难达到。在观察者模型中，要时时提醒自己，需要多大的计算能力。

在表达时，大家看到的是一样的，但是表述出来的给人的感觉是不一样的，如果有时间，我们可以审视下自己观察到的结果是什么，能不能有更好的组织方式。

学科思维

带来麻烦的不是未知的东西，而是我们以为知道，实际却并非如此的东西。

简化思维

力学系统一般由几个不同的部分组成，每部分之间都会存在一定的相互作用力，也许物理学家能写出方程，但却不求解，虽然告诉的计算机系统拓展了力学系统求解的范围，但是仍然有很多无法求解的。

随着问题规模的增加，计算量将成倍的增加。如果方程数增加2倍，必须采用快4倍的计算机，10个物体租车的系统存在2^10=1024个方程。

我不知道他人如何，我自己一般在开始时就放弃了，对于那些每天都能遇到的最简单的问题，我一视图深入思考，就感觉无法回答。

牛顿在万有引力定律中提供了一种重要的简化方式，这一定律被誉为迄今为止人类最了不起的归纳。

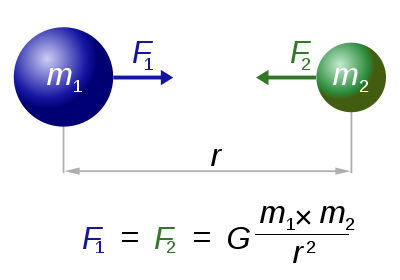
牛顿是一个添加，不是因为他的大脑具有超级计算能力，而是因为他会简化和理想化，是普通人的大脑在一定程度上能认识这个世界。

在太阳系中，太阳的质量比其他的星球所有的质量之和还要打，这样一个占主导地位的天体，那些没有太阳参与的两两之间的作用力就可以小的忽略了。

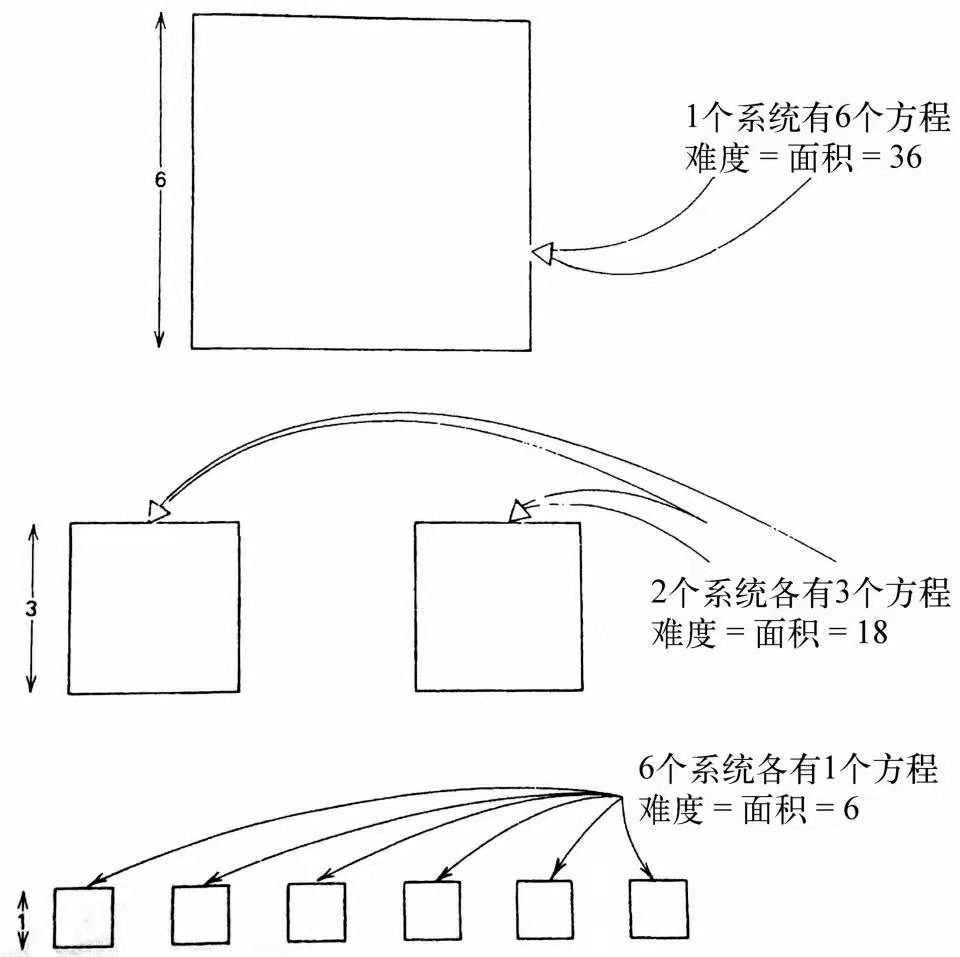
通过不断的分解，我们可以将36个方程减为6个。

随机思维

在描述气体这种数量非常多的物体时，机械力学显得力不从心，就算只关心物体的两两作用，仍然无法求解。

科学家假定气体是由分子组成，但需要解释这种信念与观测到气体特性的关系。他们的做法是观测一些分子的平均特性，而不是某个分子的特性。

分子的量非常的大，满足所谓的大数定律：

观测的样本数量越多，观测值越接近预测的平均值

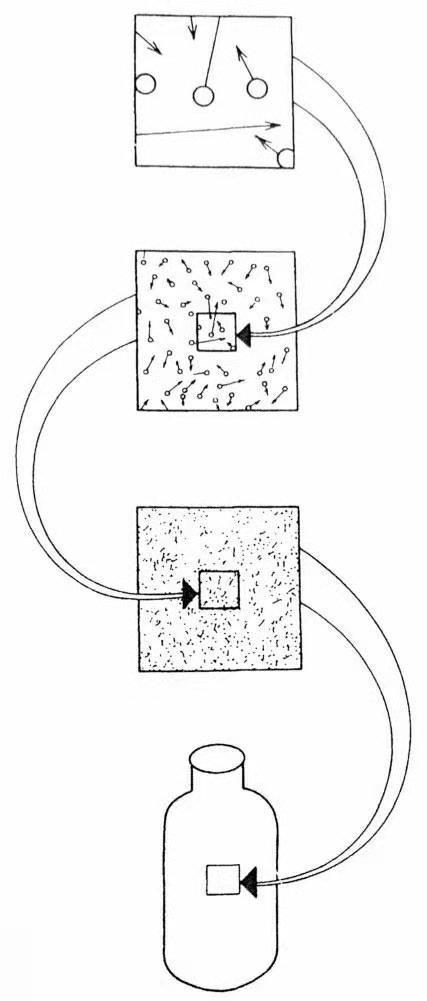
上面这两张图证明了，在整体中随机抽取一部分可近似预测到整体的行为。

统计力学与机械力学的关系：

• 统计力学面对的是无序的复杂，即系统本身非常复杂，因此具有足够的规律性，可以进行统计研究

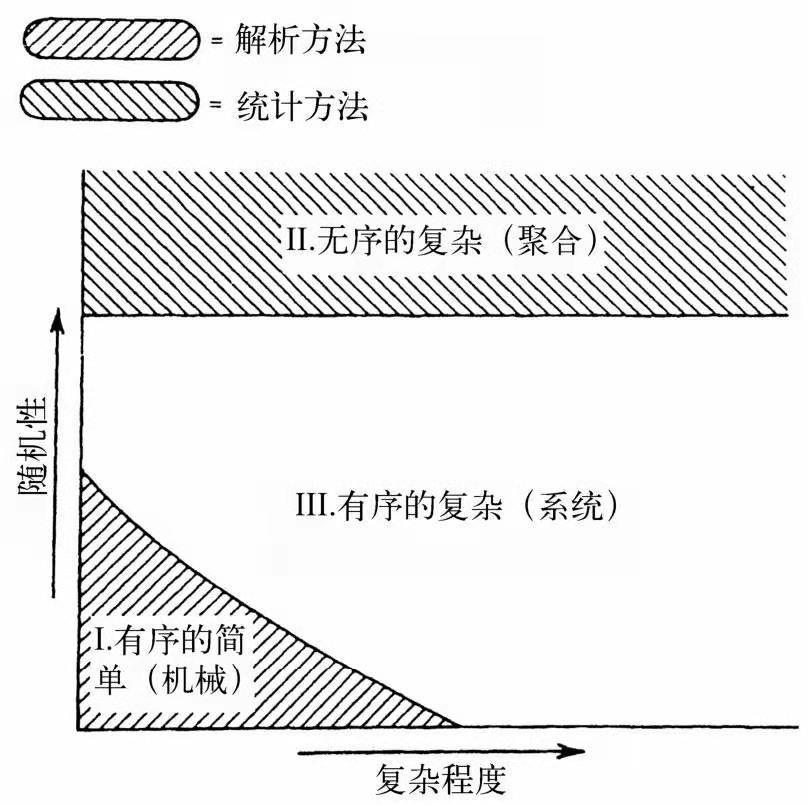
• 区域1成为有序的简单，属于机械力学的范围， 可对物体进行简化
• 区域2是无序的复杂，属于种群或者集合的范围，可以采用样本
• 区域3，有序的复杂，则是系统的研究领域

中数定律

中数定律的重要性不在于他的预测能力，而在于它的应用范围，好的机械力学系统和统计学实际上很少，包围着我们的其实是中数系统。

• 计算机的部件个数是中数
• 细胞中酶的数量是中数
• 组织机构里的人数是中数
• 人们的词汇量是中数
• …