如何理解动态规划

两个例子

按照定义，动态规划是把一个大问题拆解成一个一个的小问题，但是一个大问题之所以能够使用动态规划去解决并不是因为它能拆解成小问题，而是取决于该问题是否能用动态规划解决的是这些”小问题“会不会被被重复调用。
举个例子：计算n，n+m的阶乘。这对于我们来说都是很小菜一碟的，采用循环、递归都能很快的求解出来，但是对于一个程序，当我要计算n的阶乘的时候程序会从1—n计算一遍，当我还想知道n+1的阶乘时，程序会重新计算1—n+m，那么是不是感觉到这个过程就很浪费时间呢？于是我们就想：当我们知道n的阶乘的时候，那么n+m的阶乘就能少做一些重复性的步骤，而是只需要n—n+m的阶乘，因为n的阶乘已经知道了。动态规划就是这个思想，保存每个状态的值以供后续调用，从而减少做重复计算。正是一种以空间换时间的策略。
进一步考虑，上例中的n，n+m的阶乘如果换成了其他的最优化问题，当我们想知道n+m这个问题的最优解时只需要知道n到n+m这个问题的解就行了。

再举个例子：这个例子可能还有点抽象，借鉴知乎上一个高赞回答：有n个阶梯，一个人每一步只能跨一个台阶或是两个台阶，问这个人一共有多少种走法？
那当我们知道了5-10台阶走法的路径数，我们将其记录下来。当我们计算3-10台阶走法的路径数的时候只需要计算3-5加上已经保存的5-10的路径数。因为不管我是从3走过来的，还是从4走过来的，走到5之后，存在的路径就是第一次计算出的结果，也就无需重复计算！
如果采用暴力求解的话，肯定在计算3-10时计算一遍5-10，计算4-10时再计算一遍5-10，进行了很多重复性的计算，那当问题规模很大的时候，显然是个非常耗时的做法，这也正是体现出了动态规划的意义。

一个例子理解贪心，穷举与动态规划

我们面对的是一个求最优解或统计之类的问题，这个问题基于“我们要模拟完成一个大任务”，这个大任务可以分成若干步骤，每个步骤有若干种决策，每个步骤完成后，就到达了一个阶段性状态。
比如，你要从A地到Z地，没有直达，所以第一步需要到一个中间地点，比如H或I，第二步再前进，比如到P或Q，最后到达Z，每一步有若干决策，大致就是这样一个模型。你大概发现问题了，如果第一步到H和I都可以，第二步到P和Q都可以，那我每一步只选最优，这就是贪心算法。但是前提是：每个阶段状态跟决策无关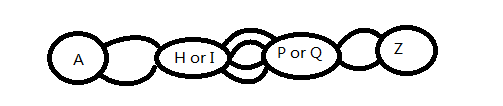

然而现实情况可能是，你第一步的选择会影响后面的分支，比如你第一步可以选择到H或I，但是到了H后，你只能选择经过P或Q到Z了，而如果到了I，你只能选择R或S到Z，这样一来，即便第一步到H或I你选择了较好的一条路，也不保证最终结果最优，因为比如你选了H，那万一I-R-Z的路要比H开始到Z的路径短了更多，最优路径可能是A-I-R-Z，所以你要把这些路都尝试一遍，才知道哪个最优，这种做法也就是穷举。

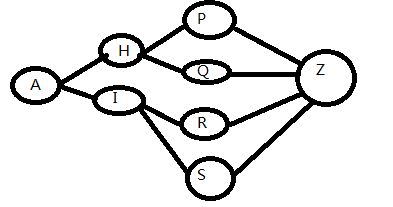
我们稍微修改一下题设，假如从I出发并不是到R和S，而是到Q或R，如下图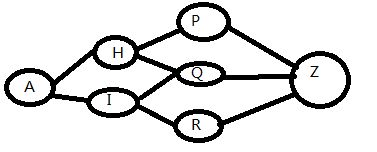

当然，我们可以用穷举解决所有的动态规划问题。但是，我们可以有更快的做法，我们并不用将A-H-Q-Z和A-I-Q-Z两条路单独计算，因为他们有公共子集A->Q.结合图一，我们可以清晰地感觉到只需要计算到每个有共同状态的位置求各阶段的最优，最后每个阶段选最优组合然后使用贪心算法组合起来就行。因此我们可以先得到A->Q中最短的，然后将Q->Z中最短的结合起来（此处只有一条路，假设有很多条路径）。这样就大大的降低了遍历次数。
因此，我们可以从A开始，向Z进行BFS，并对BFS中每个点保存最优状态，如果有不同的路径BFS到了同一个点，留最好的一条就行，比如上面这个，你的算法可能先从A-H-Q搜到了Q这个位置，之后从A-I-Q又到了这里，留最好的一条，最后一轮从PQR三个点到Z，就结束了。
学到这，我们已经大致了解了什么是动态规划，只是七窍通了六窍—还有一窍不通。稍微有点感觉，就是那种说不出的感觉。会？不，我不会。不会？不，我明白一丢丢。别慌，古语有云：talk is cheap，show me the code。下面结合例子，来真正的揭开动态规划的面纱。

动态规划解题过程

首先，动态规划问题的一般形式就是求最值。既然是求最值，那么动态规划的核心问题就是穷举。穷举出所有可能性，才能再其中找到最值。当然，如果只是简单的穷举，肯定不会起一个这么高大上的名称。因为动态规划的问题存在重叠子问题，所以动态规划的穷举有点不一样，它不是单纯的暴力穷举，而是采用了一些小trick，比如备忘录或者DP table。这样也就起到了一种以空间换时间的高效解法。
既然动态规划的核心思想是穷举求最值，但是问题千变万化，穷举所有的可行解并不是一件容易的事，所以我们也就明白了动态规划的核心问题【建立状态转移方程】。这一步是最重要也是最难的。
下面是一个求解问题的思维框架：
明确 base case -> 明确「状态」-> 明确「选择」 -> 定义 dp 数组/函数的含义

# 初始化 base case
dp[0][0][...] = base
# 进行状态转移
for 状态1 in 状态1的所有取值：
    for 状态2 in 状态2的所有取值：
        for ...
            dp[状态1][状态2][...] = 求最值(选择1，选择2...)