322 coin-change 零钱兑换

动态更新bing图片

力扣索引

322. 零钱兑换 Medium

原始问题

You are given coins of different denominations and a total amount of money **amount. Write a function to compute the fewest number of coins that you need to make up that amount. If that amount of money cannot be made up by any combination of the coins, return -1.You may assume that you have an infinite number of each kind of coin.
给定不同面额的硬币 coins和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回 -1。你可以认为每种硬币的数量是无限的。
Input：coins = [1, 2, 5], amount = 11
Output：3
Explanation：11 = 5 + 5 + 1
下面我将以下图举例说明，其中amount=11,coins=[1,2,3],很显然我们在脑海中轻轻的过一遍就能想出由三个面额为3的硬币加上一个面额为2的硬币就组成了最优的答案：4枚、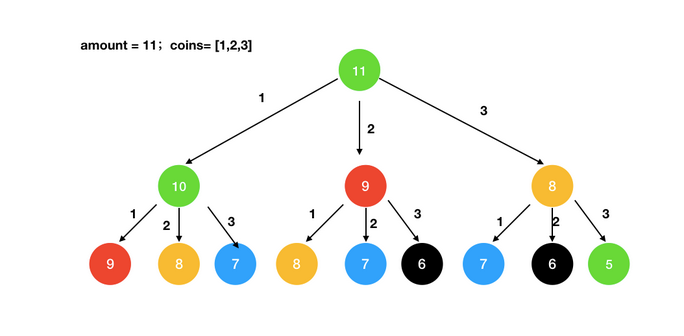

贪心不可取

首先这种题目，很多人会想到采用贪心算法的方式来解决。也就是先对整个硬币进行排序，然后看总额能够满足多少枚大面值的硬币，循环完所有面值的硬币，就能得到结果，代码如下：

# LeetCode
# 这种做法是错误的
class Solution:
    def coinChange(self, coins: List[int], amount: int) -> int:
        ans=0
        coins.sort(reverse=True)
        for i in coins:
            if amount==0:return ans
            temp,amount=divmod(amount,i)
            ans+=temp
        return -1 if amount!=0 else ans

这种做法在某些特殊的情况下是可行的，但是这种做法在绝大多数的情况下是不可行的。举个例子：amount=13,coins=[1,4,5]，用贪心法得到的最短序列是5 5 1 1 1，最少硬币数是5。而其实本题最优解时4 4 4 1，最少硬币数是4。所有看出来贪心的问题了吗。
那什么时候是可行的呢？当然有很多特殊的例子啊，能够求出正确解的都是可行的，哈哈哈。我自己想到一种比较特殊的例子：从1开始的递增序列作为硬币面额。

暴力匹配

深度优先搜索DFS

首先，这题一定要明确节点和边分别是什么。也就是后文中动态转移方程的状态和策略。一定要抓住主线金额，既然想求组成11元金额硬币的最小组成策略，那我们拿掉其中一个硬币后子问题也要上最优的，比如说拿掉一个一元的，就是求组成10元金额硬币的最小组成策略。一定要搞懂这个问题，后面还会再次提到，所以我们的节点是金额，边则对应各硬币的面额。
我们再次仔细看一眼上面的流程图，有没有什么感觉？没感觉继续看，这不就是一颗三叉树吗？那递归是什么，不就是遍历所有树中的节点吗？对于三叉树那肯定不能使用前中后序遍历，但是不影响我们使用层次遍历啊。（这个地方跟层次还有点不同，以便后续计算。输入是按层次输入，但是输出却不是采用队列的结构进行先进先出）。可以称之为层次遍历的变体，自己瞎起的名字哈哈哈。这是啥，我的天哪，这不就是DFS真的是后知后觉，不知道DFS是啥的详见图论中图的两种遍历算法那节。

# jupyter notebook
def coinChange2(coins, amount):
    def digui(amount):
        if amount==0:return 0
        if amount<0:return -1
        res=int(1e9)                                    
        for i in coins:                   #每个金额都遍历所有的金币
            subproblem=digui(amount-i)       #递归调用
            if subproblem!=-1:res=min(res,subproblem+1)
        return res if res != int(1e9) else -1
    return digui(amount)
coins = [1,2,3]
amount = 11
print(coinChange2(coins,amount))

也就是找到当前节点（即当前面额），然后循环得到该节点减去每个面额硬币后的值，递归该过程，直到面额小于等于0，然后开始回溯。
遍历过程如下：词穷，按红色笔序号的顺序进行的，箭头向下。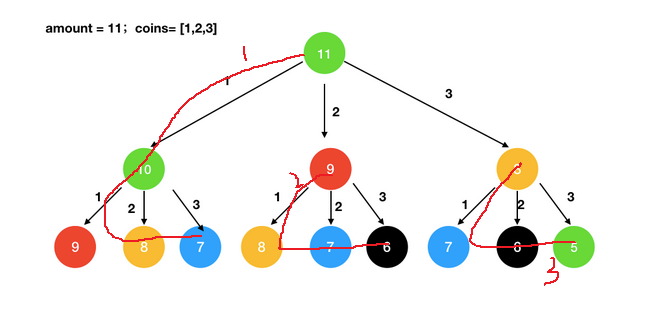

回溯过程：看图中的蓝笔序号吧，语言解释有点词穷，欢迎文笔好的补充，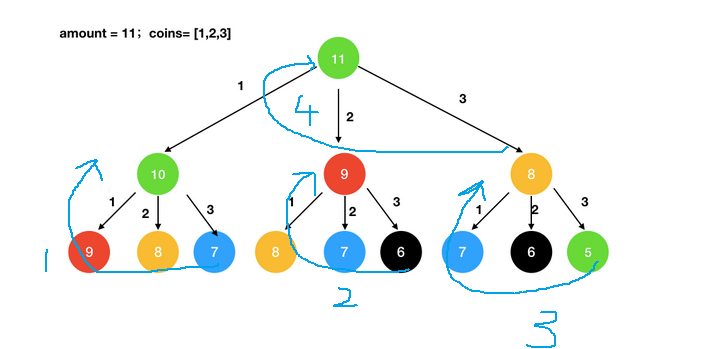

强调一点：这个理解以后这个实现过程中还有很重要的一点，如何记录最优硬币数。首先要明确一个问题，既然是要知道最优硬币数，那这个硬币数肯定是满足条件的，即所有硬币加起来等于我们要求的面额
所以代码实现的时候是不需要保存那些不满足条件的值的，也就是amount<0。那满足的值分为两种情况：第一种是amount>0也就是还没递归完，另一种是amount=0也就是找到了满足条件的解。对应于子节点只有amount<0或者`amount=0`的情况。
if subproblem!=-1:res=min(res,subproblem+1) 根据这一句，在回溯的时候不满足条件的依旧会在后续中一直不满足。而满足条件的则会累加1后与保存的最短节点相比较，进而得出当前金额对应的最优解。
递归算法的时间复杂度分析：子问题总数 x 每个子问题的时间。
子问题总数为递归树节点个数，这个比较难看出来，是 O(n^k)，总之是指数级别的。每个子问题中含有一个 for 循环，复杂度为 O(k)。所以总时间复杂度为 O(k * n^k)，指数级别。
小结一下：这种暴力递归/回溯的方法还是比较容易理解的，先找最后一层的最左结点，然后遍历其所有的兄弟结点，然后对其父亲结点的兄弟结点也做如此的遍历然后一层一层的往上回溯。不漏死角，相比于下面要介绍的第二种做法不知道好理解多少倍。

完全递归

第二种做法的来源是LeetCode官网，说实话也不知道是我心不在焉还是真的智商受到了碾压，我看了一上午愣是没搞懂整个的遍历过程，只看懂了前面的几步，没有总结出规律，所以另辟蹊径写出了上面的递归方法一。后面的学习中我又理解了过程，这种做法是记录下总金额减去0-k个第一种面额的硬币后剩下多少钱，然后将这k种结果中的每一个重复上面的操作，但是这次减去的是第二种面额的硬币，得到的所有结果再减去0-s个第三个面额的硬币，以此类推，计算符合条件的结果。（k，s是当前硬币能满足当前金额的最大值）

%%time
begin=time()
def coinChange3(coins, amount) -> int:
    # 迭代过程
    def digui(idxCoin,coins,amount):
        if amount==0:return 0                              # amount是动态变化的，每一次先看是否到0，也就是找到了满足条件的路径
        minCost=int(1e9)                                    # 定义一个很大的值
        if idxCoin<len(coins) and amount>0:                 # 当不同面额和amount合法时才进行迭代过程
            maxVal=amount//coins[idxCoin]                   # 当前面额相对于当前的amount最大能使用几次
            for i in range(maxVal+1):                       # 从0到最大次数进行遍历
                #if amount>=i*coins[idxCoin]:                # 递归的条件是当前amount大于当前减去的值。我认为不需要。
                print(idxCoin,i,amount-i*coins[idxCoin])    #这是我输出查看结果
                res=digui(idxCoin+1,coins,amount-i*coins[idxCoin])   #针对当前的下标索引，面额，以及amount进行递归
                if res!=-1:minCost=min(minCost,res+i)              #递归结果不等于-1时，更新minCost，也就是最少硬币数
            return minCost if minCost!=int(1e9) else -1               # 最后如果没找到当前的面额没找到满足条件的组合，返回-1
        return -1                                           #运行到这一步，说明不满足上面第二个if的条件，直接返回-1
    return digui(0, coins, amount)                            #递归的开始
coins = [1,2,3]
amount = 11
print(coinChange3(coins,amount))

带备忘录的递归方法

基本数组/字典备忘录

那有了前面斐波那契数列的引入，这里就不在解释什么是备忘录了。我们可以根据上面的图清晰的看到很多结点都是重复计算了，对于金额相同的结点的最优金币数我们可以用一个数组存储起来，当再次访问该金额的时候可以直接调用。
这里可以引申思考一下备忘录的形式，对于本题那肯定是数组比较合适，因为amount的值是从0到11递增的，但是如果是下面的例子呢coins=[186,419,83,408]，amount=6249，显然数组中会有很多值使用不到，造成空间的浪费。此时就可以选择字典来作为存储结构。所以实际应用中要灵活变通，不要拘泥于一种固态思维。

%%time
def coinChange4(coins, amount):
    memo=[int(1e9) for _ in range(amount+1)]
    def dp(amount):
        # 先查找备忘录
        if memo[amount]<int(1e9) :return memo[amount]
        # 初始状态
        if amount==0:return 0
        if amount<0:return -1
        res=int(1e9)                                    
        for i in coins:                   #每个金额都遍历所有的金币
            subproblem=dp(amount-i)       #递归调用
            if subproblem!=-1:
                res=min(res,subproblem+1)            
        memo[amount]=res if res != int(1e9) else -1  #将当前金额的最优解进行存储，以便下次使用
        return memo[amount] 
    return dp(amount)
#coins = [1,2,3]
#amount = 11
coins=[186,419,83,408]
amount=6249
print(coinChange4(coins,amount))

基本思路是不变的，对已经知道最优解的金额存储，下次用到的时候直接调用就好了，也就是对整个递归树进行剪枝。所以核心问题就是如何存，何时取。那肯定是最开始就看看有没有啊，有的话就取出来，没有的话再进行循环，存的时候肯定是找到了当前最优的时候才存啊。
写程序的时候有一点很重要：别想太多。尤其是递归函数部分，你不要去想前一步是什么样，后一步是什么样，只是徒增烦恼。你只要考虑好当前状态，我需要做什么操作，我要返回什么就够了。在调用递归的时候你就认为那是最优的就ok了、比如此题，你确定完起始状态后，只需要盯着当前状态我要做什么操作，你可以认为每个res都是最优的，然后结合当前找出当前最优的结果，那返回肯定返回当前最优的结果或者-1啊。

硬件备忘录

import functools
def coinChange5(coins, amount):
    @functools.lru_cache(amount)              #就这一句话，省了多少事啊
    def dp(rem):
        if rem < 0: return -1
        if rem == 0: return 0
        mini = int(1e9)
        for coin in coins:
            res = dp(rem - coin)
            if res >= 0 and res < mini:
                mini = res + 1
        return mini if mini < int(1e9) else -1
    if amount < 1: return 0
    return dp(amount)
#coins = [1,2,3]
#amount = 11
coins=[186,419,83,408]
amount=6249
print(coinChange5(coins,amount))

看到这个代码的时候，我就只想说：年轻人不讲武德，我劝你好自为之。
这是操作系统/计算机组成原理/计算机体系结构…课程中都会强调的cache转换策略中的LRU算法，后续有时间我会整理一下的，毕竟当时考研也是下了大功夫去学习。

动态规划

那接着上文继续讲，有了斐波那契数列的故事。我们的思路很自然的就过得到如何摆脱递归方法，采用动态规划的方法求解。有了斐波那契数列中自顶向下和自底向上的引入，我们知道动态规划就是如何将上面带备忘录的自顶向上的方法变成利用循环的自底向上的方法。
动态规划三大问：
要想用动态规划求解问题，首先看问题是否满足动态规划使用条件：

• 最优化条件：显然该问题是最优化问题，组成该金额的硬币组合很可能不止一种，我们选最小的，那肯定是最优化问题；
• 无后效性：每个金额的最优解肯定与后面金额无关啊；
• 重叠子问题：金额是叠加来了，那自然满足；

那这样我们就明白了这题满足使用动态规划求解的条件。那该如何使用动态规划求解呢？
根据上一节中求解动态规划问题的一般思路来进行考虑：

• 首先原问题的子问题很明显就能看出来，每个小于我们可以得到的小于求解金额的结点都是它的子问题；
• 接着确定状态：每个结点都是其状态；
• 再接着考虑初始状态：也就是amount=0的情况；
• 最后确定动态转移方程：

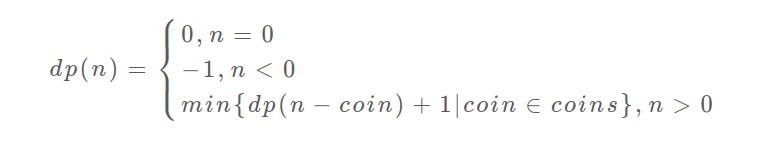
然后根据动态规划三部曲：

• 建立动态转移方程：根据上面的分析我们已经完成了最重要的一步；
• 缓存并复用以往结果：也就是采用备忘录或者DP table来记录节点的值，以方便后续使用；
• 按顺序从小往大算：这一步更像是一条写代码时我们要明确的主线。

  %%time
  def coinChange6(coins, amount):
    memo=[int(1e9) for _ in range(amount+1)]
    memo[0]=0
    for i in range(amount+1):    
        for coin in coins:
            if i<coin:continue
            memo[i]=min(memo[i],memo[i-coin]+1)
    return memo[amount] if (memo[amount] != int(1e9)) else -1
  #coins = [1,2,3]
  #amount = 11
  coins=[186,419,83,408]
  amount=6249
  print(coinChange6(coins,amount))

  很显然，对于自底向上的情况初始状态只有memo[0]=0,然后得到0+coins的值都为1，然后得到0+coins所有的值分别加上coins。那在实现上对于金额i我们就需要判断是当前值小还是i-coins值小。语言是苍白的，灵魂画手上线，看不看得懂随缘。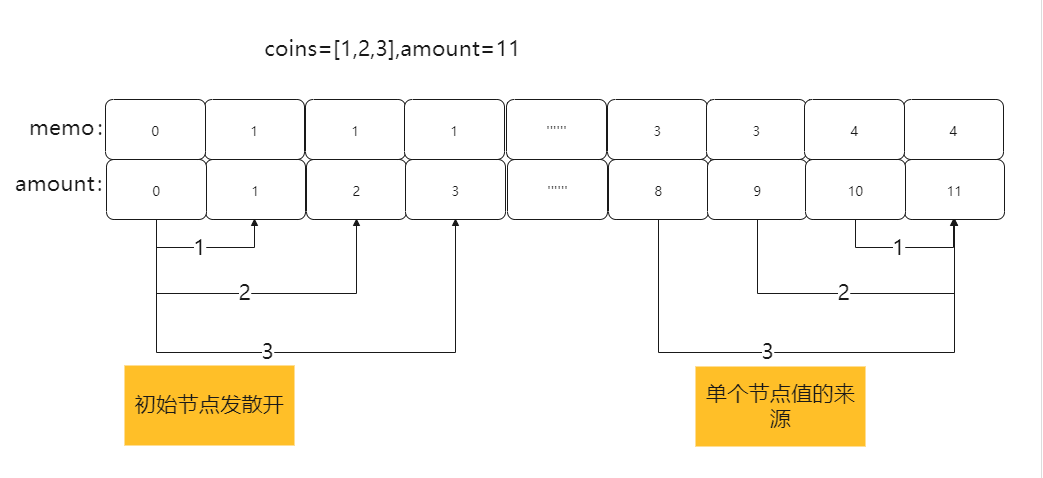
  
  其中要把amount看成是结点的索引值，也就是每个金额对应一个索引。memo是该结点存储的值，也就是当前金额的最优解。每个结点都能发散出三个结点，每个结点（除了初始状态的前几个）也都由三个节点中最小值得到。
  所以对于每个金额都看前三个结点的值中的最小值然后加一，也就是动态转移方程。
  我举的例子有点特别，你们可以想一下硬币数的面额不是连续的情况下是怎样的，比如：coins=[186,419,83,408]，amount=6249。这样我们建立一个数组是不是存在空间上的浪费呢，所以本代码也存在可以空间上优化的地步，当然这只是减少定义无效结点，并不是不保留过往的结点。这并不是状态压缩，这并不是状态压缩，这并不是状态压缩。如何实现的话留给读者自行尝试。
  所以你以为到这就结束了？那十分抱歉，这种做法因为不能进行状态压缩，对于amount很大的情况是非常不友好的，有很多的节点都是无用的但在计算过程中还都一一走了一遍，这就非常耗时间，实验过程中也是如此，在LeetCode平台提交代码的时候动态规划只能超越70%左右的代码，且与前20%差距很大，那这20%是如何实现的呢？

最优解：深度优先搜索DFS+贪心

单纯的凭借DFS是肯定做不到最快的，这里要将DFS与贪心结合，并且疯狂剪枝，最终的效果也好的出奇，代码比较见码云。算法的思想就是优先找面额最大的满足要求的组合，并记录当前路径最小值，那么后续的路径大于最小值的都不在遍历，在小于当中路径最小值的组合中寻找更小的，知道遍历完成。这里面用到了贪心，也就是先找满足最大硬币的组合，但提升速度还是因为这种无底线的剪枝，真香。
时间复杂度不详，但是从实验用例中，快了将近一个数量级。

%%time
def coinChange7( coins, amount):
    def dfs(index, left_amount, count):
        nonlocal ans
        if left_amount == 0:           #当某种硬币组合满足要求时更新路径最小值 
            ans = min(count, ans)   
            return
        if index == len(coins): return    
        k = left_amount // coins[index]   # 当前金额最多满足几个当前的硬币
        while k >= 0 and k + count < ans:   #  前一步循环条件，后一步疯狂剪枝，但凡深度超过了当前的路径最小值
            dfs(index+1, left_amount-k*coins[index], count+k)
            k -= 1
    coins.sort(reverse=True)   ## 先对硬币排序
    ans = 1e10      #既然求最小值，那就先定义一个很大的变量
    dfs(0, amount, 0)    #深度优先搜索入口
    return ans if ans != 1e10 else -1
#coins = [1,2,3]
#amount = 11
coins=[186,419,83,408]
amount=6249
print(coinChange7(coins,amount))