1.算法描述

在n×n格的国际象棋上摆放n个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法。

n皇后是由八皇后问题演变而来的。该问题是国际西洋棋棋手马克斯·贝瑟尔于1848年提出：在8×8格的国际象棋上摆放八个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法。高斯认为有76种方案。1854年在柏林的象棋杂志上不同的作者发表了40种不同的解，后来有人用图论的方法解出92种结果。

2.算法分析

随着计算机的普及和发展，以前人们无法解决的问题，计算机可以简单计算出来。而且思路十分清晰，那就是暴力求解，遍历所有情况，然后计算出解的个数。

2.1 回溯法

按选优条件向前搜索，以达到目标。但当探索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择，这种走不通就退回再走的技术为回溯法

2.2 回溯法思路

用数组模拟棋盘，从第一行开始，依次选择位置，如果当前位置满足条件，则向下选位置，如果不满足条件，那么当前位置后移一位。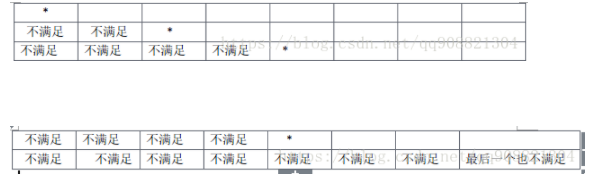

最后一个不满足，回溯到上一行，选下个位置，继续试探。
其实并不需要一个n*n的数组，我们只需要一个n长度的数组来存位置。
表示方式： arr[i] = k; 表示：第i行的第k个位置放一个皇后。这样一个arr[n]的数组就可以表示一个可行解，由于回溯，我们就可以求所有解。

2.3 n皇后回溯求解

因为八皇后不能在同行，同列，同斜线。

每一行放一个皇后，就解决了不在同行的问题。
在第i行的时候，遍历n列，试探位置。和之前所有行放的位置进行比较。
比较列：当前列col 不等于之前所有列。即col != arr[i].
比较斜线，因为不再同一斜率为1或者-1的斜线。(row - i) / (col - arr[i]) != 1 或 -1
可以取巧用绝对值函数: abs(row-i) != abs(col-arr[i])

我们可以提取比较方法：

def judge(t):
    for i in range(1,t+1):
        if x[i]==x[t] or (x[t]-t)==(x[i]-i) or (x[t]+t)==(x[i]+i):
            return False
        return True

2.4 时间复杂度

最坏的情况：每一行有n种情况，有n行，所以时间复杂度为O(n^n)。
但是由于回溯法会提前判断并抛弃一些情况，使得时间复杂度并没有想象中那么高。但是说是O(n!)也不太对，具体怎么算，暂时也不太清楚。（之前想当然了，此处有修正，多谢评论中的提醒。）

2.5 空间复杂度

因为只用了arr[n]的数组，也就是O(n).

PTA上问题

n = int(input())
res = [0 for i in range(n+1)]
vis = [0 for i in range(n+1)]
count = 0
# 若 n = 1，则直接输出结果，若n = 2，循环调用2次f（1），若n = 3，循环调用三次f（2）
# n皇后问题则不需要打印所有，只需要打印复合条件的
def isprint(res):
    global count
    for i in range(1, n+1):
        for j in range(i+1, n+1):
            if res[i] == res[j] or abs(res[i] - res[j]) == abs(i-j):
                return False
    count += 1
    return True
def dfs(t):
    if t == n + 1:
        # res = current_res
        if isprint(res):
            for k in range(1, n+1):
                print(res[k], end=' ')
            print('')
    else:
        for j in range(1, n+1):
            res[t] = j
            if vis[j] == 0:
                vis[j] = 1
                dfs(t+1)
                vis[j] = 0
dfs(1)
print(count, end='')

Algorithm learning

N皇后问题