509 fibonacci-number 斐波那契数列

动态更新bing图片

力扣索引

剑指 Offer 10- I. 斐波那契数列 509. 斐波那契数 Easy

原始问题

The Fibonacci numbers, commonly denoted **F(n)** form a sequence, called the Fibonacci sequence, such that each number is the sum of the two preceding ones, starting from **0** and **1**. That is,
F(0) = 0, F(1) = 1
F(n) = F(n - 1) + F(n - 2), for n > 1.
Given **n**, calculate **F(n)**.
Input: n = 4
Output: 3
Explanation: F(4) = F(3) + F(2) = 2 + 1 = 3.
斐波那契数列（Fibonacci sequence），又称黄金分割数列、因数学家莱昂纳多·斐波那契（Leonardoda Fibonacci）以兔子繁殖为例子而引入，故又称为“兔子数列”，指的是这样一个数列：0、1、1、2、3、5、8、13、21、34、……在数学上，斐波那契数列以如下被以递推的方法定义：F(0)=0，F(1)=1, F(n)=F(n - 1)+F(n - 2)（n ≥ 2，n ∈ N*）。
对于我们而言，可能很多人都在学习递归的时候使用过斐波那契数列作为第一个例子，还有一个是阶乘！

暴力求解—回溯/简单递归

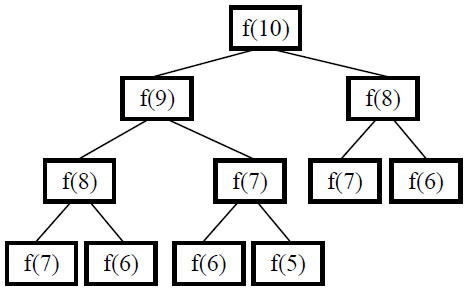
上图，描述了当求F(10)时，系统的运行过程图（部分）。

def fibonacci(n):
    if n<2:
        return n
    else:
        return fibonacci(n-1)+fibonacci(n-2)   # 递归调用
print(fibonacci(10))

根据斐波那契数列的递推公式，代码很好理解。但是递归的开销也是很大的。递归算法造成栈空间的极大浪费，且时间复杂度极高，本代码的时间复杂度为O(2n``)。指数级别的时间复杂度算法跟不能用没啥区别，因为我们要考虑大规模数据的情况，更不必说大数据了。
从上图中，我们可以看出对于F(10)前的结点，我们不止一次的使用到。并且随着树深度的增加，初始结点的调用更是高的可怕。
这只是求fibonacci数列的第十项，如果是第10000，一亿项呢，可能直接就给一般的机器干懵了。所以递归的缺陷尽在不言中。

伪动态规划—带备忘录的递归

为什么说是伪递归呢，那就要理解整个方法的思想以及备忘录的含义。备忘录只是一个形象的说法，我们可以在 暴力求解中看到节点不多，但是节点被计算的次数却随着深度疯狂的扩大。所以很自然的一个想法就诞生了：将我们节点 的值记录下来，当下次要用的时候就可以直接调用了。这样做有什么效果呢，我们画个图来理解一下: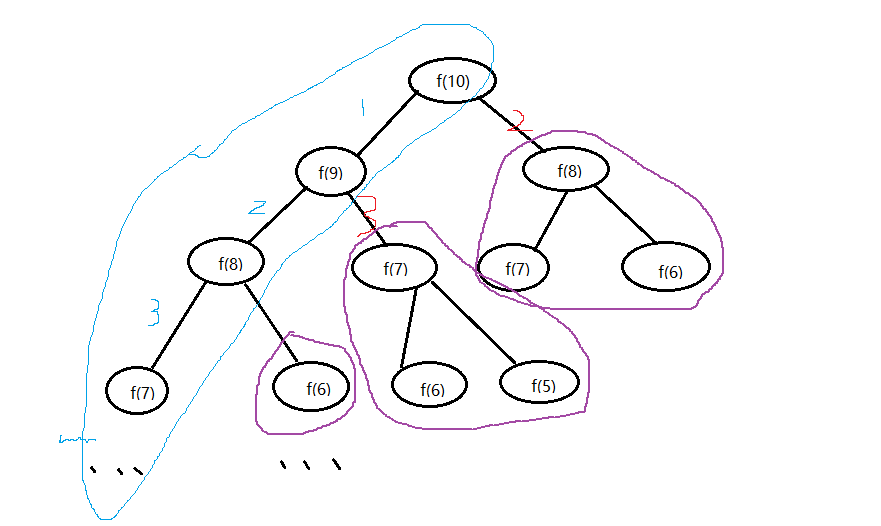

其实对于我们的备忘录递归过程只是走了一遍所有的左节点（蓝色笔圈出部分），当要回溯右边的由于我们的备忘录（数组/字典/…）等结构中已经存储了对应节点的值（对应的数字），也就是说右边的节点（红色笔圈出的地方）是根本就没有访问的。所以什么是带备忘录的递归算法？那不就是把递归算法那棵树进行剪纸操作，减成了一根树条子。（右边节点只需要加上他们根节点对应的值就行，后续节点不用再遍历）。

def fibonacci(n):
    if n<1: return 0
    a=[0 for _ in range(n+1)]  #备忘录初始化为0
    def xxx(a,n):
        print(a,n)
        if (n<3): return 1
        if (a[n] != 0): return a[n]
        a[n] = xxx(a, n - 1) + xxx(a, n - 2)
        return a[n]
    return xxx(a,n)
fibonacci(10)

递归算法的时间复杂度怎么计算？就是用子问题个数乘以解决一个子问题需要的时间。根据上面的图片和代码，我们可以非常非常直观的看出算法的时间复杂度是O(n)。与暴力解法相比，简直不在一个量级上。
到这个地方一部分读者可能又会有一个疑问，既然时间复杂度已经降低到了O(n)，难道还能够再次降低？显然这已经非常好了，将复杂度再次降低基本不可能，毕竟要计算第n项起码要访问一遍前n项，dp数组的时间复杂度也是O(n)，那直接使用这种带备忘录的递归解法不就好了吗，为什么还要提动态规划，dp数组这样高大上的概念了。因为这就涉及到了软件工程中的两种设计模式：自顶向下和自低向上。这是两种完全不一样，甚至相反的思考方法。

那什么是自顶向下呢？ 就是上图中的从我们要求的终止状态f(10)开始，向下求解。简而言之从结果一步步倒推到最简单的起始状态，这种方法就叫自顶向下。所以说递归解法都是自顶向下的。
那什么是自低向上呢？这正是我们下面要讲的dp数组的思考过程，下面会给出思考过程。简而言之从最简单的起始状态一步步的叠加求解出最终我们需要的终止状态，这种方法就叫自低向下。所以dp数组基本上都是脱离了递归，而是采用循环迭代的方式求解。
可能有一部分人忠于循环迭代，对于递归嗤之以鼻，认为递归的方法不但低效且实现过程有点抽象。所以这也一定程度上促进了dp数组的发展。
下面进入正在的正题：dp数组的迭代。这才是真正的动态规划。

动态规划—dp 数组的迭代

那就接着上面的自顶向下和自低向上继续讲，上面由我这位灵魂画手已经很形象的描述了什么是自顶向下， 那么灵魂画手继续上线，解释根据斐波那契数列来解释什么是自底向上：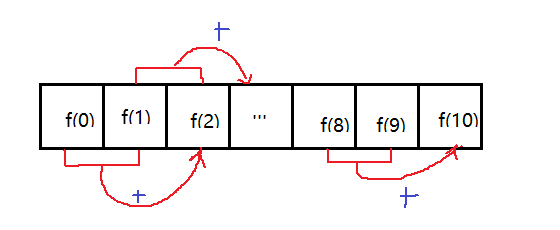

看到红色的线了吗，那就是斐波那契数列自底向上的运动过程啊，先计算最简单的f(0)和f(1)得到f(2)，以此类推，最终由f(8)和f(9)得到f(10)。这个从最简单的起始转移开始迭代到最终的终止状态的过程就叫自底向上。
那么明白了什么是自底向之后，我们需要再去思考以下几个问题，当然有了前面几个问题的铺垫，后面几个问题思考起来是很容易，如果没有前面的铺垫，那看起来估计会很懵，这就是循序渐进。
动态规划三大问：
要想用动态规划求解问题，首先看问题是否满足动态规划使用条件：

• 最优化条件：加法得到唯一值，那肯定是最优的啊；
• 无后效性：当前的解只依赖过去的值；
• 重叠子问题：显然满足；

那这样我们就明白了这题满足使用动态规划求解的条件。那该如何使用动态规划求解呢？
根据上一节中求解动态规划问题的一般思路来进行考虑：

• 首先原问题的子问题很明显就能看出来，每个小于n的节点都是它的子问题；
• 接着确定状态：每个节点都是其状态；
• 再接着考虑初始状态：也就是n=0与n=1的情况；
• 最后确定动态转移方程：本题中动态转移方程也就是它的递归式；

然后根据动态规划三部曲：

• 建立动态转移方程：我们已经完成了最重要的一步，其实就是递推式嘛。

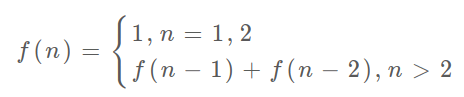
• 缓存并复用以往结果：也就是采用备忘录或者DP table来记录节点的值，以方便后续使用。
• 按顺序从小往大算：这一步更像是一条写代码时我们要明确的主线。

具体代码如下：

def fibonacci(n):
    # 这是三部曲第二步：就是建立一个缓存数组或者字典等存储结果以便复用
    temp = list(range(n+1)) # 创建一个定长的数组，用来存放对于结点F(x)的值
    # 这是三部曲第三步：明确初始状态后从小往大算
    for i in range(n+1):   # 从初始状态开始计算
        if i < 2:
            temp[i] = i
        else:                  # 这是三部曲第一步状态转移方程
            temp[i] = temp[i-1] + temp[i-2]
    return temp[-1]
result = fibonacci(10) 
print(result)

状态压缩

多说一句：本题中我们不需要知道前n-3个状态的值，我们只需要知道n-1与n-2状态的值就能够求解。所以本题可以不保存前面的值，那这样算法的空间复杂度就降到了O(1).

def fibonacci(n):
    pro,end=0,1     # 数字间是有关系的，可以理解成两个指针。但他们对应的是具体的值。
    for i in range(2,n+1):  
        pro,end=end,pro+end
    return end
result = fibonacci(10) 
print(result)

这个技巧被称为状态压缩，也就是只记录必要的值，以减少dp数组/dp表的大小。

总结

之所以动态规划，动态转移方程都加上动态二字，从递推式我们可以看出动态的意思，就是将该问题通过状态方程实时的转移到子问题，一直转到最开始，最基础的问题上。现在明白什么是动态规划，什么是动态转移方程了吗？更浅显的描述就是把大问题不断的进行拆分成一个个不独立（不能叫相互关联，因为只是部分关联）的子问题，然后由自顶向下和自低向上两种方式就得到了带备忘录的递归解法和dp数组解法。
In my opinion，暴力递归，备忘录递归以及dp数组这三种方式都可以称之为动态规划，因为它们在实现过程中核心思想都是将自己的状态转移到更小的子问题上，只是思想中添加了一些技巧。但是往往还是称自底向上的方法为动态规划法。
可以看出三种方法都是围绕着一个核心，也就递推式/状态转移方程。一旦有了状态转移方程，那就很容易去求解了。后面只是如何将算法进行优化的问题了。这个题只是一个入门题，并没有真正体现出动态规划的意义。但是起码让我们扫清了一些迷雾。后面的例子

补录：

原本我以为上面的四种方法已经完完全全讲透了斐波那契数列的求解。然而还是我见识浅薄了啊、

第五种解：矩阵求幂

看一下斐波那契数列的矩阵方程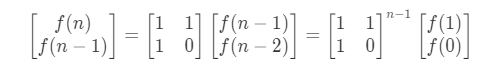

看到这个方程你想说什么，真的是点子很多啊，将矩阵结合进来。其实本质是不变的，但是可以通过求矩阵的方式解决问题。下面给出抄袭的代码，感兴趣的可以试一下，看不懂的也没关系，把上面的看明白就行，这里仅作为一个扩展。

class Solution:
    def fib(self, N: int) -> int:
        if (N <= 1):
            return N
        A = [[1, 1], [1, 0]]
        self.matrix_power(A, N-1)
        return A[0][0]
    def matrix_power(self, A: list, N: int):
        if (N <= 1):
            return A
        self.matrix_power(A, N//2)
        self.multiply(A, A)
        B = [[1, 1], [1, 0]]
        if (N%2 != 0):
            self.multiply(A, B)
    def multiply(self, A: list, B: list):
        x = A[0][0] * B[0][0] + A[0][1] * B[1][0]
        y = A[0][0] * B[0][1] + A[0][1] * B[1][1]
        z = A[1][0] * B[0][0] + A[1][1] * B[1][0]
        w = A[1][0] * B[0][1] + A[1][1] * B[1][1]
        A[0][0] = x
        A[0][1] = y
        A[1][0] = z
        A[1][1] = w

你认为这就完了，那你可能跟我一样太天真了啊，斐波那契数列不但可以结合矩阵求解，尽然还能结合黄金分割比求解。

第六种解：公式法

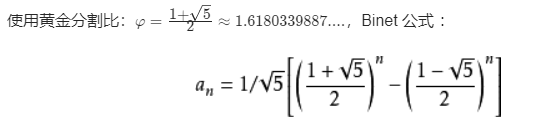
想深入了解二者之间关系的，下面给出一个链接：广义斐波那契数列和黄金比例
这样就能在常数的空间和时间复杂度求解问题。
玄学啊。。。。

# Contributed by LeetCode user mereck.
class Solution:
  def fib(self, N):
      golden_ratio = (1 + 5 ** 0.5) / 2
      return int((golden_ratio ** N + 1) / 5 ** 0.5)

这次我相信应该是写完了斐波那契数列。