518 coin-change-2 零钱兑换 II - 图1
动态更新bing图片

力扣索引

518. 零钱兑换 II Medium

原始问题

You are given coins of different denominations and a total amount of money. Write a function to compute the number of combinations that make up that amount. You may assume that you have infinite number of each kind of coin.
给定不同面额的硬币和一个总金额。写出函数来计算可以凑成总金额的硬币组合数。假设每一种面额的硬币有无限个。
Input: amount = 5, coins = [1, 2, 5]
Output: 4
Explanation: there are four ways to make up the amount:
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1
图例（如果有的话），引入

两种错误的暴力求解思考

在思考暴力求解的时候我们自然而然想到的是循环解决。有n个硬币就有n层循环，这样就会得到n个硬币的组合，判断一下这些硬币加起来与amount的关系，已达到暴力求解，但是这种方法是错误的，因为我们不知道要做多少层的循环，伪代码如下：

  1. for i in range(amount//coin1+1):
  2.     for j in range(amount//coin2+1):
  3.         for k in range(amount//coin3+1):
  4.             ....
  5.                 i*coin1+j*coin2+k*coin3....amount   #判断二者关系

第二种错误的思路是通过当前金额每次减掉每个硬币数，然后累加结果得0的情况，这样会重复计算，代码如下

  1. def coinChangeTwo(coins,amount):
  2.     ans=0
  3.     def digui(amount):
  4.         nonlocal ans
  5.         if amount==0:ans+=1
  6.         if amount>0:
  7.             for coin in coins:
  8.                 digui(amount-coin)
  9.     digui(amount)    
  10.     return ans
  11. coins=[1,2,5]
  12. amount=5
  13. print(coinChangeTwo(coins,amount))

如上图（点上面流程图的缩放比例数字，然后选择适应画布，可以自动调整好大小）。找到的节点中包含了重复的组成部分，重复计算了122,221等情况，所以这种解法也有问题。
我一直认为去学习正确的方法收效甚微，你只是理解了别人的做法，但是你并没有融会贯通。学习错误的做法，才知道哪些是坑，哪些路线不能走，结合自己的思考才能真正的理解其中所蕴含的内容，才会明天那些正确解是如何得到的，才能有所顿悟。上面都是我对这题的考虑过程，到现在为止我也只是半会半不会，但我认为记下这些过程在以后复盘的时候是有益处的。

暴力匹配

完全递归

那就要换个想法了，第一想法是记录走过的路然后排重。但是这样实现起来就很麻烦。用硬币去累加出金额的做法行不通，是因为相同数量的硬币出现重复的情况，那如何避免硬币不重复呢，再想想上面第一种错误，我们先求每个面额满足的硬币数看起来是可行的。故换个想法，记录下总金额减去0-k个第一种面额的硬币后剩下多少钱，然后将这k种结果中的每一个重复上面的操作，但是这次减去的是第二种面额的硬币，得到的所有结果再减去0-s个第三个面额的硬币，以此类推。（k，s是当前硬币能满足当前金额的最大值）。过程图我就不画了，看上面的描述自行脑补吧。补一个简单例子的过程图吧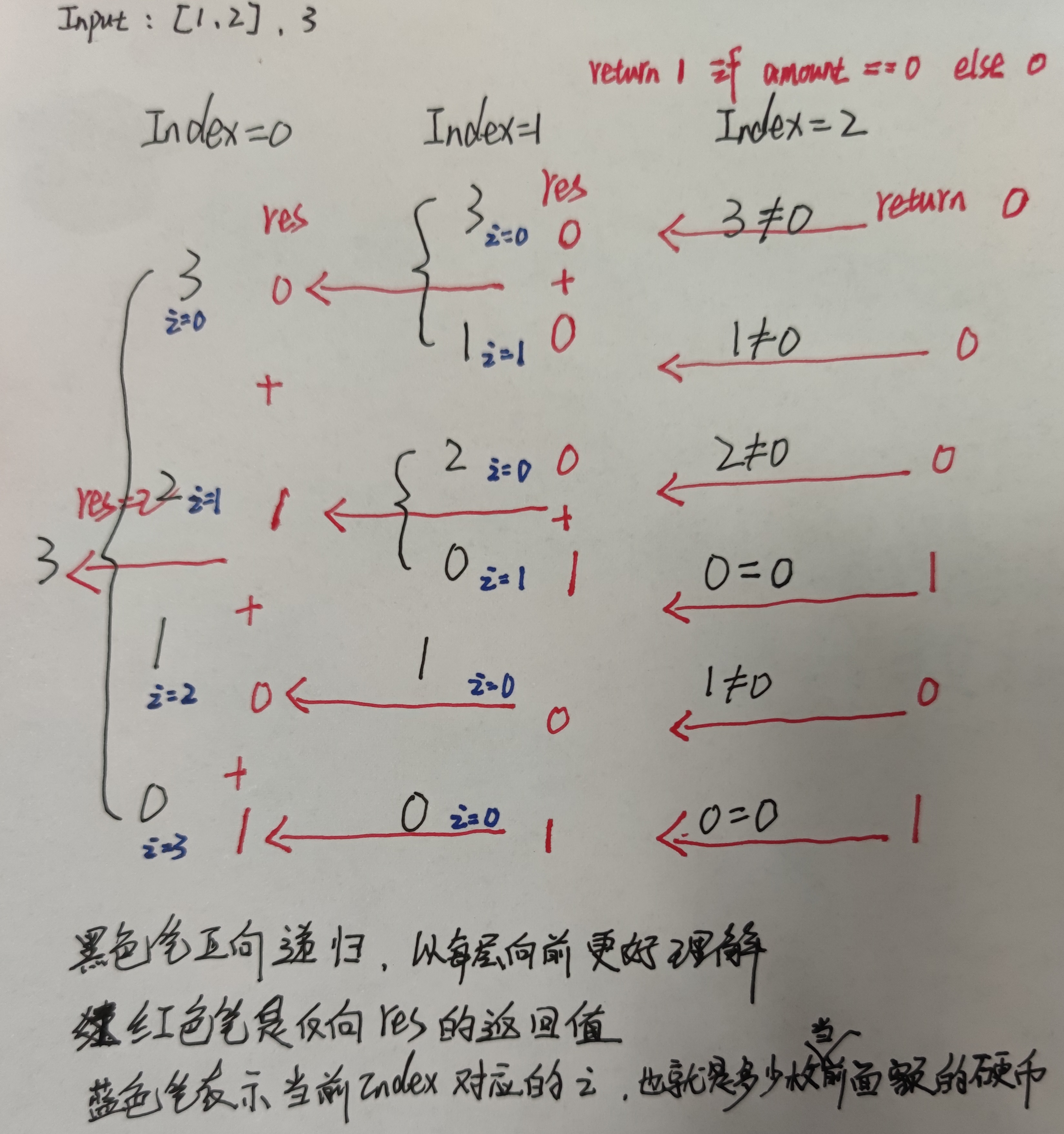
IMG_20210110_151553.jpg

  1. def coinChangeTwo2(coins,amount):
  2.     def digui(index,amount):
  3.         if index == len(coins): return 1 if amount == 0 else 0
  4.         i,res=0,0
  5.         while amount>=i*coins[index]:
  6.             res+=digui(index+1,amount-i*coins[index])
  7.             i+=1
  8.         return res
  10.     return digui(0,amount) 
  11. coins=[1,2,5]
  12. amount=5
  13. print(coinChangeTwo2(coins,amount))

最基本的递归解法，好好看看也是最容易理解的。时间复杂度高的可怕。

518 coin-change-2 零钱兑换 II - 图3

深度优先搜索DFS

同518 coin-change-2 零钱兑换 II问题一样，深度优先搜索也是一种可供思考求解的方法。

  1. %%time
  2. def coinChangeTwo3(coins,amount):
  3.     ans=0
  5.     def dfs(index,amount):   ##核心部分
  6.         nonlocal ans
  7.         if amount==0: ans+=1
  8.         if amount<0 or index==len(coins): return  
  9.         while index<len(coins):
  10.             dfs(index,amount-coins[index])
  11.             index+=1
  12.     dfs(0,amount)
  13.     return  ans
  16. coins=[1,2,5]
  17. amount=5
  18. print(coinChangeTwo3(coins,amount))

看看跟我们上面第二种错误方法区别在哪，只是修改了一部分，可以这样说是将以金额为中心的递归转化成了以硬币为中心的深度优先搜索，树的构造都不一样了。下图中填充颜色的是 DFS 访问过的结点，还有一部分 amount<0 的结点未标记出。 可见其实 DFS 是对整个树进行了一种剪枝，这种剪枝的手法真的是点到为止。

518 coin-change-2 零钱兑换 II - 图4 时间复杂度一般是到不了这么高的，可能只有1/2左右吧，这个还真要视情况而定。

带备忘录的递归方法

由322 coin-change 零钱兑换和509 fibonacci-number 斐波那契数列的基础，我们很自然的就能够过渡到对于那些重复计算的结点进行一些操作，也就是在第一次计算的时候保存下结点的值，以便下次调用的时候能够直接使用而提高算法整体的性能。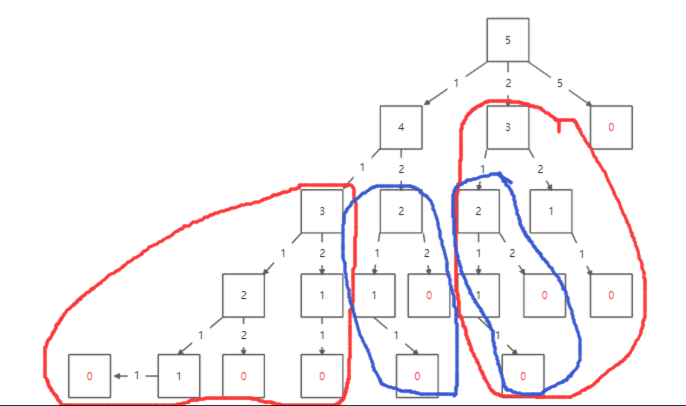
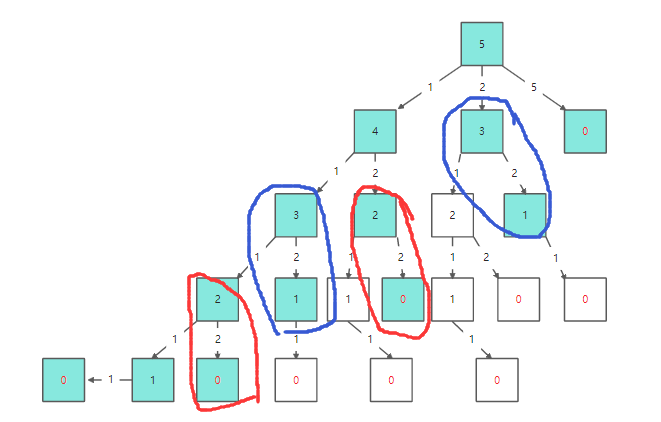
image.pngimage.png
可以看出上面两幅图中不同颜色圈出来的地方都是冗余的，上面图中只是举例子说明很多结点需要重复计算，其实具体树的构造是类似于上面那种手写图。当随着树深度的叠加，需要重复计算的结点会成指数级别的出现。所以对于给递归添加一个备忘录，利用增加一点有限的空间换取一个高优化时间复杂度是非常可行的。
那问题就来了，当动手开始写的时候发现理论很靠谱，实际操作无从下手。322 coin-change 零钱兑换中实现记忆化（备忘录）的方法好像在这里根本就行不通，所以说哪怕是一个场景的问题换个问法，那可能就是天差地别，模板并不是万能的，还是要具体问题具体分析。
再次仔细思考，虽然不能够直接利用结点中金额进行一个备忘录查找，但是我们可以结合边，形成一种以边+结点来进行记忆化操作。也就是从每个硬币到该金额都是一样的话那后续就不用再计算了。因为我们再做递归的时候是每层递归一个硬币，如果后续高额的硬币被提前用了，那后续再次调用的时候是可以用的，但是后续是不能再回去使用前面用到过的面额硬币的。我自己都说蒙了，看代码吧，跟上面的比较比较看看差异在哪。

  1. %%time
  2. def coinChangeTwo4(coins,amount):
  3.     memo={}
  4.     def digui(index,amount):
  5.         if (str(index)+','+str(amount)) in memo.keys():return memo[str(index)+','+str(amount)]
  6.         if index == len(coins): return 1 if amount == 0 else 0
  7.         i,res=0,0
  8.         while amount>=i*coins[index]:
  9.             res+=digui(index+1,amount-i*coins[index])
  10.             i+=1
  11.         memo[str(index)+','+str(amount)]=res
  12.         #print(memo)
  13.         return res
  15.     return digui(0,amount) 
  18. coins=[1,2,5]
  19. amount=5
  20. print(coinChangeTwo4(coins,amount))

时间复杂度那肯定是再次被降低，具体不详。实验用例很小，且使用了字典才导致跟上一个代码差不多，当随着树深度的增加，才会显示出这种做法是比单纯的DFS/递归更优秀的。

动态规划

由前面我们知道带备忘录的递归是自顶向下，而动态规划是自底向上。那就要思考如何才能倒着实现呢？
动态规划三大问：
要想用动态规划求解问题，首先看问题是否满足动态规划使用条件：

  • 最优化条件：显然这题不是最优化问题，但我我们是通过零钱兑换中的最优化问题来变相求解该问题，所以可以勉强看成符合条件。
  • 无后效性：每个金额的最优解肯定与后面金额无关啊；
  • 重叠子问题：金额是叠加来了，那自然满足；

那这样我们就明白了这题满足使用动态规划求解的条件。那该如何使用动态规划求解呢？
根据上一节中求解动态规划问题的一般思路来进行考虑：

  • 首先原问题的子问题很明显就能看出来，每个小于我们可以得到的小于求解金额的结点都是它的子问题；
  • 接着确定状态：每个结点都是其状态；
  • 再接着考虑初始状态：也就是amount=0的情况以及最后一枚硬币能否被整除；
  • 最后确定动态转移方程：

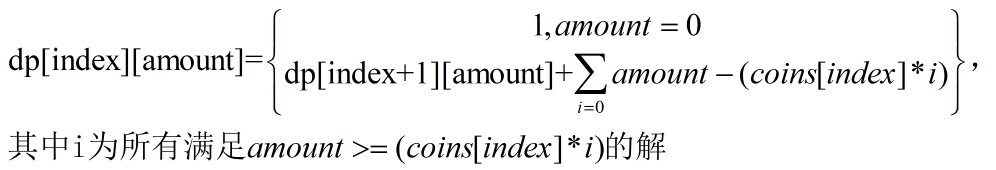
image.png

然后根据动态规划三部曲：

  • 建立动态转移方程：根据上面的分析我们已经完成了最重要的一步；
  • 缓存并复用以往结果：就是采用DP table来记录节点的值，以方便后续使用；
  • 按顺序从小往大算：这一步更像是一条写代码时我们要明确的主线。

有一点，上面的带备忘录的递归其实也应该使用我手写图这种树结构来分析，但是我手写的例子太少了，动态规划也是用手写图这种树结构来分析。
IMG_20210110_151553.jpg
可以说很明显红色笔的过程就是我们动态规划考虑的过程，只是我们要补全所有情况。
因为当前金额有几种组成方案是有index和amount共同得到的，故采用二维表格作为缓存
首先，根据前面讲的，我先来画个图说明一下动态转移方程的整个过程。然后再去看代码就很清晰的理解了。
还记得前面说的带备忘录的递归和动态规划的区别吗？自顶向下和自底向上。没错我又提了一遍，因为这点不理解后面是想不明白的，上面说了是红色笔的过程。那我们先考虑动态规划最初始的状态，首先的自底向上，那是不是amount=0的时候，既然是这个时候，那最后一枚硬币要满足什么要求呢，0枚，1枚到n枚，可能是小数吗，不可能。 既然是这样，那金额满足什么情况呢，肯定整数倍啊，对于下表的解读也就是0枚面额5的硬币和1枚面额为5的硬币。
所以我们可以填充下面表格的最后一行：

index/amount 0 1 2 3 4 5
1(coins[0]=1)
2(coins[1]=2)
5(coins[2]=5) 1 0 0 0 0 1

到这一步是没有问题的，我们继续思考，因为是自底向上吗，所以我们该考虑倒数第二行。dp[1][j]如何求呢，那肯定是在最后一层给定硬币的基础上加上当前硬币才能够构造出对应的面额啊。 那也就是j=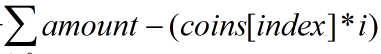image.png,将符合要求的累加就得到了所有满足的条件。比如对于index=2，amount=5这个元素，如何来计算呢，首先是找index=3，amount=5-2*0;index=3，amount=5-2*1;index=3,amount=5-2*2这三个元素的值然后累加作为在这两枚硬币情况下不同的组合情况。每个元素都这样计算，也就对应着每个面额当前这些硬币所满足的所有组合数。

index/amount 0 1 2 3 4 5
1(coins[0]=1)
2(coins[1]=2) 1 0 1 0 1 1
5(coins[2]=5) 1 0 0 0 0 1

按照上面的思想，我们填完第一行。index=2，amount=5-1*0;
index=2，amount=5-1*1;
index=2，amount=5-1*2;
index=2，amount=5-1*3;
index=2，amount=5-1*4;
index=2，amount=5-1*5;
累加这些元素，因为他们都是对应不同枚面额为1的硬币组成的，肯定不会重复。同时也列举了所有情况，所以也是最优解。

index/amount 0 1 2 3 4 5
1(coins[0]=1) 1 1 2 2 3 4
2(coins[1]=2) 1 0 1 0 1 1
5(coins[2]=5) 1 0 0 0 0 1

没品明白的，你仔细品，再品不懂，你就品品代码，然后再回头品。代码如下：

  1. %%time
  2. def coinChangeTwo5(coins,amount):
  3.     if amount==0 : return 1
  4.     if len(coins)==0:return 0
  5.     n=len(coins)
  6.     dp=[[0 for i in range(amount+1)] for i in range(n)]  #定义table表
  7.     for i in range(amount+1):          #初始化最后一行，
  8.         if i%coins[-1]==0 : dp[-1][i]=1
  9.     i=n-2
  10.     while i>=0:                       #从后一行往上遍历每一行
  11.         for j in range(amount+1):     #每一行从头到尾填表
  12.             dp[i][j]=dp[i+1][j]        # 先复制上一行的值， 就是将硬币为0的情况单独先计算了
  13.             k=j-coins[i]         
  14.             while k>=0:               # 然后累加符合要求的面额的组合数
  15.                 dp[i][j]+=dp[i+1][k]   
  16.                 k-=coins[i]
  17.         i-=1
  18.     return dp[0][amount]
  21. coins=[1,2,5]
  22. amount=5
  23. print(coinChangeTwo5(coins,amount))

写了很久，尽力的描述清楚了，讲了很多废话。时间复杂度就是填表的过程乘上while循环。
image.png
这是最坏的情况，也就是硬币面额从1开始递增才会这样，我认为是O(n``*(amount+1)``)
空间复杂度就是建表的空间：O(n*(amount+1))

初步优化

上诉的动态优化过程实则还可以进一步的优化，那哪个地方可以 优化呢？ while循环
对于每一行来说再计算index=i，amount=j的时候要累加index=i+1，amount=j-coins[i]*k的所有位置，但是从从(i+1,0)到(i+1, j - coins[i])这些已经被(i, j - coins[i])计算过了，所以可以做修改。用大白话来说就是计算index=2，amount=4的时候可以借助index=2，amount=2的值，这样就不用再去遍历index=3中的元素了，因为index=2，amount=2已经帮我们计算过了。

  1. %%time
  2. def coinChangeTwo5(coins,amount):
  3.     if amount==0 : return 1
  4.     if len(coins)==0:return 0
  5.     n=len(coins)
  6.     dp=[[0 for i in range(amount+1)] for i in range(n)]  #定义table表
  7.     for i in range(amount+1):          #初始化最后一行，
  8.         if i%coins[-1]==0 : dp[-1][i]=1
  9.     i=n-2
  10.     while i>=0:                       #从后一行往上遍历每一行
  11.         for j in range(amount+1):     #每一行从头到尾填表
  12.             dp[i][j]=dp[i+1][j]        # 先复制上一行的值， 就是将硬币为0的情况单独先计算了
  13.             dp[i][j]+=dp[i][j-coins[i]] if j-coins[i]>=0 else 0    
  14.             # 加的是本行的j-coins[i] 的值，因为一枚硬币的情况知道了，那两枚硬币的情况是一样的，不会变
  15.         i-=1
  16.     return dp[0][amount]
  19. coins=[1,2,5]
  20. amount=5
  21. print(coinChangeTwo5(coins,amount))

能这样优化的原因就是，对于同样面额的硬币（同一行），我知道比我少一枚的金额有多少种组成方案，那加上这枚硬币后的金额组成情况是与它相同的。再加上没有这枚硬币组成当前面额的情况，所有可能就全部列举出来了。 也就是对于当前面额的硬币和当前的金额，我只需要知道0枚当前面额硬币组成当前金额和当前金额减去一枚当前面额的硬币后该金额的组成情况。
时间复杂度：O(n*(amount+1))
空间复杂度就是建表的空间：O(n*(amount+1))

状态压缩

那时间复杂度优化后，能优化空间吗？回过头看一下动态规划和优化的情况，每个index=i，amount=j我们是先做了一遍复制index=i+1，amount=j的操作，然后加上index=i,amount=j-coins[i]。那这样我们之间在一行上操作不就好了嘛，那这样空间就变成了线性的。

  1. %%time
  2. def coinChangeTwo7(coins,amount):
  3.     if amount==0 : return 1
  4.     dp=[0 for i in range(amount+1)]
  5.     for j in range(amount+1):          #初始化最后一行，
  6.         if j%coins[-1]==0 : dp[j]=1
  7.     i=len(coins)-2        
  8.     while i>=0:                       #从后一行往上遍历每一行
  9.         for j in range(amount+1):     #每一行从头到尾填表
  10.             dp[j]+=dp[j-coins[i]] if j-coins[i]>=0 else 0    # 加的是本行的j-coins[i] 的值，因为一枚硬币的情况知道了，那两枚硬币的情况是一样的，不会变
  11.         i-=1
  12.     return dp[amount]
  15. coins=[1,2,5]
  16. amount=5
  17. print(coinChangeTwo7(coins,amount))

时间复杂度：O(n*(amount+1))。空间复杂度就是建表的空间：O(amount+1)

状态压缩再优化

但是我们仍然不满足，因为代码还能进一步优化。为什么要把最后一排单独拿出来计算呢，最后一排的规律也跟其余一样啊，我们只需要初始化dp[0]就可以了。

  1. %%time
  2. def coinChangeTwo7(coins,amount):
  3.     dp=[1]+[0 for i in range(amount)]
  4.     for coin in coins:                       #从后一行往上遍历每一行
  5.         for j in range(amount+1):     #每一行从头到尾填表
  6.             dp[j]+=dp[j-coin] if j-coin>=0 else 0    # 加的是本行的j-coins[i] 的值，因为一枚硬币的情况知道了，那两枚硬币的情况是一样的，不会变
  7.     return dp[amount]
  10. coins=[1,2,5]
  11. amount=5
  12. print(coinChangeTwo7(coins,amount))

代码还是有点啰嗦，为了保证j-coin我们之间从coin开始循环就行了，然后去掉统计时间的代码，最后得到最简洁的版本。
时间复杂度：O(n*(amount+1))。空间复杂度就是建表的空间：O(amount+1)

  1. %%time
  2. def coinChangeTwo7(coins,amount):
  3.     dp=[1]+[0]*amount
  5.     for coin in coins:
  6.         for i in range(coin,amount+1):
  7.             dp[i] +=dp[i-coin]
  8.     return dp[-1]
  11. coins=[1,2,5]
  12. amount=5
  13. print(coinChangeTwo7(coins,amount))

就这短短的三五行代码，解决了这样一个问题。前面可是费了很大的功夫啊。而且时间和空间的开销都还很好。
时间复杂度：O(n*(amount+1))。空间复杂度就是建表的空间：O(amount+1)。当时时间消化肯定是要少的。

最终：dp+剪枝

你要是跟我一样以为这就完了，那我们真的是一样天真。看见标题也就知道了，上面的代码还能够再次优化，（不讲武德）。上面说的那么详细了，最后的剪枝就自己领略吧。上面没看懂，这个地方也不必看。

  1. def coinChangeTwo10(coins,amount):
  2.     if not amount:return 1
  3.     coins.sort(reverse = True)
  4.     dp = [0] * (amount + 1)
  5.     for coin in coins:
  6.         if coin > amount:continue
  7.         dp[coin] += 1
  8.         for i in range(coin, amount - coin +1):
  9.             dp[i + coin] += dp[i]
  10.     return dp[amount]
  12. coins=[1,2,5]
  13. amount=5
  14. print(coinChangeTwo10(coins,amount))

这个代码0的时间消耗在力扣上是最低了，也就是超越了100%。时间复杂度肯定大大低于O(n*(amount+1))。空间复杂度不变O(amount+1)。

写到这我差不多，两天时间完完全全的把这题给搞清楚，从头到尾记录解题过程。虽然耗时良久，但是很值得啊。