0x18 总结与练习

括号画家

达达是一名漫画家，她有一个奇特的爱好，就是在纸上画括号。
这一天，刚刚起床的达达画了一排括号序列，其中包含小括号 ( )、中括号 [ ] 和大括号 { }，总长度为 。
这排随意绘制的括号序列显得杂乱无章，于是达达定义了什么样的括号序列是美观的：

1. 空的括号序列是美观的；
2. 若括号序列 是美观的，则括号序列 #card=math&code=%28A%29&id=K0sf9)、、 也是美观的；
3. 若括号序列 都是美观的，则括号序列 也是美观的。

例如 (){} 是美观的括号序列，而)({)[}]( 则不是。
现在达达想在她绘制的括号序列中，找出其中连续的一段，满足这段子串是美观的，并且长度尽量大。
你能帮帮她吗？

输入格式
输入一行由括号组成的字符串。
输出格式
输出一个整数，表示最长的美观的子段的长度。
数据范围
字符串长度不超过 。
输入样例：

({({(({()}})}{())})})[){{{([)()((()]]}])[{)]}{[}{)

输出样例：

4

栈 + 动态规划
表示以 i 为结尾，最长的美观括号序列长度。
当我们使用栈去给每个右括号匹配左括号时，可以知道左括号的位置，然后顺便做转移即可。
栈里面需要保存括号类型以及对应的下标，也可以只保存下标，但编码会稍复杂一点。

#include <bits/stdc++.h>
using namespace std;
const int N = 100010;
char s[N];
int st[N],top,d[N];
int id[200];
int main(){
    scanf("%s",s+1);
    int n = strlen(s+1);
    int res = 0;
    id['('] = -1;id[')'] = 1;
    id['['] = -2;id[']'] = 2;
    id['{'] = -3;id['}'] = 3;
    for(int i=1;i<=n;i++){
        if(id[s[i]] < 0){
            st[++top] = i;
        }else{
            if(top == 0 || id[s[st[top]]] + id[s[i]] != 0){
                top = 0; continue;
            }else{
                d[i] = i - st[top] + 1;
                top--;
            }
        }
    }
    for(int i=1;i<=n;i++){
        d[i] += d[i-d[i]];
        res = max(d[i],res);
    }
    cout << res << endl;
    return 0;
}

表达式计算4

给出一个表达式,其中运算符仅包含+,-,,/,^（加 减 乘 整除 乘方）要求求出表达式的最终值。数据可能会出现括号情况，还有可能出现多余括号情况。数据保证不会出现大于或等于的答案。数据可能会出现负数情况。
输入格式
输入仅一行，即为表达式。
输出格式
输出仅一行，既为表达式算出的结果。
*输入样例：

(2+2)^(1+1)

输出样例：

16

本题难度较大，主要是坑点多。

回顾：表达式计算的通常思路是将中缀表达式转换为后缀表达式，每次当运算符入栈时，如果栈顶运算符的优先级比当前运算符的优先级要大，那么我们会优先计算栈顶运算符，直到该条件不被满足。

本题中，运算符优先级由高到低依次是：^，*，/，+，-
另外特殊情况是：

1. 多余括号，容易想到多余的左括号其实不需要被管理，那么多余的右括号呢？为了方便处理，我们再表达式开头补充若干个左括号即可。
2. 存在负数，即 3 + -2其中的 -2 的 - 号前面是一个运算符，因此该处的 - 需要被认为是一个负数。另外，如果减号后面是一个左括号，那么这时我们只需要将该操作变为 -1 * 即可，方便统一处理。
3. 开头如果出现负号，比如 -2^2，需要将其改为 0-2^2，因为此处的负号不能简单的与后面的内容合并为一个负数整体。

#include <bits/stdc++.h>
using namespace std;
string s;
stack<int> nums;
stack<int> ops;
int power(int a, int b) {
    int rs = 1;
    for(;b;b>>=1) {
        if(b & 1) rs *= a;
        a = a * a;
    }
    return rs;
}
void calc() {
    int a = nums.top(); nums.pop();
    int b = nums.top(); nums.pop();
    char c = ops.top(); ops.pop();
    int d = 0;
    if(c == '+') d = a + b;
    else if(c == '-') d = b - a;
    else if(c == '*') d = a * b;
    else if(c == '/') d = b / a;
    else d = power(b, a);
    nums.push(d);
}
int main(){
    cin >> s;
    if(s[0] == '-') s = '0' + s;
    int cnt = 0;
    for(auto &c : s) {
        if(c == '(') cnt --;
        else if(c == ')') cnt ++;
    }
    if(cnt > 0) s = string(cnt, '(') + s;
    s = '(' + s + ')';
    for(int i = 0; i < s.size(); i++) {
        if(s[i] >= '0' && s[i] <= '9') {
            int j = i, x = 0;
            while(isdigit(s[j])) {
                x = x * 10 + s[j] - '0';
                j ++;
            }
            nums.push(x);
            i = j - 1;
        } else {
            auto c = s[i];
            if(c == '(') ops.push(c);
            else if(c == ')') {
                while(ops.top() != '(') calc();
                ops.pop();
            } else if(c == '^') {
                while(ops.top() == '^') calc();
                ops.push(c);
            } else if(c == '*' || c == '/') {
                while(ops.top() == '/' || ops.top() == '*' || ops.top() == '^') calc();
                ops.push(c);
            } else if(c == '+' || c == '-') {
                if(c == '-' && !isdigit(s[i - 1]) && s[i - 1] != ')') {
                    // 此处的减号表示后面是一个负数
                    if(s[i + 1] == '(') {
                        nums.push(-1);
                        ops.push('*');
                    } else {
                        int j = i + 1,  x = 0;
                        while(isdigit(s[j])) {
                            x = x * 10 + s[j] - '0';
                            j ++;
                        }
                        nums.push(-x);
                        i = j - 1;
                    }
                } else {
                    // 由于所有运算符优先级都大于等于加号和等号，所以直接运算到左括号
                    while(ops.top() != '(') calc();
                    ops.push(c);
                }
            }
        }
    }
    cout << nums.top() << endl;
    return 0;
}

城市游戏

有一天，小猫 rainbow 和 freda 来到了湘西张家界的天门山玉蟾宫，玉蟾宫宫主蓝兔盛情地款待了它们，并赐予它们一片土地。这片土地被分成 个格子，每个格子里写着 R 或者 F，R 代表这块土地被赐予了 rainbow，F 代表这块土地被赐予了 freda。现在 freda 要在这里卖萌。。。它要找一块矩形土地，要求这片土地都标着 F 并且面积最大。但是 rainbow 和 freda 的 OI 水平都弱爆了，找不出这块土地，而蓝兔也想看 freda 卖萌（她显然是不会编程的……），所以它们决定，如果你找到的土地面积为 ，它们将给你 两银子。
输入格式
第一行包括两个整数 ，表示矩形土地有 行 列。接下来 行，每行 个用空格隔开的字符 F 或 R，描述了矩形土地。每行末尾没有多余空格。
输出格式
输出一个整数，表示你能得到多少银子，即(最大 F 矩形土地面积)的值。
数据范围

输入样例：

5 6
R F F F F F
F F F F F F
R R R F F F
F F F F F F
F F F F F F

输出样例：

45

该题目可以转换为：
给定一个 01 矩阵，求最大的全1矩阵面积。
法一：暴力
枚举任意一个点的复杂度为 ，所以枚举两个点，再加上检测的复杂度时间，总体复杂度为 。
法二：前缀和优化
考虑到全 1 矩阵，包含 1 的个数确定，所以可以优化到 ，仍然无法承受。
法三：换方向枚举
枚举全1矩阵的上下边界，然后将二维数组压缩到一维去处理，变为最大子段和问题，复杂度 或
法四：单调栈
枚举全 1 矩阵的下边界 i，然后 表示以 开始，从上走最多有多少个连续的 1 。然后在 数组中找最大矩形。复杂度

其他：注意到题目输入是单个 char，所以最好用 cin 来输入，避免了手动getcchar处理空格换行等问题。
另外可以用 ios::sync_with_stdio(false); cin.tie(nullptr); 来关闭 cin 同步，加快输入。

#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
int a[N][N];
int n, m;
int st[N], h[N], tp, w[N];
int main(){
    ios::sync_with_stdio(false); cin.tie(nullptr);
    cin >> n >> m;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            char c;cin >> c;
            if(c == 'F')a[i][j] = 1;
        }
    }
    int res = 0;
    for(int i=1;i<=n;i++){
        tp = 0;
        for(int j=1;j<=m+1;j++){
            if(a[i][j]) h[j] = h[j] + 1;
            else h[j] = 0;
            int width = 0;
            while(tp && st[tp] >= h[j]){
                width += w[tp];
                res = max(res,width * st[tp]);
                tp--;
            }
            width ++;
            st[++tp] = h[j];
            w[tp] = width;
        }
    }
    cout << res * 3 << endl;
    return 0;
}

双栈排序

Tom 最近在研究一个有趣的排序问题。通过 个栈 和 ，Tom 希望借助以下 种操作实现将输入序列升序排序。

• 操作：如果输入序列不为空，将第一个元素压入栈
• 操作：如果栈 不为空，将 栈顶元素弹出至输出序列
• 操作：如果输入序列不为空，将第一个元素压入栈
• 操作：如果栈 不为空，将 栈顶元素弹出至输出序列

如果一个 的排列 可以通过一系列操作使得输出序列为 %2C%20n#card=math&code=1%2C%202%2C%E2%80%A6%2C%28n-1%29%2C%20n&id=K8ovz)，Tom 就称 是一个”可双栈排序排列”。
例如 #card=math&code=%281%2C%203%2C%202%2C%204%29&id=wb25f) 就是一个”可双栈排序序列”，而 #card=math&code=%282%2C%203%2C%204%2C%201%29&id=JeY4X) 不是。
下图描述了一个将 #card=math&code=%281%2C%203%2C%202%2C%204%29&id=zIk1M) 排序的操作序列：<a, c, c, b, a, d, d, b>

当然，这样的操作序列有可能有几个，对于上例 #card=math&code=%281%2C%203%2C%202%2C%204%29&id=pNx1v)，<a, c, c, b, a, d, d, b>是另外一个可行的操作序列。Tom 希望知道其中字典序最小的操作序列是什么。
输入格式
第一行是一个整数 。第二行有 个用空格隔开的正整数，构成一个 的排列。
输出格式
输出共一行，如果输入的排列不是”可双栈排序排列”，输出数字 。否则输出字典序最小的操作序列，每两个操作之间用空格隔开，行尾没有空格。
数据范围

输入样例：

4
1 3 2 4

输出样例：

a b a a b b a b

如果只有一个栈，那么操作是固定的：
从前往后遍历每个数，将该数压入栈中，如果后面的数字都比栈顶数字要大，那么栈顶元素出栈（该操作一直进行，直到条件不被满足）
因此，我们只需要思考每个数字分配到哪个栈中。
根据上面的弹出顺序，可以知道，不论是单栈还是双栈，如果一个数字后面还有比它小的数字，那么这个数字是不能够被及时弹出的。
所以，若 ，然后有一个 并且 ，那么 与 一定不能放在同一个栈中。
因为，在 出栈之前，是不能够出栈的，因此 也不能在 后面入同一个栈。
所以，我们需要预处理出所有有矛盾的二元组 ，然后进行二分图染色就可以确定每个元素该入哪一个栈了。

证明： 上面的论述已经证明了必要性，即答案必须是满足该性质的，然后下面证明充分性，即满足该性质的一定符合答案。 我们考虑 入栈时的操作，在该栈中，所有元素都是大于 的，因为原本该栈中那些小于 的元素 都已经出栈了（因为 在 后面并没有比 小的元素了）。所以栈中一定是单调递减的，这样就一定可以构造出答案。

然后再来说说字符方案最近该怎么处理。
该题在 2020 年以前，洛谷以及 Acwing 的数据都是不够强的，在字典序最小这块有很多代码可以被 hack。
入栈操作要比出栈操作优先，另外，对第一个栈操作要比对第二个栈操作优先。
在每个元素入栈之前，是必须要保证单调性的，但出栈元素在每个时刻是被唯一指定的，所以有可能两个栈都需要出栈。
也就是说，我们原本的想法是能出栈就出栈，但现在是，由于栈 2 出栈操作不如栈 1 入栈操作，所以如果栈 2 需要出栈了也不一定要立即出栈，可以先让栈 1 入栈。所以在栈 1 入栈之前需要特殊判断。
具体来说：
当前元素要入第一个栈：

1. 如果栈 1 栈顶要出栈，则优先出栈（栈 1 出栈是要立刻出的）
2. 栈 1 出栈完毕，如果栈 1 栈顶要比当前元素小（不满足单调性，那么栈 2 也不得不出栈），那么此时栈 2 与栈 1 相互出栈（直到 栈 1栈顶比当前元素大）。
3. 元素入栈

当前元素要入第二个栈：

1. 栈 1 栈 2 能出栈就出栈

2. 元素入栈

   #include <bits/stdc++.h>
   using namespace std;
   typedef long long ll;
   const int inf = 0x3f3f3f3f;
   const int N = 1010 + 5;
   int n, a[N], f[N];
   int color[N];
   bool g[N][N];
   stack<int> stk1, stk2;
   int now = 1;
   bool dfs(int u,int c){
    color[u] = c;
    for (int i = 1; i <= n;i++)
        if(g[u][i]){
            if(color[i] == c)
                return false;
            if(color[i] == -1 && !dfs(i,!c))
                return false;
        }
    return true;
   }
   void pop() {
    while (true) {
        if (stk1.size() && stk1.top() == now) {
            stk1.pop();
            cout << "b ";
            now++;
        }
        else if (stk2.size() && stk2.top() == now) {
            stk2.pop();
            cout << "d ";
            now++;
        }
        else break;
    }
   }
   int main() {
    cin >> n;
    for (int i = 1; i <= n;i++)
        scanf("%d", &a[i]);
    f[n + 1] = n + 1;
    memset(g, false, sizeof g);
    for (int i = n; i;i--)
        f[i] = min(f[i + 1], a[i]);
    for (int i = 1; i <= n;i++)
        for (int j = i + 1; j <= n;j++)
        if(a[i] < a[j] && f[j+1] < a[i])
            g[i][j] = g[j][i] = true;
    memset(color, -1, sizeof color);
    int flag = true;
    for (int i = 1; i <= n;i++){
        if(color[i] == -1 && !dfs(i,0)){
            flag = false;
            break;
        }
    }
    if(flag == false){
        puts("0");
        return 0;
    }
    for (int i = 1; i <= n; i++) {
        if (color[i] == 0) {
            while (stk1.size() && stk1.top() == now) {
                stk1.pop();
                cout << "b ";
                now++;
            }
            while(stk1.size() && a[i] > stk1.top()) {
                if (stk1.size() && stk1.top() == now) {
                    stk1.pop();
                    cout << "b ";
                    now++;
                }
                else if (stk2.size() && stk2.top() == now) {
                    stk2.pop();
                    cout << "d ";
                    now++;
                }
                else break;
            }
            stk1.push(a[i]);
            cout << "a ";
        }
        else {
            pop();
            stk2.push(a[i]);
            cout << "c ";
        }
    }
    pop();
    cout << endl;
    return 0;
   }

滑动窗口

给定一个大小为 的数组。
有一个大小为 的滑动窗口，它从数组的最左边移动到最右边。
你只能在窗口中看到 个数字。
每次滑动窗口向右移动一个位置。
以下是一个例子：
该数组为 [1 3 -1 -3 5 3 6 7]， 为 。
你的任务是确定滑动窗口位于每个位置时，窗口中的最大值和最小值。
输入格式
输入包含两行。
第一行包含两个整数 和 ，分别代表数组长度和滑动窗口的长度。
第二行有 个整数，代表数组的具体数值。
同行数据之间用空格隔开。
输出格式
输出包含两个。
第一行输出，从左至右，每个位置滑动窗口中的最小值。
第二行输出，从左至右，每个位置滑动窗口中的最大值。
输入样例：

8 3
1 3 -1 -3 5 3 6 7

输出样例：

-1 -3 -3 -3 3 3
3 3 5 5 6 7

最大值与最小值的问题是等价的，我们只讨论最大值的情况。
在滑动窗口问题中求解最大值，维护一个单调队列（单调递减）：

1. 对于每个位置 i，首先将所有坐标小于等于 i - k 的数字都删掉
2. 然后 入队之前，将队尾元素小于等于 的也删掉
3. 入队

4. 此时队头元素即当前窗口的最大值元素

   #include <bits/stdc++.h>
   using namespace std;
   const int N = 1000010;
   int n, k, a[N];
   int q1[N], l1, r1, q2[N], l2, r2;
   int rs[N], rs2[N];
   int main(){
    l1 = r2 = 0;
    r1 = r2 = -1;
    scanf("%d%d", &n, &k);
    for(int i=1;i<=n;i++){
        scanf("%d", &a[i]);
        while(l1 <= r1 && q1[l1] <= i - k) l1 ++;
        while(l2 <= r2 && q2[l2] <= i - k) l2 ++;
        while(l1 <= r1 && a[q1[r1]] >= a[i]) r1 --;
        while(l2 <= r2 && a[q2[r2]] <= a[i]) r2 --;
        q1[++r1] = i;
        q2[++r2] = i;
        if(i >= k) {
            rs[i] = a[q1[l1]];
            rs2[i] = a[q2[l2]];
        }
    }
    for(int i=k;i<=n;i++) printf("%d ", rs[i]);
    puts("");
    for(int i=k;i<=n;i++) printf("%d ", rs2[i]);
    return 0;
   }

   内存分配

   内存是计算机重要的资源之一，程序运行的过程中必须对内存进行分配。
   经典的内存分配过程是这样进行的：

5. 内存以内存单元为基本单位，每个内存单元用一个固定的整数作为标识，称为地址。地址从 开始连续排列，地址相邻的内存单元被认为是逻辑上连续的。我们把从地址 开始的 个连续的内存单元称为首地址为 长度为 的地址片。

6. 运行过程中有若干进程需要占用内存，对于每个进程有一个申请时刻 ，需要内存单元数 及运行时间 。在运行时间 内（即 时刻开始， 时刻结束），这 个被占用的内存单元不能再被其他进程使用。
7. 假设在T时刻有一个进程申请 个单元，且运行时间为 ，则：
   1. 若 时刻内存中存在长度为 的空闲地址片，则系统将这 个空闲单元分配给该进程。若存在多个长度为 个空闲地址片，则系统将首地址最小的那个空闲地址片分配给该进程。
   2. 如果 时刻不存在长度为 的空闲地址片，则该进程被放入一个等待队列。对于处于等待队列队头的进程，只要在任一时刻，存在长度为 的空闲地址片，系统马上将该进程取出队列，并为它分配内存单元。注意，在进行内存分配处理过程中，处于等待队列队头的进程的处理优先级最高，队列中的其它进程不能先于队头进程被处理。

现在给出一系列描述进程的数据，请编写一程序模拟系统分配内存的过程。

输入格式
第一行是一个数 ，表示总内存单元数（即地址范围从 到 ）。
从第二行开始每行描述一个进程的三个整数 。
最后一行用三个 表示结束。
数据已按 从小到大排序。
输入文件最多 行，且所有数据都小于 。
输入文件中同一行相邻两项之间用一个或多个空格隔开。

输出格式
输出包括 行。
第一行是全部进程都运行完毕的时刻。
第二行是被放入过等待队列的进程总数。

输入样例：

10
1 3 10
2 4 3
3 4 4
4 1 4
5 3 4
0 0 0

输出样例：

12
2

提示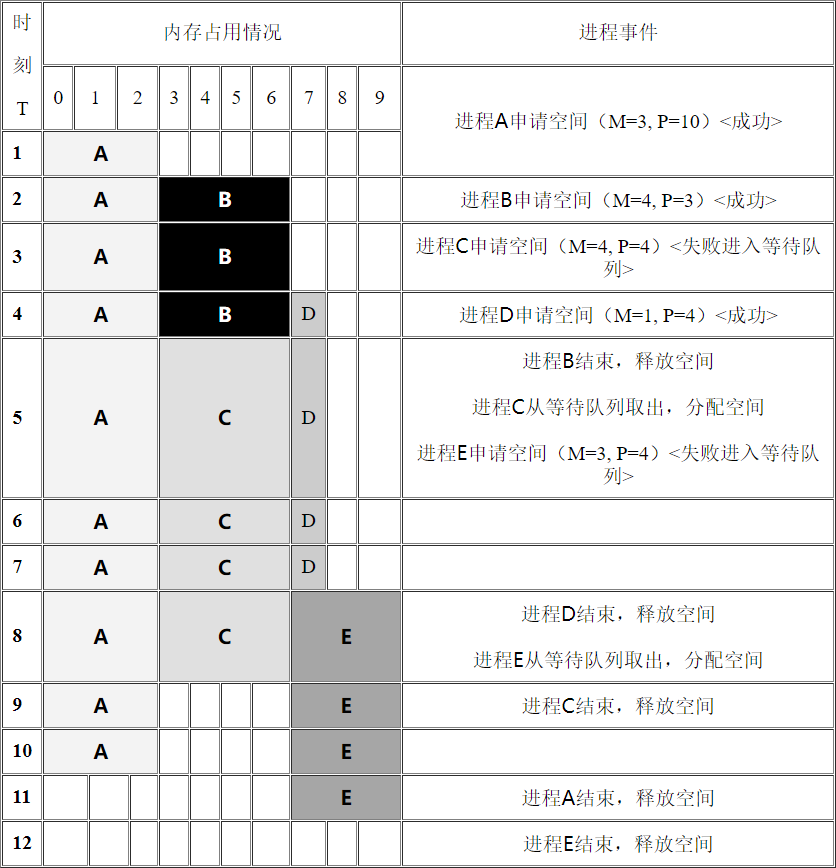

该题是 NOI 1999 的题目。
已经用的空间，我们用一段一段的区间表示，由于没有交集，所以直接按照左端点排序即可。
更取巧的做法，我们直接用 map 去存这些区间 map[l] = r 表示左端点为 l 的区间，右端点为 r。由于 map 内部是红黑树，所以是按照 l 排好序的。
每次插入一个新任务，从头遍历 map，找到足够大的空间，如果找不到就放入队列。
插入成功的任务，要按照 <结束时间，区间左端点l> 的形式放入优先队列，然后及时的去删除即可。
注意，如果优先队列队头任务的结束时间是 t，那么应当把所有 t 时刻结束的任务都出队，然后考虑候补队列中的任务能否在 t + 1 时刻插入到内存中。这一操作必须及时进行。需要双层 while 来实现。

#include<bits/stdc++.h>
using namespace std;
#define dbg(x...) do { cout << "\033[32;1m" << #x <<" -> "; err(x); } while (0)
void err() { cout << "\033[39;0m" << endl; }
template<class T, class... Ts> void err(const T& arg,const Ts&... args) { cout << arg << " "; err(args...); }
#define fi first
#define se second
#define pb push_back
#define rep(i,j,k) for (int i = int(j); i <= int(k); i++)
#define per(i,j,k) for(int i=int(j);i>=int(k);i--)
#define all(V) V.begin(), V.end()
typedef unsigned long long ull;
typedef long long ll;
typedef pair<int,int> PII;
typedef pair<long long, long long> pll;
int n, t, m, p, cnt, res;
map<int, int> mp;
queue<PII> q;
priority_queue<PII, vector<PII>, greater<PII>> pq;
bool add(int t, int m, int p) {
    for(auto it = mp.begin(); it != mp.end(); it++){
        auto jt = next(it);
        if(jt != mp.end() && (jt->first - it->second - 1 >= m)) {
            mp[it->second + 1] = it->second + m;
            pq.push({t + p, it->second + 1});
            return true;
        }
    }
    return false;
}
void finish(int t) {
    while(pq.size() && pq.top().first <= t) {
        int curt = pq.top().first;
        while(pq.size() && pq.top().first == curt) {
            auto top = pq.top();
            pq.pop();
            mp.erase(top.second);
        }
        res = curt;
        while(q.size()) {
            auto front = q.front();
            if(add(curt, front.first, front.second)) {
                q.pop();
            } else break;
        }
    }
}
void solve() {
    cin >> n;
    mp[-1] = -1; mp[n] = n;
    while(cin >> t >> m >> p) {
        if(!t && !m && !p) break;
        finish(t);
        if(!add(t, m, p)) {
            q.push({m, p});
            cnt ++;
        }
    }
    finish(2E9);
    cout << res << "\n" << cnt << "\n";
}
int main(){
    ios::sync_with_stdio(false); cin.tie(nullptr);
    int T; T = 1;
    while(T--) {
        solve();
    }
}

矩阵

给定一个 行 列的 矩阵（只包含数字 或 的矩阵），再执行 次询问，每次询问给出一个 行 列的 矩阵，求该矩阵是否在原矩阵中出现过。

输入格式
第一行四个整数 。
接下来一个 行 列的 矩阵，数字之间没有空格。
接下来一个整数 。
接下来 个 行 列的 矩阵，数字之间没有空格。

输出格式
对于每个询问，输出 表示出现过， 表示没有出现过。
数据范围
，，
输入样例：

3 3 2 2
111
000
111
3
11
00
11
11
00
11

输出样例：

1
0
1

二维字符串哈希
首先，我们只对第行处理，表示 这一前缀的哈希值。
然后，我们在对第列处理，
那么如何来求一个子矩阵的哈希？
对于以 为右下角，x 轴长度为 a，y 轴长度为 b 的子矩阵：

至此，提前将所有固定长度的子矩阵存入哈希表（set 或map），然后每次查询时，直接去查哈希表是否存在即可。

#include <bits/stdc++.h>
using namespace std;
typedef unsigned long long ull;
const int N = 1010;
const int base1 = 131,base2 = 13331;
int n,m,a,b,q;
char s[N][N];
ull d[N][N],d2[N][N],p1[N],p2[N];
set<ull> st;
inline ull calc(int x,int y){//a b
    return d[x][y] - d[x-a][y] * p2[a] - d[x][y-b] * p1[b] + d[x-a][y-b] * p2[a] * p1[b];
}
int main(){
    scanf("%d%d%d%d",&n,&m,&a,&b);
    p1[0] = p2[0] = 1;
    for(int i=1;i<=n;i++)p1[i] = p1[i-1] * base1;
    for(int i=1;i<=m;i++)p2[i] = p2[i-1] * base2;
    for(int i=1;i<=n;i++){
        scanf("%s",s[i]+1);
        for(int j=1;j<=m;j++){
            d[i][j] = d[i][j-1] * base1 + s[i][j];
        }
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            d[i][j] = d[i-1][j] * base2 + d[i][j];
            if(i >= a && j >= b)st.insert(calc(i,j));
        }
    }
    scanf("%d",&q);
    while(q--){
        for(int i=1;i<=a;i++){
            scanf("%s",s[i] + 1);
            for(int j=1;j<=b;j++){
                d[i][j] = d[i][j-1] * base1 + s[i][j];
            }
        }
        for(int i=1;i<=a;i++){
            for(int j=1;j<=m;j++){
                d[i][j] = d[i-1][j] * base2 + d[i][j];
            }
        }
        if(st.find(d[a][b]) != st.end()){
            puts("1");
        }else puts("0");
    }
    return 0;
}

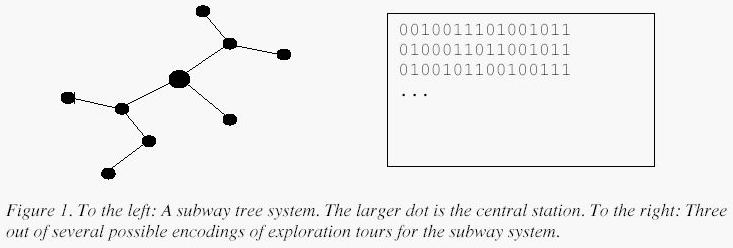
树形地铁系统

一些主要城市拥有树形的地铁系统，即在任何一对车站之间，有且只有一种方式可以乘坐地铁。
此外，这些城市大多数都有一个中央车站。
想象一下，你是一名在拥有树形地铁系统的城市游玩的游客，你想探索该城市完整的地铁线路。
你从中央车站出发，随机选择一条地铁线，然后乘坐地铁行进。
每次到达一个车站，你都将选择一条尚未乘坐过的地铁线路进行乘坐。
如果不存在未乘坐过的线路，则退回到上一个车站，再做选择。
直到你将所有地铁线路都乘坐过两次（往返各一次），此时你将回到中央车站。
之后，你以一种特殊的方式回忆自己的坐车过程，你将你的完整地铁乘坐路线编码为一个二进制字符串。
其中 编码表示你乘坐地铁线路到达距离中央车站更远的一站， 编码表示你乘坐地铁线路到达距离中央车站更近的一站。

输入格式
第一行输入一个正整数 ，代表测试用例数量。
每个测试用例由两行组成，每行输入一个由字符 和 构成的字符串，长度最多为 ， 两个字符串都描述了一种树形地铁系统的正确探索路线。

输出格式
对于每个测试用例，如果两个字符串描述的探索路线可以视为同一个地铁系统的两种探索路线，则输出 same。
否则，输出 different。
每行输出一个结果。

输入样例：

2
0010011101001011
0100011011001011
0100101100100111
0011000111010101

输出样例：

same
different

回想树的 DFS 序。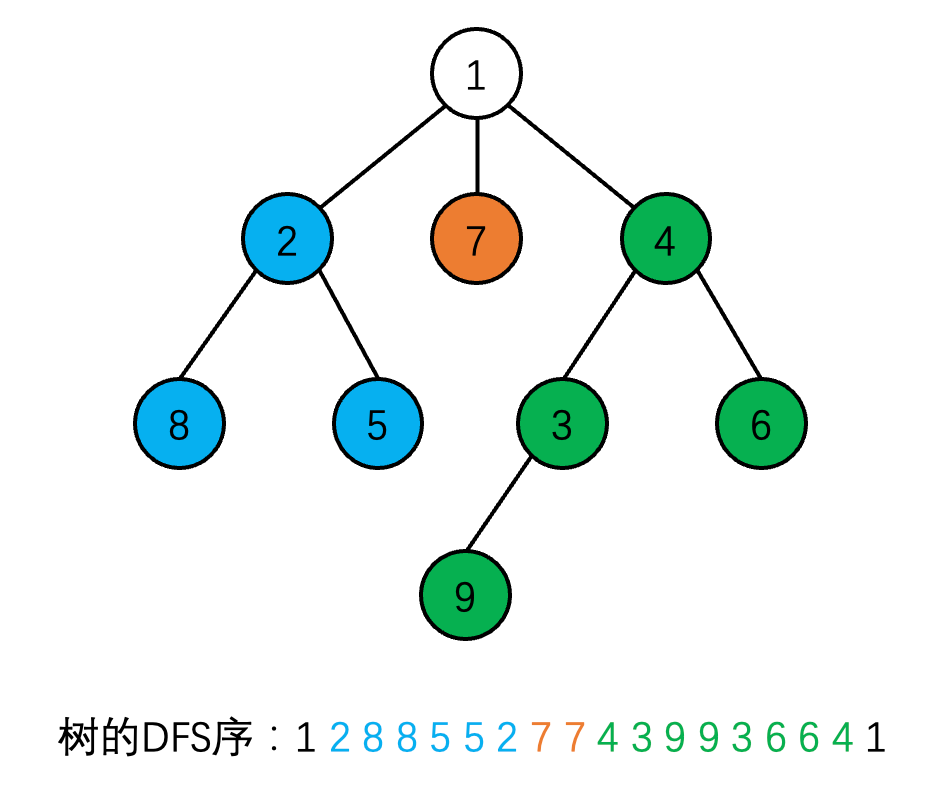

每个节点都会出现两次，对应进和出，也就是本题中的 0 和 1。
对于当前根节点的每个子树，我们不妨，将这些子树的 DFS 序，按照字典序排好序。那么如果两个树可以是同构的（已经提前指定了对应根的前提下），那么排好序的 DFS 也是相同的。

#include <bits/stdc++.h>
using namespace std;
int T;
string dfs(string& x,int &u){
    vector<string> v;
    u++; // 根进
    while(x[u] == '0')v.push_back(dfs(x,u));
    u++; // 根出
    sort(v.begin(),v.end());
    string res = "0";
    for(string s : v) res += s;
    res += '1';
    return res;
}
int main(){
    scanf("%d",&T);
    while(T--){
        string a,b;
        cin >> a >> b;
        // 由于根也需要一次进出，所以在头尾需要补齐。
        a = '0' + a + '1';
        b = '0' + b + '1';
        int ua = 0,ub = 0;
        if(dfs(a,ua) == dfs(b,ub))puts("same");
        else puts("different");
    }
    return 0;
}

项链

有一天，达达捡了一条价值连城的宝石项链，但是，一个严重的问题是，他并不知道项链的主人是谁！
在得知此事后，很多人向达达发来了很多邮件，都说项链是自己的，要求他归还（显然其中最多只有一个人说了真话）。
达达要求每个人都写了一段关于自己项链的描述： 项链上的宝石用数字 至 来标示。
一个对于项链的表示就是从项链的某个宝石开始，顺指针绕一圈，沿途记下经过的宝石，比如项链： ，它的可能的四种表示是 。
达达现在心急如焚，于是他找到了你，希望你能够编写一个程序，判断两个给定的描述是否代表同一个项链（注意，项链是不会翻转的）。
也就是说给定两个项链的表示，判断他们是否可能是一条项链。
输入格式
输入文件只有两行，每行一个由字符 至 构成的字符串，描述一个项链的表示（保证项链的长度是相等的）。
输出格式
如果两个对项链的描述不可能代表同一个项链，那么输出 No，否则的话，第一行输出一个 Yes，第二行输出该项链的字典序最小的表示。
数据范围
设项链的长度为 ，
输入样例：

2234342423
2423223434

输出样例：

Yes
2234342423

最小表示法模版题

string min_express(string& s) {
    int n = s.size();
    if(n == 0) return s;
    int i = 0, j = 1, k = 0;
    while(k < n && i < n && j < n) {
        if(s[(i + k) % n] == s[(j + k) % n]) k ++;
        else {
            s[(i + k) % n] > s[(j + k) % n] ? i += k + 1 : j += k + 1;
            if(i == j) i ++;
            k = 0;
        }
    }
    i = min(i, j);
    return s.substr(i) + s.substr(0, i);
}
void solve() {
  string s, t;
  cin >> s >> t;
  s = min_express(s); t = min_express(t);
  if(s == t) {
    cout << "Yes\n" << s << "\n";
  } else {
    cout << "No\n";
  }
}

奶牛矩阵

每天早上，农夫约翰的奶牛们被挤奶的时候，都会站成一个 行 列的方阵。
现在在每个奶牛的身上标注表示其品种的大写字母，则所有奶牛共同构成了一个 行 列的字符矩阵。
现在给定由所有奶牛构成的矩阵，求它的最小覆盖子矩阵的面积是多少。
如果一个子矩阵无限复制扩张之后得到的矩阵能包含原来的矩阵，则称该子矩阵为覆盖子矩阵。
输入格式
第 行：输入两个用空格隔开的整数， 和 。
第 行：描绘由奶牛构成的 行 列的矩阵，每行 个字符，字符之间没有空格。
输出格式
输出最小覆盖子矩阵的面积。（每个字符的面积为 ）
数据范围
,

输入样例：

2 5
ABABA
ABABA

输出样例：

2

提示
样例中给出的矩阵的最小覆盖子矩阵为 ，面积为 。

观察数据，大致可以使用 复杂度的算法。
由于最小覆盖矩阵可以无限扩展至所有，我们只需要考虑从最左上角开始的那一小块。

1. 尝试从小到大枚举 ，然后找到一个最小的 ，满足对于所有行都以为单位构成重复单元。具体来说对于第 i 行字符串 有 ，该操作复杂度为 。
2. 然后从列的角度去考虑，将每一行的字符串看做是一个元素，那么 行共有 个元素，比较每个元素是否相同需要 的复杂度，所以如果对这个长度为 的序列做 的话，时间复杂度为 。

   const int N = 10010;
   const int M = 100;
   const int p = 131;
   int n, m, nxt[N];
   char s[N][M];
   bool st[M];
   int main()
   {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n;i++){
        scanf("%s", s[i] + 1);
        for (int j = 1; j <= m;j++){
            bool flag = true;
            for (int u = j + 1; u <= m; u += j ){
                for (int l = 0; l < j && u+l <= m;l++){
                    if(s[i][l+1] != s[i][u+l]){
                        flag = false;
                        break;
                    }
                }
                if(!flag)
                    break;
            }
            if(!flag)
                st[j] = 1;
        }
    }
    int width = 0;
    for (int i = 1; i <= m;i++)if(st[i] == 0){
            width = i;
            break;
    }
    {
        for (int i = 1; i <= n;i++)
            s[i][width + 1] = 0;
        for(int i=2,j=0;i<=n;i++)
        {
            while (j && strcmp(s[i]+1, s[j+1]+1))
                j = nxt[j];
            if(strcmp(s[i]+1,s[j+1]+1) == 0)j++;
            nxt[i] = j;
        }
    }
    int height = n - nxt[n];
    cout << height * width << endl;
    return 0;
   }

匹配统计

阿轩在纸上写了两个字符串，分别记为 和 。
利用在数据结构与算法课上学到的知识，他很容易地求出了“字符串 从任意位置开始的后缀子串”与“字符串 ”匹配的长度。
不过阿轩是一个勤学好问的同学，他向你提出了 个问题：
在每个问题中，他给定你一个整数 ，请你告诉他有多少个位置，满足“字符串 从该位置开始的后缀子串”与 匹配的长度恰好为 。
例如：，则 有 这 个后缀子串，它们与 的匹配长度分别是 。
因此 有 个位置与 的匹配长度恰好为 ，有 个位置的匹配长度恰好为 ，有 个位置的匹配长度恰好为 。

输入格式
第一行输入三个整数 ，分别表示 串长度、串长度、问题个数。
第二行输入字符串 ，第三行输入字符串 。
接下来 行每行输入 个整数 ，表示一个问题。

输出格式
输出共 行，依次表示每个问题的答案。

数据范围

输入样例：

6 2 5
aabcde
ab
0
1
2
3
4

输出样例：

4
1
1
0
0

原问题要求，有多少个 A 的后缀与 B 匹配的长度恰好为 。
由于 的范围并不大，我们先尝试解决，对于一个确定的 的后缀，它与 的匹配长度，然后将其压入一个桶中记录即可。
暴力求解该问题的复杂度为 ，我们试图寻找更快的做法。

该题需要前置知识：扩展 KMP。
扩展 KMP 需要求解一个 数组，为字符串 与以 开头的后缀的最长公共前缀。
特别的，。（为了后面计算，但其实按照定义应当是 ）
我们称 为一个匹配段，在求解过程中，我们维护一个右端点最靠右的匹配段，记作 。

• 若 ，那么 ，因此
  • 紧接着，我们继续判断 是否等于 ，然后另 z[i]++ ，只到不能扩展为止。
• 若 ，我们按照朴素算法来求 即可，其实就是 z[i]=0，然后不断扩展。

最后，我们尝试用 来更新 。

// 注：以下代码下标从 0 开始
void exkmp(string& s, vector<int>& z) {
    int n = s.size();
    z.resize(n, 0);
    for(int i = 1, l = 0, r = 0; i < n; i++){
        if(i <= r) z[i] = min(r - i + 1, z[i - l]);
        while(i + z[i] < n && s[i + z[i]] == s[z[i]]) z[i] ++;
        if(i + z[i] - 1 > r) {
            l = i; r = i + z[i] - 1;
        }
    }
}

然后我们回到本题。
我们需要先求出 串的 数组，然后尝试用它来求解问题。
然后类似的，我们设 为以 为开头的后缀与 B 的最长公共前缀，然后就可以用类似求解 z 数组的方法去求解 d 了。

void exkmp(string& s, vector<int>& z) {
    int n = s.size();
    z.resize(n, 0);
    for(int i = 1, l = 0, r = 0; i < n; i++){
        if(i <= r) z[i] = min(r - i + 1, z[i - l]);
        while(i + z[i] < n && s[i + z[i]] == s[z[i]]) z[i] ++;
        if(i + z[i] - 1 > r) {
            l = i; r = i + z[i] - 1;
        }
    }
}
void solve() {
  int n, m, q;
  string s, t;
  cin >> n >> m >> q;
  cin >> s >> t;
  vector<int> z(m), d(n);
  unordered_map<int, int> mp;
  exkmp(t, z);
  for(int i = 0, l = 0, r = 0; i < n; i++) {
    if(i <= r) d[i] = min(r - i + 1, z[i - l]); // 注意这里的细节
    while(i + d[i] < n && d[i] < m && s[i + d[i]] == t[d[i]]) d[i] ++;
    if(i + d[i] - 1 > r) {
      l = i, r = i + d[i] - 1;
    }
    mp[d[i]] ++;
  }
  while(q --) {
    int x; cin >> x;
    cout << mp[x] << "\n";
  }
}

电话列表

给出一个电话列表，如果列表中存在其中一个号码是另一个号码的前缀这一情况，那么就称这个电话列表是不兼容的。
假设电话列表如下：

• Emergency 911
• Alice 97 625 999
• Bob 91 12 54 26

在此例中，报警电话号码（911）为 Bob 电话号码（91 12 54 26）的前缀，所以该列表不兼容。
输入格式
第一行输入整数 ，表示测试用例数量。
对于每个测试用例，第一行输入整数 ，表示电话号码数量。
接下来 行，每行输入一个电话号码，号码内数字之间无空格，电话号码不超过 位。
输出格式
对于每个测试用例，如果电话列表兼容，则输出 YES。
否则，输出 NO。
数据范围
,

输入样例：

2
3
911
97625999
91125426
5
113
12340
123440
12345
98346

输出样例：

NO
YES

Trie 树模版题。全部插入后，一一检测即可。

#include <bits/stdc++.h>
using namespace std;
int n,T,tr[100010][10],tot,cnt[100010];
char s[100010][12];
void insert(char *s){
    int len = strlen(s);
    int p = 0;
    for(int i=0;i<len;i++){
        int t = s[i] - '0';
        if(!tr[p][t]){
            tr[p][t] = ++tot;
        }
        p = tr[p][t];
    }
    cnt[p] = 1;
}
bool check(char *s){
    int len = strlen(s);
    int p = 0;
    for(int i=0;i<len-1;i++){
        int t = s[i] - '0';
        p = tr[p][t];
        if(cnt[p]){
            return true;   
        }
    }
    p = tr[p][s[len-1]-'0'];
    if(cnt[p] > 1)return true;
    return false;
}
int main(){
    scanf("%d",&T);
    while(T--){
        for(int i=0;i<=tot;i++){
            memset(tr[i],0,sizeof tr[i]);
            cnt[i] = 0;
        }
        tot = 0;
        scanf("%d",&n);
        bool flag = false;
        for(int i=1;i<=n;i++){
            scanf("%s",s[i]);
            insert(s[i]);
        }
        for(int i=1;i<=n;i++){
            if(check(s[i])){
                puts("NO");
                flag = true;break;
            }
        }
        if(!flag)puts("YES");
    }
    return 0;
}

黑盒子

黑盒子代表一个原始的数据库。
它可以用来储存整数数组，并且它拥有一个特殊变量 。
在最开始，黑盒子是空的，并且 。
现在对黑盒子进行一系列的操作处理，操作包括以下两种：

• ADD(x)：表示将 加入到黑盒子中。
• GET：使 增加 ，输出黑盒子中第 小的数值（即将所有数按升序排序后的第 个数）。

下面给出一个具体例子：

序号 操作        i     盒子内数（升序排列后）             输出的值 
1    ADD(3)      0     3   
2    GET         1     3                                    3 
3    ADD(1)      1     1, 3   
4    GET         2     1, 3                                 3 
5    ADD(-4)     2     -4, 1, 3   
6    ADD(2)      2     -4, 1, 2, 3   
7    ADD(8)      2     -4, 1, 2, 3, 8   
8    ADD(-1000)  2     -1000, -4, 1, 2, 3, 8   
9    GET         3     -1000, -4, 1, 2, 3, 8                1 
10   GET         4     -1000, -4, 1, 2, 3, 8                2 
11   ADD(2)      4     -1000, -4, 1, 2, 2, 3, 8