线段树

树状数组和线段树可谓是亲兄弟，但他两毕竟还有一些区别：

树状数组能有的操作，线段树一定有；

线段树有的操作，树状数组不一定有。

但是，并不是直接选择线段树而放弃学习树状数组。

与按照二进制位进行区间划分的树状数组相比，线段树是一种更加通用的结构：

  1. 线段树的每个节点都代表一个区间
  2. 线段树具有唯一的根节点，代表的区间是整个统计范围，如 线段树 - 图1
  3. 线段树的每个叶节点都代表一个长度为 1 的元区间线段树 - 图2
  4. 对于每个内部节点线段树 - 图3，它的左子节点是 线段树 - 图4, 右子节点是线段树 - 图5，其中 线段树 - 图6%2F2%5Crfloor#card=math&code=mid%20%3D%5Clfloor%28l%2Br%29%2F2%5Crfloor&id=S7gk9)

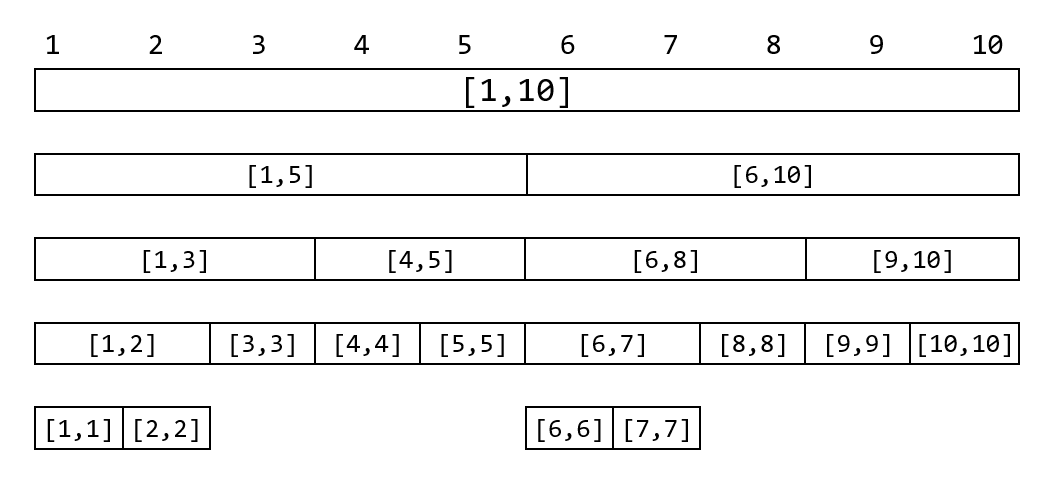
线段树 - 图7

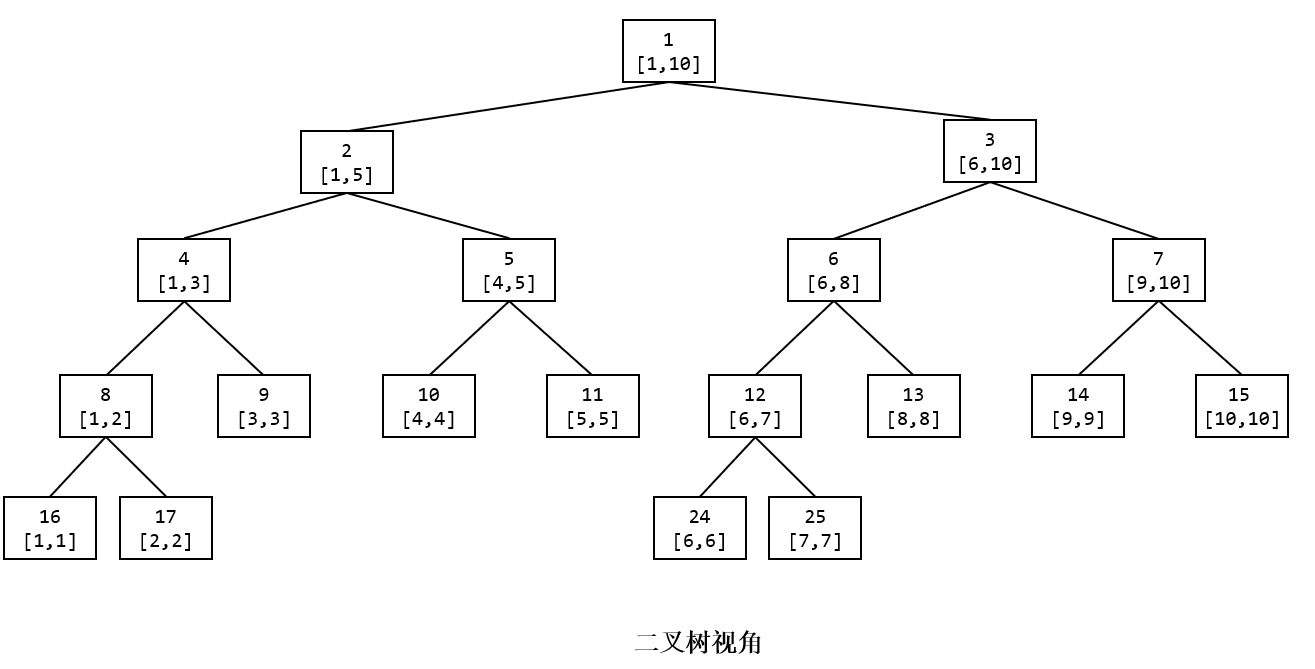
线段树 - 图8

上图展示了一颗线段树。可以发现，除去树的最后一层，整颗线段树一定是一颗完全二叉树，树的深度为 线段树 - 图9#card=math&code=O%28%5Clog%20N%29&id=HS08y)。因此，我们可以按照与二叉堆类似的“父子2倍”节点编号方法。

  1. 根节点编号为1
  2. 编号为 x 的节点，左子节点编号为 线段树 - 图10，右子节点编号为 线段树 - 图11。

使用一个 struct 数组来保存线段树，树的最后一层节点在数组汇总保存的位置不是连续的，直接空出数组中多余的位置即可。

理想情况下，线段树 - 图12 个叶子节点的满二叉树有 线段树 - 图13 个节点。

因为在上述存储方式下，最后还有一层产生了空余，所以保存线段树的数组长度要不小于 线段树 - 图14 才能保证不会越界。

线段树的建树

给定一个长度为 线段树 - 图15 的序列 线段树 - 图16，我们可以在区间 线段树 - 图17 上建立一颗线段树。

每个叶子结点 线段树 - 图18 保存 线段树 - 图19 的信息，由于线段树的二叉结构很容易的从下往上的传递信息，所以以求区间最大值为例。记 线段树 - 图20 ，显然有 线段树 - 图21#card=math&code=val%5Bl%2Cr%5D%20%3D%20max%28val%5Bl%2Cmid%5D%2C%20val%5Bmid%2B1%2C%20r%5D%29&id=WJGwW)

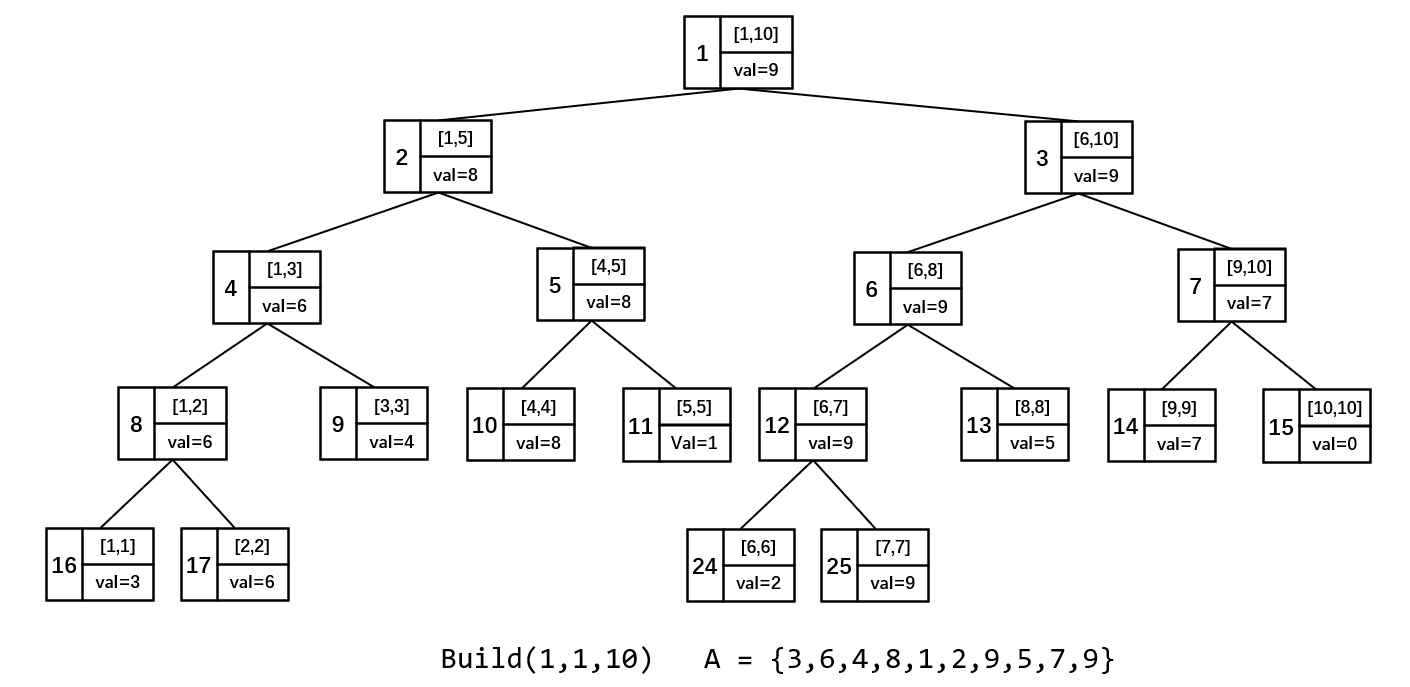
线段树 - 图22

  1. struct SegTree{
  2.     int l, r;
  3.     int val;
  4. }t[N*4]; // struct 数组存储线段树
  5. void build(int p, int l, int r){
  6.     t[p].l = l, t[p].r = r;
  7.     if(l == r) {t[p].val = a[l]; return;}
  8.     int mid = (l + r) / 2; // l + r >> 1
  9.     build(p*2, l, mid);
  10.     build(p*2+1, mid+1, r); 
  11.     t[p].val = max(t[p*2].val, t[p*2+1].val); // pushup()
  12. }
  13. build(1, 1, n); // 调用入口

单点修改

单调修改形如 线段树 - 图23 的指令，表示把 线段树 - 图24 的值修改为 v。

在线段树中，根节点（编号为 1 的节点）时执行各种命令的入口。我们需要从根节点出发，递归找到代表区间 线段树 - 图25 的叶节点，然后从下往上更新 线段树 - 图26 以及它的所有祖先节点上保存的信息。时间复杂度是 线段树 - 图27#card=math&code=O%28%5Clog%20N%29&id=PdOrQ)

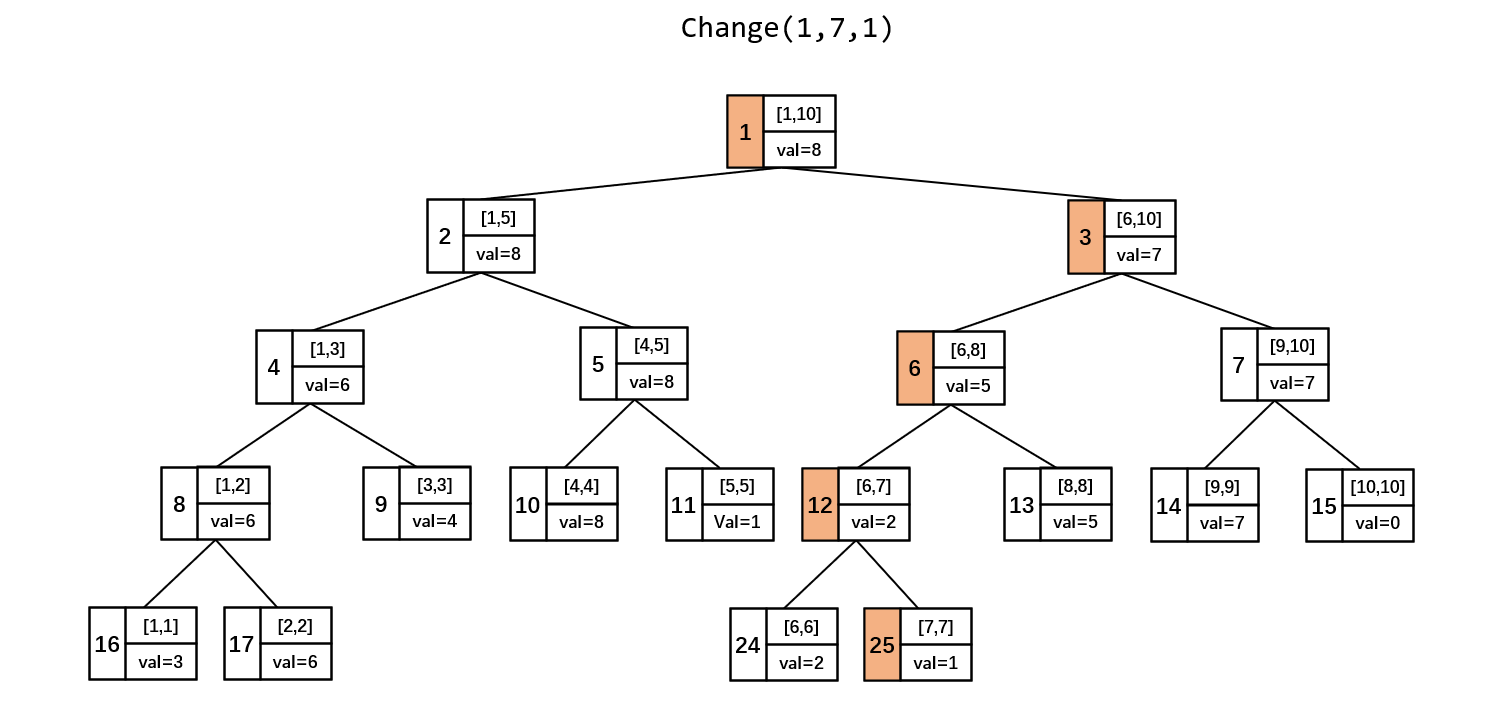
线段树 - 图28

  1. void change(int p, int x, int v){
  2.     if(t[p].l == t[p].r) {
  3.         t[p].val = v; return;
  4.     }
  5.     int mid = (t[p].l + t[p].r) / 2;
  6.     if(x <= mid) change(p*2, x, v);
  7.     else change(p*2+1, x, v);
  8.     t[p].val = max(t[p*2].val, t[p*2+1].val);
  9. }
  10. change(1,x,v); // 调用入口

线段树的区间查询

区间查询形如：“线段树 - 图29” 的指令，例如查序列 线段树 - 图30 在区间 线段树 - 图31 上的最大值，即线段树 - 图32 ，我们只需要从根节点开始，递归执行以下过程：

  1. 若 线段树 - 图33 完全覆盖了当前节点代表的区间，则立即回溯，并且该节点的 线段树 - 图34 值为候选答案。
  2. 若左子节点与 线段树 - 图35 有重叠部分，则递归访问左子节点
  3. 若右子节点与 线段树 - 图36 有重叠部分，则递归访问右子节点

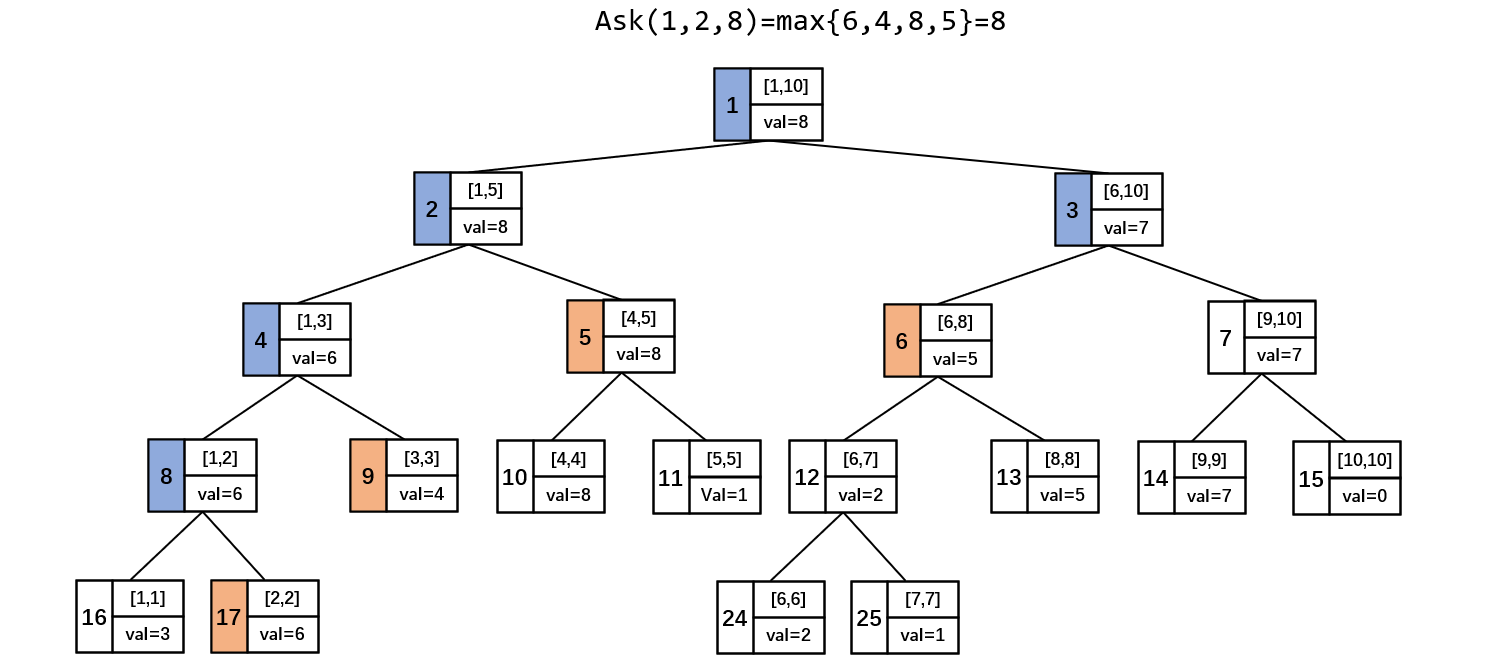
线段树 - 图37

  1. int ask(int p, int l, int r){
  2.     if(l <= t[p].l && r >= t[p].r) return t[p].val; // 完全包含
  3.     int mid = (t[p].l + t[p].r) / 2;
  4.     int val = - (1 << 30);
  5.     if(l <= mid) val = max(val, ask(p*2, l, r)); // 左子节点有重叠
  6.     if(r > mid) val = max(val, ask(p*2+1, l, r)); // 右子节点有重叠
  7.     return val;
  8. }
  9. cout << ask(1, l, r)  << endl; // 调用入口

该查询过程会把询问区间 线段树 - 图38 在线段树上分成 线段树 - 图39#card=math&code=O%28%5Clog%20N%29&id=U3fCy) 个节点，取它们的最大值作为答案。

为什么是 线段树 - 图40#card=math&code=O%28log%20N%29&id=VJ2Ip) 个呢？分析上述过程，在每个结点 线段树 - 图41 上，设 线段树 - 图42%2F2#card=math&code=mid%20%3D%20%28p_l%2Bp_r%29%2F2&id=yvefd) （向下取整），可能出现如下情况：

  1. 线段树 - 图43 ，完全覆盖当前结点，直接返回
  2. 线段树 - 图44 ，只有 线段树 - 图45 处于结点之内。
    1. 线段树 - 图46, 只会递归右子树
    2. 线段树 - 图47 ，虽然递归两颗子树，但是右子节点会在递归后直接返回（对应完全覆盖的情况）
  3. $ l\le p_l \le r \le p_r$ ，即只有 线段树 - 图48 处于结点之内，与情况 2 类似。
  4. 线段树 - 图49 ，即 线段树 - 图50 与 线段树 - 图51 都位于结点之内。
    1. 线段树 - 图52 都位于 线段树 - 图53 的一侧，则只会递归一颗子树
    2. 线段树 - 图54 分别位域 线段树 - 图55 的两侧，递归左右两颗子树。

可以发现，只有 4.2 会真正产生对左右两颗子树的递归，但这类情况最多只会发生一次，之后子节点上就会变成情况 2 或者情况 3.

所以 线段树 - 图56%20%3D%20O(%5Clog%20N)#card=math&code=O%282%5Clog%20N%29%20%3D%20O%28%5Clog%20N%29&id=EFK5D) 。从宏观上理解，相当于查询区间 线段树 - 图57 在线段树上划分出一条递归访问路径。情况 4.2 在两条路径在从下往上第一次交汇处产生。

线段树例题

例题1 区间最大连续子段和

SP1043 GSS1 - Can you answer these queries I

注：如果提交失败，可以去vjudge 进行提交。网址：https://vjudge.net/problem/SPOJ-GSS1

  1. #include <bits/stdc++.h>
  2. using namespace std;
  3. const int N = 50010;
  4. struct SegTree{
  5.     int l, r;
  6.     int sum, lmax, rmax, mmax;
  7. }t[N<<2];
  8. int n, m, a[N];
  9. void pushup(SegTree &p, SegTree ls, SegTree rs) {
  10.     p.sum = ls.sum + rs.sum;
  11.     p.lmax = max(ls.lmax, ls.sum + rs.lmax);
  12.     p.rmax = max(rs.rmax, rs.sum + ls.rmax);
  13.     p.mmax = max(ls.mmax, max(rs.mmax, ls.rmax+rs.lmax));
  14. }
  15. void build(int p, int l, int r) {
  16.     t[p].l = l, t[p].r = r;
  17.     if(l == r) {
  18.         t[p].sum = t[p].lmax = t[p].rmax = t[p].mmax = a[l];
  19.         return;
  20.     }
  21.     int mid = l + r >> 1;
  22.     build(p*2, l, mid);
  23.     build(p*2+1, mid+1, r);
  24.     pushup(t[p], t[p*2], t[p*2+1]);
  25. }
  26. SegTree query(int p, int l, int r) {
  27.     if(t[p].l >= l && t[p].r <= r) {
  28.         return t[p];
  29.     }
  30.     int mid = t[p].l + t[p].r >> 1;
  31.     if(l > mid) {
  32.         return query(p*2+1, l, r);
  33.     } else if(r <= mid) {
  34.         return query(p*2, l, r);
  35.     } else {
  36.         SegTree res;
  37.         pushup(res, query(p*2, l, r), query(p*2+1, l, r));
  38.         return res;
  39.     }
  40. }
  41. int main(){
  42.     scanf("%d", &n);
  43.     for(int i=1;i<=n;i++) scanf("%d", &a[i]);
  44.     build(1, 1, n);
  45.     scanf("%d", &m);
  46.     while(m--){
  47.         int l, r;
  48.         scanf("%d%d", &l, &r);
  49.         printf("%d\n", query(1, l, r).mmax);
  50.     }
  51.     return 0;
  52. }

例题2 带修改的区间最大连续子段和

SP1716 GSS3 - Can you answer these queries III

VJudge 提交网址：https://vjudge.net/problem/SPOJ-GSS3

  1. #include <bits/stdc++.h>
  2. using namespace std;
  3. const int N = 50010;
  4. struct SegTree{
  5.     int l, r;
  6.     int sum, lmax, rmax, mmax;
  7. }t[N<<2];
  8. int n, m, a[N];
  9. void pushup(SegTree &p, SegTree ls, SegTree rs) {
  10.     p.sum = ls.sum + rs.sum;
  11.     p.lmax = max(ls.lmax, ls.sum + rs.lmax);
  12.     p.rmax = max(rs.rmax, rs.sum + ls.rmax);
  13.     p.mmax = max(ls.mmax, max(rs.mmax, ls.rmax+rs.lmax));
  14. }
  15. void build(int p, int l, int r) {
  16.     t[p].l = l, t[p].r = r;
  17.     if(l == r) {
  18.         t[p].sum = t[p].lmax = t[p].rmax = t[p].mmax = a[l];
  19.         return;
  20.     }
  21.     int mid = l + r >> 1;
  22.     build(p*2, l, mid);
  23.     build(p*2+1, mid+1, r);
  24.     pushup(t[p], t[p*2], t[p*2+1]);
  25. }
  26. SegTree query(int p, int l, int r) {
  27.     if(t[p].l >= l && t[p].r <= r) {
  28.         return t[p];
  29.     }
  30.     int mid = t[p].l + t[p].r >> 1;
  31.     if(l > mid) {
  32.         return query(p*2+1, l, r);
  33.     } else if(r <= mid) {
  34.         return query(p*2, l, r);
  35.     } else {
  36.         SegTree res;
  37.         pushup(res, query(p*2, l, r), query(p*2+1, l, r));
  38.         return res;
  39.     }
  40. }
  41. void change(int p, int pos, int val) {
  42.     if(t[p].l == pos && t[p].r == pos) {
  43.         t[p].sum = t[p].rmax = t[p].lmax = t[p].mmax = val;
  44.         return;
  45.     }
  46.     int mid = t[p].l + t[p].r >> 1;
  47.     if(pos <= mid) change(p*2, pos, val);
  48.     else change(p*2+1, pos, val);
  49.     pushup(t[p], t[p*2], t[p*2+1]);
  50. }
  51. int main(){
  52.     scanf("%d", &n);
  53.     for(int i=1;i<=n;i++) scanf("%d", &a[i]);
  54.     build(1, 1, n);
  55.     scanf("%d", &m);
  56.     while(m--){
  57.         int op, l, r;
  58.         scanf("%d%d%d", &op, &l, &r);
  59.         if(op == 0) {
  60.             change(1, l, r);
  61.         } else {
  62.             printf("%d\n", query(1, l, r).mmax);
  63.         }
  64.     }
  65.     return 0;
  66. }

例题3 区间GCD

链接：https://ac.nowcoder.com/acm/contest/949/H?&headNav=acm （注：需要提前注册牛客网账号）

简要题意

小阳手中一共有 线段树 - 图58 个贝壳，每个贝壳都有颜色，且初始第 线段树 - 图59 个贝壳的颜色为 线段树 - 图60 。现在小阳有 3 种操作：

  1. 线段树 - 图61：给 [l,r] 区间里所有贝壳的颜色值加上 x 。
  2. 线段树 - 图62：询问 [l,r] 区间里所有相邻贝壳 颜色值的差（取绝对值） 的最大值（若 l=r 输出 0）。
  3. 线段树 - 图63 ：询问 [l,r] 区间里所有贝壳颜色值的最大公约数。

根据更相减损术（欧几里得算法），我们知道 线段树 - 图64%20%3D%20gcd(x%2C%20y-x)#card=math&code=gcd%28x%2C%20y%29%20%3D%20gcd%28x%2C%20y-x%29&id=qitYO)， 他可以进一步扩展到三个数字的情况：线段树 - 图65#card=math&code=gcd%28x%2C%20y-x%2C%20z-x%29&id=LF4VN)。实际上，读者用数学归纳法容易证明，该性质对任意多个整数都成立。

因此，我们构造一个长度为 N 的新数列 B，其中B[i] = A[i] - A[i-1] ，B[1] 可以为任意值（后面不参与具体运算）。数列 B 为 A 的差分序列，用线段树维护序列 B 的区间最大公约数和区间绝对值的最大值。

这样，对于操作2，可以直接在线段树中查询输出答案。对于操作3，等价于求 线段树 - 图66)#card=math&code=gcd%28A%5Bl%5D%2C%20ask%281%2C%20l%2B1%2C%20r%29%29&id=x7sjH)

对于操作 1，只有 B[l] 加了 x，B[r] 减掉了 x，所以在维护 B 的线段树上只需进行两次单点修改即可。

另外，询问时，还需要数列 A 的值，可额外用一个支持“区间增加，单点查询”的树状数组对数列 A进行维护。

  1. #include <bits/stdc++.h>
  2. using namespace std;
  3. const int N = 100010;
  4. int n, m, a[N];
  5. int gcd(int a, int b) {return b == 0 ? a : gcd(b, a % b);}
  6. namespace BIT {
  7.     int n, bit[N];
  8.     inline void init(int tot) {    
  9.         n = tot;
  10.         memset(bit, 0, sizeof bit);
  11.     }
  12.     inline void add(int x, int y){
  13.         for(;x<=n;x+=x&-x) bit[x] += y;
  14.     }
  15.     inline int query(int x) {
  16.         int ans = 0;
  17.         for(;x;x-=x&-x) ans += bit[x];
  18.         return ans;
  19.     }
  20. }
  21. namespace SGT {
  22.     struct SegTree{
  23.         int l, r;
  24.         int g, Max;
  25.     }t[N<<2];
  26.     int n;
  27.     void build(int p, int l, int r) {
  28.         t[p].l = l, t[p].r = r;
  29.         if(l == r) {
  30.             t[p].g = a[l] - a[l-1];
  31.             t[p].Max = abs(a[l] - a[l-1]);
  32.             return;
  33.         }
  34.         int mid = l + r >> 1;
  35.         build(p*2, l, mid);
  36.         build(p*2+1, mid+1, r);
  37.         t[p].g = gcd(t[p*2].g, t[p*2+1].g);
  38.         t[p].Max = max(t[p*2].Max, t[p*2+1].Max);
  39.     }
  40.     void init(int tot){ n = tot; build(1, 1, n);}
  41.     void change(int p, int pos, int val) {
  42.         if(t[p].l == pos && t[p].r == pos) {
  43.             t[p].g += val;
  44.             t[p].Max = abs(BIT::query(t[p].l) - BIT::query(t[p].l-1));
  45.             return ;
  46.         }
  47.         int mid = t[p].l + t[p].r >> 1;
  48.         if(pos <= mid) change(p*2, pos, val);
  49.         else change(p*2+1, pos, val);
  50.         t[p].g = gcd(t[p*2].g, t[p*2+1].g);
  51.         t[p].Max = max(t[p*2].Max, t[p*2+1].Max);
  52.     }
  53.     int queryGcd(int p, int l, int r) {
  54.         if(t[p].l >= l && t[p].r <= r) return t[p].g;
  55.         int mid = t[p].l + t[p].r >> 1;
  56.         int g = 0;
  57.         if(l <= mid) g = gcd(g, queryGcd(p*2, l, r));
  58.         if(r > mid) g = gcd(g, queryGcd(p*2+1, l, r));
  59.         return g;
  60.     }
  61.     int queryMax(int p, int l, int r){
  62.         if(t[p].l >= l && t[p].r <= r) return t[p].Max;
  63.         int mid = t[p].l + t[p].r >> 1;
  64.         int Max = 0;
  65.         if(l <= mid) Max = max(Max, queryMax(p*2, l, r));
  66.         if(r > mid) Max = max(Max, queryMax(p*2+1, l, r));
  67.         return Max;
  68.     }
  69. }
  70. int main(){
  71.     scanf("%d%d", &n, &m);
  72.     for(int i=1;i<=n;i++) scanf("%d", &a[i]);
  73.     BIT::init(n);
  74.     for(int i=1;i<=n;i++) BIT::add(i, a[i] - a[i-1]);
  75.     SGT::init(n);
  76.     while(m--){
  77.         int op, l, r;
  78.         scanf("%d%d%d", &op, &l, &r);
  79.         if(op == 1) {
  80.             int x;scanf("%d", &x);
  81.             BIT::add(l, x);
  82.             if(r < n)
  83.                 BIT::add(r+1, -x);
  84.             SGT::change(1, l, x);
  85.             if(r < n)
  86.                 SGT::change(1, r+1, -x);
  87.         } else if(op == 2) {
  88.             if(l == r) puts("0");
  89.             else {
  90.                 printf("%d\n", SGT::queryMax(1, l+1, r));
  91.             }
  92.         } else {
  93.             printf("%d\n", gcd(BIT::query(l), abs(SGT::queryGcd(1, l+1, r))));
  94.         }
  95.     }
  96.     return 0;
  97. }