题号 标题 已通过代码 通过率 tag 难度
A 智乃的Hello XXXX 点击查看 3023/3257 签到 500
B 智乃买瓜 点击查看 1632/3604 DP 1300
C 智乃买瓜(another version) 点击查看 331/811 DP 1900
D 智乃的01串打乱 点击查看 2851/4923 模拟 1000
E 智乃的数字积木(easy version) 点击查看 829/1948 模拟 1400
F 智乃的数字积木(hard version) 点击查看 31/264 并查集启发式合并 2300
G 智乃的树旋转(easy version) 点击查看 438/1443 平衡树 1700
H 智乃的树旋转(hard version) 点击查看 77/179 平衡树 2000
I 智乃的密码 点击查看 746/4260 贪心模拟二分 1500
J 智乃的C语言模除方程 点击查看 109/861 数学 2000
K 智乃的C语言模除方程(another version) 点击查看 16/95 数学 2200
L 智乃的数据库 点击查看 1078/2757 模拟数据结构 1500

A

签到

B

分组背包DP模版题
设 d[i][j] 表示前 i 个西瓜，凑出重量 j 的方案数。
那么有动态转移方程：
第三场 01/28 - 图1
第 i 个瓜有三种转移策略：

  1. 不买，累加 第三场 01/28 - 图2
  2. 买半个，累加 第三场 01/28 - 图3
  3. 买一整个，累加第三场 01/28 - 图4

将这三个加到一起，就是 d[i][j] 了。
注意到，计算 d[i][j] 时，只会用到 d[i-1] 中更小的 j，所以可以使用滚动数组来压缩，倒序枚举 j 即可。（当然这一步省掉也是OK的）

  1. #include<bits/stdc++.h>
  2. using namespace std;
  3. #define rep(i,j,k) for(int i=int(j);i<=int(k);i++)
  4. #define per(i,j,k) for(int i=int(j);i>=int(k);i--)
  5. typedef long long ll;
  6. const int N = 1010, mod = 1e9 + 7;
  7. int n, m, w[N];
  8. ll d[N];
  9. int main(){
  10.   cin >> n >> m;
  11.   d[0] = 1;
  12.   rep(i,1,n) {
  13.     scanf("%d", &w[i]);
  14.     for(int j = m; j >= 0;j--){
  15.       if(j >= w[i]) d[j] = (d[j] + d[j - w[i]]) % mod;
  16.       if(j >= w[i] / 2) d[j] = (d[j] + d[j - w[i] / 2]) % mod;
  17.     }
  18.   }
  19.   rep(i,1,m) printf("%lld ", d[i]);
  20.   puts("");
  21. }

C

DP
由于只有买半个重量为 2 的西瓜，才有可能使得总重量为 1，所以 d[1] 就是西瓜重量为 2 的数量。
然后试图从 DP 数组中删除这些瓜的贡献：

  1. for(int t = 1; t <= d[1]; t ++){
  2.     for(int j = 1; j <= m; j ++) {
  3.         if(j >= w / 2) d[j] = (d[j] - d[j - 1] + mod) % mod;
  4.         if(j >= w) d[j] = (d[j] - d[j - 2] + mod) % mod;
  5.     }
  6. }

删除掉以后，当前 d[2] 的值就是西瓜重量为 4 的数量，然后再紧接着消除即可。

  1. #include<bits/stdc++.h>
  2. using namespace std;
  3. #define rep(i,j,k) for(int i=int(j);i<=int(k);i++)
  4. #define per(i,j,k) for(int i=int(j);i>=int(k);i--)
  5. typedef long long ll;
  6. const int N = 1010, mod = 1e9 + 7;
  7. int n, m, a[N], c[2 * N];
  8. ll d[N], f[N];
  10. int main(){
  11.   scanf("%d", &m);
  12.   rep(i,1,m) {
  13.     scanf("%lld", &d[i]);
  14.   }
  15.   d[0] = 1;
  16.   for(int i = 1; i <= m; i++){
  17.     int w = i * 2;
  18.     c[w] = d[i]; 
  19.     n += c[w];
  20.     for(int t = 1; t <= c[w]; t ++){
  21.       for(int j = 1; j <= m; j++){
  22.         if(j >= w / 2) d[j] = (d[j] - d[j - w / 2] + mod) % mod;
  23.         if(j >= w) d[j] = (d[j] - d[j - w] + mod) % mod;
  24.       }
  25.     }
  26.   }
  27.   printf("%d\n", n);
  28.   for(int i=2;i<=2*m;i+=2){
  29.     while(c[i]) {
  30.       printf("%d ", i);
  31.       c[i] --;
  32.     }
  33.   }
  34.   return 0;
  35. }

D

签到题
很简单，这里提供两种思路：

  1. 可以排序后与原串对比，如果不一样则输出，否则倒序之后输出。
  2. 找到随便一个与 s[0] 不同的字符，与之交换输出。 ```cpp

    include

    using namespace std;

    define rep(i,j,k) for(int i=int(j);i<=int(k);i++)

    define per(i,j,k) for(int i=int(j);i>=int(k);i—)

    typedef long long ll; int n; string s, t;

int main(){ cin >> n >> s; t = s; sort(s.begin(), s.end()); if(s != t) { cout << s << endl; } else{ reverse(s.begin(), s.end()); cout << s << endl; } return 0; }

  1. ```cpp
  2. #include <bits/stdc++.h>
  4. using i64 = long long;
  6. int main() {
  7.     std::ios::sync_with_stdio(false);
  8.     std::cin.tie(nullptr);
  10.     int n;
  11.     std::cin >> n;
  12.     std::string s;
  13.     std::cin >> s;
  15.     int x = s.find(s[0] ^ 1); // 由于字符中只有 '0'(ASCII 48) 和 '1' (ASCII 49)，所以可以通过异或来指定
  16.     std::swap(s[0], s[x]);
  17.     std::cout << s << "\n";
  19.     return 0;
  20. }

E

计算一个字符串表示的数字取模后的值：

  1. string s;
  2. cin >> s;
  3. long long rs = 0;
  4. for(auto &c : s) {
  5.     rs = (rs * 10 + c - '0') % mod;
  6. }
  7. cout << rs << endl;

对于原串中颜色相同的一个区间 [l, r]（用双指针维护一下），然后对 [l, r] 按照降序排列，最后计算即可。

  1. #include<bits/stdc++.h>
  2. using namespace std;
  3. #define rep(i,j,k) for(int i=int(j);i<=int(k);i++)
  4. #define per(i,j,k) for(int i=int(j);i>=int(k);i--)
  5. typedef long long ll;
  6. const int N = 100010, mod = 1e9 + 7;
  7. int n, m, k;
  8. char s[N], t[N];
  9. int c[N];
  10. int get() {
  11.   memcpy(t, s, sizeof t);
  12.   int l = 1;
  13.   rep(i, 1, n) {
  14.     // 当 i == n 或 i 和 i + 1 颜色不同时，i 为区间右端点
  15.     if(i == n || c[i] != c[i + 1]) {
  16.       sort(t + l, t + i + 1, greater<char>()); // 对 [l, i] 降序排序
  17.       l = i + 1; // 设置新的区间左端点
  18.     }
  19.   }
  20.   ll sum = 0;
  21.   rep(i,1,n) {
  22.     sum = sum * 10 + (t[i] - '0');
  23.     sum %= mod;
  24.   }
  25.   return sum;
  26. }
  27. int main(){
  28.   scanf("%d%d%d", &n, &m, &k);
  29.   scanf("%s", s + 1);
  30.   rep(i,1,n) {
  31.     scanf("%d", &c[i]);
  32.   }
  33.   printf("%d\n", get());
  34.   while(k--){
  35.     int x, y;
  36.     scanf("%d%d", &x, &y);
  37.     rep(i,1,n) if(c[i] == x) c[i] = y; // 修改颜色
  38.     printf("%d\n", get());
  39.   }
  40.   return 0;
  41. }

F

题意与E题相同，不同的是变色次数变成了 第三场 01/28 - 图5。

样例： 字符：12345 初试颜色：1 2 3 4 3

每个颜色分配一个集合：
颜色1：[1, 1]
颜色2：[2, 2]
颜色3：[3, 3]，[5, 5]
颜色4：[4, 4]
每种颜色对应一个集合，集合中包含若干区间，每个区间的颜色都应当统一。
当颜色 x 和染成颜色 y 时，等同于将集合 x 中的元素移动到集合 y 中，并对集合 y 中的区间进行合并。
我们每次将小的集合向大的集合合并，这样的操作，总体复杂度为 第三场 01/28 - 图6，因为每次合并，集合大小至少扩大二倍，所以最终每个元素的合并次数不超过 第三场 01/28 - 图7。
具体合并时，假设 x 是较小的集合，遍历其中的每个区间，尝试与 y 中与之相邻的区间进行合并（使用 lower_bound等二分快速找到相邻集合）。
我们可以用一个结构体来描述一个区间：

  1. struct Node {
  2.   int l, r; // 区间左右端点
  3.   int cnt[10]; // cnt[x] 表示该区间中 x 的个数
  4.   ll sum; // 该区间对整体答案的贡献
  5.   Node(){ // 构造函数，初始化
  6.     l = r = sum = 0;
  7.     memset(cnt, 0, sizeof cnt);
  8.   }
  9.   void get(){ // 更新该区间对最终答案的贡献
  10.     sum = 0;
  11.     int suf = n - l + 1; // suf 为当前区间所处的后缀长度
  12.     for(int i = 9; i >= 0; i--){ // 贪心的，优先考虑拼凑最大的，从9开始倒序考虑
  13.       // 这里要拼凑 cnt[i] 个 i，可以用 10^cnt[i] - 1 来表示 cnt[i] 个 9 的数值，然后除以 9 再乘 i
  14.       // 比如 5 个 4 即 44444 等于 (10^5 - 1) / 9 * 4 = 99999 / 9 * 4
  15.       // 模意义下，除法要变为乘逆元
  16.       // 最后还要乘上 10^suf
  17.       suf -= cnt[i];
  18.       // (10^cnt - 1) / 9 * k
  19.       sum = (sum + (P[cnt[i]] - 1 + mod) % mod * inv9 % mod * i % mod * P[suf] % mod) % mod;
  20.     }
  21.   }
  22.   // 重载 < 运算符，用于二分查找
  23.   bool operator < (const Node & o) const {
  24.     return l < o.l;
  25.   }
  26. };

因此，可以方便的实现集合合并，顺便进行最终答案的修改。由于启发式合并以及单次合并要进行二分查找，所以总体复杂度为第三场 01/28 - 图8。

  1. #include<bits/stdc++.h>
  2. using namespace std;
  3. #define dbg(x...) do { cout << "\033[32;1m" << #x <<" -> "; err(x); } while (0)
  4. void err() { cout << "\033[39;0m" << endl; }
  5. template<class T, class... Ts> void err(const T& arg,const Ts&... args) { cout << arg << " "; err(args...); }
  6. #define rep(i,j,k) for(int i=int(j);i<=int(k);i++)
  7. #define per(i,j,k) for(int i=int(j);i>=int(k);i--)
  8. typedef long long ll;
  9. const int N = 100010, mod = 1e9 + 7;
  10. int n, m, k, col[N];
  11. ll P[N], inv9, rs;
  12. ll ksm(ll a, ll b){
  13.   ll rs = 1;
  14.   for(;b;b >>= 1) {
  15.     if(b & 1) rs = rs * a % mod;
  16.     a = a * a % mod;
  17.   }
  18.   return rs;
  19. }
  20. char s[N];
  21. struct Node {
  22.   int l, r;
  23.   int cnt[10];
  24.   ll sum;
  25.   Node(){
  26.     l = r = sum = 0;
  27.     memset(cnt, 0, sizeof cnt);
  28.   }
  29.   void get(){
  30.     sum = 0;
  31.     int suf = n - l + 1;
  32.     for(int i = 9; i >= 0; i--){
  33.       suf -= cnt[i];
  34.       sum = (sum + (P[cnt[i]] - 1 + mod) % mod * inv9 % mod * i % mod * P[suf] % mod) % mod;
  35.     }
  36.   }
  37.   bool operator < (const Node & o) const {
  38.     return l < o.l;
  39.   }
  40. };
  41. set<Node> st[N];
  42. void get(){
  43.   Node t; 
  44.   t.l = 1; t.sum = 0;
  45.   rep(i,1,n) {
  46.     t.cnt[s[i] - '0'] ++;
  47.     if(i == n || col[i] != col[i + 1]) {
  48.       t.r = i;
  49.       t.get();
  50.       rs = (rs + t.sum) % mod;
  51.       st[col[i]].insert(t);
  52.       t.l = i + 1;
  53.       memset(t.cnt, 0, sizeof t.cnt);
  54.     }
  55.   }
  56. }
  58. void merge(int x, int y){
  59.   if(st[x].size() < st[y].size()) {
  60.     swap(st[x], st[y]);
  61.   }
  62.   // 集合合并
  63.   for(auto t : st[y]) {
  64.     auto it = st[x].upper_bound(t);
  65.     if(it != st[x].end() && (*it).l == t.r + 1) {
  66.       Node p = *it;
  67.       st[x].erase(it);
  68.       rs = (rs - t.sum + mod - p.sum + mod) % mod;
  69.       for(int i = 9; i >= 0; i--) t.cnt[i] += p.cnt[i];
  70.       t.r = p.r;
  71.       t.get();
  72.       rs = (rs + t.sum) % mod;
  73.     }
  74.     it = st[x].lower_bound(t);
  75.     if(it != st[x].begin() && ((*--it).r == t.l - 1)) {
  76.       Node p = *it;
  77.       st[x].erase(it);
  78.       rs = (rs - t.sum + mod - p.sum + mod) % mod;
  79.       for(int i = 9; i >= 0; i--) t.cnt[i] += p.cnt[i];
  80.       t.l = p.l;
  81.       t.get();
  82.       rs = (rs + t.sum) % mod;
  83.     }
  84.     st[x].insert(t);
  85.   }
  86.   swap(st[x], st[y]);
  87.   st[x].clear();
  88. }
  89. int main(){
  90.   scanf("%d%d%d", &n, &m, &k);
  91.   scanf("%s", s + 1);
  93.   P[0] = 1;
  94.   rep(i,1,n) P[i] = P[i-1] * 10 % mod;
  95.   inv9 = ksm(9, mod - 2);
  97.   rep(i,1,n) {
  98.     scanf("%d", &col[i]);
  99.   }
  100.   get();
  101.   printf("%lld\n", rs);
  102.   while(k --){
  103.     int x, y; scanf("%d%d", &x, &y);
  104.     if(x != y) merge(x, y);
  105.     printf("%lld\n", rs);
  106.   }
  107. }

G

image.png
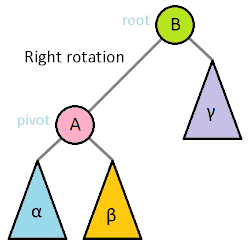
A 要进行右旋，旋转后 A 将变为 B 的父亲，假设实际树中 B 还有父亲 C，那么 C 的孩子将有原来的 B 替换为 A。
所以，给定两个树 A，B，如果只进行了最多一次旋转，我们只需要同时从两个树的根开始 DFS，如果遇到某个结点 X，X 在 A 树中的左孩子（或右孩子）是 H，而 X 在 B 树中的左孩子（或右孩子）是 G，那么说明是 G 进行了旋转。

  1. #include<bits/stdc++.h>
  2. using namespace std;
  3. #define rep(i,j,k) for(int i=int(j);i<=int(k);i++)
  4. #define per(i,j,k) for(int i=int(j);i>=int(k);i--)
  5. typedef long long ll;
  6. const int N = 1010;
  7. int n;
  8. bool flag;
  9. struct Tr{
  10.   int l[N], r[N];
  11.   int fa[N];
  12.   int rt;
  13.   // 初始化 fa 数组 和 rt（即 root）
  14.   void getf(){
  15.     rep(i,1,n) {
  16.       fa[l[i]] = i;
  17.       fa[r[i]] = i;
  18.     }
  19.     rep(i,1,n) {
  20.       if(fa[i] == 0) rt = i;
  21.     }
  22.   }
  23. }A, B;
  24. void dfs(int x) {
  25.   if(x == 0) return; // 为 0 直接返回，否则会无限递归
  26.   if(flag) return;  
  27.   if(A.l[x] == B.l[x]) {
  28.     dfs(A.l[x]);
  29.   } else { // 左孩子不同
  30.     printf("%d\n", A.l[x]);
  31.     flag = true; return;
  32.   }
  33.   if(A.r[x] == B.r[x]) { // 右孩子不同
  34.     dfs(A.r[x]);
  35.   } else {
  36.     printf("%d\n", A.r[x]);
  37.     flag = true; return;
  38.   }
  39. }
  40. int main(){
  41.   scanf("%d", &n);
  42.   rep(i,1,n) {
  43.     scanf("%d%d", &A.l[i], &A.r[i]);
  44.   }
  45.   A.getf();
  46.   rep(i,1,n) {
  47.     scanf("%d%d", &B.l[i], &B.r[i]);
  48.   }
  49.   B.getf();
  50.   bool fg = false;
  51.   // 判断两个树是否一致
  52.   rep(i,1,n) {
  53.     if(A.l[i] == B.l[i] && A.r[i] == B.r[i]) continue;
  54.     fg = true; break;
  55.   }
  56.   if(!fg) {
  57.     printf("0\n");
  58.     return 0;
  59.   }
  60.   printf("1\n");
  61.   if(A.rt != B.rt) { 
  62.     printf("%d\n", A.rt);
  63.     return 0;
  64.   }
  65.   dfs(A.rt);
  66.   return 0;
  67. }

H

有两个树A，B。我们要对 B 进行复原成A。
第一步可以做的就是，判断 A 和 B 的根是否一致。
如果不一致，设 X 为 A 当前的根，在 B 中找到 X，然后将 X 向上旋转，直到 X 为当前的根。（实际处理过程要注意细节）
如果一致则分别递归左右两边。
递归后，当做子树问题来处理即可。根据二叉搜索树的性质，根结点如果一致，那么两边的结点集合也一定是相同的。
难点在于代码上。

  1. #include<bits/stdc++.h>
  2. using namespace std;
  3. #define dbg(x...) do { cout << "\033[32;1m" << #x <<" -> "; err(x); } while (0)
  4. void err() { cout << "\033[39;0m" << endl; }
  5. template<class T, class... Ts> void err(const T& arg,const Ts&... args) { cout << arg << " "; err(args...); }
  6. #define rep(i,j,k) for(int i=int(j);i<=int(k);i++)
  7. #define per(i,j,k) for(int i=int(j);i>=int(k);i--)
  8. typedef long long ll;
  9. const int N = 1010;
  10. int n;
  11. bool flag;
  12. struct Tr{
  13.   int l[N], r[N];
  14.   int fa[N];
  15.   int rt;
  16.   void getf(){
  17.     rep(i,1,n) {
  18.       fa[l[i]] = i;
  19.       fa[r[i]] = i;
  20.     }
  21.     rep(i,1,n) {
  22.       if(fa[i] == 0) {
  23.         rt = i;
  24.         l[0] = rt;
  25.       }
  26.     }
  27.   }
  28.   void rotate(int p) {
  29.     // 旋转代码不要写错，除了维护 l,r 还要维护 fa
  30.     int f = fa[p], anc = fa[f];
  31.     if(p == l[f]) { // 右旋
  32.       int rson = r[p];
  33.       l[f] = rson; fa[rson] = f;
  34.       r[p] = f; fa[f] = p;
  35.       if(f == l[anc]) l[anc] = p;
  36.       else r[anc] = p;
  37.       fa[p] = anc;
  38.     } else { // 左旋
  39.       int lson = l[p];
  40.       r[f] = lson; fa[lson] = f;
  41.       l[p] = f; fa[f] = p;
  42.       if(f == l[anc]) l[anc] = p;
  43.       else r[anc] = p;
  44.       fa[p] = anc;
  45.     }
  46.     rt = l[0];
  47.   }
  48. }A, B;
  49. vector<int> rs;
  50. void dfs(int Art, int Brt) {
  51.   if(Art == 0) return;
  52.   // 如果当前子树中，A的根和B的根不一致，那么就要对B进行调整
  53.   if(Art != Brt){
  54.     // 不断的调整 B 中 Art 的位置，使得 Art 在A 和 B 中的父亲是一致的（也就是子树的根一致了）
  55.     while(A.fa[Art] != B.fa[Art]) {
  56.       B.rotate(Art);
  57.       rs.push_back(Art);
  58.     }
  59.   }
  60.   dfs(A.l[Art], B.l[Art]);
  61.   dfs(A.r[Art], B.r[Art]);
  62. }
  63. int main(){
  64.   scanf("%d", &n);
  65.   rep(i,1,n) {
  66.     scanf("%d%d", &A.l[i], &A.r[i]);
  67.   }
  68.   A.getf();
  69.   rep(i,1,n) {
  70.     scanf("%d%d", &B.l[i], &B.r[i]);
  71.   }
  72.   B.getf();
  73.   bool fg = false;
  74.   rep(i,1,n) {
  75.     if(A.l[i] == B.l[i] && A.r[i] == B.r[i]) continue;
  76.     fg = true; break;
  77.   }
  78.   if(!fg) {
  79.     printf("0\n");
  80.     return 0;
  81.   }
  82.   dfs(A.rt, B.rt);
  83.   printf("%d\n", (int) rs.size());
  84.   for(auto &x : rs) printf("%d ", x);
  85.   return 0;
  86. }

I

首先判断得到每个字符它所属的类别，然后用前缀和 d[i][j] 表示前面 i 个字符中，类别 j 的个数。
假设 [L, R] 满足要求，那么对于所有的 l < L, [l, R] 都满足要求。
固定 R，求解最大的 L，使得 [L, R] 满足要求。然后考虑 R 递增，这样的 L 也是非严格递增的，所以可以用一个指针来维护 L。
每次求到的都是最短的区间 [L, R], 所以符合要求的长度区间为 [R - L + 1, R], 与题目输入的区间求交即可。
当然，L 也可以每次二分去求。
7ms

  1. #include<bits/stdc++.h>
  2. using namespace std;
  3. #define dbg(x...) do { cout << "\033[32;1m" << #x <<" -> "; err(x); } while (0)
  4. void err() { cout << "\033[39;0m" << endl; }
  5. template<class T, class... Ts> void err(const T& arg,const Ts&... args) { cout << arg << " "; err(args...); }
  6. #define rep(i,j,k) for(int i=int(j);i<=int(k);i++)
  7. #define per(i,j,k) for(int i=int(j);i>=int(k);i--)
  8. typedef long long ll;
  9. const int N = 100010;
  10. int n, l, r;
  11. char s[N];
  12. int d[N][4];
  13. int get(int L, int R) {
  14.   return max(0, min(R, r) - max(L, l) + 1); 
  15. }
  16. bool check(int L, int R) {
  17.   int cnt = 0;
  18.   rep(i,0,3) if(d[R][i] - d[L - 1][i] > 0) cnt ++;
  19.   return cnt >= 3;
  20. }
  21. int main(){
  22.   cin >> n >> l >> r;
  23.   scanf("%s", s + 1);
  24.   ll rs = 0;
  25.   int L = 1;
  26.   rep(i,1,n) {
  27.     int t;
  28.     if(s[i] >= 'a' && s[i] <= 'z') t = 0;
  29.     else if(s[i] >= 'A' && s[i] <= 'Z') t = 1;
  30.     else if(s[i] >= '0' && s[i] <= '9') t = 2;
  31.     else t = 3;
  32.     // memcpy 内存拷贝，直接赋值之前的
  33.     memcpy(d[i], d[i-1], sizeof d[i]);
  34.     d[i][t] ++;
  35.     // 贪心，尽量让 L 变得更大
  36.     while(L < i && check(L + 1, i)) L++;
  37.     if(check(L, i)) {
  38.       rs += get(i - L + 1, i); // [i - L + 1, i] 与 [l, r] 求交
  39.     }
  40.   }
  41.   printf("%lld\n", rs);
  42.   return 0;
  43. }

二分（12ms）：

  1. #include<bits/stdc++.h>
  2. using namespace std;
  3. #define dbg(x...) do { cout << "\033[32;1m" << #x <<" -> "; err(x); } while (0)
  4. void err() { cout << "\033[39;0m" << endl; }
  5. template<class T, class... Ts> void err(const T& arg,const Ts&... args) { cout << arg << " "; err(args...); }
  6. #define rep(i,j,k) for(int i=int(j);i<=int(k);i++)
  7. #define per(i,j,k) for(int i=int(j);i>=int(k);i--)
  8. typedef long long ll;
  9. const int N = 100010;
  10. int n, l, r;
  11. char s[N];
  12. int d[N][4];
  13. int get(int L, int R) {
  14.   return max(0, min(R, r) - max(L, l) + 1); 
  15. }
  16. int main(){
  17.   cin >> n >> l >> r;
  18.   scanf("%s", s + 1);
  19.   ll rs = 0;
  20.   rep(i,1,n) {
  21.     int t;
  22.     if(s[i] >= 'a' && s[i] <= 'z') t = 0;
  23.     else if(s[i] >= 'A' && s[i] <= 'Z') t = 1;
  24.     else if(s[i] >= '0' && s[i] <= '9') t = 2;
  25.     else t = 3;
  26.     memcpy(d[i], d[i-1], sizeof d[i]);
  27.     d[i][t] ++;
  28.     int L = -1, R = i - 1;
  29.     while(L < R) {
  30.       int m = L + R + 1 >> 1;
  31.       int mn = 0;
  32.       rep(j,0,3) mn += d[i][j] - d[m][j] > 0;
  33.       if(mn >= 3) {
  34.         L = m;
  35.       } else R = m - 1;
  36.     }
  37.     if(L != -1) {
  38.       rs += get(i - L, i);
  39.     }
  40.   }
  41.   printf("%lld\n", rs);
  42.   return 0;
  43. }

J

第三场 01/28 - 图10，问有多少 x，满足第三场 01/28 - 图11
第三场 01/28 - 图12
题目中有说，取模后的结果，正负号与 P 无关，只与 x 有关。所以一开始我们就可以将 P 直接取绝对值。
对于 [L,R] 和 [l,r]，区间内可能正负数都有，但我们可以将负数对称过来当正数处理。
对于原本正数的部分：[ max(0, L), R] 和 [ max(0, l), r]
对于原本负数的部分：[max(0, -R), -L] 和 [max(0, -r), -l]
当然，如果 R < 0, 那么 [ max(0, L), R] 就是个不正确的区间，区间右端点小于左端点的特殊情况，可以直接返回 0 的结果。
然后，按照上面的分类，进行正数和负数部分计算时，0会被计算两次，所以可以将负数部分整体右移：[max(1, -R), -L] 和 [max(0, -r), -l]（值域并不右移）

所以，现在问题简化为：第三场 01/28 - 图13
设 get(R, r) 表示有多少 0 <= x <= R 模 P 后 Q 满足 0 <= Q <= r。
那么直接调用 (get(R, r) - get(R, l - 1)) - (get(L - 1, r) - get(L - 1, l - 1)) 即可。
get(R, r) 如何实现，留给自己想象。

  1. int p, l, r, L, R;
  2. ll rs;
  3. int get(int R, int r) {
  4.   if(R < 0 || r < 0) return 0;
  5.   r = min(r, p - 1);
  6.   return R / p * (r + 1) + min(R % p, r) + 1;
  7. }
  8. int get(int L, int R, int l, int r) {
  9.   if(R < L || r < l) return 0;
  10.   return (get(R, r) - get(R, l - 1)) - (get(L - 1, r) - get(L - 1, l - 1));
  11. }
  12. int main(){
  13.   cin >> p >> l >> r >> L >> R;
  14.   p = abs(p);
  15.   int rs = get(max(0, L), R, max(0, l), r)
  16.           + get(max(1, -R), -L, max(0, -r), -l);
  17.   printf("%d\n", rs);
  18.   return 0;
  19. }

K

第三场 01/28 - 图14，问有多少 x，满足第三场 01/28 - 图15
找不到切入点时，可以尝试打表找规律。下面是给出定理和证明：
如果有两个整数 第三场 01/28 - 图16
由取模定义：第三场 01/28 - 图17
可以得到：第三场 01/28 - 图18
所以，如果有一个数列：第三场 01/28 - 图19，其取值第三场 01/28 - 图20 相同。那么 第三场 01/28 - 图21 是一个等差数列。

例如，100 / 34 = 100 / 50 = 2，所以对于 {34, 35, 36, … 50}，取模后构成等差数列： 100 % 34 = 32, 100 % 35 = 30, 100 % 36 = 28, … 100 % 50 = 0

所以，如果要求 [1, R] 中有多少 x 满足 P % x 在 [0, r] 范围内，可以使用数论分块快速计算。（即每一块内，构成一个等差数列）
其余的部分与 J 题类似。

  1. const int inf = 1e9 + 3;
  2. int p, l, r, L, R;
  4. int get(int R, int r) {
  5.   if(R < 1 || r < 0) return 0;
  6.   int rs = 0;
  7.   // 对于 R > p 的情况，p % x 恒等于 p，单独统计答案
  8.   if(R > p) {
  9.     if(r >= p) rs += R - p;
  10.     R = p;
  11.   }
  12.   // 数论分块，复杂度 O(根号R)
  13.   for(int x = 1, y = 0; x <= R; x = y + 1) {
  14.     //定义 k = p / x，那么 [x, y] 中的所有值 i 都有 p / i  = k，且 y 是满足这个条件的最大值，x是最小值。
  15.     y = min(R, p / (p / x));
  16.     // s 为等差数列首项，t 为末项
  17.     int s = p % y, t = p % x;
  18.     int cnt = y - x + 1;
  19.     // 计算等差数列中有多少数字在 [0, r] 中
  20.     if(t <= r) rs += cnt;
  21.     else if(s <= r) {
  22.       int d = (t - s) / (y - x);
  23.       rs += (r - s) / d + 1;
  24.     }
  25.   }
  26.   return rs;
  27. }
  29. int get(int L, int R, int l, int r) {
  30.   if(L > R || l > r) return 0;
  31.   return get(R, r) - get(R, l - 1) - get(L - 1, r) + get(L - 1, l - 1);
  32. }
  33. int main(){
  34.   cin >> p >> l >> r >> L >> R;
  35.   // 将 p < 0 的情况对称到 p >= 0, 值域 [l,r] 也要相应翻转
  36.   if(p < 0) {
  37.     p = -p;
  38.     l = -l, r = -r;
  39.     swap(l, r);
  40.   }
  41.   // 由于 p >= 0，所以 l >= 0 的情况才会被计算
  42.   l = max(0, l);
  43.   int rs = get(max(1, L), R, l, r)
  44.           + get(max(1, -R), -L, l, r);
  45.   printf("%d\n", rs);
  46. }

L

序列去重、计数问题。
难点：从输入的SQL语句中提取出关键字，然后筛选出目标列。序列计数操作。
可以直接用 map, int> 来计数，也可以对 vector 排序后比较计算。
直接用 map 166 ms

  1. #include<bits/stdc++.h>
  2. using namespace std;
  3. #define rep(i,j,k) for(int i=int(j);i<=int(k);i++)
  4. #define per(i,j,k) for(int i=int(j);i>=int(k);i--)
  5. typedef long long ll;
  6. const int N = 1010;
  7. int n, m;
  8. string s[N], q;
  9. int a[N][N];
  10. vector<int> v;
  11. unordered_map<string,int> mp;
  12. vector<vector<int>> b;
  13. map<vector<int>, int> mp2;
  14. vector<int> rs;
  15. int main(){
  16.   scanf("%d%d", &n, &m);
  17.   rep(i,1,m) cin >> s[i], mp[s[i]] = i;
  18.   rep(i,1,n) rep(j,1,m) scanf("%d", &a[i][j]);
  19.   getline(cin, q); // 读取空行
  20.   getline(cin, q); // 读取 SQL
  21.   q = q.substr(36);
  22.   q.pop_back(); // 将最后的分号去掉
  23.   int i = 0;
  24.   while(i < q.size()) {
  25.     int j = q.find(',', i); // 获得下一个 ',' 的位置
  26.     if(j == -1) j = q.size(); // 如果没有，直接定位到最后
  27.     string t = q.substr(i, j - i); // 获得子串 term
  28.     v.push_back(mp[t]);
  29.     i = j + 1;
  30.   }
  31.   rep(i,1,n) {
  32.     vector<int> t;
  33.     for(auto &x : v) {
  34.       t.push_back(a[i][x]);
  35.     }
  36.     mp2[t] ++;
  37.   }
  38.   printf("%d\n",(int) mp2.size());
  39.   for(auto [k, v] : mp2) { 
  40.     printf("%d ", v);
  41.   }
  42.   puts("");
  43.   return 0;
  44. }

对 vector 排序，130ms

  1. #include<bits/stdc++.h>
  2. using namespace std;
  3. #define rep(i,j,k) for(int i=int(j);i<=int(k);i++)
  4. #define per(i,j,k) for(int i=int(j);i>=int(k);i--)
  5. typedef long long ll;
  6. const int N = 1010;
  7. int n, m;
  8. string s[N], q;
  9. int a[N][N];
  10. vector<int> v;
  11. unordered_map<string,int> mp;
  12. vector<vector<int>> b;
  13. vector<int> rs;
  14. int main(){
  15.   scanf("%d%d", &n, &m);
  16.   rep(i,1,m) cin >> s[i], mp[s[i]] = i;
  17.   rep(i,1,n) rep(j,1,m) scanf("%d", &a[i][j]);
  18.   getline(cin, q);
  19.   getline(cin, q);
  20.   q = q.substr(36);
  21.   q.pop_back();
  22.   int i = 0;
  23.   while(i < q.size()) {
  24.     int j = q.find(',', i);
  25.     if(j == -1) j = q.size();
  26.     string t = q.substr(i, j - i);
  27.     v.push_back(mp[t]);
  28.     i = j + 1;
  29.   }
  30.   rep(i,1,n) {
  31.     vector<int> t;
  32.     for(auto &x : v) {
  33.       t.push_back(a[i][x]);
  34.     }
  35.     b.push_back(t);
  36.   }
  37.   // 排序
  38.   sort(b.begin(), b.end());
  39.   for(int i = 0; i < b.size(); i++){
  40.     if(i == 0 || b[i] != b[i-1]) { // 与前面的不一样，则新增一个 1
  41.       rs.push_back(1);
  42.     } else { // 一样则 ++
  43.       rs[rs.size() - 1] ++;
  44.     }
  45.   }
  46.   cout << rs.size() << endl;
  47.   for(auto &x : rs) printf("%d ", x);
  48.   puts("");
  49.   return 0;
  50. }