防晒

有 0x07 贪心 - 图1 头奶牛进行日光浴，第 0x07 贪心 - 图2 头奶牛需要 0x07 贪心 - 图3 到 0x07 贪心 - 图4 单位强度之间的阳光。
每头奶牛在日光浴前必须涂防晒霜，防晒霜有 0x07 贪心 - 图5 种，涂上第 0x07 贪心 - 图6 种之后，身体接收到的阳光强度就会稳定为 0x07 贪心 - 图7，第 0x07 贪心 - 图8 种防晒霜有 0x07 贪心 - 图9 瓶。
求最多可以满足多少头奶牛进行日光浴。
输入格式
第一行输入整数 0x07 贪心 - 图10 和 0x07 贪心 - 图11。
接下来的 0x07 贪心 - 图12 行，按次序每行输入一头牛的 0x07 贪心 - 图13 和 0x07 贪心 - 图14 值，即第 0x07 贪心 - 图15 行输入 0x07 贪心 - 图16 和 0x07 贪心 - 图17。
再接下来的 0x07 贪心 - 图18 行，按次序每行输入一种防晒霜的 0x07 贪心 - 图19 和 0x07 贪心 - 图20 值，即第 0x07 贪心 - 图21 行输入 0x07 贪心 - 图22 和 0x07 贪心 - 图23。
每行的数据之间用空格隔开。
输出格式
输出一个整数，代表最多可以满足奶牛日光浴的奶牛数目。
数据范围
0x07 贪心 - 图24,
0x07 贪心 - 图25,
0x07 贪心 - 图26
输入样例：

  1. 3 2
  2. 3 10
  3. 2 5
  4. 1 5
  5. 6 2
  6. 4 1

输出样例：

  1. 2

Point 1观察数据范围，可以接受 0x07 贪心 - 图27级别的方法。尝试对牛按照 0x07 贪心 - 图28排序。那么应该按照什么排序规则呢？ Point 2为了达到最大值，我们需要保证每个防晒霜都用的很有价值，即不能浪费。
我们用 0x07 贪心 - 图29来称呼牛的区间。

  1. 如果按照从 0x07 贪心 - 图30从小到大排序，那么如果当前我们找到两个防晒霜 0x07 贪心 - 图31满足 0x07 贪心 - 图32可以满足当前牛，思考 0x07 贪心 - 图33对于后面的牛是什么情况？
  2. 如果按照从 0x07 贪心 - 图34从小到大排序呢？ Point 3
  3. 如果按照 0x07 贪心 - 图35从小到大排序:
    • x, y 都不符合
    • x 符合，y 不符合
    • x 不符合，y 符合

所以，不论我们当前选择 x 还是选择 y，都不能保证最优。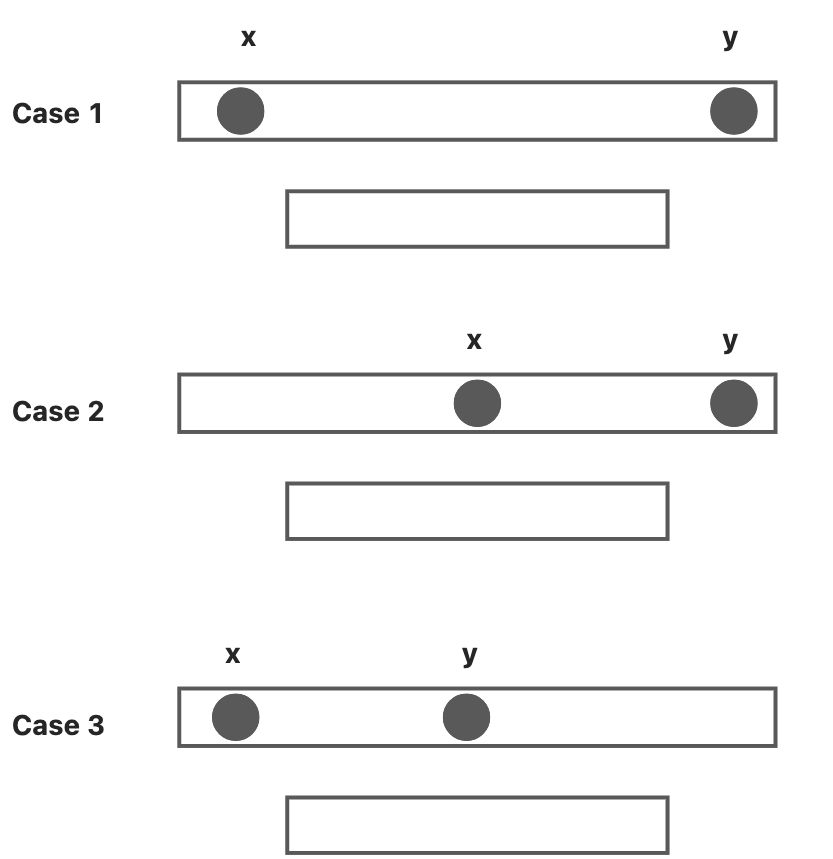
0x07 贪心 - 图36

  1. 如果按照 0x07 贪心 - 图37从小到大排序：
    • x 不符合，y 符合
    • x，y 都不符合
    • x，y 都符合

所以，在这种情况中，我们可以选择 x，把 y 留给后面。因为每个防晒霜只能服务一个牛，所以贪心
的选择 x 是更优的。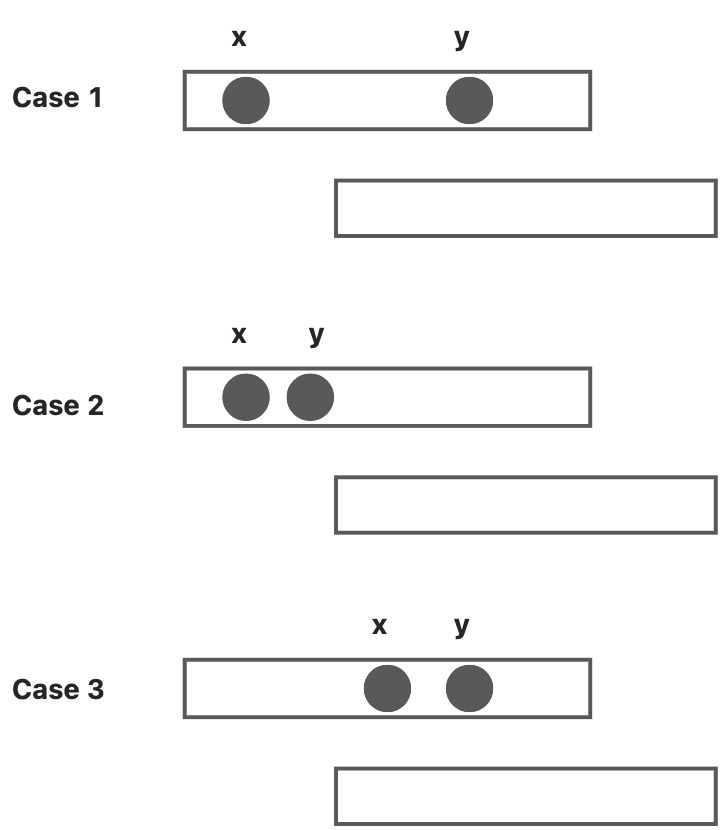
0x07 贪心 - 图38
所以，按照右端点从小到大排序，右端点相同则按照左端点从小到大排序。
依次遍历每头奶牛，去寻找所有满足该牛要求的防晒霜中SPF值最小的哪一个。

  1. #include <bits/stdc++.h>
  2. using namespace std;
  3. struct node{
  4.     int mi;
  5.     int mx;
  6. }a[3000];
  7. int C,L;
  8. struct SPF{
  9.     int num;
  10.     int spf;
  11. }s[3000];
  12. bool cmp(node a,node b){
  13.     if(a.mx==b.mx)
  14.         return a.mi<b.mi;
  15.     return a.mx<b.mx;
  16. }
  17. bool cmp2(SPF a,SPF b){
  18.     return a.spf<b.spf;
  19. }
  20. int main(){
  21.     scanf("%d%d",&C,&L);
  22.     for(int i=0;i<C;i++)
  23.         scanf("%d%d",&a[i].mi,&a[i].mx);
  24.     for(int i=0;i<L;i++)
  25.         scanf("%d%d",&s[i].spf,&s[i].num);
  26.     sort(a,a+C,cmp);
  27.     sort(s,s+L,cmp2);
  28.     int ans = 0;
  29.     for(int i=0;i<C;i++){
  30.         for(int j=0;j<L;j++){
  31.             if(s[j].spf>=a[i].mi&&s[j].spf<=a[i].mx&&s[j].num>0){
  32.                 s[j].num--;
  33.                 ans++;
  34.                 break;
  35.             }
  36.         }
  37.     }
  38.     cout<<ans<<endl;
  39.     return 0;
  40. }

畜栏预定

有 0x07 贪心 - 图39 头牛在畜栏中吃草。
每个畜栏在同一时间段只能提供给一头牛吃草，所以可能会需要多个畜栏。
给定 0x07 贪心 - 图40 头牛和每头牛开始吃草的时间 0x07 贪心 - 图41 以及结束吃草的时间 0x07 贪心 - 图42，每头牛在 0x07 贪心 - 图43 这一时间段内都会一直吃草。
当两头牛的吃草区间存在交集时（包括端点），这两头牛不能被安排在同一个畜栏吃草。
求需要的最小畜栏数目和每头牛对应的畜栏方案。
输入格式
第 0x07 贪心 - 图44 行：输入一个整数 0x07 贪心 - 图45。
第 0x07 贪心 - 图46 行：第 0x07 贪心 - 图47 行输入第 0x07 贪心 - 图48 头牛的开始吃草时间 0x07 贪心 - 图49 以及结束吃草时间 0x07 贪心 - 图50，数之间用空格隔开。
输出格式
第 0x07 贪心 - 图51 行：输入一个整数，代表所需最小畜栏数。
第 0x07 贪心 - 图52 行：第 0x07 贪心 - 图53 行输入第 0x07 贪心 - 图54 头牛被安排到的畜栏编号，编号是从 0x07 贪心 - 图55 开始的 连续 整数，只要方案合法即可。
数据范围
0x07 贪心 - 图56,
0x07 贪心 - 图57
输入样例：

  1. 5
  2. 1 10
  3. 2 4
  4. 3 6
  5. 5 8
  6. 4 7

输出样例：

  1. 4
  2. 1
  3. 2
  4. 3
  5. 2
  6. 4

将区间按照左端点从小到大排序，左端点相同则按照右端点排序。
用优先队列维护当前每个蓄栏结束使用的时间，对于每个区间，若最小结束使用的蓄栏可供当前区间使用，则修改后继续放入优先队列，否则直接在优先队列中添加一个新的元素。

  1. #include<bits/stdc++.h>
  2. using namespace std;
  3. #define dbg(x...) do { cout << "\033[32;1m" << #x <<" -> "; err(x); } while (0)
  4. void err() { cout << "\033[39;0m" << endl; }
  5. template<class T, class... Ts> void err(const T& arg,const Ts&... args) { cout << arg << " "; err(args...); }
  6. #define rep(i,j,k) for(int i=int(j);i<=int(k);i++)
  7. #define per(i,j,k) for(int i=int(j);i>=int(k);i--)
  8. typedef long long ll;
  9. const int N = 50005;
  10. using PII = pair<int, int>;
  11. int n, b[N];
  12. struct Cow {
  13.     int l, r, id;
  14.     bool operator < (const Cow & rth)const  {
  15.         return l < rth.l;
  16.     }
  17. };
  19. Cow a[N];
  21. int main(){
  22.     ios::sync_with_stdio(false); cin.tie(nullptr);
  23.     cin >> n;
  24.     for(int i = 1; i <= n; i++) {
  25.         cin >> a[i].l >> a[i].r;
  26.         a[i].id = i;
  27.     }
  29.     sort(a + 1, a + n + 1);
  30.     priority_queue<PII, vector<PII>, greater<PII>> q;
  31.     for(int i = 1; i <= n; i++) {
  32.         int l = a[i].l, r = a[i].r, id = a[i].id;
  33.         if(q.size() == 0 || q.top().first > l) {
  34.             b[id] = q.size() + 1;
  35.             q.push({r + 1, b[id]});
  36.         } else {
  37.             b[id] = q.top().second; q.pop();
  38.             q.push({r + 1, b[id]});
  39.         }
  40.     }
  41.     cout << q.size() << "\n";
  42.     for(int i = 1; i <= n; i++) {
  43.         cout << b[i] << "\n";
  44.     }
  45.     return 0;
  46. }

雷达设备

假设海岸是一条无限长的直线，陆地位于海岸的一侧，海洋位于另外一侧。
每个小岛都位于海洋一侧的某个点上。
雷达装置均位于海岸线上，且雷达的监测范围为 0x07 贪心 - 图58，当小岛与某雷达的距离不超过 0x07 贪心 - 图59 时，该小岛可以被雷达覆盖。
我们使用笛卡尔坐标系，定义海岸线为 0x07 贪心 - 图60 轴，海的一侧在 0x07 贪心 - 图61 轴上方，陆地一侧在 0x07 贪心 - 图62 轴下方。
现在给出每个小岛的具体坐标以及雷达的检测范围，请你求出能够使所有小岛都被雷达覆盖所需的最小雷达数目。
输入格式
第一行输入两个整数 0x07 贪心 - 图63 和 0x07 贪心 - 图64，分别代表小岛数目和雷达检测范围。
接下来 0x07 贪心 - 图65 行，每行输入两个整数，分别代表小岛的 0x07 贪心 - 图66 轴坐标。
同一行数据之间用空格隔开。
输出格式
输出一个整数，代表所需的最小雷达数目，若没有解决方案则所需数目输出 0x07 贪心 - 图67。
数据范围
0x07 贪心 - 图68,
0x07 贪心 - 图69
输入样例：

  1. 3 2
  2. 1 2
  3. -3 1
  4. 2 1

输出样例：

  1. 2

一个小岛要想被一个雷达覆盖，根据勾股定理，可以计算雷达的可行区间 [l, r] ，然后问题转换为若干个区间，问最少有多少个点可以将所有区间覆盖。
对区间按照左端点排序，然后从左到右依次考虑。尽可能的将雷达往右放置。

  1. #include <bits/stdc++.h>
  2. using namespace std;
  3. struct node{
  4.     double l,r;
  5. }a[1010];
  6. int n;
  7. double d;
  8. bool cmp(node a,node b){
  9.     if(a.l==b.l)return a.r<b.r;
  10.     return a.l<b.l;
  11. }
  12. int main(){
  13.     scanf("%d%lf",&n,&d);
  14.     bool flag = false;
  15.     for(int i=0;i<n;i++){
  16.         double x,y;
  17.         scanf("%lf%lf",&x,&y);
  18.         if(y>d)flag = true;
  19.         a[i].l = x-sqrt(d*d-y*y);
  20.         a[i].r = 2*x-a[i].l;
  21.     }
  22.     if(flag){
  23.         cout<<-1<<endl;
  24.         return 0;
  25.     }
  26.     sort(a,a+n,cmp);
  27.     int num = 1;
  28.     double left = a[0].r;
  29.     for(int i=1;i<n;i++)
  30.         if(left>=a[i].l)
  31.             left = min(left,a[i].r);
  32.         else{
  33.             left = a[i].r;
  34.             num++;
  35.         }
  36.     cout<<num<<endl;
  37.     return 0;
  38. }

国王游戏

恰逢 0x07 贪心 - 图70 国国庆，国王邀请 0x07 贪心 - 图71 位大臣来玩一个有奖游戏。
首先，他让每个大臣在左、右手上面分别写下一个整数，国王自己也在左、右手上各写一个整数。
然后，让这 0x07 贪心 - 图72 位大臣排成一排，国王站在队伍的最前面。
排好队后，所有的大臣都会获得国王奖赏的若干金币，每位大臣获得的金币数分别是:
排在该大臣前面的所有人的左手上的数的乘积除以他自己右手上的数，然后向下取整得到的结果。
国王不希望某一个大臣获得特别多的奖赏，所以他想请你帮他重新安排一下队伍的顺序，使得获得奖赏最多的大臣，所获奖赏尽可能的少。
注意，国王的位置始终在队伍的最前面。
输入格式
第一行包含一个整数 0x07 贪心 - 图73，表示大臣的人数。
第二行包含两个整数 0x07 贪心 - 图74 和 0x07 贪心 - 图75，之间用一个空格隔开，分别表示国王左手和右手上的整数。
接下来 0x07 贪心 - 图76 行，每行包含两个整数 0x07 贪心 - 图77 和 0x07 贪心 - 图78，之间用一个空格隔开，分别表示每个大臣左手和右手上的整数。
输出格式
输出只有一行，包含一个整数，表示重新排列后的队伍中获奖赏最多的大臣所获得的金币数。
数据范围
0x07 贪心 - 图79
0x07 贪心 - 图80
输入样例：

  1. 3
  2. 1 1
  3. 2 3
  4. 7 4
  5. 4 6

输出样例：

  1. 2

每个大臣获得的金币是前面所有人左手数量的乘积除以自己右手的乘积。
设前 i - 1 个人左手乘积为 mul，我们来考虑第 i 个人与第 i + 1 个人的获得金币的情况。
0x07 贪心 - 图81，如果第 i 个人与第 i + 1 个人交换，则变为0x07 贪心 - 图82。
所以，如果前者大于后者，那么这次交换将会使得答案变得更小：
0x07 贪心 - 图83%20%26gt%3B%20max(mul%20%2F%20r%7Bi%2B1%7D%2C%20mul%20*%20l%7Bi%2B1%7D%20%2F%20ri)%3C%2Ftitle%3E%0A%3Cdefs%20aria-hidden%3D%22true%22%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-6D%22%20d%3D%22M21%20287Q22%20293%2024%20303T36%20341T56%20388T88%20425T132%20442T175%20435T205%20417T221%20395T229%20376L231%20369Q231%20367%20232%20367L243%20378Q303%20442%20384%20442Q401%20442%20415%20440T441%20433T460%20423T475%20411T485%20398T493%20385T497%20373T500%20364T502%20357L510%20367Q573%20442%20659%20442Q713%20442%20746%20415T780%20336Q780%20285%20742%20178T704%2050Q705%2036%20709%2031T724%2026Q752%2026%20776%2056T815%20138Q818%20149%20821%20151T837%20153Q857%20153%20857%20145Q857%20144%20853%20130Q845%20101%20831%2073T785%2017T716%20-10Q669%20-10%20648%2017T627%2073Q627%2092%20663%20193T700%20345Q700%20404%20656%20404H651Q565%20404%20506%20303L499%20291L466%20157Q433%2026%20428%2016Q415%20-11%20385%20-11Q372%20-11%20364%20-4T353%208T350%2018Q350%2029%20384%20161L420%20307Q423%20322%20423%20345Q423%20404%20379%20404H374Q288%20404%20229%20303L222%20291L189%20157Q156%2026%20151%2016Q138%20-11%20108%20-11Q95%20-11%2087%20-5T76%207T74%2017Q74%2030%20112%20181Q151%20335%20151%20342Q154%20357%20154%20369Q154%20405%20129%20405Q107%20405%2092%20377T69%20316T57%20280Q55%20278%2041%20278H27Q21%20284%2021%20287Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-61%22%20d%3D%22M33%20157Q33%20258%20109%20349T280%20441Q331%20441%20370%20392Q386%20422%20416%20422Q429%20422%20439%20414T449%20394Q449%20381%20412%20234T374%2068Q374%2043%20381%2035T402%2026Q411%2027%20422%2035Q443%2055%20463%20131Q469%20151%20473%20152Q475%20153%20483%20153H487Q506%20153%20506%20144Q506%20138%20501%20117T481%2063T449%2013Q436%200%20417%20-8Q409%20-10%20393%20-10Q359%20-10%20336%205T306%2036L300%2051Q299%2052%20296%2050Q294%2048%20292%2046Q233%20-10%20172%20-10Q117%20-10%2075%2030T33%20157ZM351%20328Q351%20334%20346%20350T323%20385T277%20405Q242%20405%20210%20374T160%20293Q131%20214%20119%20129Q119%20126%20119%20118T118%20106Q118%2061%20136%2044T179%2026Q217%2026%20254%2059T298%20110Q300%20114%20325%20217T351%20328Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-78%22%20d%3D%22M52%20289Q59%20331%20106%20386T222%20442Q257%20442%20286%20424T329%20379Q371%20442%20430%20442Q467%20442%20494%20420T522%20361Q522%20332%20508%20314T481%20292T458%20288Q439%20288%20427%20299T415%20328Q415%20374%20465%20391Q454%20404%20425%20404Q412%20404%20406%20402Q368%20386%20350%20336Q290%20115%20290%2078Q290%2050%20306%2038T341%2026Q378%2026%20414%2059T463%20140Q466%20150%20469%20151T485%20153H489Q504%20153%20504%20145Q504%20144%20502%20134Q486%2077%20440%2033T333%20-11Q263%20-11%20227%2052Q186%20-10%20133%20-10H127Q78%20-10%2057%2016T35%2071Q35%20103%2054%20123T99%20143Q142%20143%20142%20101Q142%2081%20130%2066T107%2046T94%2041L91%2040Q91%2039%2097%2036T113%2029T132%2026Q168%2026%20194%2071Q203%2087%20217%20139T245%20247T261%20313Q266%20340%20266%20352Q266%20380%20251%20392T217%20404Q177%20404%20142%20372T93%20290Q91%20281%2088%20280T72%20278H58Q52%20284%2052%20289Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-28%22%20d%3D%22M94%20250Q94%20319%20104%20381T127%20488T164%20576T202%20643T244%20695T277%20729T302%20750H315H319Q333%20750%20333%20741Q333%20738%20316%20720T275%20667T226%20581T184%20443T167%20250T184%2058T225%20-81T274%20-167T316%20-220T333%20-241Q333%20-250%20318%20-250H315H302L274%20-226Q180%20-141%20137%20-14T94%20250Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-75%22%20d%3D%22M21%20287Q21%20295%2030%20318T55%20370T99%20420T158%20442Q204%20442%20227%20417T250%20358Q250%20340%20216%20246T182%20105Q182%2062%20196%2045T238%2027T291%2044T328%2078L339%2095Q341%2099%20377%20247Q407%20367%20413%20387T427%20416Q444%20431%20463%20431Q480%20431%20488%20421T496%20402L420%2084Q419%2079%20419%2068Q419%2043%20426%2035T447%2026Q469%2029%20482%2057T512%20145Q514%20153%20532%20153Q551%20153%20551%20144Q550%20139%20549%20130T540%2098T523%2055T498%2017T462%20-8Q454%20-10%20438%20-10Q372%20-10%20347%2046Q345%2045%20336%2036T318%2021T296%206T267%20-6T233%20-11Q189%20-11%20155%207Q103%2038%20103%20113Q103%20170%20138%20262T173%20379Q173%20380%20173%20381Q173%20390%20173%20393T169%20400T158%20404H154Q131%20404%20112%20385T82%20344T65%20302T57%20280Q55%20278%2041%20278H27Q21%20284%2021%20287Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-6C%22%20d%3D%22M117%2059Q117%2026%20142%2026Q179%2026%20205%20131Q211%20151%20215%20152Q217%20153%20225%20153H229Q238%20153%20241%20153T246%20151T248%20144Q247%20138%20245%20128T234%2090T214%2043T183%206T137%20-11Q101%20-11%2070%2011T38%2085Q38%2097%2039%20102L104%20360Q167%20615%20167%20623Q167%20626%20166%20628T162%20632T157%20634T149%20635T141%20636T132%20637T122%20637Q112%20637%20109%20637T101%20638T95%20641T94%20647Q94%20649%2096%20661Q101%20680%20107%20682T179%20688Q194%20689%20213%20690T243%20693T254%20694Q266%20694%20266%20686Q266%20675%20193%20386T118%2083Q118%2081%20118%2075T117%2065V59Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-2F%22%20d%3D%22M423%20750Q432%20750%20438%20744T444%20730Q444%20725%20271%20248T92%20-240Q85%20-250%2075%20-250Q68%20-250%2062%20-245T56%20-231Q56%20-221%20230%20257T407%20740Q411%20750%20423%20750Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-72%22%20d%3D%22M21%20287Q22%20290%2023%20295T28%20317T38%20348T53%20381T73%20411T99%20433T132%20442Q161%20442%20183%20430T214%20408T225%20388Q227%20382%20228%20382T236%20389Q284%20441%20347%20441H350Q398%20441%20422%20400Q430%20381%20430%20363Q430%20333%20417%20315T391%20292T366%20288Q346%20288%20334%20299T322%20328Q322%20376%20378%20392Q356%20405%20342%20405Q286%20405%20239%20331Q229%20315%20224%20298T190%20165Q156%2025%20151%2016Q138%20-11%20108%20-11Q95%20-11%2087%20-5T76%207T74%2017Q74%2030%20114%20189T154%20366Q154%20405%20128%20405Q107%20405%2092%20377T68%20316T57%20280Q55%20278%2041%20278H27Q21%20284%2021%20287Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-69%22%20d%3D%22M184%20600Q184%20624%20203%20642T247%20661Q265%20661%20277%20649T290%20619Q290%20596%20270%20577T226%20557Q211%20557%20198%20567T184%20600ZM21%20287Q21%20295%2030%20318T54%20369T98%20420T158%20442Q197%20442%20223%20419T250%20357Q250%20340%20236%20301T196%20196T154%2083Q149%2061%20149%2051Q149%2026%20166%2026Q175%2026%20185%2029T208%2043T235%2078T260%20137Q263%20149%20265%20151T282%20153Q302%20153%20302%20143Q302%20135%20293%20112T268%2061T223%2011T161%20-11Q129%20-11%20102%2010T74%2074Q74%2091%2079%20106T122%20220Q160%20321%20166%20341T173%20380Q173%20404%20156%20404H154Q124%20404%2099%20371T61%20287Q60%20286%2059%20284T58%20281T56%20279T53%20278T49%20278T41%20278H27Q21%20284%2021%20287Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-2C%22%20d%3D%22M78%2035T78%2060T94%20103T137%20121Q165%20121%20187%2096T210%208Q210%20-27%20201%20-60T180%20-117T154%20-158T130%20-185T117%20-194Q113%20-194%20104%20-185T95%20-172Q95%20-168%20106%20-156T131%20-126T157%20-76T173%20-3V9L172%208Q170%207%20167%206T161%203T152%201T140%200Q113%200%2096%2017Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-2217%22%20d%3D%22M229%20286Q216%20420%20216%20436Q216%20454%20240%20464Q241%20464%20245%20464T251%20465Q263%20464%20273%20456T283%20436Q283%20419%20277%20356T270%20286L328%20328Q384%20369%20389%20372T399%20375Q412%20375%20423%20365T435%20338Q435%20325%20425%20315Q420%20312%20357%20282T289%20250L355%20219L425%20184Q434%20175%20434%20161Q434%20146%20425%20136T401%20125Q393%20125%20383%20131T328%20171L270%20213Q283%2079%20283%2063Q283%2053%20276%2044T250%2035Q231%2035%20224%2044T216%2063Q216%2080%20222%20143T229%20213L171%20171Q115%20130%20110%20127Q106%20124%20100%20124Q87%20124%2076%20134T64%20161Q64%20166%2064%20169T67%20175T72%20181T81%20188T94%20195T113%20204T138%20215T170%20230T210%20250L74%20315Q65%20324%2065%20338Q65%20353%2074%20363T98%20374Q106%20374%20116%20368T171%20328L229%20286Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-2B%22%20d%3D%22M56%20237T56%20250T70%20270H369V420L370%20570Q380%20583%20389%20583Q402%20583%20409%20568V270H707Q722%20262%20722%20250T707%20230H409V-68Q401%20-82%20391%20-82H389H387Q375%20-82%20369%20-68V230H70Q56%20237%2056%20250Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-31%22%20d%3D%22M213%20578L200%20573Q186%20568%20160%20563T102%20556H83V602H102Q149%20604%20189%20617T245%20641T273%20663Q275%20666%20285%20666Q294%20666%20302%20660V361L303%2061Q310%2054%20315%2052T339%2048T401%2046H427V0H416Q395%203%20257%203Q121%203%20100%200H88V46H114Q136%2046%20152%2046T177%2047T193%2050T201%2052T207%2057T213%2061V578Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-29%22%20d%3D%22M60%20749L64%20750Q69%20750%2074%20750H86L114%20726Q208%20641%20251%20514T294%20250Q294%20182%20284%20119T261%2012T224%20-76T186%20-143T145%20-194T113%20-227T90%20-246Q87%20-249%2086%20-250H74Q66%20-250%2063%20-250T58%20-247T55%20-238Q56%20-237%2066%20-225Q221%20-64%20221%20250T66%20725Q56%20737%2055%20738Q55%20746%2060%20749Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-3E%22%20d%3D%22M84%20520Q84%20528%2088%20533T96%20539L99%20540Q106%20540%20253%20471T544%20334L687%20265Q694%20260%20694%20250T687%20235Q685%20233%20395%2096L107%20-40H101Q83%20-38%2083%20-20Q83%20-19%2083%20-17Q82%20-10%2098%20-1Q117%209%20248%2071Q326%20108%20378%20132L626%20250L378%20368Q90%20504%2086%20509Q84%20513%2084%20520Z%22%3E%3C%2Fpath%3E%0A%3C%2Fdefs%3E%0A%3Cg%20stroke%3D%22currentColor%22%20fill%3D%22currentColor%22%20stroke-width%3D%220%22%20transform%3D%22matrix(1%200%200%20-1%200%200)%22%20aria-hidden%3D%22true%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-6D%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-61%22%20x%3D%22878%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-78%22%20x%3D%221408%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-28%22%20x%3D%221980%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-6D%22%20x%3D%222370%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-75%22%20x%3D%223248%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-6C%22%20x%3D%223821%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2F%22%20x%3D%224119%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(4620%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-72%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-69%22%20x%3D%22638%22%20y%3D%22-213%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2C%22%20x%3D%225415%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-6D%22%20x%3D%225860%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-75%22%20x%3D%226739%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-6C%22%20x%3D%227311%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2217%22%20x%3D%227832%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(8555%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-6C%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-69%22%20x%3D%22422%22%20y%3D%22-213%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2F%22%20x%3D%229198%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(9698%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-72%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(451%2C-150)%22%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-69%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-2B%22%20x%3D%22345%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-31%22%20x%3D%221124%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-29%22%20x%3D%2211398%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-3E%22%20x%3D%2212066%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-6D%22%20x%3D%2213122%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-61%22%20x%3D%2214000%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-78%22%20x%3D%2214530%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-28%22%20x%3D%2215102%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-6D%22%20x%3D%2215492%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-75%22%20x%3D%2216370%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-6C%22%20x%3D%2216943%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2F%22%20x%3D%2217241%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(17742%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-72%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(451%2C-150)%22%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-69%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-2B%22%20x%3D%22345%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-31%22%20x%3D%221124%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2C%22%20x%3D%2219442%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-6D%22%20x%3D%2219887%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-75%22%20x%3D%2220766%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-6C%22%20x%3D%2221338%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2217%22%20x%3D%2221859%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(22582%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-6C%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(298%2C-150)%22%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-69%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-2B%22%20x%3D%22345%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-31%22%20x%3D%221124%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2F%22%20x%3D%2224129%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(24629%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-72%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-69%22%20x%3D%22638%22%20y%3D%22-213%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-29%22%20x%3D%2225425%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fsvg%3E#card=math&code=max%28mul%20%2F%20r_i%2C%20mul%20%2A%20l_i%20%2F%20r%7Bi%2B1%7D%29%20%3E%20max%28mul%20%2F%20r%7Bi%2B1%7D%2C%20mul%20%2A%20l%7Bi%2B1%7D%20%2F%20ri%29%0A&id=VK5Uw)
整体通分，即：
![](data:image/svg+xml;utf8,%3Csvg%20xmlns%3Axlink%3D%22http%3A%2F%2Fwww.w3.org%2F1999%2Fxlink%22%20width%3D%2239.055ex%22%20height%3D%222.843ex%22%20style%3D%22vertical-align%3A%20-0.838ex%3B%22%20viewBox%3D%220%20-863.1%2016815.3%201223.9%22%20role%3D%22img%22%20focusable%3D%22false%22%20xmlns%3D%22http%3A%2F%2Fwww.w3.org%2F2000%2Fsvg%22%20aria-labelledby%3D%22MathJax-SVG-1-Title%22%3E%0A%3Ctitle%20id%3D%22MathJax-SVG-1-Title%22%3Emax(r%7Bi%2B1%7D%2C%20li*r_i)%20%26gt%3B%20max(r%7Bi%7D%2C%20l%7Bi%2B1%7D*r%7Bi%2B1%7D)%3C%2Ftitle%3E%0A%3Cdefs%20aria-hidden%3D%22true%22%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-6D%22%20d%3D%22M21%20287Q22%20293%2024%20303T36%20341T56%20388T88%20425T132%20442T175%20435T205%20417T221%20395T229%20376L231%20369Q231%20367%20232%20367L243%20378Q303%20442%20384%20442Q401%20442%20415%20440T441%20433T460%20423T475%20411T485%20398T493%20385T497%20373T500%20364T502%20357L510%20367Q573%20442%20659%20442Q713%20442%20746%20415T780%20336Q780%20285%20742%20178T704%2050Q705%2036%20709%2031T724%2026Q752%2026%20776%2056T815%20138Q818%20149%20821%20151T837%20153Q857%20153%20857%20145Q857%20144%20853%20130Q845%20101%20831%2073T785%2017T716%20-10Q669%20-10%20648%2017T627%2073Q627%2092%20663%20193T700%20345Q700%20404%20656%20404H651Q565%20404%20506%20303L499%20291L466%20157Q433%2026%20428%2016Q415%20-11%20385%20-11Q372%20-11%20364%20-4T353%208T350%2018Q350%2029%20384%20161L420%20307Q423%20322%20423%20345Q423%20404%20379%20404H374Q288%20404%20229%20303L222%20291L189%20157Q156%2026%20151%2016Q138%20-11%20108%20-11Q95%20-11%2087%20-5T76%207T74%2017Q74%2030%20112%20181Q151%20335%20151%20342Q154%20357%20154%20369Q154%20405%20129%20405Q107%20405%2092%20377T69%20316T57%20280Q55%20278%2041%20278H27Q21%20284%2021%20287Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-61%22%20d%3D%22M33%20157Q33%20258%20109%20349T280%20441Q331%20441%20370%20392Q386%20422%20416%20422Q429%20422%20439%20414T449%20394Q449%20381%20412%20234T374%2068Q374%2043%20381%2035T402%2026Q411%2027%20422%2035Q443%2055%20463%20131Q469%20151%20473%20152Q475%20153%20483%20153H487Q506%20153%20506%20144Q506%20138%20501%20117T481%2063T449%2013Q436%200%20417%20-8Q409%20-10%20393%20-10Q359%20-10%20336%205T306%2036L300%2051Q299%2052%20296%2050Q294%2048%20292%2046Q233%20-10%20172%20-10Q117%20-10%2075%2030T33%20157ZM351%20328Q351%20334%20346%20350T323%20385T277%20405Q242%20405%20210%20374T160%20293Q131%20214%20119%20129Q119%20126%20119%20118T118%20106Q118%2061%20136%2044T179%2026Q217%2026%20254%2059T298%20110Q300%20114%20325%20217T351%20328Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-78%22%20d%3D%22M52%20289Q59%20331%20106%20386T222%20442Q257%20442%20286%20424T329%20379Q371%20442%20430%20442Q467%20442%20494%20420T522%20361Q522%20332%20508%20314T481%20292T458%20288Q439%20288%20427%20299T415%20328Q415%20374%20465%20391Q454%20404%20425%20404Q412%20404%20406%20402Q368%20386%20350%20336Q290%20115%20290%2078Q290%2050%20306%2038T341%2026Q378%2026%20414%2059T463%20140Q466%20150%20469%20151T485%20153H489Q504%20153%20504%20145Q504%20144%20502%20134Q486%2077%20440%2033T333%20-11Q263%20-11%20227%2052Q186%20-10%20133%20-10H127Q78%20-10%2057%2016T35%2071Q35%20103%2054%20123T99%20143Q142%20143%20142%20101Q142%2081%20130%2066T107%2046T94%2041L91%2040Q91%2039%2097%2036T113%2029T132%2026Q168%2026%20194%2071Q203%2087%20217%20139T245%20247T261%20313Q266%20340%20266%20352Q266%20380%20251%20392T217%20404Q177%20404%20142%20372T93%20290Q91%20281%2088%20280T72%20278H58Q52%20284%2052%20289Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-28%22%20d%3D%22M94%20250Q94%20319%20104%20381T127%20488T164%20576T202%20643T244%20695T277%20729T302%20750H315H319Q333%20750%20333%20741Q333%20738%20316%20720T275%20667T226%20581T184%20443T167%20250T184%2058T225%20-81T274%20-167T316%20-220T333%20-241Q333%20-250%20318%20-250H315H302L274%20-226Q180%20-141%20137%20-14T94%20250Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-72%22%20d%3D%22M21%20287Q22%20290%2023%20295T28%20317T38%20348T53%20381T73%20411T99%20433T132%20442Q161%20442%20183%20430T214%20408T225%20388Q227%20382%20228%20382T236%20389Q284%20441%20347%20441H350Q398%20441%20422%20400Q430%20381%20430%20363Q430%20333%20417%20315T391%20292T366%20288Q346%20288%20334%20299T322%20328Q322%20376%20378%20392Q356%20405%20342%20405Q286%20405%20239%20331Q229%20315%20224%20298T190%20165Q156%2025%20151%2016Q138%20-11%20108%20-11Q95%20-11%2087%20-5T76%207T74%2017Q74%2030%20114%20189T154%20366Q154%20405%20128%20405Q107%20405%2092%20377T68%20316T57%20280Q55%20278%2041%20278H27Q21%20284%2021%20287Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-69%22%20d%3D%22M184%20600Q184%20624%20203%20642T247%20661Q265%20661%20277%20649T290%20619Q290%20596%20270%20577T226%20557Q211%20557%20198%20567T184%20600ZM21%20287Q21%20295%2030%20318T54%20369T98%20420T158%20442Q197%20442%20223%20419T250%20357Q250%20340%20236%20301T196%20196T154%2083Q149%2061%20149%2051Q149%2026%20166%2026Q175%2026%20185%2029T208%2043T235%2078T260%20137Q263%20149%20265%20151T282%20153Q302%20153%20302%20143Q302%20135%20293%20112T268%2061T223%2011T161%20-11Q129%20-11%20102%2010T74%2074Q74%2091%2079%20106T122%20220Q160%20321%20166%20341T173%20380Q173%20404%20156%20404H154Q124%20404%2099%20371T61%20287Q60%20286%2059%20284T58%20281T56%20279T53%20278T49%20278T41%20278H27Q21%20284%2021%20287Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-2B%22%20d%3D%22M56%20237T56%20250T70%20270H369V420L370%20570Q380%20583%20389%20583Q402%20583%20409%20568V270H707Q722%20262%20722%20250T707%20230H409V-68Q401%20-82%20391%20-82H389H387Q375%20-82%20369%20-68V230H70Q56%20237%2056%20250Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-31%22%20d%3D%22M213%20578L200%20573Q186%20568%20160%20563T102%20556H83V602H102Q149%20604%20189%20617T245%20641T273%20663Q275%20666%20285%20666Q294%20666%20302%20660V361L303%2061Q310%2054%20315%2052T339%2048T401%2046H427V0H416Q395%203%20257%203Q121%203%20100%200H88V46H114Q136%2046%20152%2046T177%2047T193%2050T201%2052T207%2057T213%2061V578Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-2C%22%20d%3D%22M78%2035T78%2060T94%20103T137%20121Q165%20121%20187%2096T210%208Q210%20-27%20201%20-60T180%20-117T154%20-158T130%20-185T117%20-194Q113%20-194%20104%20-185T95%20-172Q95%20-168%20106%20-156T131%20-126T157%20-76T173%20-3V9L172%208Q170%207%20167%206T161%203T152%201T140%200Q113%200%2096%2017Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-6C%22%20d%3D%22M117%2059Q117%2026%20142%2026Q179%2026%20205%20131Q211%20151%20215%20152Q217%20153%20225%20153H229Q238%20153%20241%20153T246%20151T248%20144Q247%20138%20245%20128T234%2090T214%2043T183%206T137%20-11Q101%20-11%2070%2011T38%2085Q38%2097%2039%20102L104%20360Q167%20615%20167%20623Q167%20626%20166%20628T162%20632T157%20634T149%20635T141%20636T132%20637T122%20637Q112%20637%20109%20637T101%20638T95%20641T94%20647Q94%20649%2096%20661Q101%20680%20107%20682T179%20688Q194%20689%20213%20690T243%20693T254%20694Q266%20694%20266%20686Q266%20675%20193%20386T118%2083Q118%2081%20118%2075T117%2065V59Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-2217%22%20d%3D%22M229%20286Q216%20420%20216%20436Q216%20454%20240%20464Q241%20464%20245%20464T251%20465Q263%20464%20273%20456T283%20436Q283%20419%20277%20356T270%20286L328%20328Q384%20369%20389%20372T399%20375Q412%20375%20423%20365T435%20338Q435%20325%20425%20315Q420%20312%20357%20282T289%20250L355%20219L425%20184Q434%20175%20434%20161Q434%20146%20425%20136T401%20125Q393%20125%20383%20131T328%20171L270%20213Q283%2079%20283%2063Q283%2053%20276%2044T250%2035Q231%2035%20224%2044T216%2063Q216%2080%20222%20143T229%20213L171%20171Q115%20130%20110%20127Q106%20124%20100%20124Q87%20124%2076%20134T64%20161Q64%20166%2064%20169T67%20175T72%20181T81%20188T94%20195T113%20204T138%20215T170%20230T210%20250L74%20315Q65%20324%2065%20338Q65%20353%2074%20363T98%20374Q106%20374%20116%20368T171%20328L229%20286Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-29%22%20d%3D%22M60%20749L64%20750Q69%20750%2074%20750H86L114%20726Q208%20641%20251%20514T294%20250Q294%20182%20284%20119T261%2012T224%20-76T186%20-143T145%20-194T113%20-227T90%20-246Q87%20-249%2086%20-250H74Q66%20-250%2063%20-250T58%20-247T55%20-238Q56%20-237%2066%20-225Q221%20-64%20221%20250T66%20725Q56%20737%2055%20738Q55%20746%2060%20749Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-3E%22%20d%3D%22M84%20520Q84%20528%2088%20533T96%20539L99%20540Q106%20540%20253%20471T544%20334L687%20265Q694%20260%20694%20250T687%20235Q685%20233%20395%2096L107%20-40H101Q83%20-38%2083%20-20Q83%20-19%2083%20-17Q82%20-10%2098%20-1Q117%209%20248%2071Q326%20108%20378%20132L626%20250L378%20368Q90%20504%2086%20509Q84%20513%2084%20520Z%22%3E%3C%2Fpath%3E%0A%3C%2Fdefs%3E%0A%3Cg%20stroke%3D%22currentColor%22%20fill%3D%22currentColor%22%20stroke-width%3D%220%22%20transform%3D%22matrix(1%200%200%20-1%200%200)%22%20aria-hidden%3D%22true%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-6D%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-61%22%20x%3D%22878%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-78%22%20x%3D%221408%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-28%22%20x%3D%221980%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(2370%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-72%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(451%2C-150)%22%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-69%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-2B%22%20x%3D%22345%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-31%22%20x%3D%221124%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2C%22%20x%3D%224070%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(4515%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-6C%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-69%22%20x%3D%22422%22%20y%3D%22-213%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2217%22%20x%3D%225380%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(6103%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-72%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-69%22%20x%3D%22638%22%20y%3D%22-213%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-29%22%20x%3D%226898%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-3E%22%20x%3D%227566%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-6D%22%20x%3D%228622%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-61%22%20x%3D%229500%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-78%22%20x%3D%2210030%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-28%22%20x%3D%2210602%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(10992%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-72%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-69%22%20x%3D%22638%22%20y%3D%22-213%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2C%22%20x%3D%2211788%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(12233%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-6C%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(298%2C-150)%22%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-69%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-2B%22%20x%3D%22345%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-31%22%20x%3D%221124%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2217%22%20x%3D%2214002%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(14725%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-72%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(451%2C-150)%22%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMATHI-69%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-2B%22%20x%3D%22345%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-31%22%20x%3D%221124%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-29%22%20x%3D%2216425%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fsvg%3E#card=math&code=max%28r%7Bi%2B1%7D%2C%20l_i%2Ar_i%29%20%3E%20max%28r%7Bi%7D%2C%20l%7Bi%2B1%7D%2Ar%7Bi%2B1%7D%29%0A&id=sVtTN)
可以进一步化简：
0x07 贪心 - 图84
当上述条件发生时，应当置换顺序，所以，要按照 l * r 升序排列。
另外这个题目计算结果没有取模，所以需要用高精度乘法和除法。

  1. #include<bits/stdc++.h>
  2. using namespace std;
  3. #define rep(i,j,k) for(int i=int(j);i<=int(k);i++)
  4. #define per(i,j,k) for(int i=int(j);i>=int(k);i--)
  5. typedef long long ll;
  6. const int N = 100010;
  7. int n;
  8. pair<int,int> a[N];
  10. class Int {
  11. public:
  12.     Int(long long num = 0) { *this = num; }
  13.     Int(string str) { *this = str; }
  14.     Int(const Int& o) { this->s = o.s; }
  15.     Int(const vector<int> & o) { this->s = o; }
  17.     Int operator = (long long num) { transform(s, abs(num)); return *this; }
  18.     Int operator = (string &str) {
  19.         s.clear();
  20.         int x = 0, len = (str.length() + WIDTH - 1) / WIDTH;
  21.         for(int i = 0; i < len; i++){
  22.             int ed = str.length() - i * WIDTH;
  23.             int st = max(0, ed - WIDTH);
  24.             sscanf(str.substr(st, ed - st).c_str(), "%d", &x);
  25.             s.push_back(x);
  26.         }
  27.         adjust(s);
  28.         return *this;
  29.     }
  31.     bool operator < (Int &o) { return compare(s, o.s); }
  32.     bool operator > (Int &o) { return o < *this; }
  33.     bool operator <= (Int &o) { return !(o < *this); }
  34.     bool operator >= (Int &o) { return !(*this < o); }
  35.     bool operator == (Int &o) { return !(o < *this) && (*this < o); }
  37.     Int operator + (Int &o) { return Int(add(s, o.s)); };
  38.     Int operator - (Int &o) { return Int(sub(s, o.s)); };
  39.     Int operator * (Int &o) { return Int(mul(s, o.s)); };
  40.     Int operator * (int &o) { return Int(mul(s, o)); };
  41.     Int operator / (Int &o) { return *this < o ? 0 : Int(div(s, o.s)); };
  42.     Int operator / (int &o) { return Int(div(s, o)); };
  43.     friend ostream& operator << (ostream &out, const Int& x) {
  44.         out << x.s.back();
  45.         for(int i = x.s.size() - 2; i >= 0;i--){
  46.             char buf[20];
  47.             sprintf(buf,"%04d",x.s[i]);//08d此处的8应该与WIDTH一致
  48.             for(int j=0;j<strlen(buf);j++)out<<buf[j];
  49.         }
  50.         return out;
  51.     }
  52.     friend istream& operator >> (istream & in, Int & x){
  53.         string s;
  54.         if(!(in>>s))return in;
  55.         x = s;
  56.         return in;
  57.     }
  58. private:
  59.     bool compare(const vector<int> &A, const vector<int> &B) {
  60.         if(A.size() != B.size()) return A.size() < B.size();
  61.         for(int i = A.size() - 1; i >= 0; i--){
  62.             if(A[i] != B[i]) return A[i] < B[i];
  63.         }
  64.         return false; // 相等
  65.     }
  66.     vector<int> add(const vector<int> &A, const vector<int> &B) {
  67.         if(A.size() < B.size()) return add(B, A);
  68.         vector<int> C;
  69.         int t = 0;
  70.         for(int i = 0; i < A.size(); i++){
  71.             if(i < B.size()) t += B[i];
  72.             t += A[i];
  73.             C.push_back(t % BASE);
  74.             t /= BASE;
  75.         }
  76.         if(t) C.push_back(t);
  77.         adjust(C);
  78.         return C;
  79.     }
  80.     vector<int> sub(const vector<int> &A, const vector<int> &B) {
  81.         vector<int> C;
  82.         for(int i = 0, t = 0; i < A.size(); i++){
  83.             t = A[i] - t;
  84.             if(i < B.size()) t -= B[i];
  85.             C.push_back((t + BASE) % BASE);
  86.             t = t < 0 ? 1 : 0;
  87.         }
  88.         adjust(C); 
  89.         return C;
  90.     }
  91.     vector<int> mul(const vector<int> &A, const int& B) {
  92.         vector<int> C;
  93.         int t = 0;
  94.         for(int i = 0; i < A.size() || t; i ++) {
  95.             if(i < A.size()) t += A[i] * B;
  96.             C.push_back(t % BASE);
  97.             t /= BASE;
  98.         }
  99.         adjust(C);
  100.         return C;
  101.     }
  102.     vector<int> mul(const vector<int> &A, const vector<int> &B) {
  103.         int a = A.size(), b = B.size();
  104.         vector<int> C(a + b + 10, 0);
  105.         for(int i = 0; i < a; i ++) {
  106.             for(int j = 0; j < b; j++){
  107.                 C[i + j] += A[i] * B[j];
  108.             }
  109.         }
  110.         for(int i = 0; i < C.size(); i++){
  111.             if(C[i] >= BASE) {
  112.                 C[i + 1] += C[i] / BASE;
  113.                 C[i] %= BASE;
  114.             }
  115.         }
  116.         adjust(C);
  117.         return C;
  118.     }
  119.     vector<int> div(const vector<int> &A, const int &B) {
  120.         vector<int> C;
  121.         int r = 0;
  122.         for(int i = A.size() - 1; i >= 0; i--) {
  123.             r = r * BASE + A[i];
  124.             C.push_back(r / B);
  125.             r %= B;
  126.         }
  127.         reverse(C.begin(), C.end());
  128.         adjust(C);
  129.         transform(this->r, r);
  130.         return C;
  131.     }
  132.     vector<int> div(vector<int> A,  vector<int> B){
  133.         int a = A.size(), b = B.size();
  134.         int dv = a - b;
  135.         vector<int> C(dv + 1, 0);
  136.         reverse(B.begin(), B.end());
  137.         for(int i = 0; i < dv; i++) B.push_back(0);
  138.         reverse(B.begin(), B.end());
  139.         b = a;
  140.         for(int i = 0; i <= dv; i++){
  141.             while(!compare(A, B)) {
  142.                 A = sub(A, B);
  143.                 C[dv - i] ++;
  144.             }
  145.             B.erase(B.begin());
  146.         }
  147.         this->r = A;
  148.         adjust(C);
  149.         return C;
  150.     }
  152.     void transform(vector<int> &A, long long B){
  153.         A.clear();
  154.         do {
  155.             A.push_back(B % BASE);
  156.             B /= BASE;
  157.         } while(B > 0);
  158.     }
  159.     void adjust(vector<int> &A) {
  160.         while(A.size() > 1 && A.back() == 0) A.pop_back();
  161.     }
  164.     static const int BASE = 10000;
  165.     static const int WIDTH = 4;
  166.     vector<int> s;
  167.     vector<int> r;
  168. };
  170. int main(){
  171.   scanf("%d", &n);
  172.   rep(i,0,n) {
  173.     scanf("%d%d", &a[i].first, &a[i].second);
  174.   }
  175.   sort(a + 1, a + 1 + n, [](pair<int,int> a, pair<int,int> b) { return a.first * a.second < b.first * b.second; });
  176.   Int rs = 0, now = 0, pre = a[0].first;
  177.   rep(i,1,n) {
  178.     if(a[i].second != 0) now = pre / a[i].second;
  179.     if(a[i].first == 0) break;
  180.     pre = pre * a[i].first;
  181.     if(rs < now) rs = now;
  182.   }
  183.   cout << rs << endl;
  184.   return 0;
  185. }

给树染色

一颗树有 0x07 贪心 - 图85 个节点，这些节点被标号为：0x07 贪心 - 图86，每个节点 0x07 贪心 - 图87 都有一个权值 0x07 贪心 - 图88。
现在要把这棵树的节点全部染色，染色的规则是：
根节点 0x07 贪心 - 图89 可以随时被染色；对于其他节点，在被染色之前它的父亲节点必须已经染上了色。
每次染色的代价为 0x07 贪心 - 图90，其中 0x07 贪心 - 图91 代表当前是第几次染色。
求把这棵树染色的最小总代价。
输入格式
第一行包含两个整数 0x07 贪心 - 图92 和 0x07 贪心 - 图93，分别代表树的节点数以及根节点的序号。
第二行包含 0x07 贪心 - 图94 个整数，代表所有节点的权值，第 0x07 贪心 - 图95 个数即为第 0x07 贪心 - 图96 个节点的权值 0x07 贪心 - 图97。
接下来 0x07 贪心 - 图98 行，每行包含两个整数 0x07 贪心 - 图99 和 0x07 贪心 - 图100，代表两个节点的序号，两节点满足关系： 0x07 贪心 - 图101 节点是 0x07 贪心 - 图102 节点的父节点。
除根节点外的其他 0x07 贪心 - 图103 个节点的父节点和它们本身会在这 0x07 贪心 - 图104 行中表示出来。
同一行内的数用空格隔开。
输出格式
输出一个整数，代表把这棵树染色的最小总代价。
数据范围
0x07 贪心 - 图105,
0x07 贪心 - 图106
输入样例：

  1. 5 1
  2. 1 2 1 2 4
  3. 1 2
  4. 1 3
  5. 2 4
  6. 3 5

输出样例：

  1. 33

前置知识：并查集
一个贪心思路是每次从当前可以染色的集合中选择一个权值最大的点进行染色。但这样的策略是错误的，很容易构造一个极端的例子——让一个权值很小的节点下边有很多权值巨大的结点，另一个权值较大的节点却没有子节点。
有一个重要的性质：整个树中，除去根结点外权值最大的点一定会在其父节点染色后立即染色。
于是可以将其与父节点“合并起来”。合并得到的新点权值设置为这两个点的权值的平均值。
合并这个操作可以使用并查集，每个集合中包含了集合内部的染色顺序。
总体复杂度 0x07 贪心 - 图107

  1. #include<bits/stdc++.h>
  2. using namespace std;
  3. #define rep(i,j,k) for(int i=int(j);i<=int(k);i++)
  4. #define per(i,j,k) for(int i=int(j);i>=int(k);i--)
  5. typedef long long ll;
  6. const int N = 1010;
  7. int n, rt, val[N], f[N], fat[N];
  8. struct Node {
  9.     int v, s;
  10.     vector<int> ord;
  11. }a[N];
  12. int get(int x){ return x == f[x] ? x : f[x] = get(f[x]); }
  13. int main(){
  14.     scanf("%d%d", &n, &rt);
  15.     rep(i,1,n) {
  16.         scanf("%d", &a[i].v);
  17.         a[i].s = 1;
  18.         a[i].ord = {i};
  19.         val[i] = a[i].v;
  20.         f[i] = i;
  21.     }
  22.     rep(i,1,n-1) {
  23.         int x, y; scanf("%d%d", &x, &y);
  24.         fat[y] = x;
  25.     }
  26.     rep(i,1,n-1) {
  27.         int x = -1, v = -1, s = 1;
  28.         rep(j,1,n) {
  29.             if(j != rt && (x == -1 || (v * a[j].s < a[j].v * s))) {
  30.                 x = j, v = a[j].v, s = a[j].s;
  31.             }
  32.         }
  33.         int fa = get(fat[x]);
  34.         a[fa].v += a[x].v; a[fa].s += a[x].s;
  35.         a[fa].ord.insert(a[fa].ord.end(), a[x].ord.begin(), a[x].ord.end());
  36.         a[x].ord.clear();
  37.         a[x].v = -1; a[x].s = 1;
  38.         f[x] = fa;
  39.     }
  40.     int rs = 0;
  41.     for(int i = 0; i < a[rt].ord.size(); i++){
  42.         rs += (i + 1) * val[a[rt].ord[i]];
  43.     }
  44.     printf("%d\n", rs);
  45.     return 0;
  46. }

另外，结构体中的 ord 可以省去。采用前缀累计贡献的思考方式计算答案：
总体复杂度没有变，常数变小。

  1. #include<bits/stdc++.h>
  2. using namespace std;
  3. #define rep(i,j,k) for(int i=int(j);i<=int(k);i++)
  4. #define per(i,j,k) for(int i=int(j);i>=int(k);i--)
  5. typedef long long ll;
  6. const int N = 1010;
  7. int n, rt, rs, f[N], fat[N];
  8. struct Node {
  9.     int v, s;
  10. }a[N];
  11. int get(int x){ return x == f[x] ? x : f[x] = get(f[x]); }
  12. int main(){
  13.     scanf("%d%d", &n, &rt);
  14.     rep(i,1,n) {
  15.         scanf("%d", &a[i].v);
  16.         rs += a[i].v;
  17.         a[i].s = 1;
  18.         f[i] = i;
  19.     }
  20.     rep(i,1,n-1) {
  21.         int x, y; scanf("%d%d", &x, &y);
  22.         fat[y] = x;
  23.     }
  25.     rep(i,1,n-1) {
  26.         int x = -1, v = -1, s = 1;
  27.         rep(j,1,n) {
  28.             if(j != rt && (x == -1 || (v * a[j].s < a[j].v * s))) {
  29.                 x = j, v = a[j].v, s = a[j].s;
  30.             }
  31.         }
  32.         int fa = get(fat[x]);
  33.         rs += a[fa].s * a[x].v;
  34.         a[fa].v += a[x].v; a[fa].s += a[x].s;
  35.         a[x].v = -1; a[x].s = 1;
  36.         f[x] = fa;
  37.     }
  38.     printf("%d\n", rs);
  39.     return 0;
  40. }