包含 min 函数的栈

设计一个支持push，pop，top等操作并且可以在O(1)时间内检索出最小元素的堆栈。

• push(x)–将元素x插入栈中
• pop()–移除栈顶元素
• top()–得到栈顶元素
• getMin()–得到栈中最小元素

Sample

MinStack minStack = new MinStack();
minStack.push(-1);
minStack.push(3);
minStack.push(-4);
minStack.getMin();   --> Returns -4.
minStack.pop();
minStack.top();      --> Returns 3.
minStack.getMin();   --> Returns -1.

构造第二个栈，栈中第 i 个元素的值，是第一个栈中第 1∼i 个元素中的最小值。

class MinStack {
    public:
    int st[10010];
    int top1;
    int st2[10010];
    int top2;
    int cur;
    /** initialize your data structure here. */
    MinStack() {
        top1 = 0;
        top2 = 0;
        cur = 1e9;
        st2[0] = 1e9;
    }
    void push(int x) {
        cur = min(cur,x);
        st[++top1] = x;
        st2[++top2] = cur;
    }
    void pop() {
        cur = st2[--top2];
        top1--;
    }
    int top() {
        return st[top1];
    }
    int getMin() {
        if(top2==0)return 0;
        return st2[top2];
    }
};

编辑器

维护两个栈即可

#include<bits/stdc++.h>
using namespace std;
const int N=1000010;
int q;
int prest[N], sufst[N], t1, t2;
int sum[N], maxsum[N];
char op[2];
int x;
int main(){
    scanf("%d", &q);
    maxsum[0] = -1e9;
    while(q--){
        scanf("%s", op);
        switch (op[0])
        {
            case 'I': 
                scanf("%d", &x);
                prest[++t1] = x;
                sum[t1] = sum[t1-1] + x;
                maxsum[t1] = max(sum[t1], maxsum[t1-1]);
                break;
            case 'D':
                if(t1 != 0) t1--;
                break;
            case 'L':
                if(t1 != 0) {
                    sufst[++t2] = prest[t1--];
                }
                break;
            case 'R':
                if(t2 != 0) {
                    prest[++t1] = sufst[t2--];
                    sum[t1] = sum[t1-1] + prest[t1];
                    maxsum[t1] = max(sum[t1], maxsum[t1-1]);
                }
                break;
            case 'Q':
                scanf("%d", &x);
                printf("%d\n", maxsum[x]);
                break;
        }
    }
    return 0;
}

火车进栈

递归：

1. 如果当前栈中有元素，则优先出栈（因为这样会使得字典序更小）
2. 元素进栈

   #include <bits/stdc++.h>
   using namespace std;
   int n,cnt = 0;
   int st[50],tp;
   vector<int> res;
   void dfs(int tp,int x){
    if(cnt >= 20)return;
    if(x > n && tp == 0){
        cnt++;
        for(int i=0;i<res.size();i++)
            cout << res[i];
        puts("");
        return;
    }
    if(tp){ // 有元素，就尝试出栈
        int now = st[tp];
        res.push_back(now);
        dfs(tp-1,x);
        res.pop_back();
        st[tp] = now;
    }
    if(x <= n){
        st[tp+1] = x;
        dfs(tp+1,x+1);
    }
   }
   int main(){
    scanf("%d",&n);
    dfs(0,1);
    return 0;
   }

   火车进出栈问题

   Acwing 上题目数据范围较大，可在Luogu上找小范围数据的原题（可通过 ）
   求长度为 n 的序列的出栈序列种数。
   方法一：首先递归枚举可以用 的时间内解决该题。
   方法二：然后可以考虑使用「动态规划」的思想进行递推。
   设 s[n] 为长度为 n 的序列的出栈序列种数，考虑 1 这个数的出栈位置为 k，那么出栈序列可以分为前 k-1 个数和后 n-k 个数。这两部分是独立的，所以：。
   时间复杂度为 。
   方法三：另外一种DP状态可以定义为：f[i][j] 表示为有 i 个数还没有进栈，有 j 个数字还没有出栈的方案数。
   初始状态（可以直接指定答案的状态）：f[0][0]=1
   目标状态：f[n][0]
   转移方程：f[i][j] = f[i-1][j+1] + f[i][j-1]
   时间复杂度仍然为 。
   方法四：可以直接用 Catalan 数计算：。组合数学一节将介绍。

   直方图中最大的矩形

   
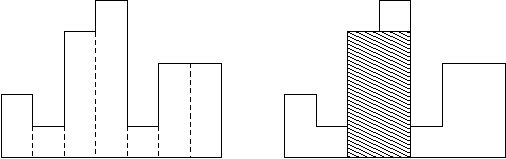
   先思考暴力做法：对于每个矩形，把它作为右边界，然后枚举左边的矩形作为左边界，枚举方向为从右至左。然后可以计算出每种情况下的最大面积。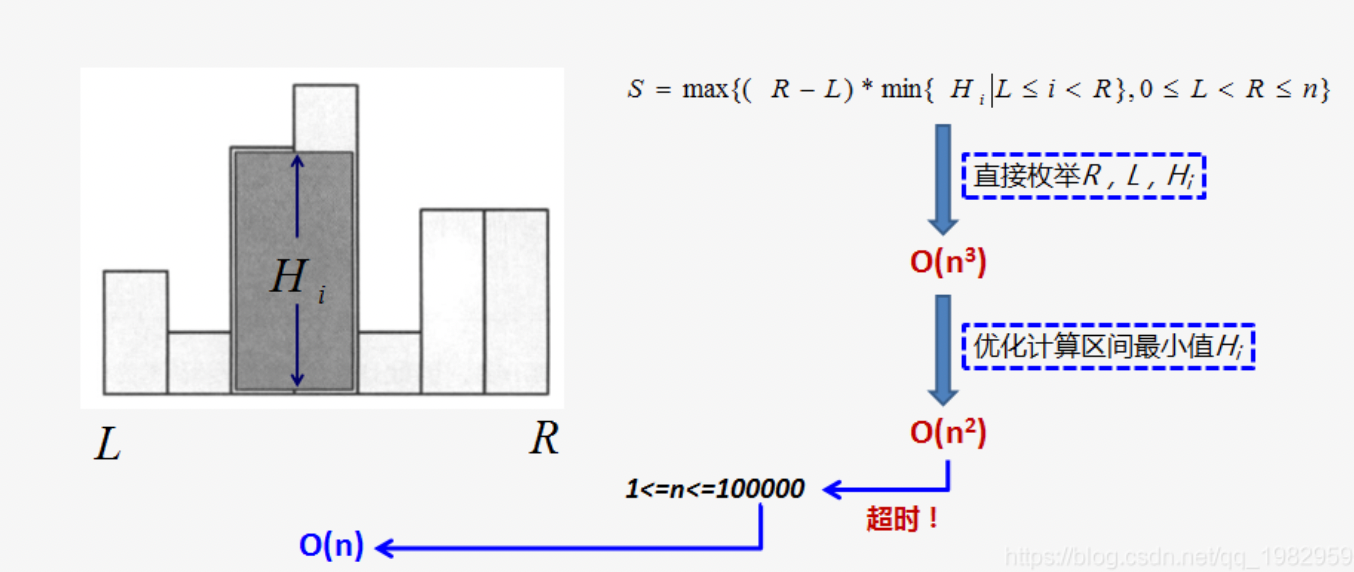
   
   
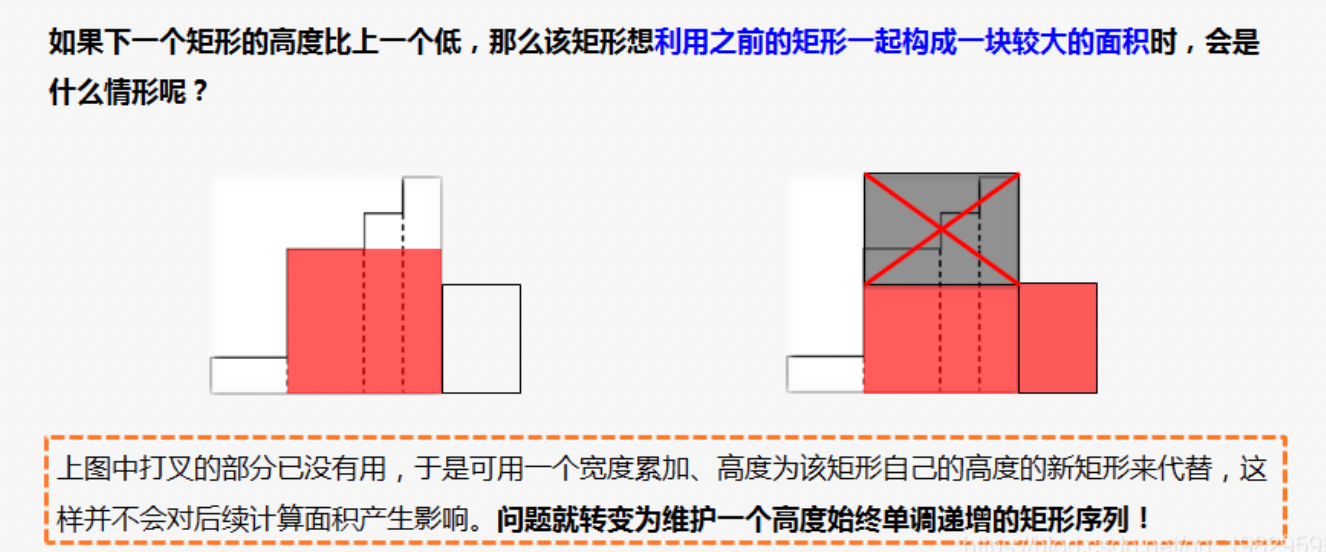
   ```cpp

   include

   using namespace std; typedef long long ll; const int N=100010; int n, h[N], s[N], w[N], top; long long res; int main(){ while(~scanf(“%d”, &n)){ if(n == 0) break; top = 0; for(int i=1;i<=n;i++){ scanf(“%d”, &h[i]); } h[n+1] = top = res = 0; for(int i=1;i<=n+1;i++){ if(h[i] > s[top]) {

    s[++top] = h[i];
    w[top] = 1;

   } else {

    int width = 0;
    while(s[top] > h[i]) {
      width += w[top];
      res = max(res, 1ll * width * s[top]);
      top --;
    }
    s[++top] = h[i];
    w[top] = width + 1;

   } } cout << res << endl; } }

```