1. 第一课

课程重点在于图的预测模型(predictive models of graphs)

网络和图

听完课之后发现以前对图和网络的区别没理解明白，由于是先接触图后来才了解到网络，认为网络是图的一个泛化概念。

通过slides理解到，网络是一种更加广泛的概念，而图是对其的压缩抽象，虽然两者的区别有时也是模糊的。网络可以认为是自然图，通常具有较大规模，隐藏着一些系统的规律和特性；而图的概念可以是信息图，是经过压缩提取的信息、知识结构。

简而言之，Networks: Natural Graphs; Graphs: Information Graphs.

网络分析任务/方式：

节点分类。预测给定节点的种类
链路预测。预测两节点间是否有连接
社区检测。检测节点的密集型连接群
网络相似性检测。测量两个节点或网络的相似性

网络：知识网络(Knowledge Graphs)、异质网络(Heterogeneous Graphs)、多模型网络(Multimodal Graphs)

网络类型：

Social networks;
Economic networks;
Communication networks;
Information networks: Web & citations;
Internet;
Networks of neurons;
…

结构基础知识

对于网络，属性名称为network, node, link，而对于图，属性名称为Graph, vertex, edge.

无向图、有向图、带权图、无权图、连通图、极大连通分量、强连通图（有向图中，每对节点间都存在着相互的路径）、弱连通图（）、节点的度、入度、出度、完全图、邻接矩阵、边集、邻接列表、二分图（Bipartite graph，有两个点集 $图机器学习(CS224W) - 图1$ ，边只存在两点集的元素之间，同一点集内的元素间不存在边）

通常网络之中，大部分项都是0元素，导致网络极其稀疏，使得网络的表示方式显得尤为重要。

谱方法

拉普拉斯矩阵

是对图的一种表示，组合了度矩阵和邻接矩阵，即为 $图机器学习(CS224W) - 图2$

$图机器学习(CS224W) - 图3$

$图机器学习(CS224W) - 图4$ 为度矩阵，是一个对角方阵，对角线上的元素值是该点的度数。拉普拉斯矩阵对角线上元素为该点的度数，非对角线元素为从一点到另一点的边的权重（无边为0）的负值。

规范化拉普拉斯矩阵

首先介绍规范化邻接矩阵（ $图机器学习(CS224W) - 图5$ 为第 $图机器学习(CS224W) - 图6$ 个节点的度）：

$图机器学习(CS224W) - 图7$

由于度矩阵为对角矩阵，有 $图机器学习(CS224W) - 图8$ ，于是 $图机器学习(CS224W) - 图9$ ，规范化的拉普拉斯矩阵为：

$图机器学习(CS224W) - 图10$ D%5E%7B-1%2F2%7D%20%5C%5C%5C%5C%0A%26%3D%20I%20-%20D%5E%7B-1%2F2%7DAD%5E%7B-1%2F2%7D%0A%5Cend%7Balign%7D%0A#card=math&code=%5Cbegin%7Balign%7D%0A%5Chat%20L%20%26%3D%20D%5E%7B-1%2F2%7DLD%5E%7B-1%2F2%7D%20%5C%5C%5C%5C%0A%26%3D%20D%5E%7B-1%2F2%7D%28D-A%29D%5E%7B-1%2F2%7D%20%5C%5C%5C%5C%0A%26%3D%20I%20-%20D%5E%7B-1%2F2%7DAD%5E%7B-1%2F2%7D%0A%5Cend%7Balign%7D%0A)

8. 图神经网络

学习网络中节点的低维向量表示。

目标： $图机器学习(CS224W) - 图11$ %20%5Capprox%20z_v%5ETz_u#card=math&code=similarity%28u%2Cv%29%20%5Capprox%20z_v%5ETz_u)

浅层模型学习到的是节点的embedding查找表。本身具有如下限制：

需要 $图机器学习(CS224W) - 图12$ #card=math&code=O%28%5Cvert%20N%5Cvert%29)参数
transductive，只能产生参入训练的节点的向量表示
没有利用到节点的特征

图神经网络的特点是：对节点的编码是图结构的多层非线性变换。

朴素的办法是采用全连接层网络，然后把增加特征列的邻接矩阵每行输入到网络中，这种方法有几个问题：

具有 $图机器学习(CS224W) - 图13$ #card=math&code=O%28n%29)参数
不适用各种大小的图（神经网络的输入数量是固定的，不同大小的图具有不同的节点数量，导致邻接矩阵规模不一）
对节点的排序不是固定的

图神经网络的基本设定

属性

节点集： $图机器学习(CS224W) - 图14$
邻接矩阵： $图机器学习(CS224W) - 图15$
节点属性矩阵： $图机器学习(CS224W) - 图16$

不同类型的网络具有不同的节点属性，例如：

社交网络：用户信息、用户图片
生物网络：基因表达谱、基因功能信息

聚合局部网络

定义聚合策略
定义计算图

堆叠多层网络

设计模型、参数、损失函数、训练方式
拟合模型

GCN

思想

邻节点定义了节点的计算图。每个节点的信息是通过自身信息和邻节点传播过来的信息组合而成的。重点是如果进行在图上进行信息的传播，计算节点特征。（Based on local network neighborhoods）。通常传播深度控制在4-5跳，根据六度分离理论，通过6各节点就可以访问到图上任何一个节点。

步骤：

定义节点的计算图
通过计算图传播、变换信息

聚合方式

核心操作是对于邻节点的聚合方式，对于邻节点的聚合应该是不区分节点次序的（order invariant）。。聚合方式有多种，比如平均化，如下：（初始化为节点的初始特征表示， $图机器学习(CS224W) - 图17$ 为训练参数）

$图机器学习(CS224W) - 图18$ %7D%5Cfrac%7Bhu%5E%7Bk-1%7D%7D%7B%5Cvert%20N(v)%5Cvert%7D%2BB_kh_v%5E%7Bk-1%7D)%5C%5C%5C%5C%0A%26z_v%20%3D%20h_v%5EK%0A%5Cend%7Balign%7D%0A#card=math&code=%5Cbegin%7Balign%7D%0A%26h_v%5E0%20%3D%20x_v%5C%5C%5C%5C%0A%26h_v%5Ek%20%3D%20%5Csigma%28W_k%20%5Csum%7Bu%20%5Cin%20N%28v%29%7D%5Cfrac%7Bh_u%5E%7Bk-1%7D%7D%7B%5Cvert%20N%28v%29%5Cvert%7D%2BB_kh_v%5E%7Bk-1%7D%29%5C%5C%5C%5C%0A%26z_v%20%3D%20h_v%5EK%0A%5Cend%7Balign%7D%0A)

上式的状态转移的等价向量形式（ $图机器学习(CS224W) - 图19$ 为图的度矩阵）：

$图机器学习(CS224W) - 图20$ %7DW_0%5E%7B(l)%7D%2B%5Chat%20AH%5E%7B(l)%7DW_1%5E%7B(l)%7D)%5C%5C%5C%5C%0A%26%5Chat%20A%20%3D%20D%5E%7B(-%5Cfrac%7B1%7D%7B2%7D)%7DAD%5E%7B-%5Cfrac%7B1%7D%7B2%7D%7D%0A%5Cend%7Balign%7D%0A#card=math&code=%5Cbegin%7Balign%7D%0A%26H%5E%7Bl%2B1%7D%20%3D%20%5Csigma%28H%5E%7B%28l%29%7DW_0%5E%7B%28l%29%7D%2B%5Chat%20AH%5E%7B%28l%29%7DW_1%5E%7B%28l%29%7D%29%5C%5C%5C%5C%0A%26%5Chat%20A%20%3D%20D%5E%7B%28-%5Cfrac%7B1%7D%7B2%7D%29%7DAD%5E%7B-%5Cfrac%7B1%7D%7B2%7D%7D%0A%5Cend%7Balign%7D%0A)

另外还有其它的聚合方式（GraphSAGE提出），通用型的聚合表示为 $图机器学习(CS224W) - 图21$ #card=math&code=AGG%28%29)：

$图机器学习(CS224W) - 图22$ %7D%2C%20%5Cforall%20u%5Cin%20N(v)%7D)%20%2B%20B_kh_v%5E%7B(k-1)%7D%20%5Cbig%5D)%0A#card=math&code=h_v%5Ek%20%3D%20%5Csigma%5Cbig%28%5BW_k%5Ccdot%20AGG%28%7Bh_u%5E%7B%28k-1%29%7D%2C%20%5Cforall%20u%5Cin%20N%28v%29%7D%29%20%2B%20B_kh_v%5E%7B%28k-1%29%7D%20%5Cbig%5D%29%0A)

MEAN。平均化各邻节点的表示，即上面提到的， $图机器学习(CS224W) - 图23$ %7D%5Cfrac%7Bhu%5E%7Bk-1%7D%7D%7B%5Cvert%20N(v)%5Cvert%7D#card=math&code=AGG%3D%5Csum%7Bu%20%5Cin%20N%28v%29%7D%5Cfrac%7Bh_u%5E%7Bk-1%7D%7D%7B%5Cvert%20N%28v%29%5Cvert%7D)
POOL。池化，一般也就还是平均池化和最大化池化，其中平均池化不同于MEAN操作，池化是先将邻节点逐个转换（ $图机器学习(CS224W) - 图24$ %7D#card=math&code=Qh_u%5E%7B%28k-1%29%7D)）之后在进行操作。
LSTM。使用LSTM处理邻节点，由于要保持邻节点的次序无关性，可将邻节点序列多次打乱后多次输入。 $图机器学习(CS224W) - 图25$ %7D%2C%20%5Cforall%20u%20%5Cin%20%5Cpi(N(v))%5D)#card=math&code=AGG%3DLSTM%28%5Bh_u%5E%7B%28k-1%29%7D%2C%20%5Cforall%20u%20%5Cin%20%5Cpi%28N%28v%29%29%5D%29)

原始空间域GCN和GraphSAGE的差别就在于聚合函数，GraphSAGE采用了更加通用性的聚合函数设定。

谱域GCN则略有差别，通过稀疏矩阵的计算，比如如下两种形式：

$图机器学习(CS224W) - 图26$
$图机器学习(CS224W) - 图27$

损失函数

损失函数取决于训练类型和具体目标。对于无监督学习，损失函数可以同此前的非监督方法：

随机游走方法（node2vec, DeepWalk, struc2vec）
图分解
节点相似性

而对于监督学习，可采用交叉熵作为损失函数，如：

$图机器学习(CS224W) - 图28$ )%2B(1-yv)%5Clog(1-%5Csigma(z_v%5ET%5Ctheta))%0A#card=math&code=%5Cmathcal%20L%20%3D%20%5Csum%7Bv%5Cin%20V%7Dy_v%5Clog%28%5Csigma%28z_b%5ET%5Ctheta%29%29%2B%281-y_v%29%5Clog%281-%5Csigma%28z_v%5ET%5Ctheta%29%29%0A)

GAT

在GCN中，聚合邻节点时将每个邻节点视为同等重要，如果通过引入注意力机制将其赋予不同的权重，则有了GAT。权重通过 $图机器学习(CS224W) - 图29$ 函数计算：

$图机器学习(CS224W) - 图30$ %7D%7B%5Csum%7Bk%5Cin%20N(v)%7D%5Cexp(e%7Bvk%7D)%7D%5C%5C%5C%5C%0Ahv%5Ek%20%3D%20%5Csigma(%5Csum%7Bu%5Cin%20N(v)%7D%5Calpha%7Bvu%7DW_kh_u%5E%7Bk-1%7D)%0A#card=math&code=%5Calpha%7Bvu%7D%3D%5Cfrac%7B%5Cexp%28e%7Bvu%7D%29%7D%7B%5Csum%7Bk%5Cin%20N%28v%29%7D%5Cexp%28e%7Bvk%7D%29%7D%5C%5C%5C%5C%0Ah_v%5Ek%20%3D%20%5Csigma%28%5Csum%7Bu%5Cin%20N%28v%29%7D%5Calpha_%7Bvu%7DW_kh_u%5E%7Bk-1%7D%29%0A)

为了稳定注意力机制的学习过程，可以使用多头注意力(Multi-head attention)机制：对于给定层的注意力机制，将注意力机制独立进行多次，每次采用不同的参数，然后将整个结果聚合起来。

应用

PinSAGE，基于Pinterest平台的内容推荐，基于图信息辅助矫正CNN对图片的识别结果。

GNN类别

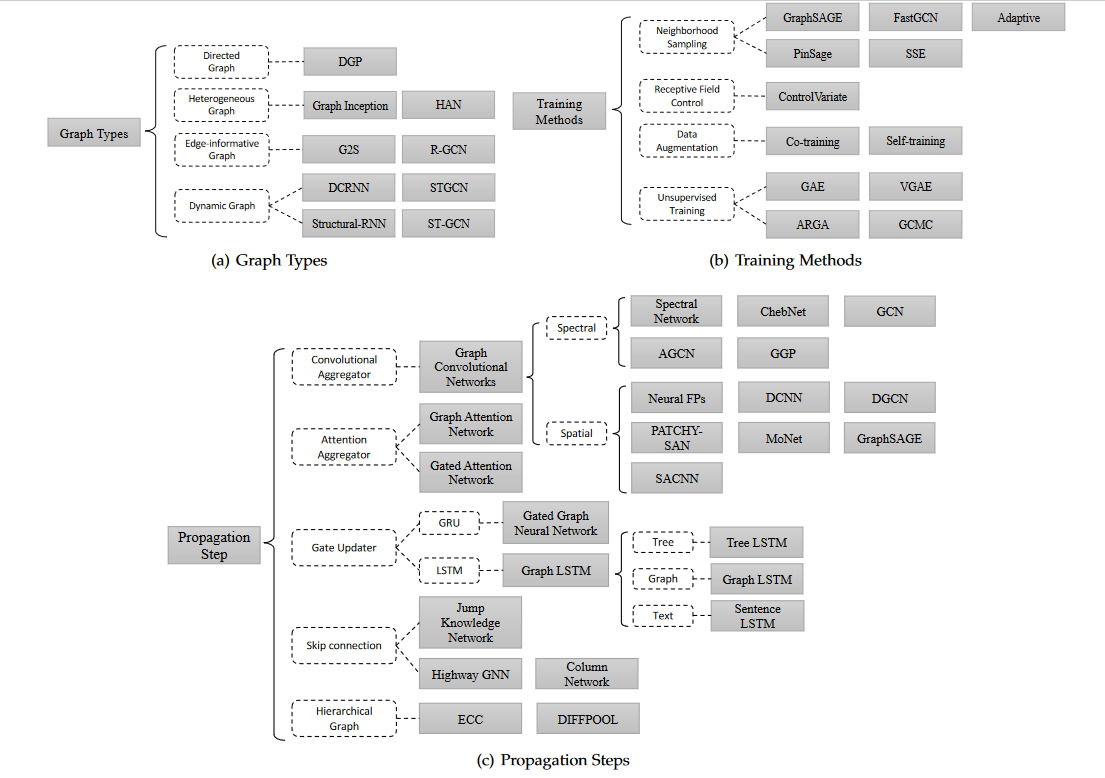
SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS