1.1 GEMM 算法基础

GEMM（General Matrix Multiplication），通用矩阵乘法。
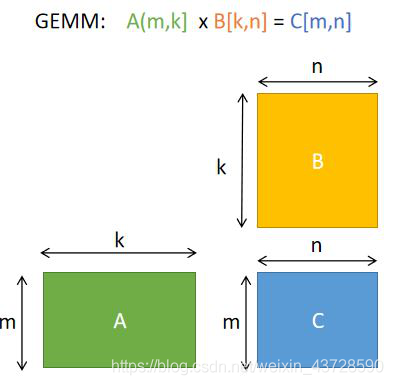
GEMM矩阵相乘优化 - 图1

则根据矩阵相乘的定义，可得 C=AB+C 的计算公式为：
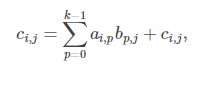
GEMM矩阵相乘优化 - 图2

从而可实现为：

  1. for i=0:m-1
  2.     for j=0:n-1
  3.         for p=0:k-1
  4.             C(i,j):=A(i,p)*B(p,j)+C(i,j)
  5.         endfor
  6.     endfor
  7. endfor

可以看出，根据定义实现的算法计算复杂度为 O(mnk)，也就是 O(n^3)。

1.2 GEMM 算法优化

1.2.1 循环重排充分利用缓存

应该首先注意到我们访问数据的模式。我们按照下图 A 的形式逐行遍历数据，按照下图 B 的形式逐列遍历数据。
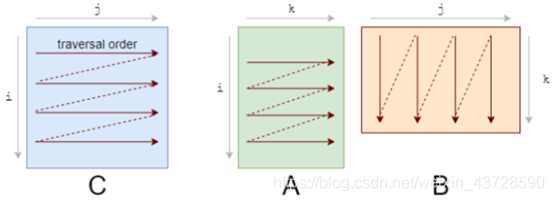
GEMM矩阵相乘优化 - 图3

它们的存储也是行优先的，因此一旦我们找到 A[i, k]，则它在该行中的下一个元素 A[i, k+1] 已经被缓存了。接下来我们来看 B 中发生了什么：

列的下一个元素并未出现在缓存中，即出现了缓存缺失（cache miss）。这时尽管获取到了数据，CPU 也出现了一次停顿。获取数据后，缓存同时也被 B 中同一行的其他元素填满。我们实际上并不会使用到它们，因此它们很快就会被删除。多次迭代后，当我们需要那些元素时，我们将再次获取它们。我们在用实际上不需要的值污染缓存。

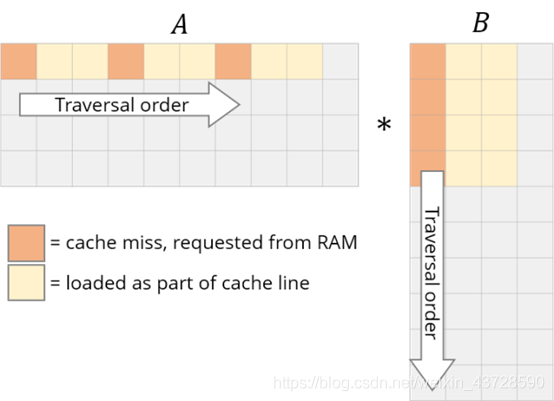
GEMM矩阵相乘优化 - 图4

我们需要重新修改 loop，以充分利用缓存能力。如果数据被读取，则我们要使用它。这就是我们所做的第一项改变：循环重排序（loop reordering）。

我们将 i,j,k 循环重新排序为 i,k,j：

  2. for i in0..M: 
  3.     for k in0..K: 
  4.         for j in0..N:

答案仍然是正确的，因为乘 / 加的顺序对结果没有影响。而遍历顺序则变成了如下状态：
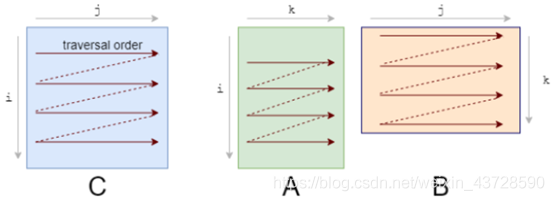
GEMM矩阵相乘优化 - 图5

循环重排序这一简单的变化，却带来了相当可观的加速。

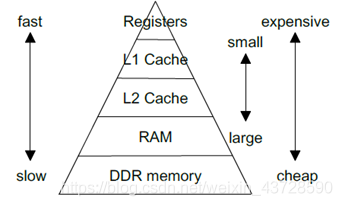
1.2.2 平铺（Tiling）充分利用缓存

要想进一步改进重排序，我们需要考虑另一个缓存问题。

对于 A 中的每一行，我们针对 B 中所有列进行循环。而对于 B 中的每一步，我们会在缓存中加载一些新的列，去除一些旧的列。当到达 A 的下一行时，我们仍旧重新从第一列开始循环。我们不断在缓存中添加和删除同样的数据，即缓存颠簸（cache thrashing）。

如果所有数据均适应缓存，则颠簸不会出现。如果我们处理的是小型矩阵，则它们会舒适地待在缓存里，不用经历重复的驱逐。庆幸的是，我们可以将矩阵相乘分解为子矩阵。要想计算 C 的 r×c 平铺，我们仅需要 A 的 r 行和 B 的 c 列。接下来，我们将 C 分解为 6x16 的平铺：

  1. C(x, y) += A(k, y) * B(x, k);
  2. C.update().tile(x, y, xo, yo, xi, yi, 6, 16)

我们将 x,y 维度分解为外侧的 xo,yo 和内侧的 xi,yi。我们将为该 6x16 block 优化 micro-kernel（即 xi,yi），然后在所有 block 上运行 micro-kernel（通过 xo,yo 进行迭代）。

1.2.3 展开（Unrolling）

循环使我们避免重复写同样代码的痛苦，但同时它也引入了一些额外的工作，如检查循环终止、更新循环计数器、指针运算等。如果手动写出重复的循环语句并展开循环，我们就可以减少这一开销。例如，不对 1 个语句执行 8 次迭代，而是对 4 个语句执行 2 次迭代。

这种看似微不足道的开销实际上是很重要的，最初意识到这一点时我很惊讶。尽管这些循环操作可能「成本低廉」，但它们肯定不是免费的。每次迭代 2-3 个额外指令的成本会很快累积起来，因为此处的迭代次数是数百万。随着循环开销越来越小，这种优势也在不断减小。

1.2.4 内存对齐

内存对齐的原则：任何 K 字节的基本对象的地址必须都是 K 的倍数。

假设 cache line 为 32B。待访问数据大小为 64B，地址在 0x80000001，则需要占用 3 条 cache 映射表项；若地址在 0x80000000 则只需要 2 条。内存对齐变相地提高了 cache 命中率。

1.2.5 向量化

大部分现代 CPU 支持 SIMD（Single Instruction Multiple Data，单指令流多数据流）。在同一个 CPU 循环中，SIMD 可在多个值上同时执行相同的运算 / 指令（如加、乘等）。如果我们在 4 个数据点上同时运行 SIMD 指令，就会直接实现 4 倍的加速。
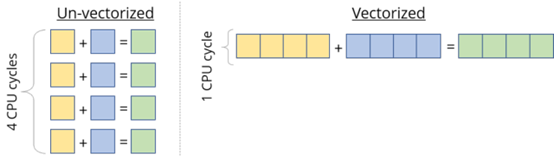
GEMM矩阵相乘优化 - 图6

使用 FMA（Fused Multiply-Add）。尽管乘和加是两种独立的浮点运算，但它们非常常见，有些专用硬件单元可以将二者融合为一，作为单个指令来执行。编译器通常会管理 FMA 的使用。

1.2.6 矩阵分块

充分利用多核性能。

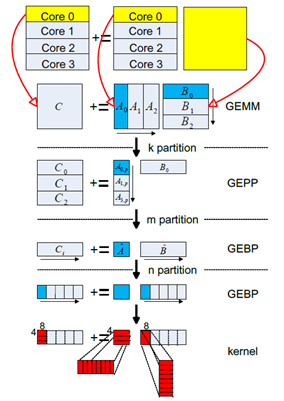
GEMM 的分块方式：
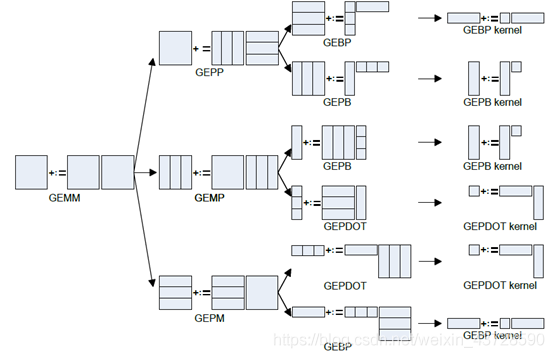
GEMM矩阵相乘优化 - 图7

图中共有 6 中拆分方法，依次分析：

  1. 拆分 K，A 矩阵拆成多列，B 矩阵拆成多行。拆分 M，A 的一列拆分成三个 block。拆分 N，B 的一行也可以拆分成多个小 slice，每个 slice 放到寄存器中。遍历 A 的列，A 的每个 block 乘以 B 的一行，得到矩阵 C 的一行的部分值。 拆分之后 Aip 为 (mc, kc), Bpj 为 (kc, nr), Cij 为 (mc, nr)。
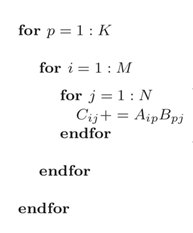
    GEMM矩阵相乘优化 - 图8
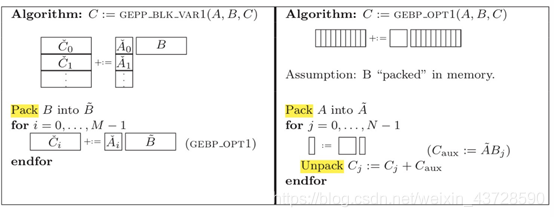
    GEMM矩阵相乘优化 - 图9
    如果 kc*mc 很小，那么 Aip、Bpj、Cij 都放入 cache 中，Aip（A 矩阵的一个 block）只需要被加载进 cache 一次，提高了 cache 命中率。对 Ai 和 Bj 进行 pack 使其内存连续。由于处理 B 矩阵是按照每个 slice 依次进行，所以这种划分更适合于列存储优先的矩阵乘。

  2. 拆分 K，A 拆分成多列，B 拆成多行。拆分 N，B 的一行被拆分为三个 block。拆分 M，A 的一列被拆分为多个 slice。A 的一列乘以 B 的每个 block，得到矩阵 C 的一列的部分值。
    GEMM矩阵相乘优化 - 图10
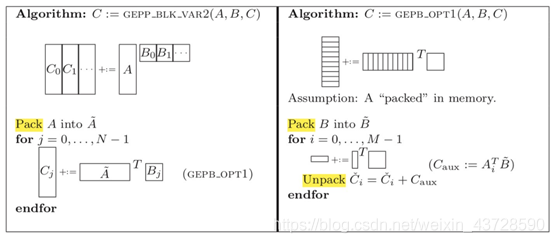
    GEMM矩阵相乘优化 - 图11
    类似于 (1), 只是变成 A 的一行乘以 B 的一个 block。所以这种划分更适合于行存储优先的矩阵乘。

  3. 拆分 N，B 矩阵被拆分为多列。再拆分 K，A 拆分成多列，B 拆成多个 block。拆分 M，A 的一列被拆分为多个小 block。A 的一列乘以 B 的每个 block，得到矩阵 C 的一列的部分值。
    GEMM矩阵相乘优化 - 图12
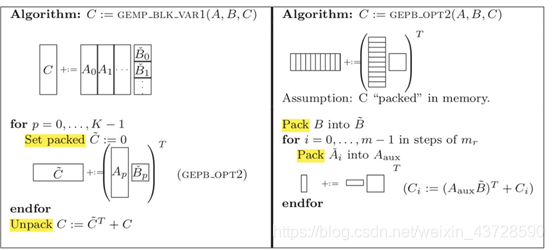
    GEMM矩阵相乘优化 - 图13
    这种划分与 (2) 的划分唯一的区别是，访问 B 矩阵是按列还是按行。很显然 (2) 的划分方式好于 (3)。

  4. 类似于普通矩阵乘，A 的一行*B 的一列。然后在 K 拆分，将 A 矩阵的每行划分为多个 block, 将 B 矩阵的每列划分为多个 block。
    GEMM矩阵相乘优化 - 图14
    每次执行可以得到 C 矩阵一个 block 的值。当 MNK 非常大时，cache 无法存下 Cj，所以划分方法没有什么优势。

  5. 类似于 (4), 都是每次执行可以得到 C 矩阵的一个 block 的值。同样当 MNK 非常大时，cache 无妨存下 Cj，所以该方法没有什么优势。
    GEMM矩阵相乘优化 - 图15

  6. 类似于（1）。不一样在于：对 A 矩阵的 block 遍历是按行访问。和（1）相比，最外层循环是 i，而非 p。遍历顺序为 A0B0 + A1_B1 + … + Ap_Bp 才能得到 C 一行的最终值，因此需要不断的更新 C 这一行的值，可以使用一个顺序的 cache 数组存放 pack ，最后在 unpack 的时候累加。这与 (1) 中的按列访问 A 矩阵的 block 不同,（1) 中 Ci += Ai, 在最内层循环时只需要使用寄存器存储每次 Ai*Bpj 的结果。
    GEMM矩阵相乘优化 - 图16
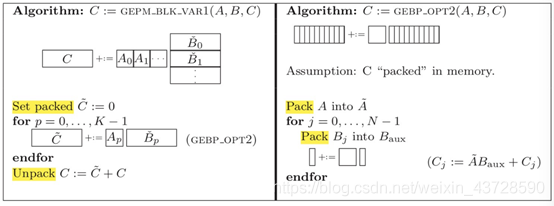
    GEMM矩阵相乘优化 - 图17
    由于在循环外 cache 级别 unpack C 远复杂于在循环内 register 级别 unpack C，因此 (1) 比 (6) 好。

1.2.7 双缓冲

计算的同时在不同级的存储介质中进行数据搬移，隐藏访存开销
GEMM矩阵相乘优化 - 图18

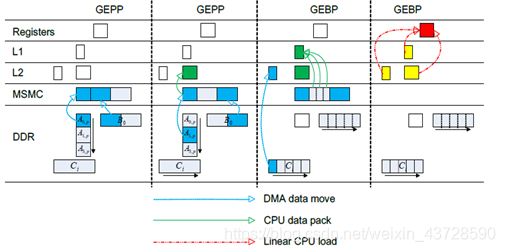
GEMM矩阵相乘优化 - 图19

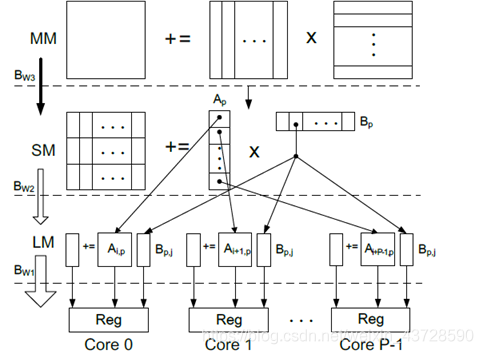
将矩阵分块同时利用不同核进行计算，充分利用多核性能
GEMM矩阵相乘优化 - 图20

GEMM矩阵相乘优化 - 图21

2.1 计算卷积的方法

计算卷积的方法有很多种，常见的有以下几种方法：

  • 滑窗：这种方法是最直观最简单的方法。 但是，该方法不容易实现大规模加速，因此，通常情况下不采用这种方法（但是也不是绝对不会用，在一些特定的条件下该方法反而是最高效的）。
  • im2col：目前几乎所有的主流计算框架包括 Caffe, MXNet 等都实现了该方法. 该方法把整个卷积过程转化成了 GEMM 过程，而 GEMM 在各种 BLAS 库中都是被极致优化的，一般来说，速度较快。
  • FFT：傅里叶变换和快速傅里叶变化是在经典图像处理里面经常使用的计算方法，但是，在 ConvNet 中通常不采用，主要是因为在 ConvNet 中的卷积模板通常都比较小，例如 3×3 等，这种情况下，FFT 的时间开销反而更大，所以很少在 CNN 中利用 FFT 实现卷积。
  • Winograd： Winograd 是存在已久最近被重新发现的方法，在很多场景中, Winograd 方法都显示出较大的优势，目前 cudnn 中计算卷积就使用了该方法。

2.2 Img2col

2.2.1 CNN 中张量的存储

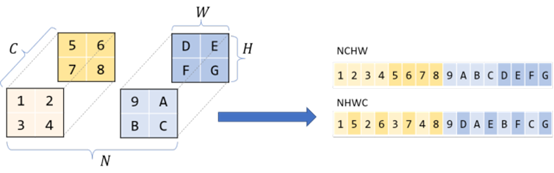
通常张量（如 CNN 中的张量）的存储顺序是 NCHW、NHWC 等。

NCHW 存储顺序，即如果 HxW 图像的 block 为 N，通道数为 C，则具备相同 N 的所有图像是连续的，同一 block 内通道数 C 相同的所有像素是连续的
GEMM矩阵相乘优化 - 图22

2.2.2 卷积运算转化为 GEMM

卷积是滤波器和输入图像块（patch）的点乘。如果我们将滤波器展开为 2-D 矩阵，将输入块展开为另一个 2-D 矩阵，则将两个矩阵相乘可以得到同样的数字。与 CNN 不同，近几十年来矩阵相乘已经得到广泛研究和优化，成为多个科学领域中的重要问题。将图像块展开为矩阵的过程叫做 im2col（image to column）。我们将图像重新排列为矩阵的列，每个列对应一个输入块，卷积滤波器就应用于这些输入块上。

下图展示了一个正常的 3x3 卷积：
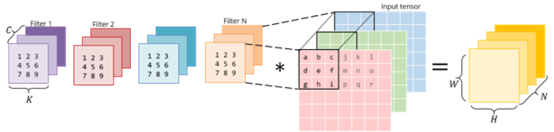
GEMM矩阵相乘优化 - 图23

下图展示的是该卷积运算被实现为矩阵相乘的形式。右侧的矩阵是 im2col 的结果，它需要从原始图像中复制像素才能得以构建。左侧的矩阵是卷积的权重，它们已经以这种形式储存在内存中。
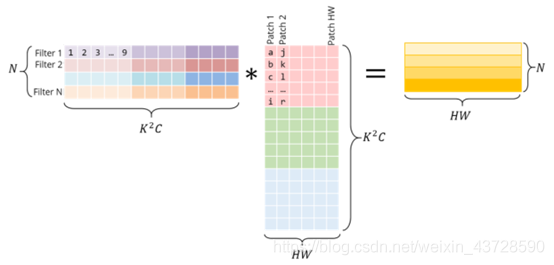
GEMM矩阵相乘优化 - 图24

出于视觉简洁考虑，此处将每个图像块作为独立的个体进行展示。而在现实中，不同图像块之间通常会有重叠，因而 im2col 可能导致内存重叠。生成 im2col 缓冲（im2col buffer）和过多内存（inflated memory）所花费的时间必须通过 GEMM 实现的加速来抵消。

使用 im2col 可以将卷积运算转换为矩阵相乘。现在我们可以使用更加通用和流行的线性代数库（如 OpenBLAS、Eigen）对矩阵相乘执行高效计算，而这是基于几十年的优化和微调而实现的。
https://blog.csdn.net/weixin_43728590/article/details/107212069

https://blog.csdn.net/weixin_43728590/article/details/107212069