深度学习轻量级推理及加速 - 神经网络量化方法 - 《Machine Learning》

背景介绍
TensorRT 量化方法
IAO 量化方法
总结
- 参考资料

神经网络虽然在多个领域取得了非常巨大的成就，但是其本质是大量参数的拟合和泛化，如果想处理更加复杂的任务，在没有过拟合的情况下，增加训练数据和加大网络规模无疑是简单有效的手段。现实情况就是这么做的，但是巨大的参数量和复杂的网络结构造成了两个主要的问题：模型体积和运算速度。这两个问题会带来诸如内存容量，内存存取带宽，移动端还有电量消耗等一系列问题，大大限制了神经网络的应用场景。

背景介绍

为了解决这些问题，目前的研究方向主要就是两方面：一是精心设计小巧而有效的网络结构取代大网络模型，二是通过压缩和编码的方式直接减小现有网络的规模。量化就是一种很好的压缩和编码方式，量化的目的很简单，就是减小存储体积和加速运算，有效解决神经网络的根本问题，并且在实际的一些应用中表现出色，也是目前采用最广泛的压缩和编码方式。如果在一些小巧的网络中再使用量化，就可以进一步压缩和加速网络，使其能够移植到移动端，例如，TensorFlow 量化的 MobileNetV1 仅为 4.8 MB，这甚至比大多数 GIF 动图还要小，从而可以轻松地部署在任何移动平台上。

量化简单来说就是使用一种低精度的方式来作为存储和计算的数值表示方式。一般而言，在神经网络构建和训练时使用 float，也就是 FP32 作为一种通用的数据表示方式。量化使用 FP16（半精度浮点），INT8/UINT8（8 位的定点整数）等低精度数值格式来存储以及计算，目前低精度往往都是指 INT8/UINT8。当然，存储和计算并不是严格要保持一致的，有些参数或操作符必须采用 FP32 格式才能保持准确度，因此还有一种混合精度的表示方式，TensorRT 中就使用了这种计算方式。也有一些更加特殊的量化方式，二进制（0，1）、三元量化（-1，0，+1）、4 位整数等等，这些特殊的方式可以在一些特殊的网络中应用，用于进一步压缩，不过本文不对这些方法进行表述，有兴趣可以查阅这篇关于模型压缩和加速的综述。因为不同精度数值表示的范围和单位数值都不一样（如下表所示），因此我们必须做点什么来减少这种精度损失。

	Dynamic Range	Min Positive Value
FP32	-3.4x10^38 ~ +3.4x10^38	1.4x10^-45
FP16	-65504 ~ +65504	5.95x10^-8
INT8	-128 ~ +127	1

本文将简要介绍目前应用最为广泛的 NVIDIA 的 TensorRT 和 Google 的 IAO 量化方法，这两个量化方法都属于 8-bit 量化，其本质原理是类似的，只不过在一些实际应用操作上面，各有自己的理解和不同。

TensorRT 量化方法

神经网络的计算主要集中在卷积层和全连接层，量化也是针对这两个层做的。这两个层的计算都是可以表示为：output = input * weights + bias。因为现在的深度学习框架会将卷积和全连接层的计算都打包成矩阵相乘的形式，因此大量的计算都集中在矩阵相乘上了。TensorRT 的量化思路就是用 INT8 代替 FP32 进行两个矩阵相乘计算。

TensorRT 量化原理

TensorRT 的线性量化公式：

Tensor Values = FP32 scale factor * INT8 array + FP32 bias

在这个量化公式中，FP32 数值（Tensor Values）被表示成 INT8 数值（INT8 array）乘以量化因子加上一个量化偏，两个参数均为 FP32 类型。因此，利用上述的公式可以表示神经网络中两个矩阵相乘：

A = scale_A * QA + bias_A
B = scale_B * QB + bias_B
A * B = scale_A * scale_B * QA * QB + scale_A * QA * bias_B + scale_B * QB * bias_A + bias_A * bias_B

NVIDIA 研究人员通过实现发现，其实我们并不需要在量化的时候加上偏置。我理解主要是因为偏置对于一组数值而言，其改变的是数值的分布位置，但是当前神经网络的归一化操作很多，因此可以去掉偏置。当然了，实验出的结果更有说服力。因此两个矩阵相乘的量化表示可以简化为：

A * B = scale_A * scale_B * QA * QB

这样就很明显了，只要我们有两个矩阵的 scale 以及量化后的矩阵，我们就可以表示其 FP32 的相乘结果。而量化后的矩阵就是 FP32 除以 scale 得到的，FP32 的数值是已知的（训练好的参数或者输入），因此量化的问题就变成了如何得到量化参数 scale factor。

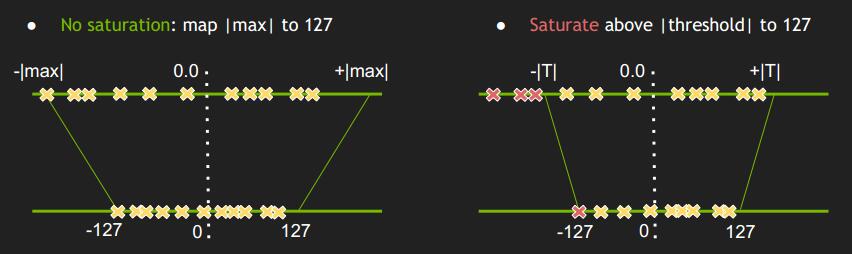
既然是相乘，我们首先想大了线性映射，线性映射就是找一个值除以 INT8 的最大值，就可以求得 scale factor。TensorRT 介绍关于这个线性映射倍数的求解方法，有两种不同的方式：

非饱和映射：找到这组 FP32 数值的绝对值最大值 |max| 作为 FP32 的映射最大值
饱和映射：通过其他方法找到一个更加合适的阈值 T<=|max| 作为 FP32 的映射最大值

很明显，如果数值分布不够集中，比如有一些奇异点（很大或者很小），非饱和映射导致 scale factor 偏大，因为 INT8 单位精度远小于 FP32，就会让 FP32 中很多数集中在 INT8 的某几个数字上，带来了严重的精度影响。因此 TensorRT 采用了饱和映射，并且使用 KLD（KL 散度）方法寻找阈值 T。下图是 NVIDIA 官方 PPT 中对一些网络的激活值的分布的统计：

KLD

FP32 用 INT8 表示，本质就是一种再编码，这个学过通信技术的同学可能会容易理解。对于两种不同的编码方式，可以采用一种称为交叉熵的方式计算二者的差异性，本文并不想过多的着墨于信息论中关于信息熵的这些知识，这些知识通过搜索引擎可以获取，只介绍相关知识。

首先是信息熵，对于一种编码，其是符号的集合，每种符号都有其出现的概率，信息熵的大小可以表示为：

H(X,p)=−∑x∈Xp(x)log⁡p(x)

其中 p(x) 是符号出现的概率，−log⁡p(x) 就是这个符号的信息，这就是信息论的核心和理论基础，信息的表示。−log⁡p(x) 也可以看作是每个符号的编码长度，因此信息熵也可以表示编码长度的期望。

当我们使用另一种编码 q(x) 方式去表示这个信息，求得编码长度的期望称之为交叉熵：

H(X,p,q)=−∑x∈Xp(x)log⁡q(x)

一般而言，信息熵是最优编码，因此其编码期望就是最小编码长度，因此交叉熵必然是大于等于信息熵，我们可以计算两种不同编码表示的长度期望的差异，也是两个信息熵的差值：

D(p||q)=H(X,p,q)−H(X,p)=−∑x∈Xp(x)(log⁡q(x)−log⁡p(x))

上述两个信息熵的差值称之为相对熵，KLD 就是使用相对熵来描述两个不同数值分布的差异性。如果想要量化某一组数值，其具体做法如下：

准备一个校准数据集，覆盖模型的使用场景即可，数量不需要很多。
将数据集的每张图片都通过模型做一次预测，在这个过程中，对所有要量化的层的 FP32 数值分布进行统计，得到 |max|。
- 量化是针对每个 channel 单独做的，因此卷积层的每个 channel 都是单独统计、计算和量化的，后续操作也是。
将 0~|max| 分成 n 个 bin，然后再次遍历所有图片，让每个量化层中的数值落到其属于的 bin 中，统计每个 bin 的数目。
- |max| / n 就可以得到每个 bin 的宽度 w，因此就分为了 0~w, w|max| 总共 n 个 bin。
- 对每个数值按照其绝对值分到不同 bin 中。
- TensorRT 官方使用的 n 是 2048，mxnet 是 4096，n 越大越好，但是计算量会上升。
遍历第 128~n 个 bin：
- 以当前 bin 的中值作为阈值 T，在其上做截断，将大于当前 bin 以外的 bin 的统计数目加到当前 bin 上，这一步是为了减少直接抹去这些数值带来的影响；
- 计算此时的概率分布 P，每个 bin 的概率就是其统计数目除以数值的总数；
- 创建一个新的编码 Q，其长度是 128，其元素的值就是 P 量化后的 INT8 数值（正数是 0~+127，负数是 - 128~-1)；
- 因为 Q 分布只有 128 个编码，为了计算交叉熵，将其扩展到和 P 同样的长度；
- 计算 P 和 Q 的相对熵，记录当前相对熵和阈值 T
选择最小的相对熵和其对应阈值 T，计算 scale factor = T / 127
- 实际代码中使用的是 scale factor = 127 / T，这样 FP32 到 INT8 量化的时候可以使用乘法而不是除法。
对每个 bin，取其中值作为这个 bin 当前的 FP32 表示，然后除以 scale factor，然后四舍五入，就得到了其量化后的 INT8 数值，将这个 bin 中所有的 FP32 数值都映射为这个 INT8 表示的数。多个 bin 可能映射为同一个 INT8 数字。

上述流程就是 TensorRT 中寻找阈值和计算 scale factor 的流程，有几个点还需要注意：首先为什么阈值遍历要从 128 开始呢？因为 INT8 可以表示的整数个数（正值）有 128 个，小于这个数值则直接一一对应即可。其次如果扩展 q 分布呢？TensorRT 官方 PPT 的例子，据说是这样的：

P=[1 0 2 3 5 3 1 7]     // fp32 的统计直方图，T=8
// 假设只量化到两个 bins，即量化后的值只有 -1/0/+1 三种
Q=[1+0+2+3, 5+3+1+7] = [6, 16]
// P 和 Q 现在没法做 KL 散度，所以要将 Q 扩展到和 P 一样的长度
Q_expand = [6/3, 0, 6/3, 6/3, 16/4, 16/4, 16/4, 16/4] = [2 0 2 2 4 4 4 4]  // P 中有 0 时，不算在内
D = KL(P||Q_expand)  // 这样就可以做 KL 散度计算了

这个扩展的操作，就像图像的上采样一样，将低精度的统计直方图 (Q)，上采样的高精度的统计直方图上去 (Q_expand)。由于 Q 中一个 bin 对应 P 中的 4 个 bin，因此在 Q 上采样的 Q_expand 的过程中，所有的数据要除以 4。但若分布 P 中有 bin 值为 0 时，是不算在内的，所以 6 只需要除以 3。

以上内容很多细节都来自 NCNN，其使用了和 TensorRT 一样的量化机制，因为 TensorRT 不开源，细节不得知，因此只有通过 NCNN 代码来了解一些细节的实现。下面具体讲讲 NCNN 中量化的一些实现。

NCNN 量化实现

NCNN 主要对 conv 和 fc 的计算进行量化，具体就是对输入数据 input_data 和模型权重 weights 进行量化，实现的量化机制就是 TensorRT 的量化方法。我主要讲解 conv 层的量化实现。

首先是通过校准数据集生成量化表，这个量化表主要存放的就是量化的 scale factor，这个表的生成是离线的，量化表的实现在 ncnn2table.cpp 中。NCNN 将 weights 和 input_data 分开计算的 scale factor。

量化权重

对于 weights，NCNN 并没有通过 KLD 来寻找阈值，而是直接利用最大值来计算 scale factor，这个做法和 NVIDIA 官方 PPT 中的做法是一致的，其中也提到了 weights 不需要饱和量化，只需要非饱和量化。我猜测其原因是 weights 的数值分布比较集中。关于 weights 的 scale factor 计算可以查看 QuantNet::get_conv_weight_blob_scales 这个函数。这里贴出其核心逻辑：

for (int n=0; n<((ncnn::Convolution*)layer)->num_output; n++)
{
    const ncnn::Mat weight_data_n = ((ncnn::Convolution*)layer)->weight_data.range(weight_data_size_output * n, weight_data_size_output);
    const float *data_n = weight_data_n;
    float max_value = std::numeric_limits<float>::min();
    for (int i = 0; i < weight_data_size_output; i++)
        max_value = std::max(max_value, std::fabs(data_n[i]));
    if (quant_6bit)
        scales.push_back(31 / max_value);
    else
        scales.push_back(127 / max_value);
}

量化输入数据

可以看出，NCNN 居然还有 6-bit 量化。还有补充一点就是 weights 是固定的，因此 weights 的量化是可以离线做的，而且可以看出，对于卷积层，其按照 channel 数目（weight_data_size_output），每个 channel 分别量化。

weights 的量化比较简单，麻烦的是输入数据的量化。NCNN 是按需量化，也就是如果这一层需要量化，才会将输入的数据进行量化，这个输入的数据因为是在 inference 的时候才能拿到，所以不可能离线量化，只能在线。而且因为输入数据分布不规律（conv 和 fc 的输入来自上一层的激活值），因此需要用饱和量化，也就是 KLD 寻找最佳阈值，这一步如果放到 inference 在线操作，太耗时了，因此使用校准数据集去模拟 inference 行为，然后在这个过程中寻找最佳阈值，计算 scale factor，作为输入数据的量化尺度。每一层都只有一个输入数据的 scale factor，并且将其也保存在量化表中。这部分代码实现在 post_training_quantize 函数中。核心逻辑如下：

float QuantizeData::get_data_blob_scale()
{   
    normalize_histogram();
    threshold_bin = threshold_distribution(histogram);
    threshold = (threshold_bin + 0.5) * histogram_interval;
    scale = 127 / threshold;
    return scale;
}

使用量化计算

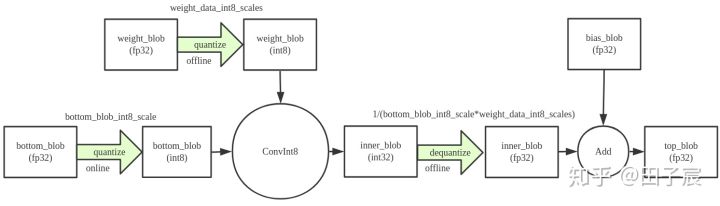
有了量化参数 scale factor，就可以使用它将 FP32 数值转换到 INT8 了。权重是已经离线量化好的，因此只需要将输入按照量化表中那个已经计算好的 scale factor 进行量化就可以了。NCNN 并不量化卷积层和全连接层的偏置项，因此需要将矩阵乘法得到的结果（INT32）反量化到 FP32，然后和 bias 做加法，输出到下一层。其中反量化也很简单，只需要使用权重和输入数据量化的 scale factor 乘积的倒数作为反量化的 scale factor 即可。计算流程图如下：

NCNN 中还有一些针对多个量化层的融合机制，简单来说就是当一个 Conv1 后面紧跟着另一个 Conv2 时，NCNN 会进行 requantize 的操作。大致意思就是在得到 Conv1 的 INT32 输出后，会顺手帮 Conv2 做量化，得到 Conv2 的 INT8 输入。这中间不会输出 FP32 的结果，节省一次内存读写。

针对具体的操作过程以及上图，都引自这篇文章，有兴趣可以查看。

IAO 量化方法

IAO 是 Google 提出的量化方法，主要应用在 TensorFlow Lite 中，有了 TensorRT 的知识铺垫，讲 IAO 就比较简单了。

IAO 量化原理

首先是量化公式：

Q=RS+Z

其中，R 表示真实的浮点值，Q 表示量化后的定点值，Z 表示 0 浮点值对应的量化定点值，也称零点漂移，S 则为量化的 scale factor，S 和 Z 的求值公式如下：

S=Rmax−RminQmax−Qmin

Z=Qmax−RmaxS

这里的 S 和 Z 均是量化参数，S 是 FP32 类型，而 Z 是 INT8 类型。 Q 和 R 均可由公式进行求值，不管是量化后的 Q 还是反推求得的浮点值 R，如果它们超出各自可表示的最大范围，那么均需要进行截断处理。

文章中指出 0 值对于神经网络具有重大意义，需要小心的处理，因此引入了零点偏移的概念。在我个人看来，我觉得这个量化公式和 TensorRT 中权重量化的区别就在于加入了 TensorRT 去掉的偏置项。虽然 NVIDIA 研究人员用实验说明了这个偏置项不重要，但是 Google 也有自己的理由和考虑，我觉得求同存异，看个人的理解吧。下面以一组例子说明这个公式的用法：

假设训练后的权重或者激活值的分布范围是[-3.0, 7.0]，INT8 量化后表示的范围[-128，127]，S 和 Z 可以计算如下：

S=7.0−(−3.0)127−(−128)=10255≈0.039216

Z=127−7.00.039216≈−51.498572≈−51

假设我们有一个激活值 0.78，即 R=0.78，则对应定点值求解如下：

Q=0.780.039216+(−51)≈−31.11016≈−31

可以看出，只要确定了浮点数的边界（定点数的边界时已知的），计算量化参数以及量化浮点数这些都和 TensorRT 以及 NCNN 非常的像，只不过 IAO 没有使用 KLD 那种方式寻找最佳阈值，而是直接使用要量化的数值集合的浮点数边界，和 NCNN 中 weights 的量化类似。

IAO 量化计算

和 TensorRT，我们根据量化公式也可以直接表示矩阵相乘：

S3(q3(i,k)−Z3)=∑j=1NS1(q1(i,j)−Z1)S2(q2(j,k)−Z2)

q3(i,k)=Z3+M∑j=1N(q1(i,j)−Z1)(q2(j,k)−Z2)

其中 M=S1S2S3，可以看到，整个式子中只有 M 是浮点数，其余都是整型（INT8 或者 INT32）。实验经验表明 M 的范围是 (0, 1)，因此想办法将其也用整数表示，做法如下：

M0=2nM

M0 是一个 (0.5, 1] 的数，记录 M 到 M0 的扩大（缩小）幅度 n（在计算机中可以用右移位数表示），然后将 M0 乘以 231，截断，得到一个 INT32 整形数 Mq。这里还有一个特别处理，如果 M0 接近 1，上述乘积结果 Mq 等于 231，超过 INT32 表示的最大值（231-1），因此将结果除以 2，相应的将记录的倍数 n 也减小 1。这样我们就可以用一个 INT32 整型数 Mq 和一个变化因子 n 来表示浮点数 M，从 Mq 恢复 M 就是上述过程的逆向操作。

IAO 量化训练

IAO 方法将权重、激活值及输入值均全部做 INT8 量化，并且将所有模型运算操作置于 INT8 下进行执行，以达到最好的量化效果。为了达到此目的，需要实施量化精度补偿训练。下面还是以一个卷积层计算的具体例子说明 IAO 量化训练：

输入量化的特征图 lhs_quantized_val，INT8 类型，偏移量 lhs_zero_point，INT32 类型；
输入量化的卷积核 rhs_quantized_val，INT8 类型，偏移量 rhs_zero_point，INT32 类型；
转换 INT8 到 INT32 类型；
每一块卷积求和（INT32 乘法求和有溢出风险，可换成固定点小数树乘法）；
- int32_accumulator += (lhs_quantized_val(i, j) - lhs_zero_point) * (rhs_quantized_val(j, k) - rhs_zero_point)
输入量化的乘子 quantized_multiplier（Mq，INT32 类型）和右移次数记录 right_shift（n)，INT 类型；
- real_multiplier = (S_in * S_W / S_out) * (2^n)
- quantized_multiplier = round(real_multiplier * (1 << 31))
计算乘法，得到 INT32 类型的结果 (INT32 乘法有溢出风险，可换成固定点小数树乘法);
- int32_result = quantized_multiplier * int32_accumulator
再左移动 right_shift 位还原，得到 INT32 的结果；
最后再加上结果的偏移量 result_zero_point；
将 INT32 类型结果强制转换到 INT8 类型，就得到了量化后的矩阵计算结果；
之后再反量化到浮点数，更新统计输出值分布信息 Rmax, Rmin；
再量化回 INT8；
之后经过量化激活层；
最后反量化到浮点数，本层网络输出；
进入下一层，循环执行 1~12 步骤

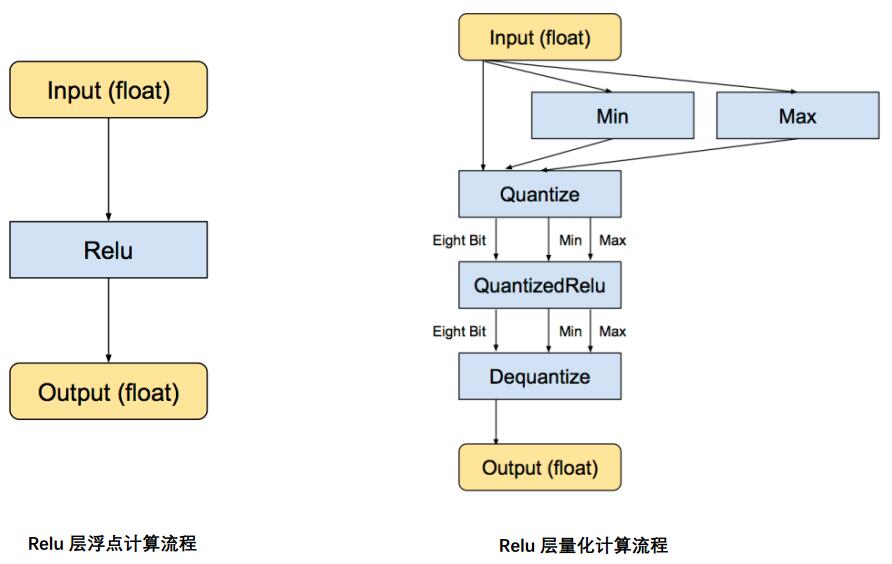
可以看出，上述的操作就是在传统神经网络的前向传播过程中加入量化和反量化的操作，这其中无疑引入了量化带来的精度误差，我个人理解量化训练的目的就是为了让参数分布适应这种误差。Relu 层的流程可以表示如下：

量化精度补偿训练需要一个具有代表性的小数据集，用于统计激活值和输入值等非确定性值的浮点型范围，以便进行精准量化，而输出值的 scale 计算则更加有意思，在训练最开始的时候将输出的值看作量化好的 INT8 类型，然后通过训练，不同搜集值得范围、计算 scale、调整，最后收敛。总体而言，其思想是和 TensorRT 中的校准数据集类似，只不过 IAO 方法直接收集的数值集合的最大最小值。全整型量化的输入输出依然是浮点型的，但如果某些 Op 未实现该方法，则转化是没问题的且其依然会自动保存为浮点型。

虽然是直接收集，但是针对卷积层和全连接层以及激活层的处理方式还是不同的。卷积层和全连接层处理方式类似都是直接统计最大值最小值，而激活层的值变化较大，因此使用一种称为 EMA 的方法来统计最大最小值。量化精度补偿训练一般是浮点模型训练的比较好的时候再进行，并且模拟量化的时候，反向传播仍然使用 FP32 类型，这是为了保证反向传播的精度。

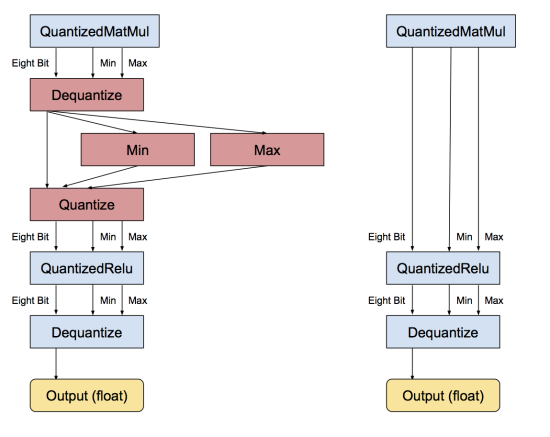
TensorFlow 中使用 IAO 方法也将卷积和结果和偏置项相加，激活层等操作进行了融合，还有一些实现细节，包括 BN 的更新等我就不展开叙述了。融合的计算流程如下：

总结

最后想说说量化适合的应用场景，由于量化是牺牲了部分精度（虽然比较小）来压缩和加速网络，因此不适合精度非常敏感的任务。量化目前最适合的领域就是图像处理，因为图片的信息冗余是非常大的，比如相邻一块的像素几乎都一模一样，因此用量化处理一些图像任务，比如目标检测、分类等对于精度不是非常敏感的 CV 任务而言是很适合的。

需要说明的是，量化只是深度神经网络压缩和加速的一种方法，还有包括蒸馏、矩阵秩分解、网络剪枝等多种方法。但是量化是一种已经获得了工业界认可和使用的方法，在训练（training）中使用 FP32，在推理（inference）期间使用 INT8 这套量化体系已经被包括 TensorRT，TensorFlow，PyTorch，MxNet 等众多深度学习框架启用。

就这两套方案而言，TensorRT 更加简单，实现起来也比较方便，IAO 方法在理论上精度更高，但是实际我自身只使用过前者，并没有验证过。后者如果使用 TensorFlow 的接口，使用也不难。

神经网络量化方法