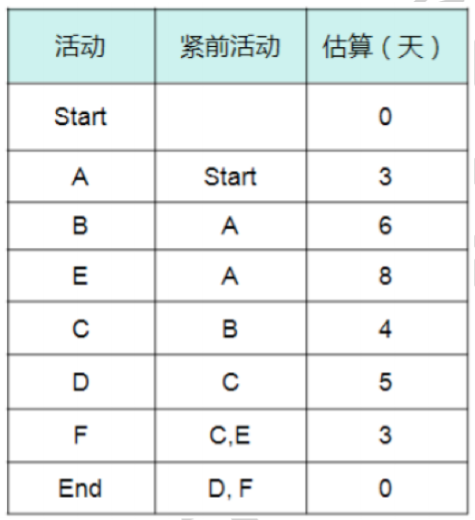
image.png
    根据这张图给出的活动之间逻辑关系，画出网络图。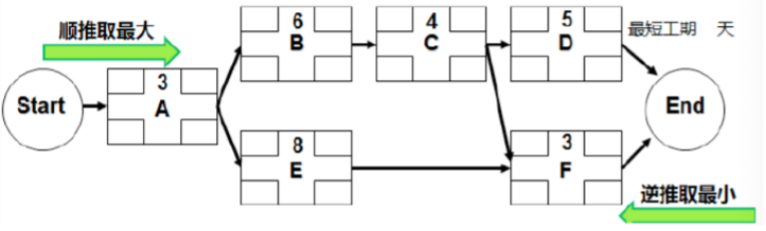
    image.png
    1）问项目最短工期？
    2）关键路径是哪条？
    3）活动 E 的（总）时差与自由时差？
    解题：
    1）关键路径决定着可能的项目最短工期。是最长的那条 A B C D，3+6+4+5=18 天 A E F，3+8+3=14 天 A B C F，3+6+4+3=16 天 因此，最短工期 18 天。
    2）关键路径 A B C D
    3）我们从 0 开始计算，所以 A 最早开始就是 0。
    关键路径上的活动时差为 0，所以 ABCD 的最早开始、最早结束、最晚开始、最晚结束， 都能确定。E 的最早开始、最早结束可以确定。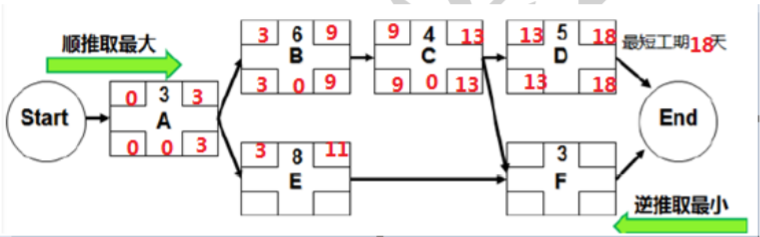
    image.png
    顺推取最大：顺推是针对 F 这个路径汇聚点而言，顺推是推 F 的最早开始，取了 CE 中 13、 11 中最大的 13，所以 F 最早开始就是 13。这句话就叫做“顺推取最大”。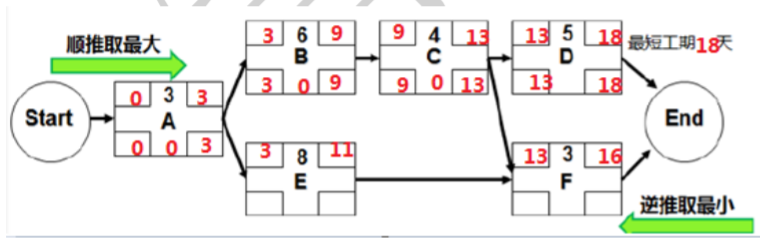
    image.png
    接着逆推，知道了工期为 18 天，所以 F 最晚可以在第 18 天完成，因此 F 的最晚结束时间为 18 天，推算 F 的最晚开始为 15 天。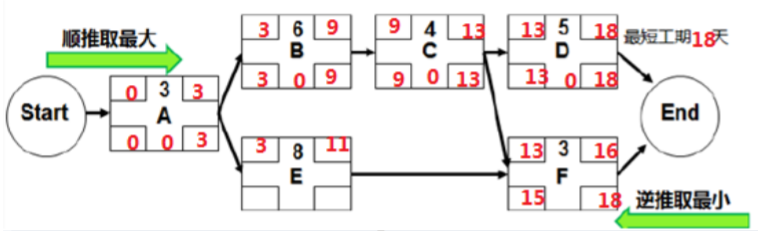
    image.png
    逆推取最小：逆推看最晚时间，针对 C 这个路径分支点，取了 DF 中 13、15 中最小的 13， 所以 C 最晚结束就是 13.当然 C 正好也是在关键路径上，我们之前通过判断关键路径也能 确定下来的。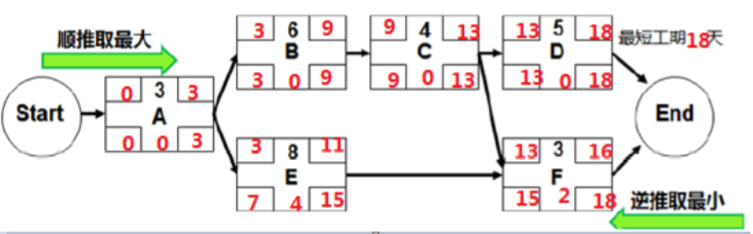
    image.png
    3）E 的总时差与自由时差
    E 的总时差=15-11，或 7-3=4 天。
    接着计算 E 的自由时差：自由时差的概念：不影响后续活动最早开始时间的前提下， 活动可以被推迟开始的时间。F 最早开始时间 13，所以 E 要在 13 天结束，13-11=2 天。
    E 的自由时差=2 天。

    关键路径法总结：
    PERT 是三点估算。关键路径法是单点估算，最可能的值来估算活动时间。不考虑任何 资源限制，找出路径最长的来确定最短工期，由于不考虑资源限制所以它是理论值。
    1）关键路径至少有一条；关键路径越多，风险越大；
    2）关键路径上的活动时差大多数情况等于 0，但也可以是正值或负值；
    3）如果关键活动的时差小于 0，表示关键活动延期了，或者管理层要求提前完工，这 时就需要进行进度压缩。