贝塔分布

三点估算结合正态分布图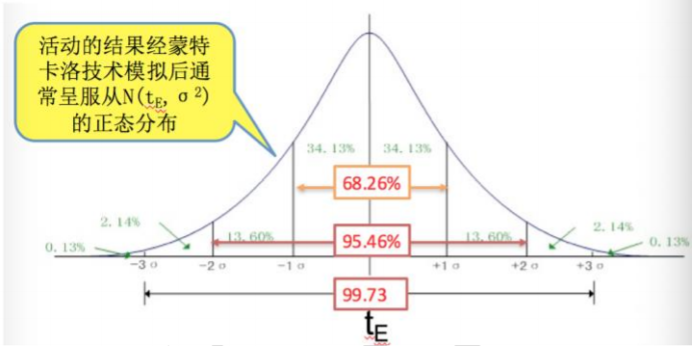

• 68.26%的结果数据位于均值的正负 1 西格玛内；
• 95.46%的结果数据位于均值的正负 2 西格玛内；
• 99.73%的结果数据位于均值的正负 3 西格玛内。

例：某活动的工期最乐观估算 6 天，最悲观估算 30 天，最可能估算为 9 天，那么：
1）8 至 16 天内完成该活动的概率的是多少？
A.68.26%
B.95.46%
C.99.73%
D.97.73%
解答：
均值=（6+4*9+30）/6=12 天；标准差/西格玛（30-6）/6=4 天；
正负 1 西格玛，8 天~16 天，这个区间完成活动的概率是 68.26%
正负 2 西格玛，4 天~20 天，这个区间完成活动的概率是 95.46%
正负 3 西格玛，0 天~24 天，这个区间完成活动的概率是 99.73%
这道题的问题 8 至 16 天完成，正好落在正负 1 西格玛的区间，答案 A。

2)在 20 天内完成该活动的概率是多少？
A.68.26%
B.95.46%
C.99.73%
D.97.73%
解答：

20 天，在正的 2 西格玛位置上，20 天内概率，是指负无穷～20 天这个区间的概率，也就是 负无穷到 2 西格玛区间，正态分布抛物线下面的面积，整个抛物线下面的面积是 1。
分两段计算：
第一段：负无穷～12 天，概率 50%，因为整个概率是 100%
第二段：12 天～20 天，是±2 个西格玛概率的一半，这个概率是 95.46%的一半 50%+95.46%/2=97.73%，
答案 D。

做这种题的思路是这样的：
1）、先计算均值和标准差；
2）、看题目要求计算的区间落在哪里，和三个给定的标准差的区间进行对比；
3）、其实计算区间概率，就是求抛物线下面区间的面积，整个抛物线下面的面积是 1。