1.概述
2 原理
- 2.1 样本分流
  - 谷歌分层实验框架论文
2.2 提升的衡量
3 实战经验
4 常见问题
- 4.1 辛普森悖论
- 4.2 A/B测试方法的副作用和处理办法
  - 多臂赌博机的定义
附录
- 附录A 流程
- 附录B 问题排查

1.概述

1.1 为什么AB实验平台必不可少？

1.1.1

1.1.2 1.1.3 市面上可参考的平台

美团AB平台-Gemi：《美团机器学习实践》第17章
云测AB实验：https://testin.cn/（内测版本已关闭）
贝壳流量实验平台-Athena：https://www.jianshu.com/p/79d31a72978f
腾讯实验平台：https://abtest.qq.com/
京东商户实验平台：http://aiceshi.shop.jd.com

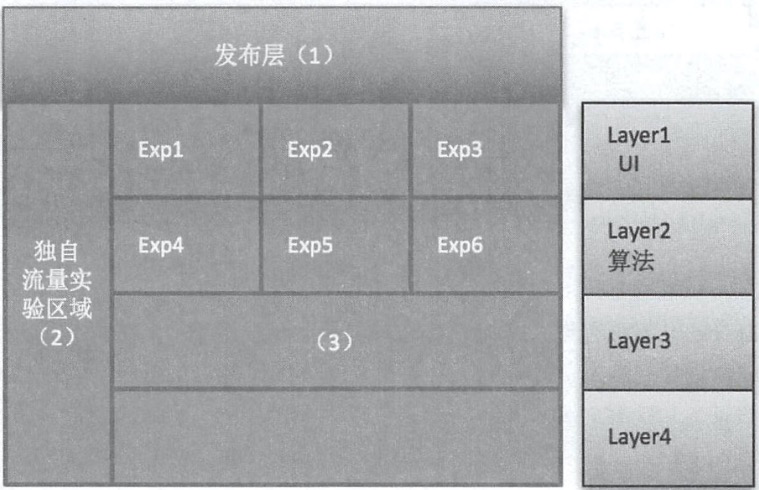
1.2 平台架构

1.2.1 架构设计图

1.2.2 使用接口定义

请求数据

-- 按单一AB实验访问
{
    "page": 1,
    "uid": "111122233"
}
-- 按一系列AB实验访问
{
    "biz": "test",
    "uid": "111122233"
}

返回数据

{
    "code": 0,
    "expid": [1, 2, 6],
    "params": {
        "add_recall": "deepfm",
        "use_rank": "dnn"
    }
}

1.3 AB平台的3大特性

AB平台要发挥数据驱动的作用，要做到三大特性：并行性、先验性、科学性。

1.3.1 并行性：实验正交进行

基准点

正交性：各层之间互相不影响
均匀性：实验组和对照组的流量是对等的
充足性：每个分支实验的流量是足够的
- 日均人数少于1000的实验结果波动将会非常大
- 日均人数大于2W的实验结果更具参考性
  最终目标
快速构建实验
随时上下线实验
同时支持多组实验

实现原理

**前提：在流量无穷的情况，每个层A组和B组的流量是均匀的

重点关注

实验流量分配
排除实验自身干扰

1.3.2 先验性：验证决策过程而非决策本身
A/B测试是当面对一个改进目标有两种甚至多种不同的方案的时候，为了避免盲目决策带来的不确定性好随机性，将各种不同的实验同时放到线上让实际目标群体选择，然后利用实际数据分析的结果来辅助进行决策的一种方式和手段。

所以A/B的常见的应用场景应该满足一下4个条件：

优化场景
- A/B测试并不能给出解决方案，而只是辅助我们对若干候选方案进行选择。
量化指标
- 要运用A/B测试来改进系统，另外一个重要的因素就是要改进的目标需要有一个或多个可量化的明确指标，并且这个指标会直接或间接收到该方案的影响
用户稳定
- 由于A/B测试将不同的设计或者策略呈现给一些随机的用户群体，之后统计各用户群体的群体指标，因此用户群体的选择和划分也是A/B测试是否成功的重要因素。
长期反馈
- 在设计和实现A/B测出实验的时候，要尽量控制除实验之外的影响因素保持固定
  建议流程
步骤一：提出目标
步骤二：建立假设
步骤三：设计方案
步骤四：执行实验
步骤五：分析数据
步骤六：发布版本

案例讲解

搜索是发现好物的开始，是电商平台主要的流量入口，可以说三分天下有其一

案例背景

搜索使用日均人次：3045w+（曝光）
搜索推荐词的日均CTR：0.38%

怎样提高搜索推荐词的CTR，节省用户时间？

步骤一：提出目标

提升CTR：节省更多用户更多时间，提升平台体验

步骤二：建立假设

CTR的原因（假设）

前端体验不佳
- 对搜索词进行标签分类
- 通过色彩突出搜索词
- 搜索词添加热度提示
后端推荐策略不佳
- 发掘用户偏好
- 匹配用户历史搜索
- 协同过滤算法
  步骤三：设计方案
A001：推荐词添加类别标签，如书籍/店铺/话题
A002：推荐词依据排列的位置，字体颜色渐变
A003：推荐词前三添加热度指数，体现词热度

步骤四：执行实验
抽样人群：20000人，权衡实验效果和成本
均匀分配：A001、A002、A003 三组均匀流量保证人群特征相似
上线环境：同时上线
监控数据：一致的统计方式，评估标准

步骤五：分析数据
数据短期看比较，长期看趋势，要经过一段的检验
总体的提升置信度提示等等
步骤六：发布版本
基于5的数据分析，选择A001是毫无争议的

1.3.3 科学性：经典的统计学理论

决策相关的统计学参考，详见2.2节。

2 原理

2.1 样本分流

谷歌分层实验框架论文

重叠实验框架.pdf

2.2 提升的衡量

（p-value , 置信区间，power的具体含义和计算方法）

2.2.1 基础概念

互逆假设

统计学上有2个互逆的假设：

原假设：我们希望通过试验结果推翻的假设
备择假设：我们希望通过试验结果验证的假设

在A/B测试过程中，我们试验的目的是通过反证法证明测试版本和对照版本有明显的不同（提升），因此在这个场景中，原假设就是原始版本和试验版本无差异，而备择假设就是这两个版本存在差异，因此，A/B试验的目的，做A/B试验的目的就是推翻2个版本无差异的原假设，验证他们有差异的备择假设。
**
在统计学上，存在两大错误，一是弃真错误，二是纳伪错误。

第一类错误(弃真错误）：原假设为真时拒绝了原假设

首先我们容易犯的就是第一类错误，就是原假设为真时拒绝了原假设，说白了就是过来就是2个版本无差异时候，我们错误的认为他们有差异（从统计学角度讲也叫弃真错误）这个错误的后果非常严重，所以我们把这它的标准设一个值0.05，它其实就是一个概率，这个概率就是我们容许自己出错的概率。
这个5%就是在统计学里的 α , 它代表着我们这个试验结果的置信水平。与这个置信水平相对应的就是置信区间的置信度，由 1- α 得出，所以你在这里看到如果 α 是0.05，那置信度就是0.95，也就是说，如果我们容许自己出错的几率是5%，那我们将得到一个有 95% 的可能性包含真实的总体均值区间范围，如果你把这个 α 调整成0.07，那你的置信区间的置信度将变成93%。
由于 α 是我们自己设置的，那么当然需要通过数据去验证一下，这个通过计算出来的值就是p-value ， p 的定义就是，如果两个版本无差异的前提下，得到当前试验数据的概率。
**

第二类错误（纳伪错误）：原假设为假时接受了原假设

第二类错误是指原假设为假时接受了原假设，即当2个版本有差异时候，我们错误的认为他们没有差异，这个错误的概率在统计学角度也称为取伪错误，记为 β ，这个概率可以相对大一些，业界大约定俗成的一个标准就是10%和20%的概率。
和显著性水平一样，为了避免我们犯第二类错误，我们需要通核算 β 从而计算出另一个参数来给我们参考，就是统计功效，和核算置信区间的置信度类似，它是的思路是 1-β 来得出（统计功效 power = 1 – β ）
统计功效是指版本差异（效果）为某个指定值时，通过显著性检验能正确地把差异检验出来的概率。说白了就是，假设两个版本的确存在差异，我们能够正确拒绝原假设，获得统计显著性结果（95%置信区间中数据）的概率。
统计功效的核算涉及样本数量，方差， α 、以及最小变化度或者置信区间下限。
由此可见，只有我们把第一类错误控制在5%以内，第二类错误控制在10%-20%左右，我们才可以说得出具有参考价值的出的试验数据。换句话说，我们在做A/B测试时，试验结果达到95%的置信度，以及80%-90%的统计功效时，它对我们来说才是有意义、可以作为决策参考的。
**

各值推理及计算

因为AB的统计符合二项分布，接下来的公式用二项分布做推导

p-value

p-value的定义是，如果两个版本无差异的前提下，得到当前试验数据的概率，其计算公式如下图所示，在A/B实验中，采用右侧检验的方式

中心极限定理说明，在适当的条件下，大量相互独立随机变量的均值经适当标准化后依分布收敛于正态分布（具体推导参考大数定理、中心极限定理），在样本数量比较大情况下，可以采用z检验。
ABtest需要采用双样本对照的z检验公式。

其中p代表转化率， 04 AB实验平台 - 图4 代表标准误差，由于转化过程是符合二项分布的，因此用户行为可以看作单次伯努利试验（single Bernoulli trial），而积极结果（完成转化）的可能性是未知的。假设样本数量足够大，我们可以使用广泛采用的Wald方法，将该分布近似为正态分布。因此有
04 AB实验平台 - 图5
04 AB实验平台 - 图6
04 AB实验平台 - 图7

根据计算出的z值，即可根据概率累积函数(CDF)计算出p-value
p-value = 1 - Φ(z)

置信区间

根据统计学的中心极限定理，样本均值的抽样分布呈正态分布。由之前计算得出Z值，再根据两个总体的均值、标准差和样本大小，利用以下公式即可求出两个总体均值差的置信度为α置信区间。

04 AB实验平台 - 图8
04 AB实验平台 - 图9

统计功效

统计功效是指版本差异（效果）为某个指定值时，通过显著性检验能正确地把差异检验出来的概率。说白了就是，假设两个版本的确存在差异，我们能够正确拒绝原假设，获得统计显著性结果（95%置信区间中数据）的概率。其计算公式如下图所示

2.2.2 代码实现

Java版本

import org.apache.commons.math3.distribution.NormalDistribution;
import java.math.BigDecimal;
import java.math.MathContext;
import java.math.RoundingMode;
import java.util.ArrayList;
import java.util.List;
/**
 * 描述:
 *
 * @author zhourao
 * @create 2020-04-26 2:40 下午
 */
public class AlalysisUtils {
    private static NormalDistribution nd = new NormalDistribution();
    private final static int SCALE = 16;
    //采用双边检测
    private static final double FIRST_TYPE_ERROR_CHANCE = 0.05;
    // 统计功效计算
    public static double GetStatisticalPower(BigDecimal expCt, BigDecimal controlCt, BigDecimal expCnt, BigDecimal controlCnt) {
        if (BigDecimal.ZERO.equals(expCt) && BigDecimal.ZERO.equals(controlCt)) {
            return 0;
        }
        BigDecimal zScore = GetZScore(expCt, controlCt, expCnt, controlCnt);
        BigDecimal staticZScore = BigDecimal.ZERO.subtract(new BigDecimal(nd.inverseCumulativeProbability(1 - FIRST_TYPE_ERROR_CHANCE / 2)));
        return 2 - nd.cumulativeProbability(staticZScore.add(zScore).doubleValue()) - nd.cumulativeProbability(staticZScore.subtract(zScore).doubleValue());
    }
    // 置信区间计算
    public static List<BigDecimal> GetConfidenceInterval(BigDecimal expCt, BigDecimal controlCt, BigDecimal expCnt, BigDecimal controlCnt) {
        List<BigDecimal> result = new ArrayList<>();
        if (BigDecimal.ZERO.equals(expCt) && BigDecimal.ZERO.equals(controlCt)) {
            result.add(BigDecimal.ZERO);
            result.add(BigDecimal.ZERO);
            return result;
        }
        BigDecimal expRatio = expCt.divide(expCnt, SCALE, BigDecimal.ROUND_HALF_UP);
        BigDecimal controlRatio = controlCt.divide(controlCnt, SCALE, BigDecimal.ROUND_HALF_UP);
        BigDecimal variance = getVariance(expRatio, controlRatio, expCnt, controlCnt);
        double v = nd.inverseCumulativeProbability(FIRST_TYPE_ERROR_CHANCE / 2);
        BigDecimal wave = variance.multiply(new BigDecimal(v)).abs();
        result.add(expRatio.subtract(controlRatio).subtract(wave));
        result.add(expRatio.subtract(controlRatio).add(wave));
        return result;
    }
    // p值计算
    public static double GetPValue(BigDecimal expCt, BigDecimal controlCt, BigDecimal expCnt, BigDecimal controlCnt) {
        if (BigDecimal.ZERO.equals(expCt) && BigDecimal.ZERO.equals(controlCt)) {
            return 1;
        }
        BigDecimal zScore = GetZScore(expCt, controlCt, expCnt, controlCnt);
        return 1 - nd.cumulativeProbability(zScore.doubleValue());
    }
    // z分数计算
    public static BigDecimal GetZScore(BigDecimal expCt, BigDecimal controlCt, BigDecimal expCnt, BigDecimal controlCnt) {
        BigDecimal expRatio = expCt.divide(expCnt, SCALE, BigDecimal.ROUND_HALF_UP);
        BigDecimal controlRatio = controlCt.divide(controlCnt, SCALE, BigDecimal.ROUND_HALF_UP);
        BigDecimal variance = getVariance(expRatio, controlRatio, expCnt, controlCnt);
        return (expRatio.subtract(controlRatio)).divide(variance, SCALE, BigDecimal.ROUND_HALF_UP).abs();
    }
    private static BigDecimal getVariance(BigDecimal expRatio, BigDecimal controlRatio, BigDecimal expCnt, BigDecimal controlCnt) {
        BigDecimal se_experiment = expRatio.multiply(BigDecimal.ONE.subtract(expRatio)).divide(expCnt, SCALE, BigDecimal.ROUND_HALF_UP);
        BigDecimal se_control = controlRatio.multiply(BigDecimal.ONE.subtract(controlRatio)).divide(controlCnt, SCALE, BigDecimal.ROUND_HALF_UP);
        return sqrt(se_experiment.add(se_control));
    }
    public static BigDecimal sqrt(BigDecimal value) {
        BigDecimal num2 = BigDecimal.valueOf(2);
        int precision = 100;
        MathContext mc = new MathContext(precision, RoundingMode.HALF_UP);
        BigDecimal deviation = value;
        int cnt = 0;
        while (cnt < precision) {
            deviation = (deviation.add(value.divide(deviation, mc))).divide(num2, mc);
            cnt++;
        }
        deviation = deviation.setScale(SCALE, BigDecimal.ROUND_HALF_UP);
        return deviation;
    }
}

2.2.3 使用流量建议

在做AB测试的时候，我们希望能测试两组间的转化率在统计上是否存在明显差异。由于样本量大，我们可以采用双样本单尾z-检验（two-sample, one-tailed z-test）。另外，对于较小的样本集合，我们可以依赖于t-检验。

转化率的数据分布按二项分布计算

大流量-z检验

大流量及推荐用户量

确定相较原来有转化率的增长，置信度95%（p-value<0.05）

序号	原始转化率	增长1%需要各组人数	增长2%需要各组人数
1	5%	1032974	259459
2	10%	489160	122829
3	20%	217253	54514
4	30%	126617	31743
5	40%	81299	20357
6	50%	54109	13526

过程推理

按二项分布，推导的z值求解公式如下：
04 AB实验平台 - 图11
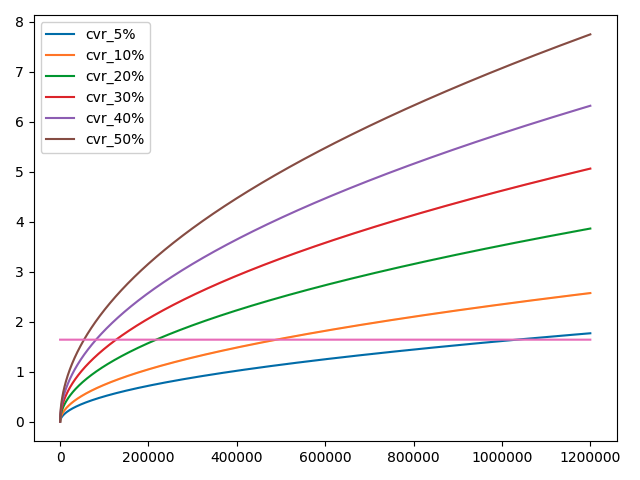
置信区间95%对应的z值为1.65，按相对原来增长1%计算

import math
import matplotlib.pyplot as plt
from scipy.stats import norm

def get_cnt(old_cvr, ratio):
    p_experiment = old_cvr + old_cvr * ratio
    p_control = old_cvr

    return (p_experiment * (1 - p_experiment) + p_control * (1 - p_control)) / math.pow(old_cvr * ratio / norm.ppf(0.95), 2)


# 按相对原来增长1%计算
def get_z(old_cvr, cnt, ratio):
    p_experiment = old_cvr + old_cvr * ratio
    p_control = old_cvr

    n_experiment = cnt
    n_control = cnt
    se_experiment = p_experiment * (1 - p_experiment) / n_experiment
    se_control = p_control * (1 - p_control) / n_control
    return (p_experiment - p_control) / math.sqrt(se_experiment + se_control)


print(get_cnt(0.05, 0.01))
print(get_cnt(0.10, 0.01))
print(get_cnt(0.20, 0.01))
print(get_cnt(0.30, 0.01))
print(get_cnt(0.40, 0.01))
print(get_cnt(0.50, 0.01))

print(get_cnt(0.05, 0.02))
print(get_cnt(0.10, 0.02))
print(get_cnt(0.20, 0.02))
print(get_cnt(0.30, 0.02))
print(get_cnt(0.40, 0.02))
print(get_cnt(0.50, 0.02))

x = range(1, 1200000, 100)
y_5 = []
y_10 = []
y_20 = []
y_30 = []
y_40 = []
y_50 = []
line_2 = []
for i in x:
    y_5.append(get_z(0.05, i, 0.01))
    y_10.append(get_z(0.10, i, 0.01))
    y_20.append(get_z(0.20, i, 0.01))
    y_30.append(get_z(0.30, i, 0.01))
    y_40.append(get_z(0.40, i, 0.01))
    y_50.append(get_z(0.50, i, 0.01))
    line_2.append(norm.ppf(0.95))  # 0.95

plt.plot(x, y_5, label='cvr_5%')
plt.plot(x, y_10, label='cvr_10%')
plt.plot(x, y_20, label='cvr_20%')
plt.plot(x, y_30, label='cvr_30%')
plt.plot(x, y_40, label='cvr_40%')
plt.plot(x, y_50, label='cvr_50%')
plt.plot(x, line_2)
plt.legend(['cvr_5%', 'cvr_10%', 'cvr_20%', 'cvr_30%', 'cvr_40%', 'cvr_50%'])
plt.show()

结果图

小流量-t检验

小用户流量推荐：单边检测，统计功效大于80%，

import math
from scipy.stats import norm


def get_cnt(old_cvr, ratio):
    p_experiment = old_cvr + old_cvr * ratio
    p_control = old_cvr

    return math.ceil(
        (norm.ppf(0.95) + norm.ppf(0.8)) ** 2 * (p_experiment * (1 - p_experiment) + p_control * (1 - p_control)) / (
                old_cvr * ratio ** 2))


print(get_cnt(0.05, 0.01))
print(get_cnt(0.10, 0.01))
print(get_cnt(0.20, 0.01))
print(get_cnt(0.30, 0.01))
print(get_cnt(0.40, 0.01))
print(get_cnt(0.50, 0.01))

print(get_cnt(0.05, 0.02))
print(get_cnt(0.10, 0.02))
print(get_cnt(0.20, 0.02))
print(get_cnt(0.30, 0.02))
print(get_cnt(0.40, 0.02))
print(get_cnt(0.50, 0.02))

序号	原始转化率	增长1%需要各组人数	增长2%需要各组人数
1	5%	118025	29646
2	10%	111781	28069
3	20%	99291	24915
4	30%	86802	21761
5	40%	74312	18608
6	50%	61823	15454

3 实战经验

3.1 指标体系的设立

3.3.1 常用指标类别

人次
频次
人均
- 普通人均=频次/人次
- 同一个人重复点击去除的人均，A点击了B 2次、C 1次，按上述人均是3，按此人均是2
频次转化率
人次转化率
总和（如成交金额）
3.2 结合数据分析
3.2.1 AAARR漏斗模型
3.2.2 渠道分析统计

3.3 报表统计分层

4 常见问题

4.1 辛普森悖论

4.2 A/B测试方法的副作用和处理办法

对于非常小的效果变化，往往都需要创建相当大的对照组和测试组来实现AB测试，这个的代价往往是很大的。设想下在零售商场中，每天观察到的用户数量，往往需要很久的时间才能得出明显的结论。在实际业务应用中，会遇到的问题是：当你运行测试时整体运行的效果是受到很大影响的，因为必须有一半的用户处于效果不佳的实验组，或者有一半的用户处于效果不佳的对照组，而且你必须等待测试完成才能停止这种局面。

这是被称为探索利用难题（explore-exploit conundrum）的一个经典问题。我们需要运行次优方法，以探索空间，并找到效果更好的解决方案，而一旦找到了更好的解决方案，我们还需要尽快利用它们来实现效果提升。能否可以更快地利用新的解决方案，而不必等待测试完全完成呢？答案是肯定的。下面简单介绍下多臂赌博机（multi-armed bandit，MAB）的概念。

多臂赌博机的定义

多臂赌博机（multi-armed bandit，MAB）的名字来源于著名的赌博游戏角子赌博机（one-armed bandit）。对那些从没去过赌场的人，我们来做下解释：角子机（又称老虎机）是一个需要你拉杠杆（或摇臂）的赌博机器，根据机器展示的数值，你可能会得到一笔奖励，也可能（更大几率）得不到任何东西。和你想的一样，这些机器的设置都对庄家有利，所以能获的奖励的几率是非常非常小的。

多臂赌博机（理论上的）扩展了这种形式，想象你面对的是一堆角子赌博机，每个赌博机都被分配按照一个独立的概率进行奖励。作为一个玩家，你不知道在这些机器后的获奖概率，你唯一可以找到获奖概率的方法是进行游戏。你的任务是通过玩这些机器，最大限度地提高所获的奖励。那么你应该使用什么策略呢？

04 AB实验平台