哈夫曼树和哈夫曼编码

• 哈夫曼树的构造
• 哈夫曼编码的构造

一、哈夫曼树的构造

首先给出树的几个概念：

• 路径：从树种一个结点到另一个结点之间的分支构成这两个结点之间的路径，路径上的分支数目称作路径长度。
• 树的路径长度：从树根到每一个结点的路径长度之和。
• 结点的带权路径长度：为从该结点到树根的之间的路径长度与结点上权的成绩。
• 树的带权路径长度：为数中所有叶子结点的带权路径长度之和。

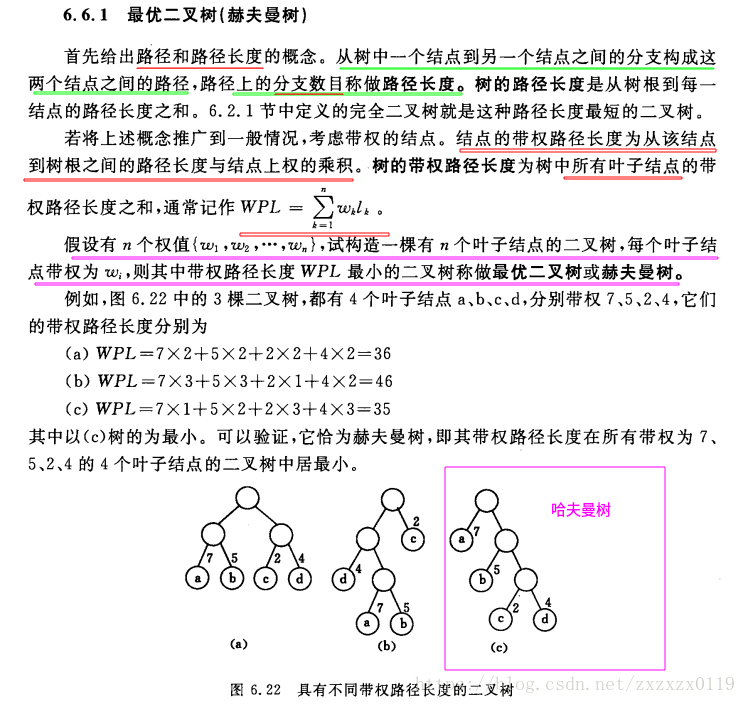
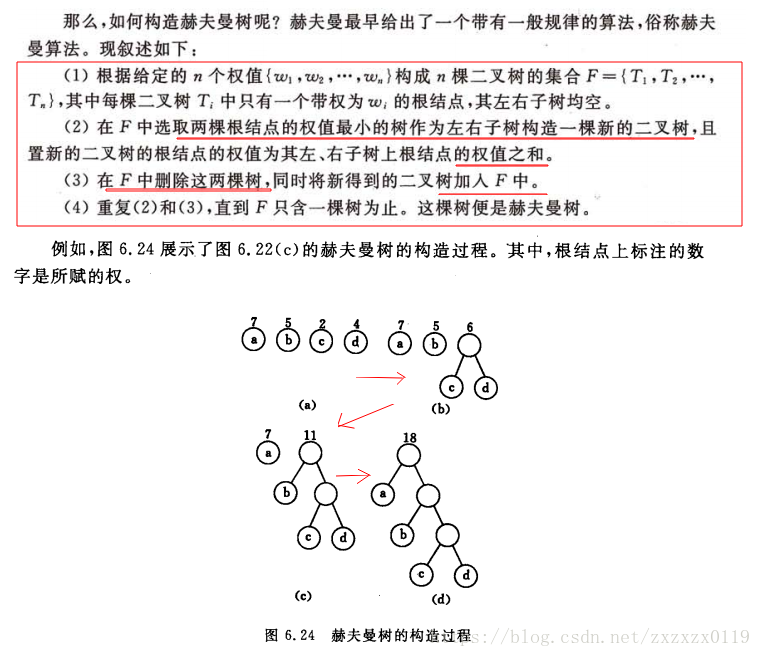
• 构建哈夫曼树的思想其实就是贪心的思想，每次在目前可选的树结点中，选取两个最小的结点，构造成一颗新的二叉树，直到只有一棵树为止。

二、哈夫曼编码的构造

那么如何构造出最优的前缀编码，也就是赫夫曼编码呢?

注意这里的huffCodes存储的哈夫曼编码的技巧:

• 首先我是从每一个叶子从下往上去构造哈夫曼编码；
• 然后我的数组也是从每一行的最后一个开始构造(idx = n - 1)；
• 也就是说每一个一维数组内，我是从最后开始存，存的是从叶子到根的，存完之后，加上一个-1，然后我输出的时候，从数组的前面开始，碰到-1，就说明编码的开始(也就是说译码其实是从根到叶子的过程，但是这里是从叶子到根构建的)；

看下图:

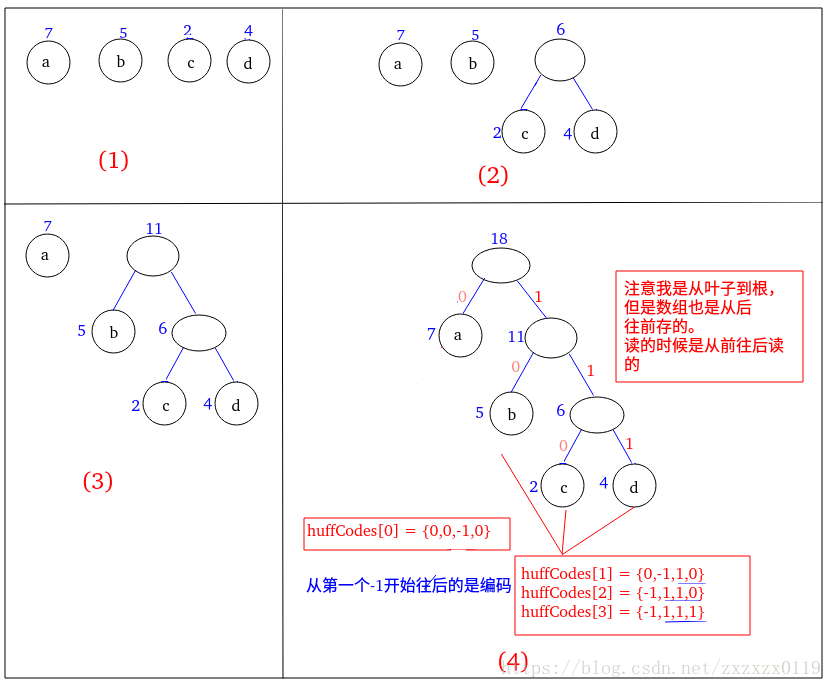
代码如下:

import java.util.LinkedList;
import java.util.Queue;
public class HuffmanTree {
    private static class Node {
        private int val;
        private boolean flag; //标记是否已经被选
        private Node parent; // 父亲结点
        private Node left;
        private Node right;
        public Node(int val) {
            this(val, false , null, null, null);
        }
        public Node(int val, boolean flag, Node parent, Node left, Node right) {
            super();
            this.val = val;
            this.flag = flag;
            this.parent = parent;
            this.left = left;
            this.right = right;
        }
    }
    //每次选出一个最小的结点的函数
    public static Node selectMin(Node[] HN,int end){ //找到最小的一个结点
        Node minNode = HN[end];
        for(int i = 0; i <= end; i++){
            if(HN[i].flag == false && HN[i].val < minNode.val){
                minNode = HN[i];
            }
        }
        return minNode;
    }
    //建立赫夫曼树
    public static Node[] build(int[] w){
        int m = w.length * 2 - 1;
        Node[] HN = new Node[m+1];
        for(int i = 0; i < w.length; i++) //先建立好前面的叶子结点
            HN[i] = new Node(w[i]);
        /**
         * 已经有w.length - 1个叶子结点，现在要建立 从w.length ~ (2*w.length-1) 的结点
         */
        for(int i = w.length; i < m; i++){
            Node firstNode = selectMin(HN, i-1); //从前面的结点中找到第一个最小的
            firstNode.flag = true;
            Node secondNode = selectMin(HN, i-1); //从前面的结点中找到第二个最小的
            secondNode.flag = true;
            HN[i] = new Node(firstNode.val + secondNode.val); //新结点的值是两个最小结点的和
            //设置好孩子和孩子的父亲
            HN[i].left = firstNode;
            HN[i].right = secondNode;
            firstNode.parent = HN[i];
            secondNode.parent = HN[i];
        }
        return HN; //返回结点数组
    }
    public static void leverOrder(Node root){
        if(root == null)
            return;
        Queue<Node> que = new LinkedList<Node>();
        que.add(root);
        while(!que.isEmpty()){
            Node cur = que.poll();
            System.out.print(cur.val + " ");
            if(cur.left != null)
                que.add(cur.left);
            if(cur.right != null)
                que.add(cur.right);
        }
        System.out.println();
    }
    //哈夫曼编码 :  从叶子到根的一个路径
    public static int[][] huffmanCoding(Node[] HN, int n){
        int[][] huffCodes = new int[n][n];
        for(int i = 0; i < n; i++){
            int idx = n-1;  //逆向存储
            for(Node cur = HN[i], pa = cur.parent ;  pa != null;  cur = pa,pa = pa.parent){
                if(pa.left == cur) //左孩子为0
                    huffCodes[i][idx--] = 0;
                else                    //右孩子为1
                    huffCodes[i][idx--] = 1;
            }
            huffCodes[i][idx--] = -1; //标记一下 从-1往后的是真的编码 前面的不足
        }
        return huffCodes;
    }
    public static void main(String[] args) {
        int[] w = {7,5,2,4};   //  给出叶子的权值数组
        Node[] HN = build(w);
        System.out.println("-----哈夫曼树-----");
        leverOrder(HN[2 * w.length - 2]); //最后的根 的下标
        int[][] huffCodes = huffmanCoding(HN,w.length); //开始从叶子到根构建编码
        System.out.println("----哈夫曼编码-----");
        for(int i = 0; i < w.length; i++){
            System.out.print(w[i] + ": ");
            for(int j = 0; j < huffCodes[i].length; j++){
                if(huffCodes[i][j] == -1){    //从-1标记的开始往后的才是编码
                    for(int k = j + 1; k < huffCodes[i].length; k++)
                        System.out.print(huffCodes[i][k]);
                    break;
                }
            }
            System.out.println();
        }
    }
}

运行效果:

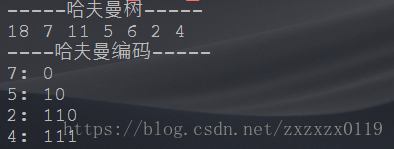
对照上面的例子，可以看出来是对的。

另一种写法: 使用ArrayList存储哈夫曼编码:

import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;
public class HuffmanTree2 {
    private static class Node {
        private int val;
        private boolean flag; //标记是否已经被选
        private Node parent; // 父亲结点
        private Node left;
        private Node right;
        public Node(int val) {
            this(val, false , null, null, null);
        }
        public Node(int val, boolean flag, Node parent, Node left, Node right) {
            super();
            this.val = val;
            this.flag = flag;
            this.parent = parent;
            this.left = left;
            this.right = right;
        }
    }
    //每次选出一个最小的结点的函数
    public static Node selectMin(Node[] HN,int end){ //找到最小的一个结点
        Node minNode = HN[end];
        for(int i = 0; i <= end; i++){
            if(HN[i].flag == false && HN[i].val < minNode.val){
                minNode = HN[i];
            }
        }
        return minNode;
    }
    //建立赫夫曼树
    public static Node[] build(int[] w){
        int m = w.length * 2 - 1;
        Node[] HN = new Node[m+1];
        for(int i = 0; i < w.length; i++) //先建立好前面的叶子结点
            HN[i] = new Node(w[i]);
        /**
         * 已经有w.length - 1个叶子结点，现在要建立 从w.length ~ (2*w.length-1) 的结点
         */
        for(int i = w.length; i < m; i++){
            Node firstNode = selectMin(HN, i-1); //从前面的结点中找到第一个最小的
            firstNode.flag = true;
            Node secondNode = selectMin(HN, i-1); //从前面的结点中找到第二个最小的
            secondNode.flag = true;
            HN[i] = new Node(firstNode.val + secondNode.val); //新结点的值是两个最小结点的和
            //设置好孩子和孩子的父亲
            HN[i].left = firstNode;
            HN[i].right = secondNode;
            firstNode.parent = HN[i];
            secondNode.parent = HN[i];
        }
        return HN; //返回结点数组
    }
    public static void leverOrder(Node root){
        if(root == null)
            return;
        Queue<Node> que = new LinkedList<Node>();
        que.add(root);
        while(!que.isEmpty()){
            Node cur = que.poll();
            System.out.print(cur.val + " ");
            if(cur.left != null)
                que.add(cur.left);
            if(cur.right != null)
                que.add(cur.right);
        }
        System.out.println();
    }
    //哈夫曼编码 :  从叶子到根的一个路径
    public static ArrayList[] huffmanCoding(Node[] HN, int n){
        ArrayList[] huffCodes = new ArrayList[n];
        for(int i = 0; i < huffCodes.length; i++)
            huffCodes[i] = new ArrayList<Integer>();
        for(int i = 0; i < n; i++){
            for(Node cur = HN[i], pa = cur.parent ;  pa != null;  cur = pa,pa = pa.parent){
                if(pa.left == cur) //左孩子为0
                    huffCodes[i].add(0);
                else                    //右孩子为1
                    huffCodes[i].add(1);
            }
        }
        return huffCodes;
    }
    public static void main(String[] args) {
        int[] w = {7,5,2,4};   //  给出叶子的权值数组
        Node[] HN = build(w);
        System.out.println("-----哈夫曼树-----");
        leverOrder(HN[2 * w.length - 2]); //最后的根 的下标
        ArrayList[] huffCodes = huffmanCoding(HN,w.length); //开始从叶子到根构建编码
        System.out.println("----哈夫曼编码-----");
        for(int i = 0; i < w.length; i++){
            System.out.print(w[i] + ": ");
            for(int j = huffCodes[i].size() - 1; j >= 0; j--)
                System.out.print(huffCodes[i].get(j));
            System.out.println();
        }
    }
}