二叉树的各种操作(递归和非递归遍历,树深度,结点个数等等)

二叉树建立

先给出结点结构:

  1. static class Node {
  2.     public int val;
  3.     public Node left;
  4.     public Node right;
  6.     public Node(int val) {
  7.         this.val = val;
  8.     }
  9. }

两种建立方式:

  • 可以根据二叉树根节点和左右子结点的下标关系递归建立二叉树，层次输入二叉树结点；
  • 也可以使用输入流前序建立二叉树(注意空树要输入-1)；

1、根据下标关系

  1. // given a arr to build
  2. static Node createTree(int arr[], int i) {
  3.     if (i >= arr.length || arr[i] == -1)
  4.         return null;
  5.     Node root = new Node(arr[i]);
  6.     root.left = createTree(arr, 2 * i + 1);
  7.     root.right = createTree(arr, 2 * i + 2);
  8.     return root;
  9. }

大致过程如下:
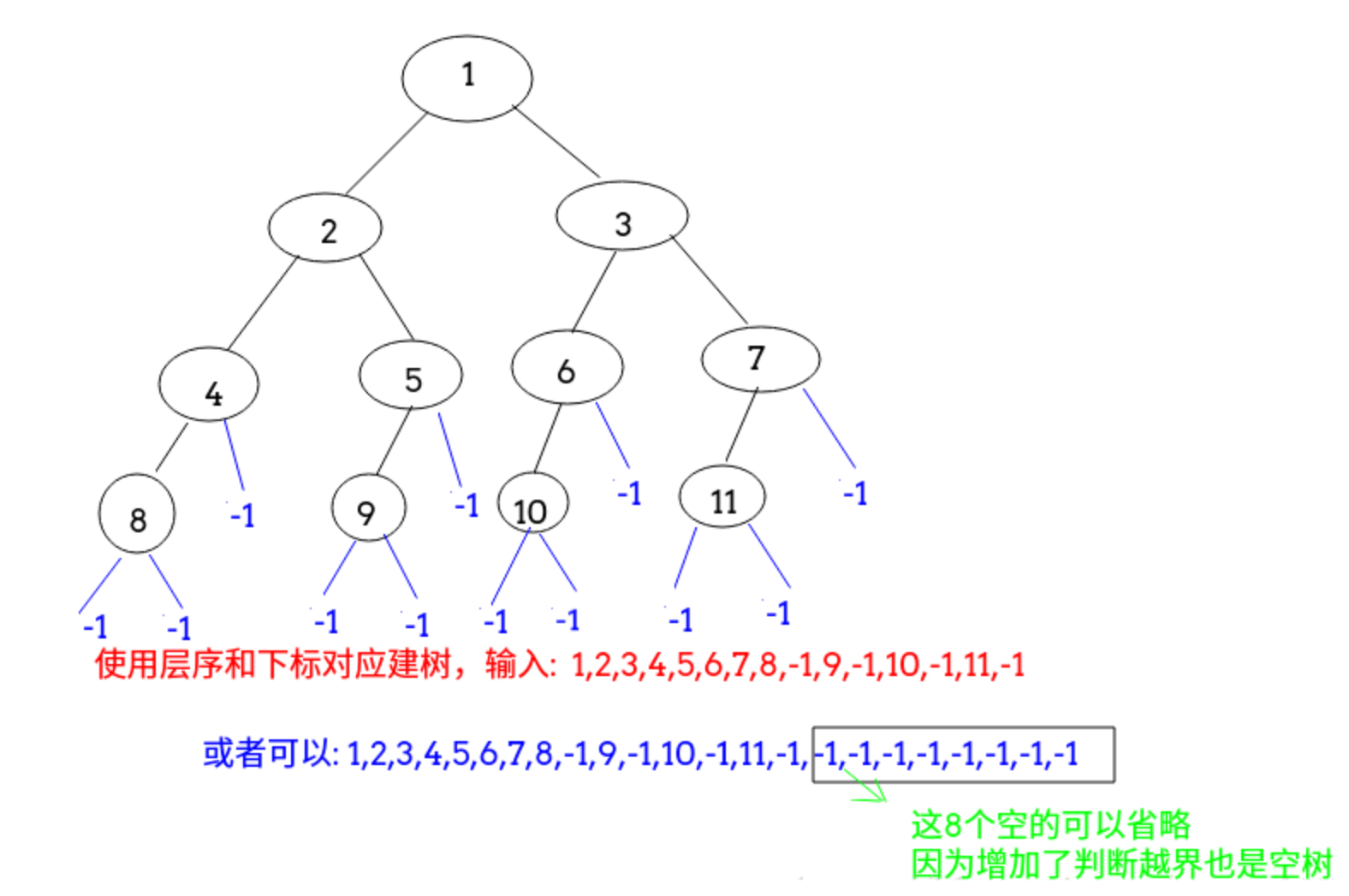
image.png

2、前序输入(cin)建立

  1. // cin method    
  2. static Node buildTree(Scanner cin) {
  3.     Node root = null;
  4.     int data = cin.nextInt();
  5.     if (data != -1) {
  6.         root = new Node(data);
  7.         root.left = buildTree(cin);
  8.         root.right = buildTree(cin);
  9.     }
  10.     return root;
  11. }

过程如下:
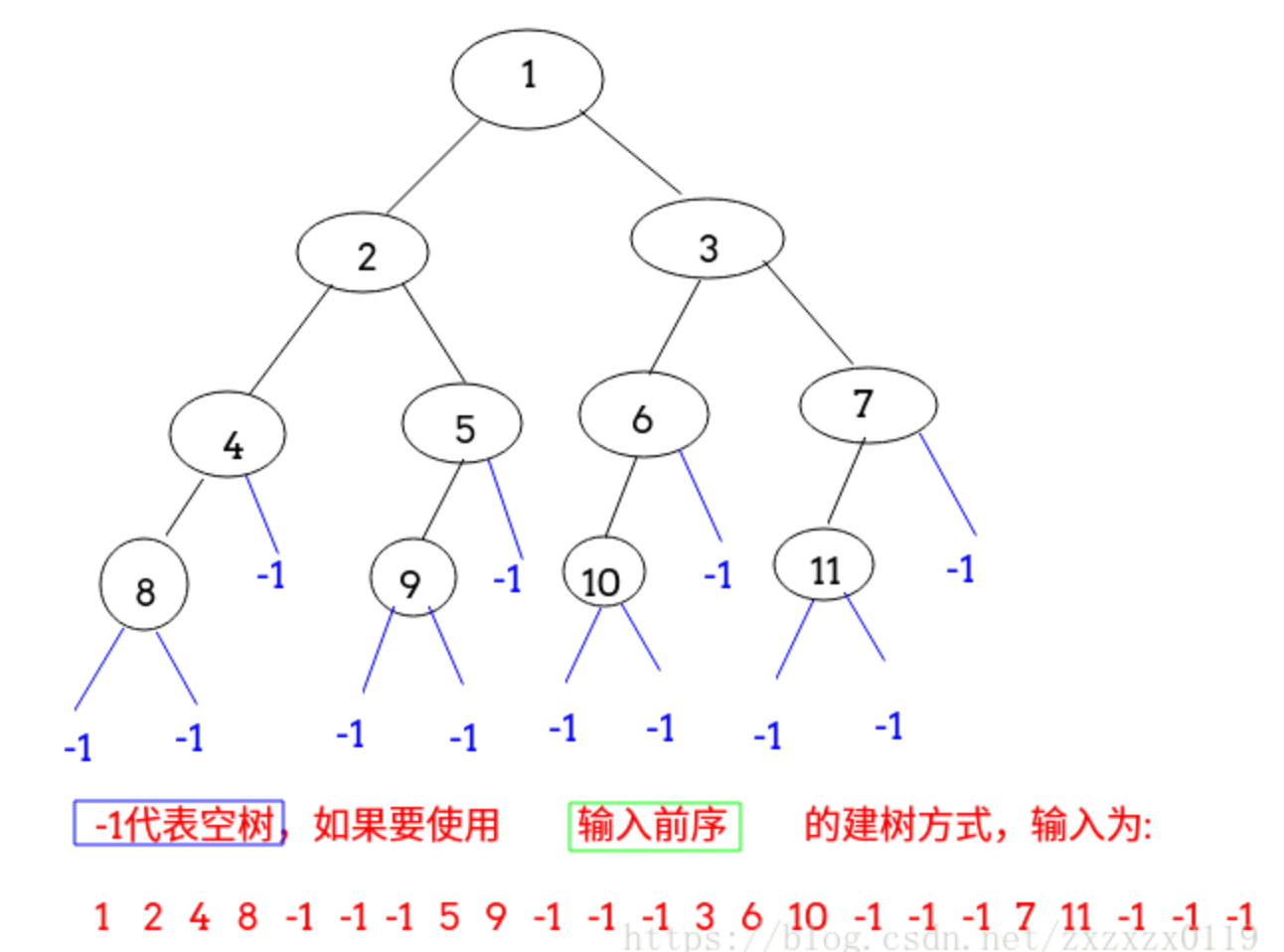
image.png

前序遍历

1、递归前序

  1. static void preOrder(Node T) {
  2.     if (T == null)
  3.         return;
  4.     System.out.print(T.val + " ");
  5.     preOrder(T.left);
  6.     preOrder(T.right);
  7. }

2、非递归前序

前序遍历顺序为: 根结点->左子树->右子树，所以对于正在访问的根结点，可以直接访问，访问完之后，按照相同的方式访问左子树，再访问右子树，过程如下 :

  • 如果当前节点p不为空，访问结点p，并将结点p入栈，并继续访问左子树(直到左子树为空)；
  • 否则将栈顶元素出栈，并访问栈顶的元素的右子树；
  • 直到栈为空且p为空，循环结束。

代码:

  1. static void iterativePre(Node root) {
  2.     Stack<Node> s = new Stack<>();
  3.     Node p = root;
  4.     while (!s.empty() || p != null) {
  5.         if (p != null) {//也可以写一个while循环，直到左子树为空
  6.             s.push(p);
  7.             System.out.print(p.val + " ");
  8.             p = p.left;
  9.         } else {
  10.             p = s.pop();
  11.             p = p.right;
  12.         }
  13.     }
  14. }

也可以将上面的一直访问到左子树为空写成一个while循环:

  1. static void iterativePre2(Node root) {
  2.     Stack<Node> s = new Stack<>();
  3.     Node p = root;
  4.     while (!s.empty() || p != null) {
  5.         while (p != null) { // while循环，直到左子树为空
  6.             s.push(p);
  7.             System.out.print(p.val + " ");
  8.             p = p.left;
  9.         }
  10.         p = s.pop();
  11.         p = p.right;
  12.     }
  13. }

还有另外一种写法是:

  • 先把根节点入栈，然后每次出栈一个元素，先访问这个元素，然后如果它的右子树存在，就入栈，如果它的左子树存在也入栈；
  • 为什么要先入右子树呢，因为，前序遍历是中->左->右，而栈可以逆序，所以先右再左；

这个方法在后续遍历的双栈法中有体现，那个只是这个稍微的修改。

  1. static void iterativePre3(Node root) {
  2.     if (root == null)
  3.         return;
  4.     Node p = root;
  5.     Stack<Node> stack = new Stack<>();
  6.     stack.add(p);
  7.     while (!stack.isEmpty()) {
  8.         p = stack.pop();
  9.         System.out.print(p.val + " ");
  10.         if (p.right != null)// 先右再左即可
  11.             stack.push(p.right);
  12.         if (p.left != null)
  13.             stack.push(p.left);
  14.     }
  15. }

中序遍历

1、递归中序

  1. static void inOrder(Node T) {
  2.     if (T == null)
  3.         return;
  4.     inOrder(T.left);
  5.     System.out.print(T.val + " ");
  6.     inOrder(T.right);
  7. }

2、非递归中序

中序遍历 : 左子树->根->右子树，过程如下：

  • 当前节点不空!= null，压入栈中(和前序遍历不同的是，不需要打印)，当前节点向左；
  • 当前节点为空== null，从栈中拿出一个并且打印(在这里打印) ，当前节点向右；

直到栈为空且p为空，循环结束。

  1. /**
  2. * 1)、当前节点不空(!=null)，压入栈中(和前序遍历不同的是，不需要打印)，当前节点向左；
  3. * 2)、当前节点为空(==null)，从栈中拿出一个并且打印(在这里打印) ，当前节点向右；
  4. */
  5. static void iterativeIn(Node root) {
  6.     if (root == null)
  7.         return;
  8.     Stack<Node> s = new Stack<>();
  9.     Node p = root;
  10.     while (!s.empty() || p != null) {
  11.         if (p != null) {
  12.             s.push(p);
  13.             p = p.left;
  14.         } else {
  15.             p = s.pop();
  16.             System.out.print(p.val + " "); //在这里打印
  17.             p = p.right;
  18.         }
  19.     }
  20. }

同理，那个一直访问左孩子那里也可以改成whlie:

  1. static void iterativeIn2(Node root) {
  2.     if (root == null)
  3.         return;
  4.     Stack<Node> s = new Stack<>();
  5.     Node p = root;
  6.     while (!s.empty() || p != null) {
  7.         while (p != null) { //这里改成while
  8.             s.push(p);
  9.             p = p.left;
  10.         }
  11.         p = s.pop();
  12.         System.out.print(p.val + " "); //在这里打印
  13.         p = p.right;
  14.     }
  15. }

后序遍历

1、递归后序

  1. static void postOrder(Node T) {
  2.     if (T == null)
  3.         return;
  4.     postOrder(T.left);
  5.     postOrder(T.right);
  6.     System.out.print(T.val + " ");
  7. }

2、非递归后序

1)、双栈法

这个其实就是非递归前序(iterativePre3)的稍微一点改进。

  • 首先，前序遍历入栈(iterativePre3)的顺序是先 右　再左；
  • 这时，我们可以做到反过来先　左　再右，这样遍历的顺序可以做到 “中右左”，而后续遍历是 “左右中”，正好是前面那个的相反，所以我们再使用一个栈反转保存即可；

代码:

  1. /**
  2. * 非递归后续1(双栈法解决非递归后续)
  3. * 后续遍历是要实现　　　左->右->中
  4. * 这个方法和前序遍历的第二种方法　只是多了一个栈而已
  5. * 因为　前序遍历是  中->左->右　　压栈顺序是 右->左
  6. * 这样，我们就很容易实现　中->右->左遍历　　压栈顺序是　左->右
  7. * 而后续遍历是要实现  左->右->中，
  8. * 我们把上面的　　中右左　压入到另一个栈中　就实现了　左右中
  9. */
  10. static void iterativePos(Node root) {
  11.     Stack<Node> s = new Stack<>(), s2 = new Stack<>();
  12.     Node p;
  13.     s.push(root);
  14.     while (!s.empty()) {
  15.         p = s.pop();
  16.         s2.push(p);
  17.         if (p.left != null) s.push(p.left); //这里是先左再右  (非递归前序是先右再左)
  18.         if (p.right != null) s.push(p.right);
  19.     }
  20.     while (!s2.empty())
  21.         System.out.print(s2.pop().val + " ");
  22. }

2)、设置pre结点

过程如下:

  • 对于任一结点p，先将其入栈；
  • 可以访问的情况: ①若p不存在左孩子和右孩子，则可以直接访问它。②或者p存在左孩子或者右孩子，但是左孩子和右孩子都已经被访问过了，则也可以直接访问该结点；
  • 若非上述两种情况，则将右孩子和左孩子依次入栈。这样可以保证每次取栈顶元素时，左孩子在右孩子前面被访问，根结点在左孩子和右孩子访问之后被访问；

代码:

  1. /*** 非递归后续2(设置pre结点) */
  2. static void iterativePos2(Node root) {
  3.     Node cur, pre = null;
  4.     Stack<Node> s = new Stack<>();
  5.     s.push(root);
  6.     while (!s.empty()) { 
  7.         cur = s.peek();
  8.         // 两种可以访问的情况
  9.         if ((cur.left == null && cur.right == null) ||
  10.             ((pre != null) && (pre == cur.left || pre == cur.right))) {
  11.             System.out.print(cur.val + " ");
  12.             s.pop();
  13.             pre = cur;
  14.         } else {
  15.             if (cur.right != null) s.push(cur.right);
  16.             if (cur.left != null) s.push(cur.left);
  17.         }
  18.     }
  19. }

层次遍历

很简单。利用队列BFS即可.

算法思想:

1.初始将根入队并访问根节点，然后出队

2.若有左子树，则将左子树入队

3.若有右子树，则将右子树入队

4.然后出队，访问该节点

5.反复该过程直到队列为空

  1. static void levelOrder(Node root) {
  2.     if (root == null)
  3.         return;
  4.     Queue<Node> queue = new LinkedList<>();
  5.     queue.add(root);
  6.     while (!queue.isEmpty()) {
  7.         Node now = queue.poll();
  8.         System.out.print(now.val + " ");
  9.         if (now.left != null) queue.add(now.left);
  10.         if (now.right != null) queue.add(now.right);
  11.     }
  12. }

寻找树中有没有值为x的结点

递归条件有两个，一个是为空代表没找到，找到了的话直接返回，否则递归查找左右子树。

  1. //查找某个值为x的结点
  2. static Node search(Node T, int x) {
  3.     if (T == null)
  4.         return null;
  5.     if (T.val == x)
  6.         return T;
  7.     else {
  8.         if (search(T.left, x) == null)
  9.             return search(T.right, x);
  10.         else
  11.             return search(T.left, x);
  12.     }
  13. }

统计树中结点的个数

树中结点的个数等于根节点(1) + 左子树结点个数 + 右子树的个数，递归求解即可。

  1. //统计结点个数
  2. static int count(Node T) {
  3.     if (T == null)
  4.         return 0;
  5.     else
  6.         return count(T.left) + count(T.right) + 1;
  7. }

计算树的高度

也是递归求解，左右子树的高度中的比较高的加上根节点就是树的高度。

  1. //计算二叉树的深度
  2. static int depth(Node T) {
  3.     if (T == null)
  4.         return 0;
  5.     return Math.max(depth(T.left), depth(T.right)) + 1;
  6. }

判断两棵树是不是相等

也是递归求解，两棵树相等，既要根节点的值相等，而且左右子树也要相等。

  1. //判断两棵树是不是相等
  2. static boolean is_SameTree(Node T1, Node T2) {
  3.     if (T1 == null && T2 == null)
  4.         return true;
  5.     else {
  6.         return T1 != null && T2 != null && T1.val == T2.val
  7.             && is_SameTree(T1.left, T2.left) && is_SameTree(T1.right, T2.right);
  8.     }
  9. }

完整测试代码

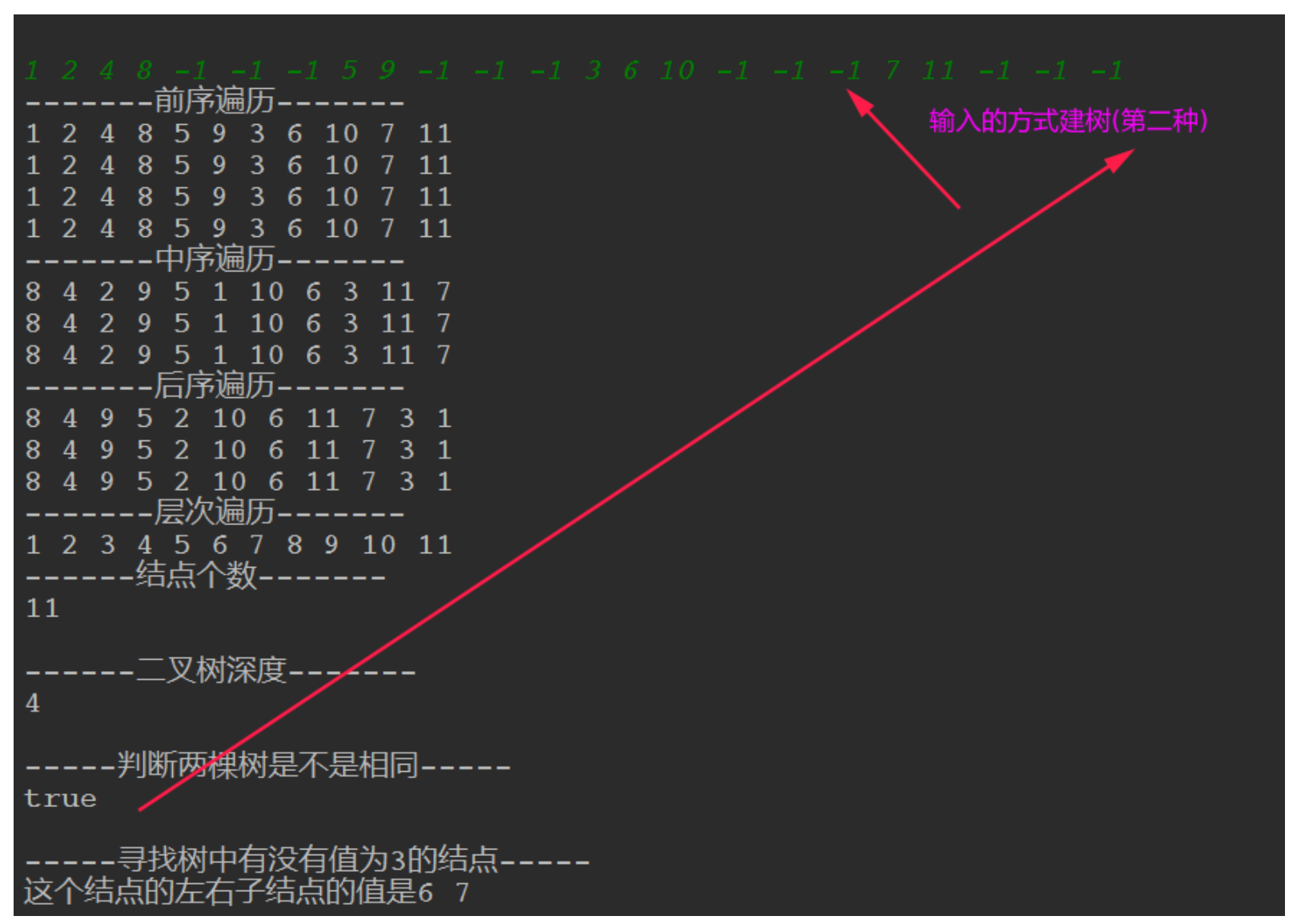
完整的测试代码，这里输入的样例树(就是建树的时候那个例子)如下:

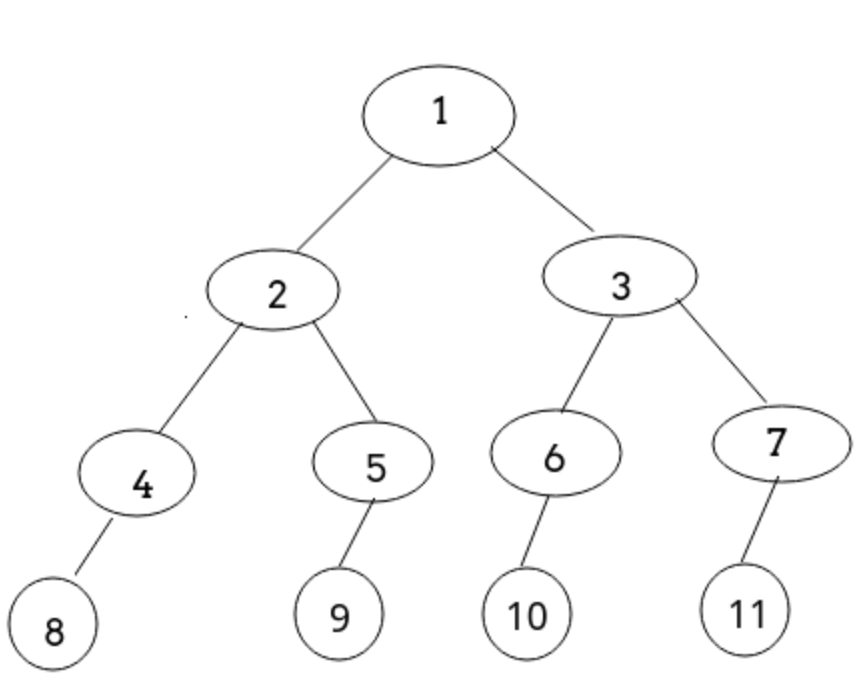
image.png

代码:

  1. import java.io.BufferedInputStream;
  2. import java.util.*;
  4. public class BinaryTree {
  6.     static class Node {
  7.         public int val;
  8.         public Node left;
  9.         public Node right;
  11.         public Node(int val) {
  12.             this.val = val;
  13.         }
  14.     }
  16.     // given a arr to build
  17.     static Node createTree(int arr[], int i) {
  18.         if (i >= arr.length || arr[i] == -1)
  19.             return null;
  20.         Node root = new Node(arr[i]);
  21.         root.left = createTree(arr, 2 * i + 1);
  22.         root.right = createTree(arr, 2 * i + 2);
  23.         return root;
  24.     }
  26.     // cin method    
  27.     static Node buildTree(Scanner cin) {
  28.         Node root = null;
  29.         int data = cin.nextInt();
  30.         if (data != -1) {
  31.             root = new Node(data);
  32.             root.left = buildTree(cin);
  33.             root.right = buildTree(cin);
  34.         }
  35.         return root;
  36.     }
  38.     static void preOrder(Node T) {
  39.         if (T == null)
  40.             return;
  41.         System.out.print(T.val + " ");
  42.         preOrder(T.left);
  43.         preOrder(T.right);
  44.     }
  46.     static void iterativePre(Node root) {
  47.         Stack<Node> s = new Stack<>();
  48.         Node p = root;
  49.         while (!s.empty() || p != null) {
  50.             if (p != null) {
  51.                 s.push(p);
  52.                 System.out.print(p.val + " ");
  53.                 p = p.left;
  54.             } else {
  55.                 p = s.pop();
  56.                 p = p.right;
  57.             }
  58.         }
  59.     }
  62.     static void iterativePre2(Node root) {
  63.         Stack<Node> s = new Stack<>();
  64.         Node p = root;
  65.         while (!s.empty() || p != null) {
  66.             while (p != null) { // while循环，直到左子树为空
  67.                 s.push(p);
  68.                 System.out.print(p.val + " ");
  69.                 p = p.left;
  70.             }
  71.             p = s.pop();
  72.             p = p.right;
  73.         }
  74.     }
  76.     /**
  77.      * 理解 :  push右子树，再push左子树，这样的话弹栈的时候就是先访问左子树，再右子树
  78.      */
  79.     static void iterativePre3(Node root) {
  80.         if (root == null)
  81.             return;
  82.         Node p = root;
  83.         Stack<Node> stack = new Stack<>();
  84.         stack.add(p);
  85.         while (!stack.isEmpty()) {
  86.             p = stack.pop();
  87.             System.out.print(p.val + " ");
  88.             if (p.right != null)
  89.                 stack.push(p.right);
  90.             if (p.left != null)
  91.                 stack.push(p.left);
  92.         }
  93.     }
  96.     static void inOrder(Node T) {
  97.         if (T == null)
  98.             return;
  99.         inOrder(T.left);
  100.         System.out.print(T.val + " ");
  101.         inOrder(T.right);
  102.     }
  104.     /**
  105.      * 1)、当前节点不空(!=null)，压入栈中(和前序遍历不同的是，不需要打印)，当前节点向左；
  106.      * 2)、当前节点为空(==null)，从栈中拿出一个并且打印(在这里打印) ，当前节点向右；
  107.      */
  108.     static void iterativeIn(Node root) {
  109.         if (root == null)
  110.             return;
  111.         Stack<Node> s = new Stack<>();
  112.         Node p = root;
  113.         while (!s.empty() || p != null) {
  114.             if (p != null) {
  115.                 s.push(p);
  116.                 p = p.left;
  117.             } else {
  118.                 p = s.pop();
  119.                 System.out.print(p.val + " "); //在这里打印
  120.                 p = p.right;
  121.             }
  122.         }
  123.     }
  125.     static void iterativeIn2(Node root) {
  126.         if (root == null)
  127.             return;
  128.         Stack<Node> s = new Stack<>();
  129.         Node p = root;
  130.         while (!s.empty() || p != null) {
  131.             while (p != null) { //这里改成while
  132.                 s.push(p);
  133.                 p = p.left;
  134.             }
  135.             p = s.pop();
  136.             System.out.print(p.val + " "); //在这里打印
  137.             p = p.right;
  138.         }
  139.     }
  142.     static void postOrder(Node T) {
  143.         if (T == null)
  144.             return;
  145.         postOrder(T.left);
  146.         postOrder(T.right);
  147.         System.out.print(T.val + " ");
  148.     }
  150.     /**
  151.      * 非递归后续1(双栈法解决非递归后续)
  152.      * 后续遍历是要实现　　　左->右->中
  153.      * 这个方法和前序遍历的第二种方法　只是多了一个栈而已
  154.      * 因为　前序遍历是  中->左->右　　压栈顺序是 右->左
  155.      * 这样，我们就很容易实现　中->右->左遍历　　压栈顺序是　左->右
  156.      * 而后续遍历是要实现  左->右->中，
  157.      * 我们把上面的　　中右左　压入到另一个栈中　就实现了　左右中
  158.      */
  159.     static void iterativePos(Node root) {
  160.         Stack<Node> s = new Stack<>(), s2 = new Stack<>();
  161.         Node p;
  162.         s.push(root);
  163.         while (!s.empty()) {
  164.             p = s.pop();
  165.             s2.push(p);
  166.             if (p.left != null) s.push(p.left); //这里是先左再右  (非递归前序是先右再左)
  167.             if (p.right != null) s.push(p.right);
  168.         }
  169.         while (!s2.empty())
  170.             System.out.print(s2.pop().val + " ");
  171.     }
  174.     /*** 非递归后续2(设置pre结点) */
  175.     static void iterativePos2(Node root) {
  176.         Node cur, pre = null;
  177.         Stack<Node> s = new Stack<>();
  178.         s.push(root);
  179.         while (!s.empty()) {
  180.             cur = s.peek();
  181.             // 两种可以访问的情况
  182.             if ((cur.left == null && cur.right == null) ||
  183.                     ((pre != null) && (pre == cur.left || pre == cur.right))) {
  184.                 System.out.print(cur.val + " ");
  185.                 s.pop();
  186.                 pre = cur;
  187.             } else {
  188.                 if (cur.right != null) s.push(cur.right);
  189.                 if (cur.left != null) s.push(cur.left);
  190.             }
  191.         }
  192.     }
  194.     static void levelOrder(Node root) {
  195.         if (root == null)
  196.             return;
  197.         Queue<Node> queue = new LinkedList<>();
  198.         queue.add(root);
  199.         while (!queue.isEmpty()) {
  200.             Node now = queue.poll();
  201.             System.out.print(now.val + " ");
  202.             if (now.left != null) queue.add(now.left);
  203.             if (now.right != null) queue.add(now.right);
  204.         }
  205.     }
  207.     //查找某个值为x的结点
  208.     static Node search(Node T, int x) {
  209.         if (T == null)
  210.             return null;
  211.         if (T.val == x)
  212.             return T;
  213.         else {
  214.             if (search(T.left, x) == null)
  215.                 return search(T.right, x);
  216.             else
  217.                 return search(T.left, x);
  218.         }
  219.     }
  221.     //统计结点个数
  222.     static int count(Node T) {
  223.         if (T == null)
  224.             return 0;
  225.         else
  226.             return count(T.left) + count(T.right) + 1;
  227.     }
  229.     //计算二叉树的深度
  230.     static int depth(Node T) {
  231.         if (T == null)
  232.             return 0;
  233.         return Math.max(depth(T.left), depth(T.right)) + 1;
  234.     }
  236.     //判断两棵树是不是相等
  237.     static boolean is_SameTree(Node T1, Node T2) {
  238.         if (T1 == null && T2 == null)
  239.             return true;
  240.         else {
  241.             return T1 != null && T2 != null && T1.val == T2.val
  242.                     && is_SameTree(T1.left, T2.left) && is_SameTree(T1.right, T2.right);
  243.         }
  244.     }
  246.     public static void main(String[] args) {
  247.         Scanner cin = new Scanner(new BufferedInputStream(System.in));
  248.         //        int[] arr = {1,2,3,4,5,6,7,8,-1,9,-1,10,-1,11,-1, -1,-1,-1,-1,-1,-1,-1,-1};
  249.         int[] arr = {1, 2, 3, 4, 5, 6, 7, 8, -1, 9, -1, 10, -1, 11, -1};
  250.         Node root = createTree(arr, 0);
  251.         //        树结构和上面相同,输入: 1 2 4 8 -1 -1 -1 5 9 -1 -1 -1 3 6 10 -1 -1 -1 7 11 -1 -1 -1
  252.         Node root2 = buildTree(cin);
  254.         System.out.println("-------前序遍历-------");
  255.         preOrder(root);
  256.         System.out.println();
  257.         iterativePre(root);
  258.         System.out.println();
  259.         iterativePre2(root);
  260.         System.out.println();
  261.         iterativePre3(root);
  263.         System.out.println("\n" + "-------中序遍历-------");
  264.         inOrder(root);
  265.         System.out.println();
  266.         iterativeIn(root);
  267.         System.out.println();
  268.         iterativeIn2(root);
  270.         System.out.println("\n" + "-------后序遍历-------");
  271.         postOrder(root);
  272.         System.out.println();
  273.         iterativePos(root);
  274.         System.out.println();
  275.         iterativePos2(root);
  277.         System.out.println("\n" + "-------层次遍历-------");
  278.         levelOrder(root);
  280.         System.out.println("\n" + "------结点个数-------");
  281.         System.out.println(count(root));
  283.         System.out.println("\n" + "------二叉树深度-------");
  284.         System.out.println(depth(root));
  286.         System.out.println("\n" + "-----判断两棵树是不是相同-----");
  287.         System.out.println(is_SameTree(root, root2));
  289.         System.out.println("\n" + "-----寻找树中有没有值为3的结点-----");
  290.         Node Find = search(root, 3);
  291.         if (null == Find)
  292.             System.out.println("没有找到结点");
  293.         else
  294.             System.out.println("这个结点的左右子结点的值是" + Find.left.val + " " + Find.right.val);
  295.     }
  296. }

运行效果如下图:

image.png