• 递归
  • 技巧的写法
  • 完整测试代码

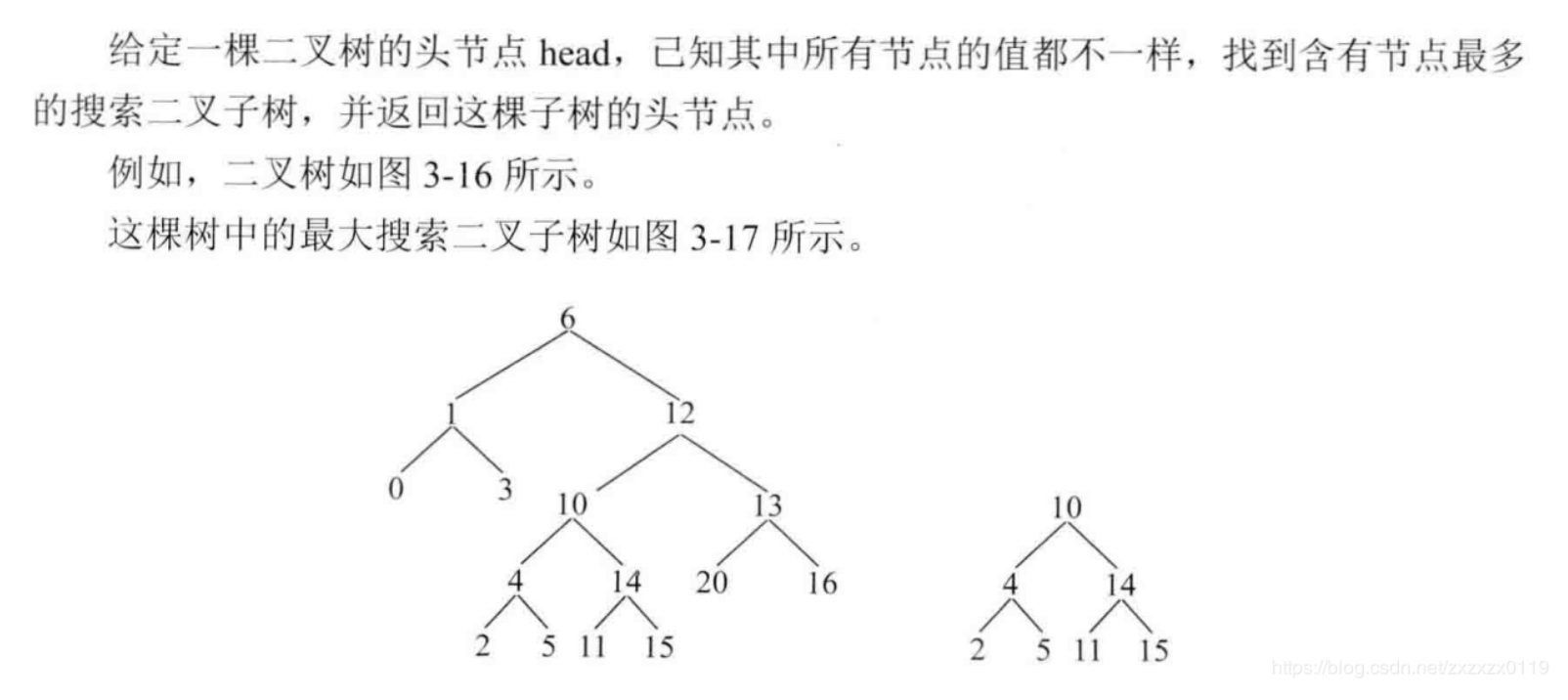
题目

image.png

递归

解析:
这种题目的解题过程分为三步:

  • 列出所有可能性；
  • 列出结点需要的信息，并整合信息(成一个结构体)；
  • 改递归 ，先假设左和右都给我信息(黑盒)，然后怎么利用左边和右边的信息组出来我该返回的信息，最后basecase(边界)填什么；

具体到这个题目：
第一步，列出所有可能性：

  • 第一种可能性，以node为头的结点的最大二叉搜索子树可能来自它左子树；
  • 第二种可能性，以node为头的结点的最大二叉搜索子树可能来自它右子树；
  • 第三种可能性，左树整体是搜索二叉树，右树整体也是搜索二叉树，而且左树的头是node.left，右树的头是node.right，且左树的最大值< node.value，右树的最小值> node.value， 那么以我为头的整棵树都是搜索二叉树；

第二步，列出结点需要的信息:

  • 信息一: 左树最大搜索二叉树大小；
  • 信息二: 右树最大搜索二叉树大小；
  • 信息三: 左树上最大搜索二叉树的头部是什么；
  • 信息四: 右树上最大搜索二叉树的头部是什么；
  • 信息五: 左树上的最大值；
  • 信息六: 右树上的最小值；

整合成一个Pair结构: 信息一和信息二整合：size ，信息三和信息四整合 : head(结点类型)，以及信息五和信息六 ；

  1.     //返回的类型
  2.     static class Pair {
  3.         public int size; //左右子树的大小
  4.         public Node root; //左右子树的头
  5.         public int min;
  6.         public int max;
  7.     }

然后第三部就是改成递归，具体如下(是后序遍历的顺序(需要左右的信息来构造头部的信息)):

  1.     static class Node {
  2.         public int value;
  3.         public Node left;
  4.         public Node right;
  6.         public Node(int value) {
  7.             this.value = value;
  8.         }
  9.     }
  11.     //返回的类型
  12.     static class Pair {
  13.         public int size; //左右子树的大小
  14.         public Node root; //左右子树的头
  15.         public int min;
  16.         public int max;
  18.         public Pair(int size, Node root, int min, int max) {
  19.             this.size = size;
  20.             this.root = root;
  21.             this.min = min;
  22.             this.max = max;
  23.         }
  24.     }
  26.     static Node biggestSubBST(Node head) {
  27.         return rec(head).root;
  28.     }
  30.     static Pair rec(Node head) {
  31.         if (head == null)
  32.             return new Pair(0, null, Integer.MAX_VALUE, Integer.MIN_VALUE);
  33.         Pair L = rec(head.left);
  34.         Pair R = rec(head.right);
  35.         int msize =
  36.                 (L.root == head.left && R.root == head.right && L.max < head.value && R.min > head.value)
  37.                         ? L.size + R.size + 1 : 0;
  38.         int maxSize = Math.max(Math.max(L.size, R.size), msize);
  39.         Node mroot = L.size > R.size ? L.root : R.root;
  40.         if (maxSize == msize) mroot = head;
  41.         return new Pair(maxSize, mroot, Math.min(head.value, Math.min(L.min, R.min)),
  42.                 Math.max(head.value, Math.max(L.max, R.max)));
  43.     }

改造的写法

技巧的写法(使用一个数组来记录size,min,max):

  1.     static Node biggestSubBST2(Node head) {
  2.         int[] rec = new int[3];  //0 记录size 1记录min 2记录max
  3.         return rec2(head, rec);
  4.     }
  6.     static Node rec2(Node head, int[] rec) {
  7.         if (head == null) {
  8.             rec[0] = 0;
  9.             rec[1] = Integer.MAX_VALUE;
  10.             rec[2] = Integer.MIN_VALUE;
  11.             return null;
  12.         }
  13.         Node L = rec2(head.left, rec);
  14.         int lsize = rec[0], lmin = rec[1], lmax = rec[2];
  15.         Node R = rec2(head.right, rec);
  16.         int rsize = rec[0], rmin = rec[1], rmax = rec[2];
  17.         int msize = (L == head.left && R == head.right && lmax < head.value && rmin > head.value) ? lsize + rsize + 1 : 0;
  18.         int maxSize = Math.max(msize, Math.max(lsize, rsize));
  19.         Node root = lsize > rsize ? L : R;
  20.         if (msize == maxSize) root = head;
  21.         rec[0] = maxSize;
  22.         rec[1] = Math.min(head.value, Math.min(lmin, rmin));
  23.         rec[2] = Math.max(head.value, Math.max(lmax, rmax));
  24.         return root;
  25.     }

完整测试代码(测试样例)

  1. /**
  2.  * 返回一棵树中最大的二叉搜索子树的大小
  3.  */
  5. public class BiggestSubBST {
  7.     static class Node {
  8.         public int value;
  9.         public Node left;
  10.         public Node right;
  12.         public Node(int value) {
  13.             this.value = value;
  14.         }
  15.     }
  17.     //返回的类型
  18.     static class Pair {
  19.         public int size; //左右子树的大小
  20.         public Node root; //左右子树的头
  21.         public int min;
  22.         public int max;
  24.         public Pair(int size, Node root, int min, int max) {
  25.             this.size = size;
  26.             this.root = root;
  27.             this.min = min;
  28.             this.max = max;
  29.         }
  30.     }
  32.     static Node biggestSubBST(Node head) {
  33.         return rec(head).root;
  34.     }
  36.     static Pair rec(Node head) {
  37.         if (head == null)
  38.             return new Pair(0, null, Integer.MAX_VALUE, Integer.MIN_VALUE);
  39.         Pair L = rec(head.left);
  40.         Pair R = rec(head.right);
  41.         int msize =
  42.                 (L.root == head.left && R.root == head.right && L.max < head.value && R.min > head.value)
  43.                         ? L.size + R.size + 1 : 0;
  44.         int maxSize = Math.max(Math.max(L.size, R.size), msize);
  45.         Node mroot = L.size > R.size ? L.root : R.root;
  46.         if (maxSize == msize) mroot = head;
  47.         return new Pair(maxSize, mroot, Math.min(head.value, Math.min(L.min, R.min)),
  48.                 Math.max(head.value, Math.max(L.max, R.max)));
  49.     }
  52.     static Node biggestSubBST2(Node head) {
  53.         int[] rec = new int[3];  //0 记录size 1记录min 2记录max
  54.         return rec2(head, rec);
  55.     }
  57.     static Node rec2(Node head, int[] rec) {
  58.         if (head == null) {
  59.             rec[0] = 0;
  60.             rec[1] = Integer.MAX_VALUE;
  61.             rec[2] = Integer.MIN_VALUE;
  62.             return null;
  63.         }
  64.         Node L = rec2(head.left, rec);
  65.         int lsize = rec[0], lmin = rec[1], lmax = rec[2];
  66.         Node R = rec2(head.right, rec);
  67.         int rsize = rec[0], rmin = rec[1], rmax = rec[2];
  68.         int msize = (L == head.left && R == head.right && lmax < head.value && rmin > head.value) ? lsize + rsize + 1 : 0;
  69.         int maxSize = Math.max(msize, Math.max(lsize, rsize));
  70.         Node root = lsize > rsize ? L : R;
  71.         if (msize == maxSize) root = head;
  72.         rec[0] = maxSize;
  73.         rec[1] = Math.min(head.value, Math.min(lmin, rmin));
  74.         rec[2] = Math.max(head.value, Math.max(lmax, rmax));
  75.         return root;
  76.     }
  78.     //建立二叉树
  79.     static Node build(int[] arr, int index) {
  80.         if (index >= arr.length || arr[index] == -1) return null;
  81.         Node root = new Node(arr[index]);
  82.         root.left = build(arr, index * 2 + 1);
  83.         root.right = build(arr, index * 2 + 2);
  84.         return root;
  85.     }
  87.     /**
  88.      * @param head   传入的节点
  89.      * @param height 　　层数(根节点为0)
  90.      * @param to     表示的特定节点  H表示根节点   ^表示父亲节点在左上方　v表示父亲节点在左下方
  91.      * @param len    　　　指定每一个节点打印的宽度
  92.      */
  93.     static void printTree(Node head, int height, String to, int len) {
  94.         if (head == null) return;
  95.         printTree(head.right, height + 1, "v", len);
  97.         String val = to + head.value + to;  //两边指示的字符
  98.         int lenV = val.length();
  99.         int lenL = (len - lenV) / 2;  //左边的空格(分一半)
  100.         int lenR = len - lenV - lenL; // 右边的空格
  101.         System.out.println(getSpace(len * height) + getSpace(lenL) + val + getSpace(lenR));
  103.         printTree(head.left, height + 1, "^", len);
  104.     }
  106.     //获取指定的空格
  107.     static String getSpace(int len) {
  108.         StringBuffer str = new StringBuffer();
  109.         for (int i = 0; i < len; i++) str.append(" ");
  110.         return str.toString();
  111.     }
  114.     public static void main(String[] args) {
  115.         int[] arr = {6, 1, 12, 0, 3, 10, 13, -1, -1, -1, -1, 4, 14, 20, 16, -1, -1, -1, -1, -1, -1, -1, -1, 2, 5, 11, 15, -1, -1, -1, -1};
  116.         Node head = build(arr, 0);
  117.         printTree(head, 0, "H", 10);
  118.         System.out.println(biggestSubBST(head).value);
  119.         System.out.println(biggestSubBST2(head).value);
  120.     }
  121. }

二叉树打印见这个博客
测试效果:
image.png