平衡二叉树总结

• 平衡二叉树相关概念以及性质
• 平衡二叉树的类结构以及简单处理方法
• 获取树的高度以及计算平衡因子
• 判断树是不是BST和AVL
• LL型失衡以及右旋转
• RR型失衡以及左旋转
• LR型失衡以及处理方法
• RL型失衡以及处理方法
• add()和remove()中失衡处理调整
• 完整源码测试
• 使用LeetCode-350. Intersection of Two Arrays II测试代码

一、前言

• 在学二叉平衡树之前，可以先学一下二叉排序树。
• 如果对于四种旋转，实在想不清的可以看一下这个动态视频。

二、平衡二叉树相关概念以及性质

相关基本概念：

• 平衡二叉树是一种二叉排序树，：要么是一棵空树，要么左右都是平衡二叉树，且左子树和右子树深度之绝对值不超过1. 将二叉树上结点的左子树深度减去右子树深度的值称为平衡因子BF，那么平衡二叉树上的所有结点的平衡因子只可能是-1、0和1。只要二叉树上有一个结点的平衡因子的绝对值大于1，则该二叉树就是不平衡的。
• 距离插入结点最近的，且平衡因子的绝对值大于1的结点为根的子树，称为最小不平衡子树。其中我们可以记住两个名词， 发现者：即第一个发现这个结点两边的高度之差大于1(我们也叫做最小不平衡结点 : 距离插入节点最近的不平衡节点)。破坏者：即插入这个结点之后使得树不平衡的那个点。(看等下旋转的例子就知道)。

三、平衡二叉树的类结构以及简单处理方法

二叉平衡树和二叉排序树的结构定义差不多，这里增加了一个hegiht属性，表示每一个结点为根的子树的高度。
其中大部分方法已经在二叉搜索树和集合和映射中解释和实现过。

/**
 * 基于BST实现的AVL
 */
public class AVLTree<K extends Comparable<K>,V> {
    private class Node{
        public K key;
        public V value;
        public Node left,right;
        public int height; //每一个结点都要记录一下高度 --> 为了求出每个结点的平衡因子
        public Node(K key, V value) {
            this.key = key;
            this.value = value;
            this.left = null;
            this.right = null;
            height = 1; //默认的每个新结点(叶子结点)高度都是1
        }
    }
    private Node root;
    private int size;
    public AVLTree(){
        root = null;
        size = 0;
    }
    public int size(){
        return size;
    }
    public boolean isEmpty(){
        return size == 0;
    }
     //返回以node为根节点的二分搜索树中，key所在的结点
    public Node getNode(Node node,K key){
        if(node == null)
            return null;
        if(key.compareTo(node.key) == 0){
            return node;
        }else if(key.compareTo(node.key) < 0) {
            return getNode(node.left,key);
        }else {
            return getNode(node.right,key);
        }
    }
    public boolean contains(K key){
        return getNode(root,key) != null;
    }
    public V get(K key){
        Node node = getNode(root,key);
        return node == null ? null : node.value;
    }
    public void set(K key,V newValue){
        Node node = getNode(root,key);
        if(node == null)
            throw new IllegalArgumentException(key + " doesn't exist !");
        node.value = newValue;
    }
    // 返回以node 为根的二分搜索树 最小值所在的结点
    private Node minumum(Node node){
        if(node.left == null)
            return node;
        return minumum(node.left);
    }
    //移除以node为根的二叉搜索树中最小值的结点，返回删除结点之后新的二叉搜索树的根
    private Node removeMin(Node node){
        if(node.left == null){
            Node rightNode = node.right;
            node.right = null;
            size--;
            return rightNode;
        }
        node.left = removeMin(node.left); //递归 and connect   例如下面返回一个rightNode, 我的left就连接上它
        return node;
    }
}

三、获取树的高度以及计算平衡因子

这两个方法很简单，平衡因子就是 左子树高度 - 右子树高度。

　  private int getHeight(Node node){
        if(node == null)return 0; //空树的高度是0
        return node.height;
    }
    //计算平衡因子 : 左子树高度-右子树高度
    private int getBalanceFactor(Node node){
        if(node == null)return 0;
        return getHeight(node.left) - getHeight(node.right);
    }

四、判断树是不是BST和AVL

这两个方法我在这篇博客和这篇博客中也写过，这里判断BST使用的是递归，原理都是利用了中序遍历和BST的性质。判断平衡二叉树就更简单了。

    //判断一棵树是不是二叉搜索树
   private boolean isBST(){
        ArrayList<K>keys = new ArrayList<>();
        inOrder(root,keys);
        for(int i = 1; i < keys.size(); i++){
            if(keys.get(i-1).compareTo(keys.get(i)) > 0)return false;
        }
        return true;
    }
    //递归中序
    private void inOrder(Node node, ArrayList<K> keys) {
        if(node == null )return;
        inOrder(node.left,keys);
        keys.add(node.key);
        inOrder(node.right,keys);
    }

    //判断这颗二叉树是不是平衡二叉树
    private boolean isBalanced(){
        return isBalanced(root);
    }
    private boolean isBalanced(Node node) { // self is balance and child is balance
        if(node == null)
            return true; // empty tree is a balance tree
        if(Math.abs(getBalanceFactor(node)) > 1)
            return false;
        return isBalanced(node.left) && isBalanced(node.right);
    }

五、LL型失衡以及右旋转

LL失衡就是破坏者是发现者的左孩子的左孩子 :

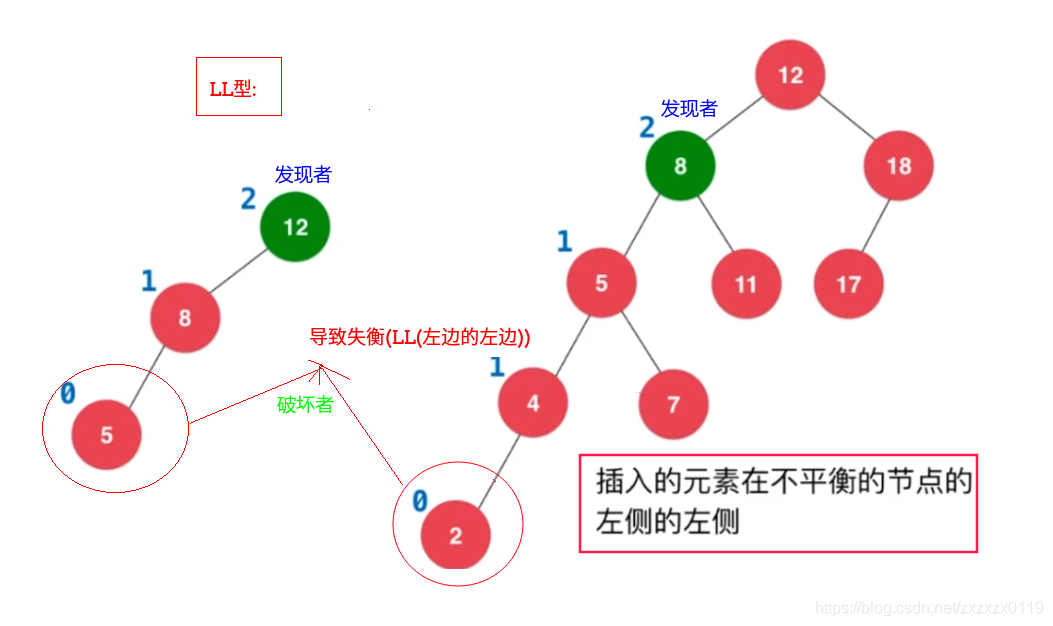
解决的办法:

• ① 先将T3(x的右孩子结点或者子树)扔到一边；
• ② 将以y为根的树顺时针旋转下来，接到x的右孩子；
• ③ 然后将T3放到y的左孩子地方；
• ④ 调整完之后记得更新高度；

① 先将T3(x的右孩子结点或者子树)扔到一边:

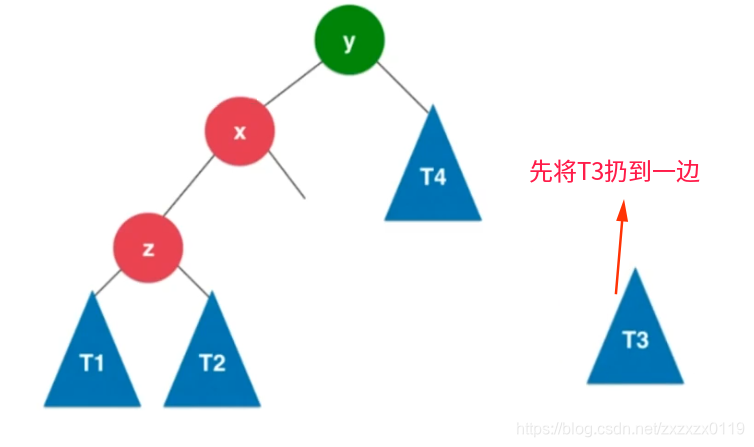
② 将以y为根的树顺时针旋转下来，接到x的右孩子:

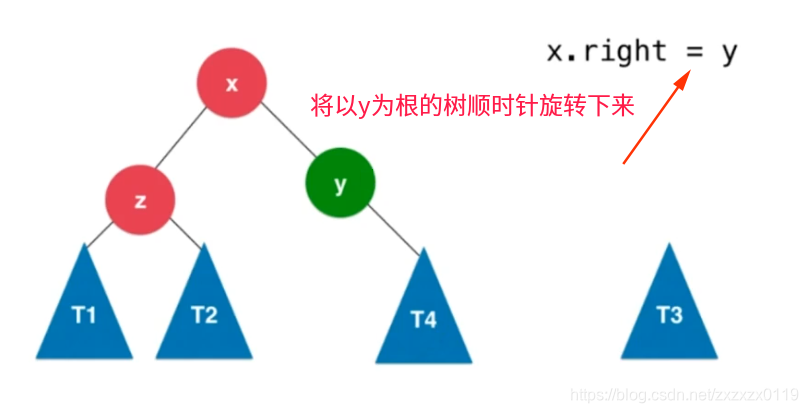
③ 然后将T3放到y的左孩子地方:

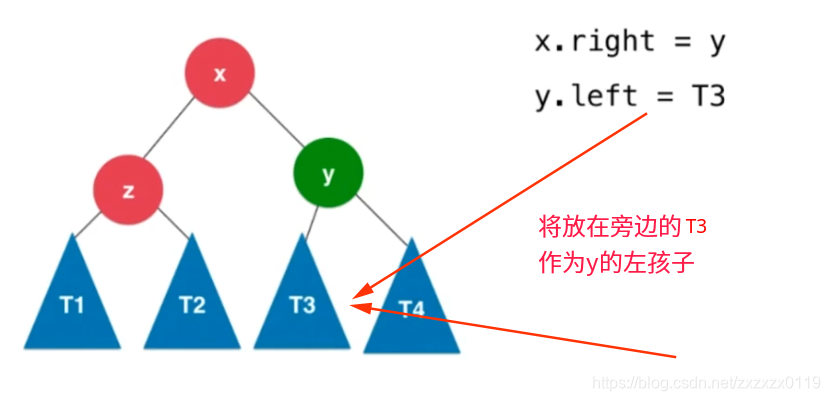
更新的前后关系如下:

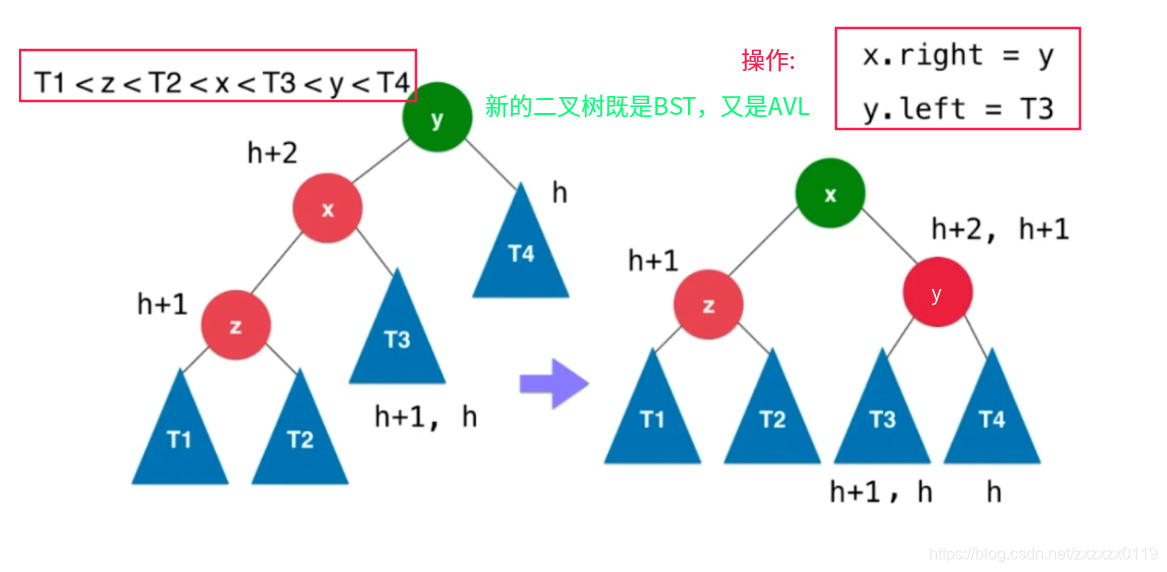
代码很简单:

  /** 对节点y进行向右旋转操作，返回旋转后新的根节点x
        右旋转   y                              x
               / \                           /   \
              x   T4     向右旋转 (y)        z     y
             / \       - - - - - - - ->    / \   / \
            z   T3                       T1  T2 T3 T4
           / \
         T1   T2
     */
    private Node rightRotate(Node y){ // y是失衡点
        Node x = y.left;
        Node T3 = x.right;
        x.right = y;
        y.left = T3;
        //调整之后需要更新height  注意要先更新y的height
        y.height = 1 + Math.max(getHeight(y.left),getHeight(y.right));
        x.height = 1 + Math.max(getHeight(x.left),getHeight(x.right));
        return x;
    }

六、RR型失衡以及左旋转

RR型失衡和LL型失衡对应，破坏者是发现者的右孩子的右孩子:

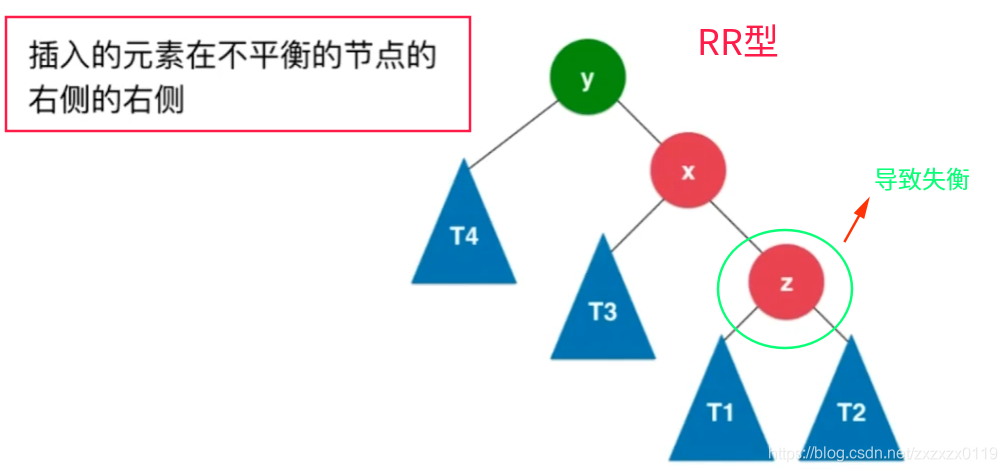
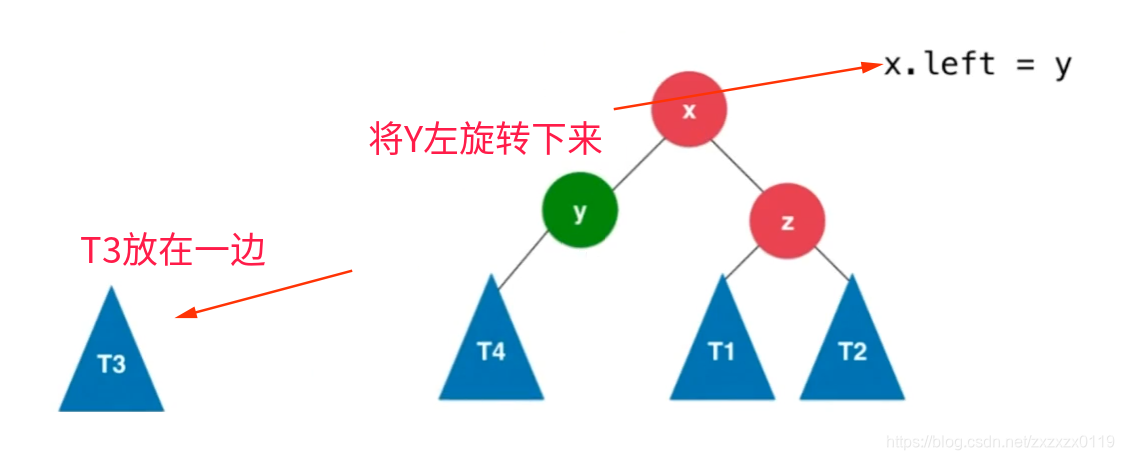
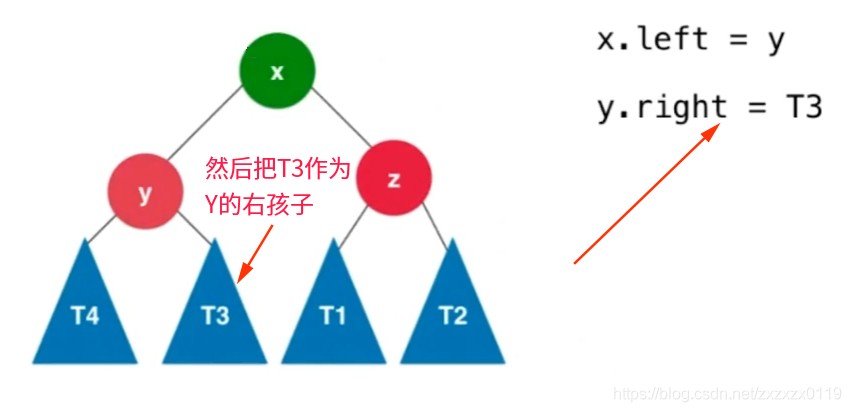
代码:

 /** 对节点y进行向左旋转操作，返回旋转后新的根节点x
            y                             x
          /  \                          /   \
         T4   x      向左旋转 (y)       y     z
             / \   - - - - - - - ->   / \   / \
           T3  z                     T4 T3 T1 T2
              / \
             T1 T2
    */
    private Node leftRotate(Node y){
        Node x = y.right;
        Node T3 = x.left;
        x.left = y;
        y.right = T3;
        //更新height
        y.height = 1 + Math.max(getHeight(y.left),getHeight(y.right));
        x.height = 1 + Math.max(getHeight(x.left),getHeight(x.right));
        return x;
    }

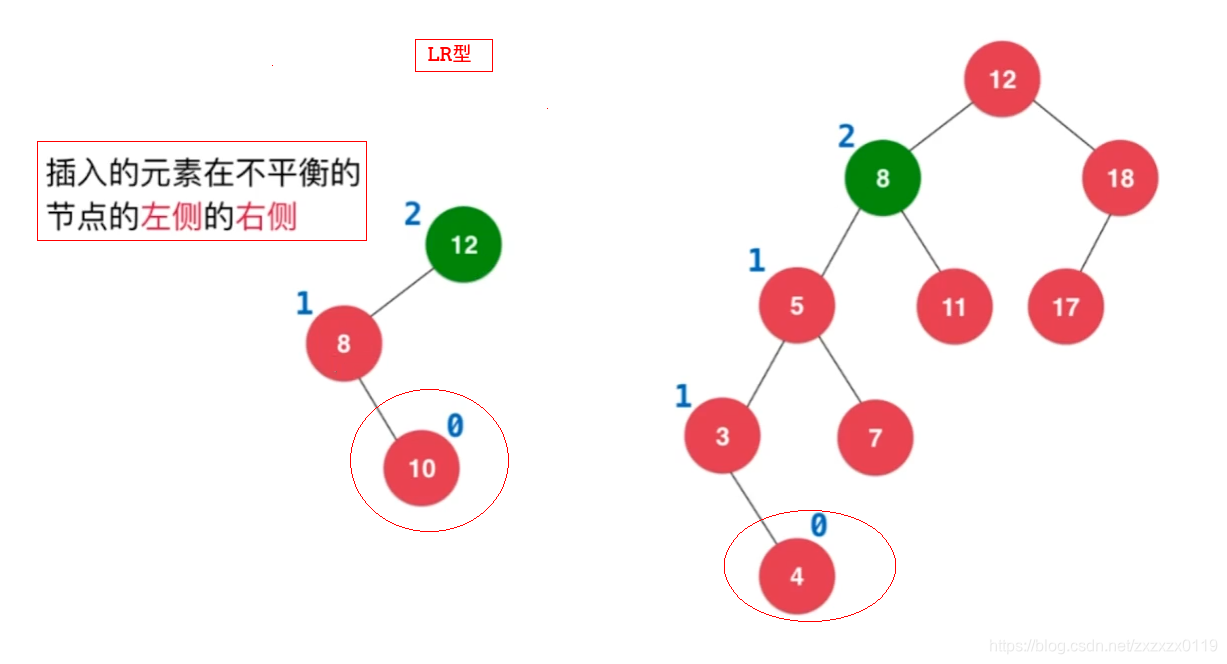
七、LR型失衡以及处理方法

LR型就是破坏者是node的左孩子的右孩子。处理方法要分为两部:

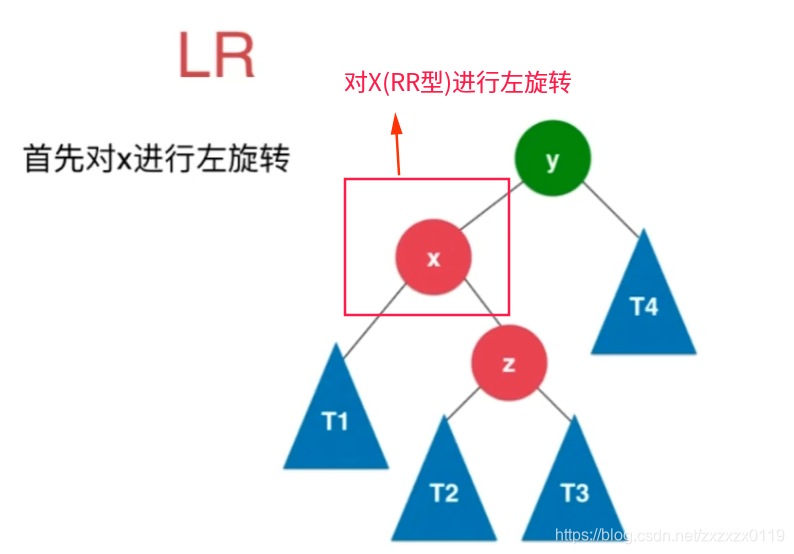
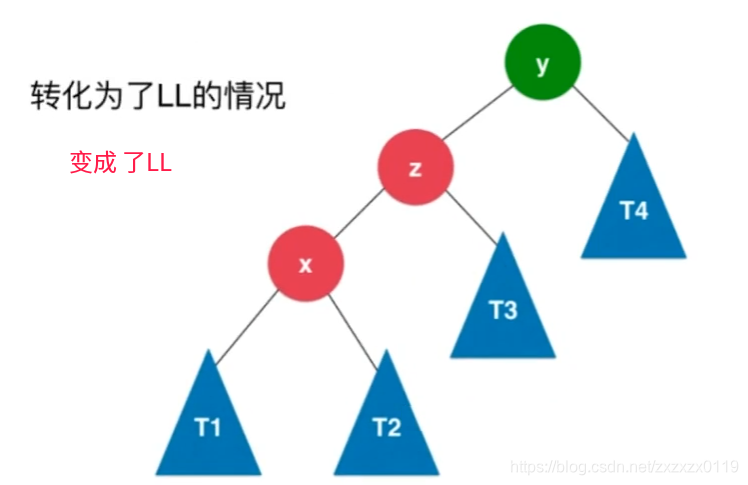
• 先对node的左孩子进行左旋转，变成LL型；
• 然后对node自己进行右旋转即可。

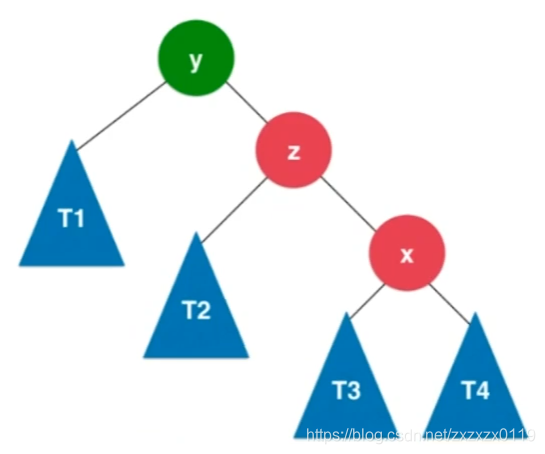
八、RL型失衡以及处理方法

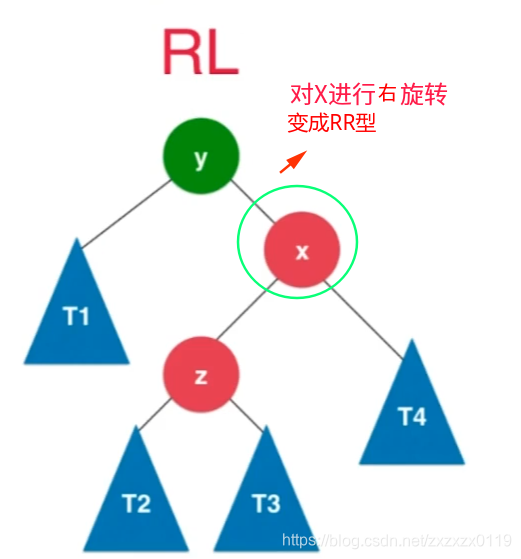
同理，和LR型对称的，RL型就是破坏者是node的右孩子的左孩子。处理方法:

• 先对node.right进行右旋转(rightRotate)变成RR型；
• 然后对自己进行左旋转即可。

九、add()和remove()中失衡处理调整

我们在插入或者移除元素时有可能会破坏二叉树的平衡性，所以需要调整，调整步骤:

• 先更新height；
• 计算平衡因子；
• 判断失衡类型；

其中判断失衡类型总共有四种　:

假设int balanceFactor = getBalanceFactor(node);也就是balanceFactor是node的平衡因子。

• LL型，balanceFactor > 1 && getBalanceFactor(node.left) >= 0；
• RR型，balanceFactor < -1 && getBalanceFactor(node.right) <= 0；
• LR型，balanceFactor > 1 && getBalanceFactor(node.left) < 0；
• RL型，balanceFactor < -1 && getBalanceFactor(node.right) > 0；

其中add()添加元素和二叉搜索树区别不大，就是这里存储的是键值对<K，V>映射，而之前的二叉搜索树存储的是集合，相当于JDK中TreeSet和TreeMap一样的区别。

 //向AVL树中添加新的元素(key,valu)
    public void add(K key,V value){
        root = add(root,key,value);
    }
    private Node add(Node node,K key,V value){
        if(node == null){
            size++;
            return new Node(key, value); //新建默认高度是height = 1
        }
        if(key.compareTo(node.key) < 0){
            node.left = add(node.left,key,value);
        }else if(key.compareTo(node.key) > 0){
            node.right = add(node.right,key,value);
        }else {  // update
            node.value = value;
        }
        /** 1) 更新height */
        node.height =  1 + Math.max(getHeight(node.left), getHeight(node.right));
        /** 2)计算平衡因子  */
        int balanceFactor = getBalanceFactor(node);
        /** 3)调整  : 分为四种情况下的调整*/
        /** LL型  */
        if(balanceFactor > 1 && getBalanceFactor(node.left) >= 0)
            return rightRotate(node);
        /** RR型  */
        if(balanceFactor < -1 && getBalanceFactor(node.right) <= 0){
            return leftRotate(node);
        }
        /** LR型  */
        if(balanceFactor > 1 && getBalanceFactor(node.left) < 0){
            node.left = leftRotate(node.left); //左孩子先进行左旋转
            return rightRotate(node);  //自己再进行右旋转
        }
        /** RL型  */
        if(balanceFactor < -1 && getBalanceFactor(node.right) > 0){
            node.right = rightRotate(node.right); //右孩子先进行右旋转
            return leftRotate(node);  //自己再进行左旋转
        }
        return node;
    }

remove方法和之前的二叉搜索树中实现的remove方法稍微有点不同:

• 因为我们在remove之后要调整平衡，所以使用了一个retNode来存储各种操作之后要返回的node，最后统一调整；
• 在调整之前判断一下retNode是否为null，如果是null的话不能操作，否则抛出空指针异常；
• 有一个bug，如果还是使用之前的removeMin来处理在删除一个左右孩子都全的node的时候，在removeMin中没有进行平衡的调整，所以我们在node.right中删除successor的时候使用的是递归的删除，也就是调用自己的remove方法。
• 在key.compareTo(node.key) == 0的时候，也就是else 中要删除node的三个逻辑要互斥的处理，不然会重复，因为不是直接返回，和二叉搜索树的处理不同，要注意。

    public V remove(K key){
        Node node = getNode(root,key);
        if(node != null){
            root = remove(root,key);
            return node.value;
        }
        return null;
    }
    private Node remove(Node node, K key){
        if(node == null)return null;
        Node retNode = null;
        if(key.compareTo(node.key) < 0){
            node.left = remove(node.left,key);
            retNode = node;
        }else if(key.compareTo(node.key) > 0){
            node.right = remove(node.right,key);
            retNode = node;
        }else {
            //和BST不同　三种情况是一个互斥的关系
            if(node.left == null){
                Node rightNode = node.right;
                node.right = null;
                size--;
                retNode = rightNode;
            }else if(node.right == null){
                Node leftNode = node.left;
                node.left = null;
                size--;
                retNode = leftNode;
            }else {
                Node successor = minumum(node.right);
//                successor.right = removeMin(node.right);  //这里和BST 不同，这里有可能会破坏平衡，所以不用这个
                successor.right = remove(node.right,successor.key); /**这里自己可以维护平衡*/
                successor.left = node.left;
                node.right = node.left = null;
                retNode = successor;
            }
        }
        /**特判 和　BST不同*/
        if(retNode == null)return null;
        /** 1) 更新height */
        retNode.height =  1 + Math.max(getHeight(retNode.left), getHeight(retNode.right));
        /** 2)计算平衡因子  */
        int balanceFactor = getBalanceFactor(retNode);
        /** 3)调整  : 分为四种情况下的调整*/
        /** LL型  */
        if(balanceFactor > 1 && getBalanceFactor(retNode.left) >= 0)
            return rightRotate(retNode);
        /** RR型  */
        if(balanceFactor < -1 && getBalanceFactor(retNode.right) <= 0){
            return leftRotate(retNode);
        }
        /** LR型  */
        if(balanceFactor > 1 && getBalanceFactor(retNode.left) < 0){
            retNode.left = leftRotate(retNode.left); //左孩子先进行左旋转
            return rightRotate(retNode);  //自己再进行右旋转
        }
        /** RL型  */
        if(balanceFactor < -1 && getBalanceFactor(retNode.right) > 0){
            retNode.right = rightRotate(retNode.right); //右孩子先进行右旋转
            return leftRotate(retNode);  //自己再进行左旋转
        }
        return retNode;
    }

十、完整源码测试

import java.util.ArrayList;
import java.util.Arrays;
/**
 * 基于BST实现的AVL
 */
public class AVLTree<K extends Comparable<K>,V> {
    private class Node{
        public K key;
        public V value;
        public Node left,right;
        public int height; //每一个结点都要记录一下高度 --> 为了求出每个结点的平衡因子
        public Node(K key, V value) {
            this.key = key;
            this.value = value;
            this.left = null;
            this.right = null;
            height = 1; //默认的每个新结点(叶子结点)高度都是1
        }
    }
    private Node root;
    private int size;
    public AVLTree(){
        root = null;
        size = 0;
    }
    public int size(){
        return size;
    }
    public boolean isEmpty(){
        return size == 0;
    }
    private int getHeight(Node node){
        if(node == null)return 0; //空树的高度是0
        return node.height;
    }
    //计算平衡因子 : 左子树高度-右子树高度
    private int getBalanceFactor(Node node){
        if(node == null)return 0;
        return getHeight(node.left) - getHeight(node.right);
    }
    //判断一棵树是不是二叉搜索树
    private boolean isBST(){
        ArrayList<K>keys = new ArrayList<>();
        inOrder(root,keys);
        for(int i = 1; i < keys.size(); i++){
            if(keys.get(i-1).compareTo(keys.get(i)) > 0)return false;
        }
        return true;
    }
    private void inOrder(Node node, ArrayList<K> keys) {
        if(node == null )return;
        inOrder(node.left,keys);
        keys.add(node.key);
        inOrder(node.right,keys);
    }
    //判断这颗二叉树是不是平衡二叉树
    private boolean isBalanced(){
        return isBalanced(root);
    }
    private boolean isBalanced(Node node) { // self is balance and child is balance
        if(node == null)return true; // empty tree is a balance tree
        if(Math.abs(getBalanceFactor(node)) > 1)return false;
        return isBalanced(node.left) && isBalanced(node.right);
    }
    /** 对节点y进行向右旋转操作，返回旋转后新的根节点x
        右旋转   y                              x
               / \                           /   \
              x   T4     向右旋转 (y)        z     y
             / \       - - - - - - - ->    / \   / \
            z   T3                       T1  T2 T3 T4
           / \
         T1   T2
     */
    private Node rightRotate(Node y){ // y是失衡点
        Node x = y.left;
        Node T3 = x.right;
        x.right = y;
        y.left = T3;
        //调整之后需要更新height  注意要先更新y的height
        y.height = 1 + Math.max(getHeight(y.left),getHeight(y.right));
        x.height = 1 + Math.max(getHeight(x.left),getHeight(x.right));
        return x;
    }
    /** 对节点y进行向左旋转操作，返回旋转后新的根节点x
            y                             x
          /  \                          /   \
         T4   x      向左旋转 (y)       y     z
             / \   - - - - - - - ->   / \   / \
           T3  z                     T4 T3 T1 T2
              / \
             T1 T2
    */
    private Node leftRotate(Node y){
        Node x = y.right;
        Node T3 = x.left;
        x.left = y;
        y.right = T3;
        //更新height
        y.height = 1 + Math.max(getHeight(y.left),getHeight(y.right));
        x.height = 1 + Math.max(getHeight(x.left),getHeight(x.right));
        return x;
    }
    //向AVL树中添加新的元素(key,valu)
    public void add(K key,V value){
        root = add(root,key,value);
    }
    private Node add(Node node,K key,V value){
        if(node == null){
            size++;
            return new Node(key, value); //新建默认高度是height = 1
        }
        if(key.compareTo(node.key) < 0){
            node.left = add(node.left,key,value);
        }else if(key.compareTo(node.key) > 0){
            node.right = add(node.right,key,value);
        }else {  // update
            node.value = value;
        }
        /** 1) 更新height */
        node.height =  1 + Math.max(getHeight(node.left), getHeight(node.right));
        /** 2)计算平衡因子  */
        int balanceFactor = getBalanceFactor(node);
        /** 3)调整  : 分为四种情况下的调整*/
        /** LL型  */
        if(balanceFactor > 1 && getBalanceFactor(node.left) >= 0)
            return rightRotate(node);
        /** RR型  */
        if(balanceFactor < -1 && getBalanceFactor(node.right) <= 0){
            return leftRotate(node);
        }
        /** LR型  */
        if(balanceFactor > 1 && getBalanceFactor(node.left) < 0){
            node.left = leftRotate(node.left); //左孩子先进行左旋转
            return rightRotate(node);  //自己再进行右旋转
        }
        /** RL型  */
        if(balanceFactor < -1 && getBalanceFactor(node.right) > 0){
            node.right = rightRotate(node.right); //右孩子先进行右旋转
            return leftRotate(node);  //自己再进行左旋转
        }
        return node;
    }
    //返回以node为根节点的二分搜索树中，key所在的结点
    public Node getNode(Node node,K key){
        if(node == null)
            return null;
        if(key.compareTo(node.key) == 0){
            return node;
        }else if(key.compareTo(node.key) < 0) {
            return getNode(node.left,key);
        }else {
            return getNode(node.right,key);
        }
    }
    public boolean contains(K key){
        return getNode(root,key) != null;
    }
    public V get(K key){
        Node node = getNode(root,key);
        return node == null ? null : node.value;
    }
    public void set(K key,V newValue){
        Node node = getNode(root,key);
        if(node == null)
            throw new IllegalArgumentException(key + " doesn't exist !");
        node.value = newValue;
    }
    // 返回以node 为根的二分搜索树 最小值所在的结点
    private Node minumum(Node node){
        if(node.left == null)
            return node;
        return minumum(node.left);
    }
    //移除以node为根的二叉搜索树中最小值的结点，返回删除结点之后新的二叉搜索树的根
    private Node removeMin(Node node){
        if(node.left == null){
            Node rightNode = node.right;
            node.right = null;
            size--;
            return rightNode;
        }
        node.left = removeMin(node.left); //递归 and connect   例如下面返回一个rightNode, 我的left就连接上它
        return node;
    }
    public V remove(K key){
        Node node = getNode(root,key);
        if(node != null){
            root = remove(root,key);
            return node.value;
        }
        return null;
    }
    private Node remove(Node node, K key){
        if(node == null)return null;
        Node retNode = null;
        if(key.compareTo(node.key) < 0){
            node.left = remove(node.left,key);
            retNode = node;
        }else if(key.compareTo(node.key) > 0){
            node.right = remove(node.right,key);
            retNode = node;
        }else {
            //和BST不同　三种情况是一个互斥的关系
            if(node.left == null){
                Node rightNode = node.right;
                node.right = null;
                size--;
                retNode = rightNode;
            }else if(node.right == null){
                Node leftNode = node.left;
                node.left = null;
                size--;
                retNode = leftNode;
            }else {
                Node successor = minumum(node.right);
//                successor.right = removeMin(node.right);  //这里和BST 不同，这里有可能会破坏平衡，所以不用这个
                successor.right = remove(node.right,successor.key); /**这里自己可以维护平衡*/
                successor.left = node.left;
                node.right = node.left = null;
                retNode = successor;
            }
        }
        /**特判 和　BST不同*/
        if(retNode == null)return null;
        /** 1) 更新height */
        retNode.height =  1 + Math.max(getHeight(retNode.left), getHeight(retNode.right));
        /** 2)计算平衡因子  */
        int balanceFactor = getBalanceFactor(retNode);
        /** 3)调整  : 分为四种情况下的调整*/
        /** LL型  */
        if(balanceFactor > 1 && getBalanceFactor(retNode.left) >= 0)
            return rightRotate(retNode);
        /** RR型  */
        if(balanceFactor < -1 && getBalanceFactor(retNode.right) <= 0){
            return leftRotate(retNode);
        }
        /** LR型  */
        if(balanceFactor > 1 && getBalanceFactor(retNode.left) < 0){
            retNode.left = leftRotate(retNode.left); //左孩子先进行左旋转
            return rightRotate(retNode);  //自己再进行右旋转
        }
        /** RL型  */
        if(balanceFactor < -1 && getBalanceFactor(retNode.right) > 0){
            retNode.right = rightRotate(retNode.right); //右孩子先进行右旋转
            return leftRotate(retNode);  //自己再进行左旋转
        }
        return retNode;
    }
    public void printTree(){
        printTree(root,0,"H",8);
    }
    public void printTree(Node head,int height,String to,int len){
        if(head == null)return;
        printTree(head.right,height + 1,"v",len);
        String val = to + head.key + to;  //两边指示的字符
        int lenV = val.length();
        int lenL = (len - lenV)/2;  //左边的空格(分一半)
        int lenR = len - lenV - lenL; // 右边的空格
        System.out.println( getSpace(len * height) + getSpace(lenL) + val + getSpace(lenR));
        printTree(head.left,height + 1,"^",len);
    }
    public static String getSpace(int len){
        StringBuffer str = new StringBuffer();
        for(int i = 0; i < len; i++) str.append(" ");
        return str.toString();
    }
    /**
     * for test
     */
    public static void main(String[] args) {
        Integer[] arr = {21,14,28,11,18,25,32,5,12,15,19,23,27,30,37};
        Arrays.sort(arr);
        AVLTree<Integer,Integer>avlTree = new AVLTree<>();
        for(int i = 0; i < arr.length; i++) avlTree.add(arr[i],null);
        avlTree.printTree();
        System.out.println(avlTree.isBalanced());
        System.out.println(avlTree.isBST());
    }
}

效果

• 打印二叉树见这个博客
• 值得注意的是，我在插入之前对arr进行了排序，如果是BST会退化成链表，如下图所示，但是这里的AVL不会；

十一、使用LeetCode-350. Intersection of Two Arrays II测试代码

为了保证AVLTree的正确性，使用LeetCode-350测试：

题目链接

题目

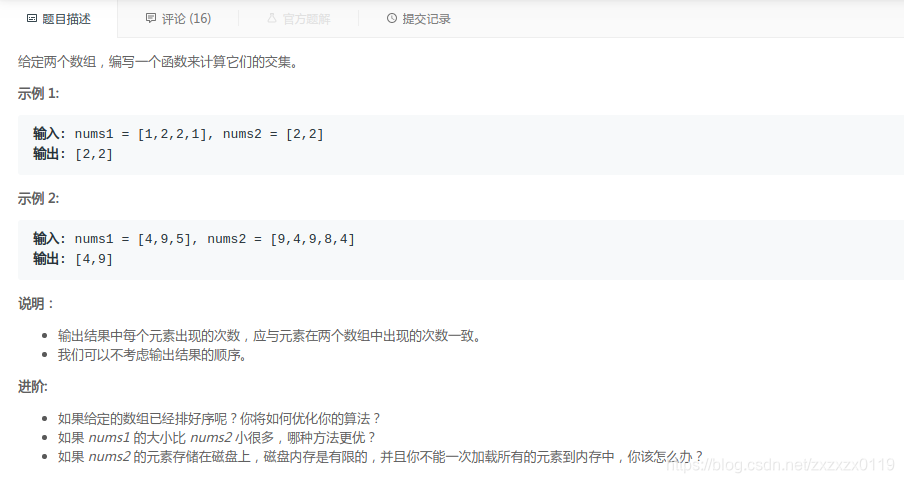
解析

使用 HashMap和TreeMap都能很简单的做出来，这里使用自己写的AVLTree测试一下:

import java.util.ArrayList;
class Solution {
      public int[] intersect(int[] nums1, int[] nums2) {
        AVLTree<Integer,Integer> map = new AVLTree<>();
        for(int num : nums1){
            if(!map.contains(num)) {
                map.add(num,1);
            }else {
                map.add(num, map.get(num) + 1);
            }
        }
        ArrayList<Integer>list = new ArrayList<>();
        for(int num : nums2){
            if(map.contains(num)){
                list.add(num);
                map.add(num,map.get(num) - 1);
                if(map.get(num) == 0)
                    map.remove(num);
            }
        }
        int[] res = new int[list.size()];
        for(int i = 0; i < list.size(); i++){
            res[i] = list.get(i);
        }
        return res;
    }
    /**
     * 基于BST实现的AVL
     */
    private class AVLTree<K extends Comparable<K>,V> {
        private class Node{
            public K key;
            public V value;
            public Node left,right;
            public int height; //每一个结点都要记录一下高度 --> 为了求出每个结点的平衡因子
            public Node(K key, V value) {
                this.key = key;
                this.value = value;
                this.left = null;
                this.right = null;
                height = 1; //默认的每个新结点(叶子结点)高度都是1
            }
        }
        private Node root;
        private int size;
        public AVLTree(){
            root = null;
            size = 0;
        }
        public int size(){
            return size;
        }
        public boolean isEmpty(){
            return size == 0;
        }
        private int getHeight(Node node){
            if(node == null)return 0; //空树的高度是0
            return node.height;
        }
        //计算平衡因子 : 左子树高度-右子树高度
        private int getBalanceFactor(Node node){
            if(node == null)return 0;
            return getHeight(node.left) - getHeight(node.right);
        }
        //判断一棵树是不是二叉搜索树
        private boolean isBST(){
            ArrayList<K>keys = new ArrayList<>();
            inOrder(root,keys);
            for(int i = 1; i < keys.size(); i++){
                if(keys.get(i-1).compareTo(keys.get(i)) > 0)return false;
            }
            return true;
        }
        private void inOrder(Node node, ArrayList<K> keys) {
            if(node == null )return;
            inOrder(node.left,keys);
            keys.add(node.key);
            inOrder(node.right,keys);
        }
        //判断这颗二叉树是不是平衡二叉树
        private boolean isBalanced(){
            return isBalanced(root);
        }
        private boolean isBalanced(Node node) { // self is balance and child is balance
            if(node == null)return true; // empty tree is a balance tree
            if(Math.abs(getBalanceFactor(node)) > 1)return false;
            return isBalanced(node.left) && isBalanced(node.right);
        }
        /** 对节点y进行向右旋转操作，返回旋转后新的根节点x
            右旋转   y                              x
                   / \                           /   \
                  x   T4     向右旋转 (y)        z     y
                 / \       - - - - - - - ->    / \   / \
                z   T3                       T1  T2 T3 T4
               / \
             T1   T2
         */
        private Node rightRotate(Node y){ // y是失衡点
            Node x = y.left;
            Node T3 = x.right;
            x.right = y;
            y.left = T3;
            //调整之后需要更新height  注意要先更新y的height
            y.height = 1 + Math.max(getHeight(y.left),getHeight(y.right));
            x.height = 1 + Math.max(getHeight(x.left),getHeight(x.right));
            return x;
        }
        /** 对节点y进行向左旋转操作，返回旋转后新的根节点x
                y                             x
              /  \                          /   \
             T4   x      向左旋转 (y)       y     z
                 / \   - - - - - - - ->   / \   / \
               T3  z                     T4 T3 T1 T2
                  / \
                 T1 T2
        */
        private Node leftRotate(Node y){
            Node x = y.right;
            Node T3 = x.left;
            x.left = y;
            y.right = T3;
            //更新height
            y.height = 1 + Math.max(getHeight(y.left),getHeight(y.right));
            x.height = 1 + Math.max(getHeight(x.left),getHeight(x.right));
            return x;
        }
        //向AVL树中添加新的元素(key,valu)
        public void add(K key,V value){
            root = add(root,key,value);
        }
        private Node add(Node node,K key,V value){
            if(node == null){
                size++;
                return new Node(key, value); //新建默认高度是height = 1
            }
            if(key.compareTo(node.key) < 0){
                node.left = add(node.left,key,value);
            }else if(key.compareTo(node.key) > 0){
                node.right = add(node.right,key,value);
            }else {  // update
                node.value = value;
            }
            /** 1) 更新height */
            node.height =  1 + Math.max(getHeight(node.left), getHeight(node.right));
            /** 2)计算平衡因子  */
            int balanceFactor = getBalanceFactor(node);
            /** 3)调整  : 分为四种情况下的调整*/
            /** LL型  */
            if(balanceFactor > 1 && getBalanceFactor(node.left) >= 0)
                return rightRotate(node);
            /** RR型  */
            if(balanceFactor < -1 && getBalanceFactor(node.right) <= 0){
                return leftRotate(node);
            }
            /** LR型  */
            if(balanceFactor > 1 && getBalanceFactor(node.left) < 0){
                node.left = leftRotate(node.left); //左孩子先进行左旋转
                return rightRotate(node);  //自己再进行右旋转
            }
            /** RL型  */
            if(balanceFactor < -1 && getBalanceFactor(node.right) > 0){
                node.right = rightRotate(node.right); //右孩子先进行右旋转
                return leftRotate(node);  //自己再进行左旋转
            }
            return node;
        }
        //返回以node为根节点的二分搜索树中，key所在的结点
        public Node getNode(Node node,K key){
            if(node == null)
                return null;
            if(key.compareTo(node.key) == 0){
                return node;
            }else if(key.compareTo(node.key) < 0) {
                return getNode(node.left,key);
            }else {
                return getNode(node.right,key);
            }
        }
        public boolean contains(K key){
            return getNode(root,key) != null;
        }
        public V get(K key){
            Node node = getNode(root,key);
            return node == null ? null : node.value;
        }
        public void set(K key,V newValue){
            Node node = getNode(root,key);
            if(node == null)
                throw new IllegalArgumentException(key + " doesn't exist !");
            node.value = newValue;
        }
        // 返回以node 为根的二分搜索树 最小值所在的结点
        private Node minumum(Node node){
            if(node.left == null)
                return node;
            return minumum(node.left);
        }
        //移除以node为根的二叉搜索树中最小值的结点，返回删除结点之后新的二叉搜索树的根
        private Node removeMin(Node node){
            if(node.left == null){
                Node rightNode = node.right;
                node.right = null;
                size--;
                return rightNode;
            }
            node.left = removeMin(node.left); //递归 and connect   例如下面返回一个rightNode, 我的left就连接上它
            return node;
        }
        public V remove(K key){
            Node node = getNode(root,key);
            if(node != null){
                root = remove(root,key);
                return node.value;
            }
            return null;
        }
        private Node remove(Node node, K key){
            if(node == null)return null;
            Node retNode = null;
            if(key.compareTo(node.key) < 0){
                node.left = remove(node.left,key);
                retNode = node;
            }else if(key.compareTo(node.key) > 0){
                node.right = remove(node.right,key);
                retNode = node;
            }else {
                //和BST不同　三种情况是一个互斥的关系
                if(node.left == null){
                    Node rightNode = node.right;
                    node.right = null;
                    size--;
                    retNode = rightNode;
                }else if(node.right == null){
                    Node leftNode = node.left;
                    node.left = null;
                    size--;
                    retNode = leftNode;
                }else {
                    Node successor = minumum(node.right);
    //                successor.right = removeMin(node.right);  //这里和BST 不同，这里有可能会破坏平衡，所以不用这个
                    successor.right = remove(node.right,successor.key); /**这里自己可以维护平衡*/
                    successor.left = node.left;
                    node.right = node.left = null;
                    retNode = successor;
                }
            }
            /**特判 和　BST不同*/
            if(retNode == null)return null;
            /** 1) 更新height */
            retNode.height =  1 + Math.max(getHeight(retNode.left), getHeight(retNode.right));
            /** 2)计算平衡因子  */
            int balanceFactor = getBalanceFactor(retNode);
            /** 3)调整  : 分为四种情况下的调整*/
            /** LL型  */
            if(balanceFactor > 1 && getBalanceFactor(retNode.left) >= 0)
                return rightRotate(retNode);
            /** RR型  */
            if(balanceFactor < -1 && getBalanceFactor(retNode.right) <= 0){
                return leftRotate(retNode);
            }
            /** LR型  */
            if(balanceFactor > 1 && getBalanceFactor(retNode.left) < 0){
                retNode.left = leftRotate(retNode.left); //左孩子先进行左旋转
                return rightRotate(retNode);  //自己再进行右旋转
            }
            /** RL型  */
            if(balanceFactor < -1 && getBalanceFactor(retNode.right) > 0){
                retNode.right = rightRotate(retNode.right); //右孩子先进行右旋转
                return leftRotate(retNode);  //自己再进行左旋转
            }
            return retNode;
        }
    }
}