• 二叉排序树相关概念以及性质
  • 在二叉搜索树中添加元素: add()
  • 查看二叉搜索树中是否存在某个元素 : contains()
  • 找出二叉搜索树中的最小值和最小值 :minimum()、maximum()
  • 删除二叉搜索树中的最小结点和最大结点: removeMin()、removeMax()
  • 删除二叉搜索树中的任意结点: remove()
  • 完整测试源代码

一、 二叉排序树相关概念以及性质

二叉查找树（Binary Search Tree），也称二叉搜索树，是指一棵空树或者具有下列性质的二叉树：

  • 任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
  • 任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值
  • 任意节点的左、右子树也分别为二叉查找树；
  • 没有键值相等的节点(一般)。

相关的性质：

  • 二叉查找树相比于其他数据结构的优势在于查找、插入的时间复杂度较低,为O(log n)。
  • 二叉排序树要求所有的项都能排序，要写出一个一般的类，我们需要实现Comparable接口，使得可以使用泛型来比较任意的数据类型。注意这里不是使用equals方法来实现，根据两项相等当且仅当compareTo方法返回0。
    这里给出BSTreeNode 的定义结构类
  1. public class BSTree<E extends Comparable<E>> {
  3.     private class Node{
  4.         public E e;
  5.         public Node left,right;
  7.         public Node(E e, Node left, Node right) {
  8.             this.e = e;
  9.             this.left = left;
  10.             this.right = right;
  11.         }
  13.         public Node(E e) {
  14.             this.e = e;
  15.             left = null;
  16.             right = null;
  17.         }
  18.     }
  20.     private Node root;
  21.     private int size;
  23.     public BSTree() {
  24.         root = null;
  25.         size = 0;
  26.     }
  27.     public int size(){
  28.         return size;
  29.     }
  30.     public boolean isEmpty(){
  31.         return size == 0;
  32.     }
  33. }

二、在二叉搜索树中添加元素: add()

  • 如果根节点为null，就新建一个根节点；
  • 如果要插入的元素比当前访问结点node小，而且node.left == null，就可以插入到node的左孩子那里；
  • 如果要插入的元素比当前访问结点node大，而且node.right == null，就可以插入到node的右孩子那里；
  • 如果要插入的元素比当前访问结点node小，而且node.left != null，就递归的去左子树插入这个值；
  • 如果要插入的元素比当前访问结点node大，而且node.right != null，就递归的去右子树插入这个值；

二叉排序树相关总结 - 图1

  1.     public void add(E e){
  2.         if(root == null){
  3.             root = new Node(e);
  4.             size++;
  5.         }else {
  6.             add(root,e);
  7.         }
  8.     }
  10.     // 向以node为根的二分搜索树中插入元素，递归算法
  11.     private void add(Node node, E e) {
  12.         if(node.e.equals(e))return;
  14.         if(e.compareTo(node.e) < 0 && node.left == null){ //比node.e小
  15.             node.left = new Node(e);
  16.             size++;
  17.             return;
  18.         }else if(e.compareTo(node.e) > 0 && node.right == null){
  19.             node.right = new Node(e);
  20.             size++;
  21.             return;
  22.         }
  24.         if(e.compareTo(node.e) < 0)// e < node.e && node.left != null
  25.             add(node.left,e);
  26.         else     //e > node.e && node.right != null
  27.             add(node.right,e);
  28.     }
  • 更加简单的写法，也就是当我们递归插入的时候，再多递归一层，当递归到空结点的时候，就插入这个结点，注意add(Node node,E e)方法的作用:
  • 向以node为根的二分搜索树中插入元素，返回插入新结点之后二分搜索树的根，我们在递归的时候要得到返回值和上一层的结点进行连接:
  1.     public void add(E e){
  2.         root = add(root,e);
  3.     }
  4.     private Node add(Node node, E e) { /**向以node为根的二分搜索树中插入元素，返回插入新结点之后二分搜索树的根 */
  5.         if(node == null) {//在这里插入
  6.             size++;
  7.             return new Node(e);
  8.         }
  9.         if(e.compareTo(node.e) < 0){
  10.             node.left = add(node.left,e); //node.left是变化的
  11.         }else if(e.compareTo(node.e) > 0){
  12.             node.right = add(node.right,e);
  13.         }
  14.         return node;
  15.     }

三、查看二叉搜索树中是否存在某个元素 : contains()

在二叉搜索树bsTree中查找x的过程为：

  • 若bsTree是空树，则返回false；
  • 若x等于bsTree的根节点的数据域之值，则查找成功；
  • 若x小于bsTree的根节点的数据域之值，则搜索左子树；
  • 否则搜索右子树；

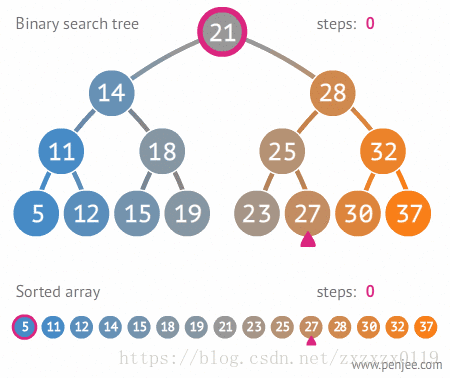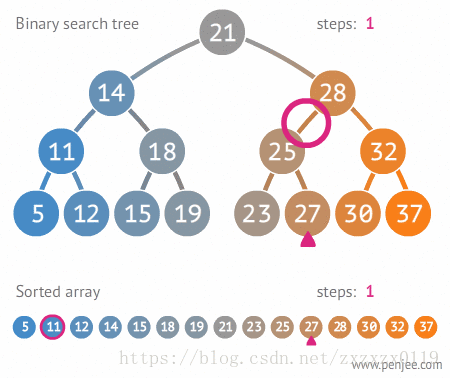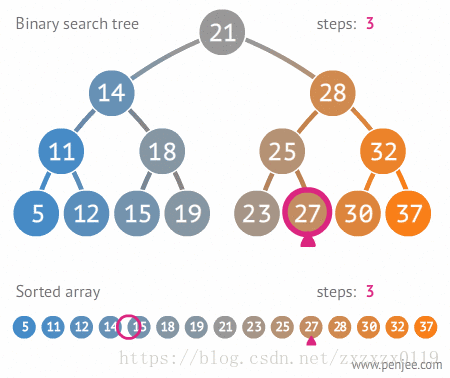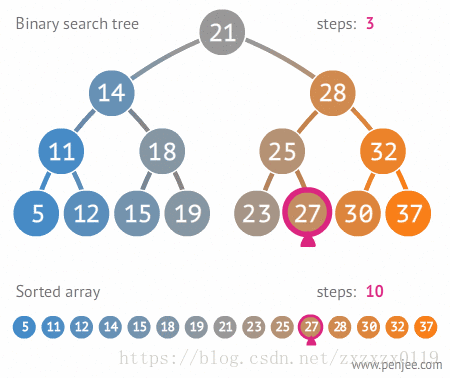
二叉排序树相关总结 - 图2
代码如下：

  1.      //query
  2.     public boolean contains(E e){
  3.         return contains(root,e);
  4.     }
  5.     private boolean contains(Node node, E e) {
  6.         if (node == null) return false;
  7.         if (e.compareTo(node.e) == 0) {
  8.             return true;
  9.         } else if (e.compareTo(node.e) < 0) {
  10.             return contains(node.left, e);
  11.         } else {
  12.             return contains(node.right, e);
  13.         }
  14.     }

四、找出二叉搜索树中的最小值和最小值 : minimum()、maximum()

实现很简单就是一直往左边，或者一直忘右边走，递归和非递归实现都很简单；

  1.     //min
  2.     public E minimum(){
  3.         if(size == 0)
  4.             throw new IllegalArgumentException("BST is empty!");
  5.         return minimum(root).e;
  6.     }
  7.     private Node minimum(Node node) {
  8.         if(node.left == null)return node;
  9.         return minimum(node.left);
  10.     }
  12.     //max
  13.     public E maximum(){
  14.         if(size == 0)
  15.             throw new IllegalArgumentException("BST is empty!");
  16.         return maximum(root).e;
  17.     }
  18.     private Node maximum(Node node){
  19.         if(node.right == null)return node;
  20.         return maximum(node.right);
  21.     }

五、删除二叉搜索树中的最小结点和最大结点: removeMin()、removeMax()

先看删除最小结点：

  • 如果最小结点是叶子结点，很简单直接删除即可；

  • 如果不是叶子结点，就删除这个结点，并且将它的父亲和它的右孩子连接起来即可，看下图:

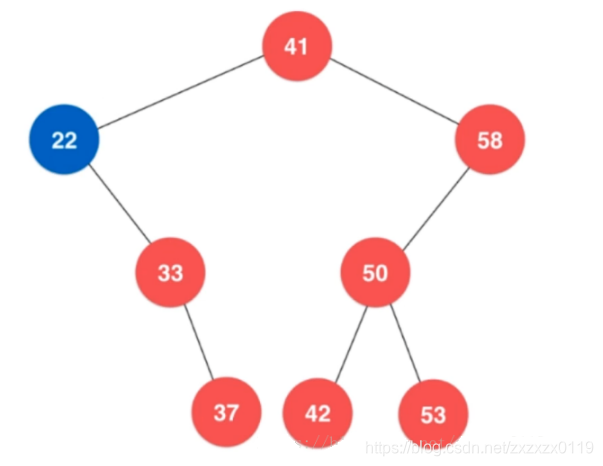
二叉排序树相关总结 - 图3

删除之后就是下面的样子:

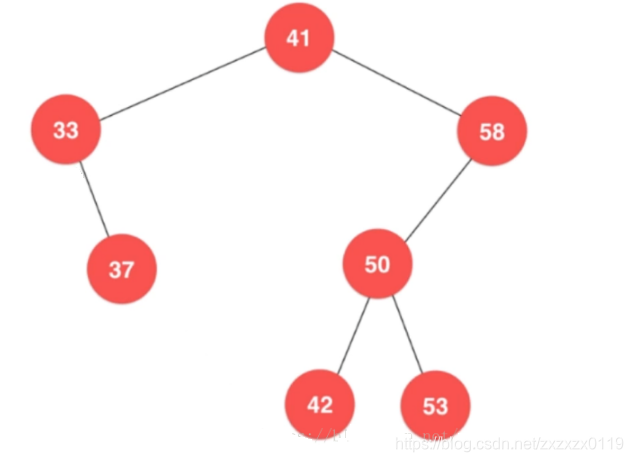
二叉排序树相关总结 - 图4

注意这里的连接就是按照返回值的形式，父亲的左孩子连接上删除之后的树的根即可。

  1.     // 删除二叉搜索树中最小值所在的结点,返回最小值
  2.     public E removeMin(){
  3.         E ret = minimum();
  4.         root = removeMin(root); //remove the min node and then connect the tree
  5.         return ret;
  6.     }
  7.     private Node removeMin(Node node){/**删除掉以node为根的二叉搜索树中的最小结点,返回删除节点后新的结点的二分搜索树的根  */
  8.         if(node.left == null){ //node is min
  9.             Node rightNode = node.right;
  10.             node.right = null; //remove from the tree
  11.             size--;
  12.             return rightNode; /** 返回删除节点后新的结点的二分搜索树的根  然后上一层就可以连接上*/
  13.         }
  14.         node.left = removeMin(node.left); /** 去删除左子树, 然后我要连上你删除之后返回的新的根*/
  15.         return node; /** 返回删除之后的根 ，上一层还要连接*/
  16.     }

删除最大结点同理:

  1.     public E removeMax(){
  2.         E ret = maximum();
  3.         root = removeMax(root);
  4.         return ret;
  5.     }
  6.     private Node removeMax(Node node){
  7.         if(node.right == null){
  8.             Node leftNode = node.left;
  9.             node.left = null;
  10.             size--;
  11.             return leftNode;
  12.         }
  13.         node.right = removeMax(node.right);
  14.         return node;
  15.     }

六、删除二叉搜索树中的任意结点: remove()

删除结点比较复杂，分为四种情况，前三种情况很简单，最后一种情况稍微复杂一点:

  • 如果是叶子结点，直接删除；
  • 如果node只有右孩子，和之前removeMin()的处理一样，删除之后，返回右子树的根节点；
  • 如果node只有左孩子，和之前removeMax()的处理一样，删除之后，返回左子树的根节点；
  • 如果node既有左孩子又有右孩子，就找到node的右子树最小的结点 (后继结点)successor结点，然后用这个结点来顶替node，具体过程和实现看图片和代码；

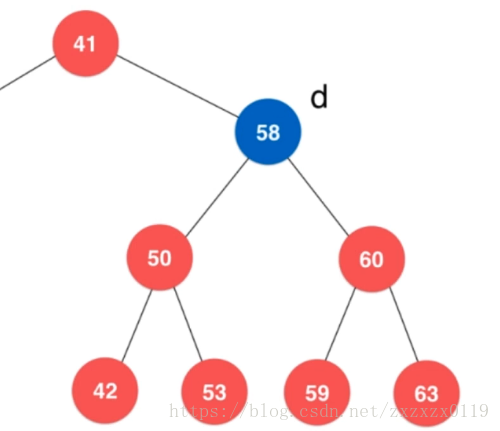
二叉排序树相关总结 - 图5

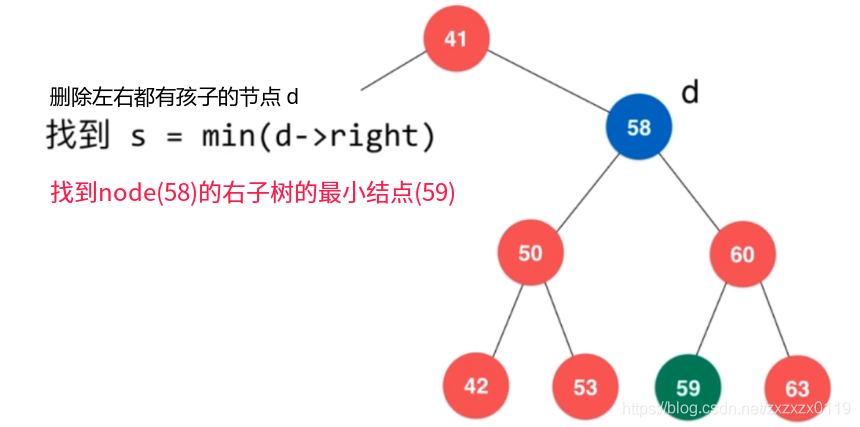
二叉排序树相关总结 - 图6
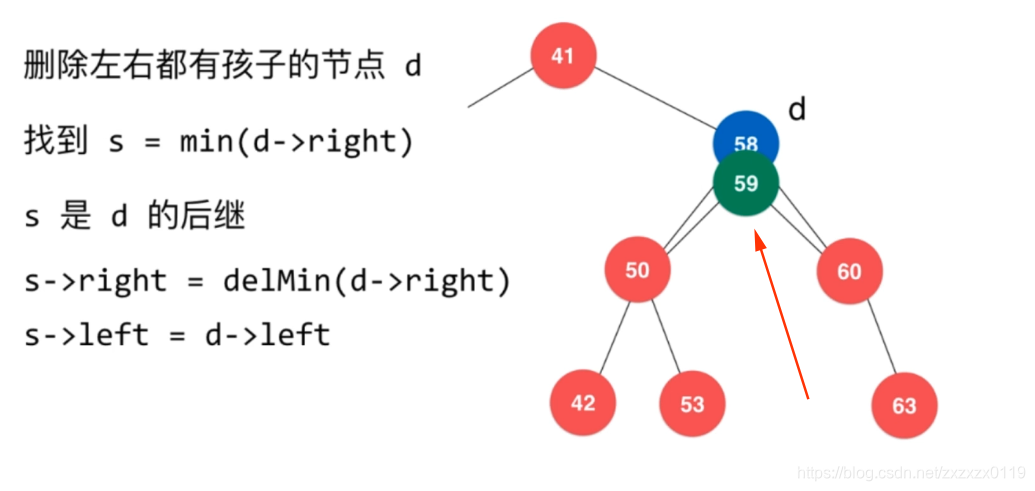
二叉排序树相关总结 - 图7
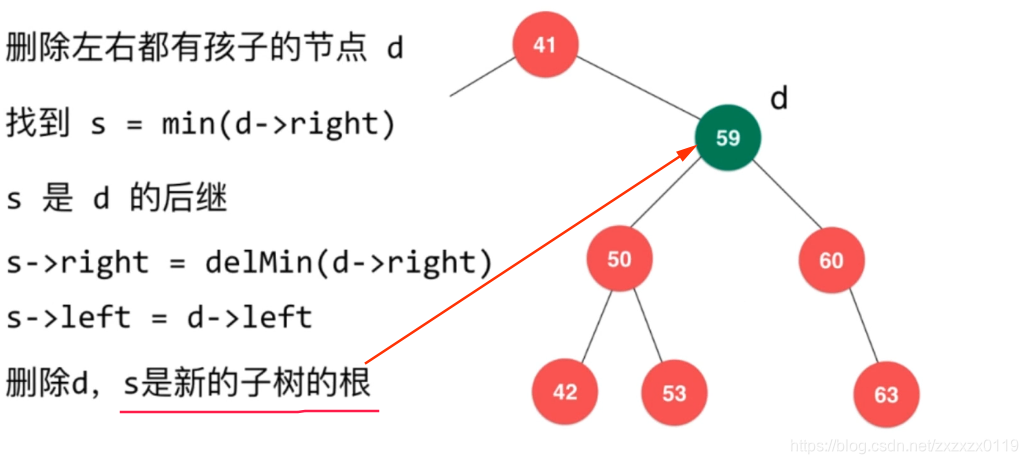
二叉排序树相关总结 - 图8

代码：

  1.     //remove any node
  2.     public void remove(E e){
  3.         root = remove(root,e);
  4.     }
  5.     private Node remove(Node node,E e){/**删除以node为根的二分搜索树中值为e的节点，返回删除节点后新的二叉搜索树的根*/
  6.         if(node == null) return null; // 树中没有这个结点
  7.         if(e.compareTo(node.e) < 0){
  8.             node.left = remove(node.left,e);
  9.             return node;
  10.         }else if(e.compareTo(node.e) > 0){
  11.             node.right = remove(node.right,e);
  12.             return node;
  13.         }else { //e == node.e   ---> should remove
  15.             if(node.left == null){ // only have rightchild or leaf
  16.                 Node rightNode = node.right;
  17.                 node.right = null;
  18.                 size--;
  19.                 return rightNode;
  20.             }
  21.             if(node.right == null){
  22.                 Node leftNode = node.left;
  23.                 node.left = null;
  24.                 size--;
  25.                 return leftNode;
  26.             }
  28.             /** 左右子树都不为空 : 找到比待删除结点大的最小结点(后继)， 用这个结点顶替待删除结点的位置*/
  29.             Node successor = minimum(node.right); //找到右子树的最小结点
  31.             successor.right = removeMin(node.right); //将successor.right设置成 原先结点node的右子树移除 successor之后的树
  32.             successor.left = node.left; //
  34.             //remove node
  35.             node.left = node.right = null;
  36.             //size--;  //这个不需要，因为在removeMin(node.right)中已经减了一次
  37.             return successor; //返回新树的根
  38.         }
  39.     }

还有一个要注意的就是删除之后不需要size--，因为我们在node的右子树中删除那个最小的(successor)结点并顶替node的时候，在removeMin()中已经size- -了，所以不要再减去。

七、完整测试代码

  1. package DataStructure.Tree.BST;
  3. public class BSTree<E extends Comparable<E>> {
  5.     private class Node{
  6.         public E e;
  7.         public Node left,right;
  9.         public Node(E e, Node left, Node right) {
  10.             this.e = e;
  11.             this.left = left;
  12.             this.right = right;
  13.         }
  15.         public Node(E e) {
  16.             this.e = e;
  17.             left = null;
  18.             right = null;
  19.         }
  20.     }
  22.     private Node root;
  23.     private int size;
  25.     public BSTree() {
  26.         root = null;
  27.         size = 0;
  28.     }
  29.     public int size(){
  30.         return size;
  31.     }
  32.     public boolean isEmpty(){
  33.         return size == 0;
  34.     }
  37. /**
  38.     //easy  understand version
  39.     public void add(E e){
  40.         if(root == null){
  41.             root = new Node(e);
  42.             size++;
  43.         }else {
  44.             add(root,e);
  45.         }
  46.     }
  48.     // 向以node为根的二分搜索树中插入元素，递归算法
  49.     private void add(Node node, E e) {
  50.         if(node.e.equals(e))return;
  52.         if(e.compareTo(node.e) < 0 && node.left == null){ //比node.e小
  53.             node.left = new Node(e);
  54.             size++;
  55.             return;
  56.         }else if(e.compareTo(node.e) > 0 && node.right == null){
  57.             node.right = new Node(e);
  58.             size++;
  59.             return;
  60.         }
  62.         if(e.compareTo(node.e) < 0)// e < node.e && node.left != null
  63.             add(node.left,e);
  64.         else     //e > node.e && node.right != null
  65.             add(node.right,e);
  66.     }
  67. */
  68.     //add
  69.     public void add(E e){
  70.         root = add(root,e);
  71.     }
  72.     private Node add(Node node, E e) { /**向以node为根的二分搜索树中插入元素，返回插入新结点之后二分搜索树的根 */
  73.         if(node == null) {//在这里插入
  74.             size++;
  75.             return new Node(e);
  76.         }
  77.         if(e.compareTo(node.e) < 0){
  78.             node.left = add(node.left,e); //node.left是变化的
  79.         }else if(e.compareTo(node.e) > 0){
  80.             node.right = add(node.right,e);
  81.         }
  82.         return node;
  83.     }
  86.     //query
  87.     public boolean contains(E e){
  88.         return contains(root,e);
  89.     }
  90.     private boolean contains(Node node, E e) {
  91.         if (node == null) return false;
  92.         if (e.compareTo(node.e) == 0) {
  93.             return true;
  94.         } else if (e.compareTo(node.e) < 0) {
  95.             return contains(node.left, e);
  96.         } else {
  97.             return contains(node.right, e);
  98.         }
  99.     }
  101.     public E minimum(){
  102.         if(size == 0)
  103.             throw new IllegalArgumentException("BST is empty!");
  104.         return minimum(root).e;
  105.     }
  106.     private Node minimum(Node node) {
  107.         if(node.left == null)return node;
  108.         return minimum(node.left);
  109.     }
  111.     public E maximum(){
  112.         if(size == 0)
  113.             throw new IllegalArgumentException("BST is empty!");
  114.         return maximum(root).e;
  115.     }
  116.     private Node maximum(Node node){
  117.         if(node.right == null)return node;
  118.         return maximum(node.right);
  119.     }
  122.     // 删除二叉搜索树中最小值所在的结点,返回最小值
  123.     public E removeMin(){
  124.         E ret = minimum();
  125.         root = removeMin(root); //remove the min node and then connect the tree
  126.         return ret;
  127.     }
  128.     private Node removeMin(Node node){/**删除掉以node为根的二叉搜索树中的最小结点,返回删除节点后新的结点的二分搜索树的根  */
  129.         if(node.left == null){ //node is min
  130.             Node rightNode = node.right;
  131.             node.right = null; //remove from the tree
  132.             size--;
  133.             return rightNode; /** 返回删除节点后新的结点的二分搜索树的根  然后上一层就可以连接上*/
  134.         }
  135.         node.left = removeMin(node.left); /** 去删除左子树, 然后我要连上你删除之后返回的新的根*/
  136.         return node; /** 返回删除之后的根 ，上一层还要连接*/
  137.     }
  139.     public E removeMax(){
  140.         E ret = maximum();
  141.         root = removeMax(root);
  142.         return ret;
  143.     }
  144.     private Node removeMax(Node node){
  145.         if(node.right == null){
  146.             Node leftNode = node.left;
  147.             node.left = null;
  148.             size--;
  149.             return leftNode;
  150.         }
  151.         node.right = removeMax(node.right);
  152.         return node;
  153.     }
  156.     //remove any node
  157.     public void remove(E e){
  158.         root = remove(root,e);
  159.     }
  160.     private Node remove(Node node,E e){/**删除以node为根的二分搜索树中值为e的节点，返回删除节点后新的二叉搜索树的根*/
  161.         if(node == null) return null; // 树中没有这个结点
  162.         if(e.compareTo(node.e) < 0){
  163.             node.left = remove(node.left,e);
  164.             return node;
  165.         }else if(e.compareTo(node.e) > 0){
  166.             node.right = remove(node.right,e);
  167.             return node;
  168.         }else { //e == node.e   ---> should remove
  170.             if(node.left == null){ // only have rightchild or leaf
  171.                 Node rightNode = node.right;
  172.                 node.right = null;
  173.                 size--;
  174.                 return rightNode;
  175.             }
  176.             if(node.right == null){
  177.                 Node leftNode = node.left;
  178.                 node.left = null;
  179.                 size--;
  180.                 return leftNode;
  181.             }
  183.             /** 左右子树都不为空 : 找到比待删除结点大的最小结点(后继)， 用这个结点顶替待删除结点的位置*/
  184.             Node successor = minimum(node.right); //找到右子树的最小结点
  186.             successor.right = removeMin(node.right); //将successor.right设置成 原先结点node的右子树移除 successor之后的树
  187.             successor.left = node.left; //
  189.             //remove node
  190.             node.left = node.right = null;
  191.             //size--;  //这个不需要，因为在removeMin(node.right)中已经减了一次
  192.             return successor; //返回新树的根
  193.         }
  194.     }
  197.     public void printTree(){
  198.         printTree(root,0,"H",8);
  199.     }
  200.     public void printTree(Node head,int height,String to,int len){
  201.         if(head == null)return;
  202.         printTree(head.right,height + 1,"v",len);
  204.         String val = to + head.e + to;  //两边指示的字符
  205.         int lenV = val.length();
  206.         int lenL = (len - lenV)/2;  //左边的空格(分一半)
  207.         int lenR = len - lenV - lenL; // 右边的空格
  208.         System.out.println( getSpace(len * height) + getSpace(lenL) + val + getSpace(lenR));
  210.         printTree(head.left,height + 1,"^",len);
  211.     }
  212.     public static String getSpace(int len){
  213.         StringBuffer str = new StringBuffer();
  214.         for(int i = 0; i < len; i++) str.append(" ");
  215.         return str.toString();
  216.     }
  220.     public static void main(String[] args) {
  221.         Integer[] arr = {21,14,28,11,18,25,32,5,12,15,19,23,27,30,37};
  222.         //        Arrays.sort(arr); //退化成链表
  223.         BSTree<Integer>bsTree = new BSTree<>();
  224.         for(int i = 0; i < arr.length; i++) bsTree.add(arr[i]);
  225.         bsTree.printTree();
  226.         System.out.println("--------------华丽分割线-------------");
  228.         System.out.println(bsTree.contains(27));
  229.         System.out.println(bsTree.contains(99));
  230.         System.out.println(bsTree.minimum());
  231.         System.out.println(bsTree.maximum());
  232.         System.out.println("--------------华丽分割线-------------");
  234. //        bsTree.removeMin();
  235. //        bsTree.removeMax();
  236. //        bsTree.printTree();
  237.         bsTree.remove(25);
  238.         bsTree.printTree();
  239.     }
  240. }

效果:

二叉排序树相关总结 - 图9

  • 打印二叉树见这个博客。
  • 注意到我在main中测试时注释了Arrays.sort(arr);这一行，因为如果是这样插入的话就会退化成链表，这个进阶的问题就是平衡二叉树。