冒泡排序

冒泡排序是比较简单的排序算法，它的运作过程如下：

进行n-1次排序。
每次排序从0~n-1-i(i是次数编号)，检查这个序列中的数，两两相邻的数，如果前面的大于后面的就将它们交换，这样使得大的数往后面走，每次冒泡就会将一个大的数往后面冒，从而达到目的。

public static void bubbleSort(int[] arr) {
    for (int end = arr.length - 1; end > 0; end--) {
        boolean flag = true;
        for (int i = 0; i < end; i++) {
            if (arr[i] > arr[i + 1]) {
                swap(arr, i, i + 1);
                flag = false;
            }
        }
        if (flag) break;
    }
}

写法2：

 static void swap(int[] arr,int i,int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
    public void bubbleSort(int[] arr) {
        int temp = 0;
        boolean flag = false;
        for (int i = 0; i < arr.length - 1; i++) {
            for (int j = 0; j < arr.length - 1 - i; j++) {
                if (arr[j] > arr[j + 1]) {
                    flag = true;
                    swap(arr,j,j+1);
                }
            }
            //flag=true表示发生排序，false表示没有发生排序
            if (!flag) { //在一趟排序中，一次都没有交换
                break;
            } else {
                flag = false;
            }
        }
    }

我们可以还可以做一个优化 :

记录上一次最后交换的那个位置border；
下一轮交换只需要进行到这个位置即可；

static void bubbleSort2(int[] arr){
    for(int end = arr.length-1; end > 0; end--){
        int border = 0;
        for(int i = 0; i < end; i++){
            if(arr[i] > arr[i+1]){
                swap(arr, i, i+1);
                border = i+1;
            }
        }
        end = border;
    }
}

鸡尾酒排序-改进的冒泡排序

也叫做定向冒泡排序:

它的改进在于同时的冒泡两边，从低到高，然后从高到低；
相当于顺便把最小的数也冒泡到最前面这个方法比冒泡更加高效一点；

代码:

/**改进的冒泡排序(鸡尾酒排序)  就是把最大的数往后面冒泡的同时，　最小的数也往前面冒泡*/
static void cocktailSort(int[] arr) {
    int L = 0,R = arr.length-1;
    while(L < R) {
        for(int i = L; i < R; i++) if(arr[i] > arr[i+1]) swap(arr,i,i+1);
        R--;
        for(int i = R; i > L; i--) if(arr[i] < arr[i-1]) swap(arr,i,i-1);
        L++;
    }
}

快速排序

快速排序有几种不同的实现方式，先看最简单的，快排的宏观过程就是每次递归左右两边划分，关键是划分的过程，即partition过程的写法，先看最原始的partition:

在[L, R]之间，选取arr[L]为划分点key；
然后从[L, R]，如果当前arr[i] < key，就放到左边部分swap(arr, i, ++pivot);，否则就不动；
最后将数组划分成了arr[L...p-1] < arr[p] ， arr[p+1...R] > arr[p]，并返回p；

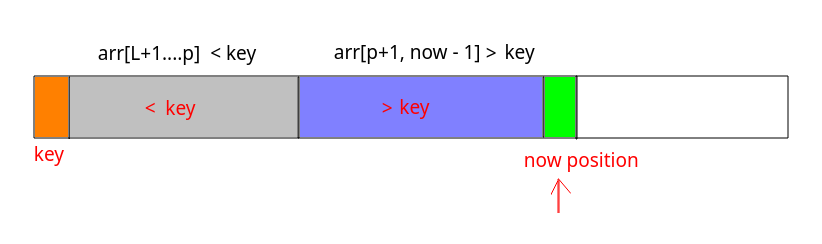
代码:

static void quickSort(int arr[]) {
    if (arr == null || arr.length <= 1)
        return;
    quickProcess(arr, 0, arr.length - 1);
}
static void quickProcess(int[] arr, int L, int R) {
    if (L >= R)
        return;
    int p = partition(arr, L, R);
    quickProcess(arr, L, p - 1);
    quickProcess(arr, p + 1, R);
}
/**
* 对arr[l...r]部分进行partition操作
* 返回p, 使得arr[L...p-1] < arr[p] ; arr[p+1...R] > arr[p]
*/
static int partition(int[] arr, int L, int R) {
    //直接选取 arr[L]作为pivot(中心点)
    int key = arr[L];
    int pivot = L;
    for (int i = L + 1; i <= R; i++) {
        if (arr[i] < key)
            swap(arr, i, ++pivot);
    }
    swap(arr, pivot, L); // 将arr[L]放到pivot位置(中间) --> 完全了按照arr[L]划分数组的目的
    return pivot;
}

第一个优化(随机快排) (解决划分数选取不好的问题)
上面的快速排序当选取的划分的元素(pivot = arr[L])很小(或者很大)，使得后面划分的数组极度的不平衡的时候，会将快速排序降到O(N)，于是我们使用随机快排，即不是将arr[L]作为划分点，而是随机选取一个元素作为(pivot)：

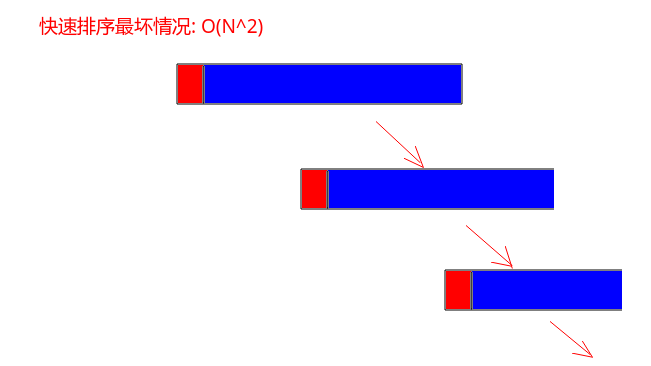
代码:

static void quickProcess(int[] arr, int L, int R) {
    if (L >= R) return;
    swap(arr, L, L + (int) (Math.random() * (R - L + 1))); //随机选取一个pivot
    int p = partition(arr, L, R);
    quickProcess(arr, L, p - 1);
    quickProcess(arr, p + 1, R);
}

第二个优化(双路快速排序)(解决重复元素多的问题)

当我们要排序的数组重复元素很多的情况下，还是会使得划分极其的不均匀:

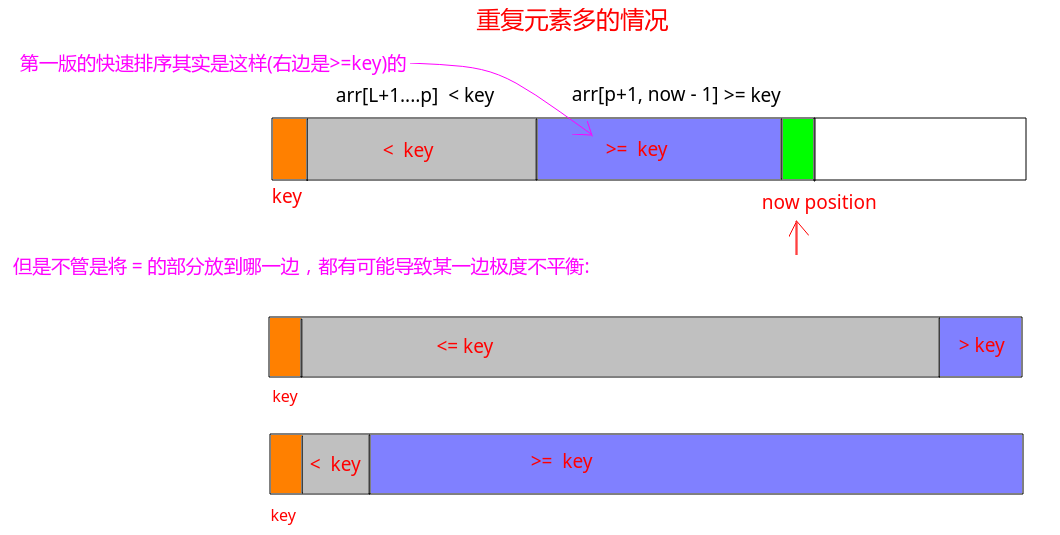
第一个解决的方法: 换一种划分的方式:

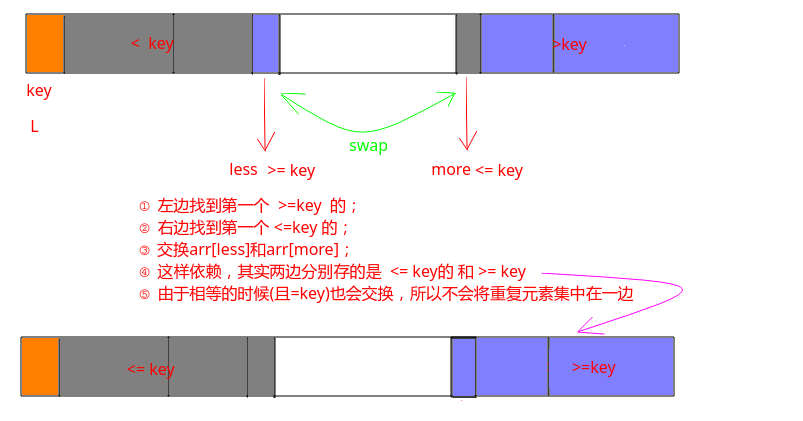
将 <key和>key的元素放在数组的两边，更准确的说是: 左端放的是 <=key的元素，右端放的是>=key的元素；
然后设置两个指针(一个从L开始，一个从R开始)，然后向中间靠拢，分别找到第一个>=key(左边)、<=key(右边)的元素，就停止扫描，然后交换这两个位置，终止条件是两个指针相碰；
为什么这样就可以解决重复元素多的问题呢? 因为两个指针的元素相等且都等于key的时候，还是要交换两个位置，这样就不会将重复的元素集中在同一侧。

解决方式:

改进代码:

static void quickSort(int arr[]) {
    if (arr == null || arr.length <= 1)
        return;
    quickProcess(arr, 0, arr.length - 1);
}
static void quickProcess(int[] arr, int L, int R) {
    if (L >= R)
        return;
    swap(arr, L, L + (int) (Math.random() * (R - L + 1))); //随机选取一个pivot
    int p = partition(arr, L, R);
    quickProcess(arr, L, p - 1);
    quickProcess(arr, p + 1, R);
}
static int partition(int[] arr, int L, int R) {
    int key = arr[L];
    int less = L + 1, more = R;
    while (true) {
        while (less < R && arr[less] < key) less++;
        while (more > L && arr[more] > key) more--;
        if (less >= more)// not less > more  
            break;
        swap(arr, less++, more--);
    }
    swap(arr, L, more); // finally let L to the middle 
    return more;
}

第三个优化(三路快速排序)(更好的解决重复元素多的问题)
三路快排关键在于partion的过程(荷兰国旗问题)，也就是将一个数组按照某个数划分成三部分:

先从序列中选取一个数作为基数(key)；
分区过程，将<key放到左边，>key的放在右边，=key放到中间；
再对左右区间重复第二步，直到各区间只有一个数；
返回的p数组中p[0]代表的是等于区域的左边界，p[1]代表的是等于区域的右边界；

过程: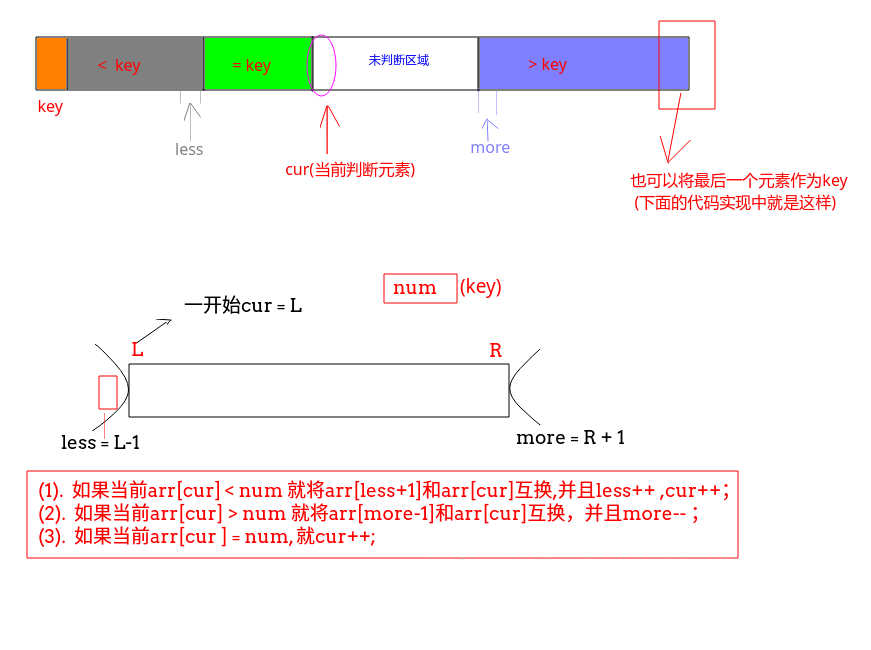

代码:

static int[] partition(int[] arr, int L, int R, int num) {
    int less = L - 1; //小于部分的最后一个数
    int more = R + 1;
    int cur = L;
    while (cur < more) {
        if (arr[cur] < num) {
            swap(arr, ++less, cur++); //把这个比num小的数放到小于区域的下一个，并且把小于区域扩大一个单位
        } else if (arr[cur] > num) {
            swap(arr, --more, cur); //把这个比num大的数放到大于去余的下一个，并且把大于区域扩大一个单位
            //同时，因为从大于区域拿过来的数是未知的，所以不能cur++ 还要再次判断一下arr[cur]
        } else {// 否则的话就直接移动
            cur++;
        }
    }
    return new int[]{less + 1, more - 1};  //返回的是等于区域的两个下标
}

荷兰国旗问题的一个经典应用题LeetCode75-Sort Colors。
注意这里的快速排序就是partition更改的，默认将R中的最后一个作为划分(也可以用arr[L])．
这里总结一下优化 (所有的优化都是为了划分的均匀):

这里实际上使用的是三路快排，这个是为了防止数组中有很多重复的元素；
使用的是随机快排，时间复杂度是概率级别的Ologn(防止数组近乎有序)；
注意下面我写了四种partition的过程，达到的效果是一样的，分别使用arr[L]和arr[R]来作划分，一些细节和边界的不同导致程序不同；

最终三路快排代码如下: (下面的四个partition都是三路快排，只不过写的稍微有点不同)

static void quickSort(int arr[]) {
    if (arr == null || arr.length <= 1) return;
    quickProcess(arr, 0, arr.length - 1);
}
/**
 * 使用随机快排 (也就是 时间复杂度是概率的，防止我们选取的划分的数使得左右两边划分的很不均匀)
 * 随机快排的额外空间复杂度为Ologn
 */
static void quickProcess(int[] arr, int L, int R) {
    if (L >= R)
        return;
    /**随机化的排序 期望为Ologn从前面的数中随机选出一个数和最后一个数交换 不至于极端的情况使得两边划分很不对称*/
    swap(arr, R, L + (int) (Math.random() * (R - L + 1))); //例子3~6 --> [0~1)*3 --> 0~2
    int[] p = partition4(arr, L, R); // 分别用partition、partition2、partition3测试都可以
    quickProcess(arr, L, p[0] - 1);
    quickProcess(arr, p[1] + 1, R);
}
/**
 * 划分函数,这里使用的是arr[R]来划分, 左边的都比arr[R]小，右边都比arr[R]大
 * 返回的数组是中间相等的两个下标
 */
static int[] partition(int[] arr, int L, int R) {
    int cur = L, less = L - 1, more = R;
    int key = arr[R];
    while (cur < more) {
        if (arr[cur] < key)
            swap(arr, ++less, cur++);
        else if (arr[cur] > key)
            swap(arr, --more, cur);
        else
            cur++;
    }
    swap(arr, more, R);  //把最后那个数放到中间
    return new int[]{less + 1, more};  //当然如果没有相等的部分  那less+1 = more
}
/**
 * 上面的简写方式
 **/
static int[] partition2(int[] arr, int L, int R) {
    int less = L - 1, more = R;  //把最后这个数当作标准 也可以使用第一个
    while (L < more) {
        if (arr[L] < arr[R])
            swap(arr, ++less, L++);
        else if (arr[L] > arr[R])
            swap(arr, --more, L);
        else
            L++;
    }
    swap(arr, more, R);  //把最后那个数放到中间
    return new int[]{less + 1, more};  //为什么不是 more-1,因为上面又交换了一个, 当然如果没有相等的部分  那less+1 = more
}
/**
 * 正方向：按照 arr[L]来划分
 **/
static int[] partition3(int[] arr, int L, int R) {
    int key = arr[L], cur = L + 1;
    int less = L, more = R + 1; // more在外面(R+1)，等下循环cur < more
    while (cur < more) {
        if (arr[cur] < key)
            swap(arr, ++less, cur++);
        else if (arr[cur] > key)
            swap(arr, --more, cur);
        else cur++;
    }
    swap(arr, L, less);
    return new int[]{less, more - 1};
}
/**
 * 对比partition3的不同
 **/
static int[] partition4(int[] arr, int L, int R) {
    int key = arr[L], cur = L + 1;
    int less = L, more = R; // more = R，等下循环cur <= more
    while (cur <= more) { // not cur < more
        if (arr[cur] < key)
            swap(arr, ++less, cur++);
        else if (arr[cur] > key)
            swap(arr, more--, cur); // 对比上面,不是--more,这些就是边界问题
        else cur++;
    }
    swap(arr, L, less);
    return new int[]{less, more}; //同样返回的也不同
}
static void swap(int[] arr, int a, int b) {
    int temp = arr[a];
    arr[a] = arr[b];
    arr[b] = temp;
}

注意这里和荷兰国旗partitiion过程的不同:

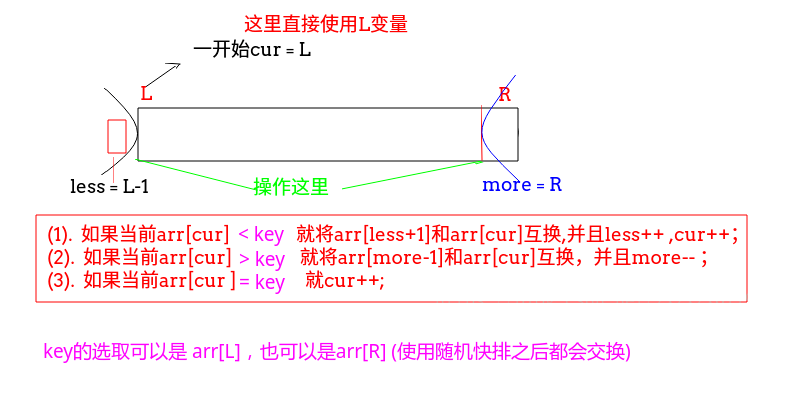
注意最后的arr[more]和arr[R]的交换(注意最后的交换和返回的下标位置):

数据结构

交换排序

冒泡排序

鸡尾酒排序-改进的冒泡排序

快速排序