什么是自由度
自由度全称 Degrees of Freedom,简称 DoF 。
自由度是用最少的数据配置来描述物体在空间中位置或形态。
空间位置描述
一维空间的点

在一维空间的线段中,我们来描述一个点,我们通常用一个数字描述。
例如上图:
- 我们描述蓝色的点的位置用 1 可以准确的表达。
在一维空间的线段中,我们来描述一个点,我们通常用一个数字描述。
例如上图:
-
二维空间的单点

在二维空间中,我们描述一个点,我们通常用横纵坐标来进行描述。
如上图: -
二维空间的两点
如果我们要描述两个点,如下图:
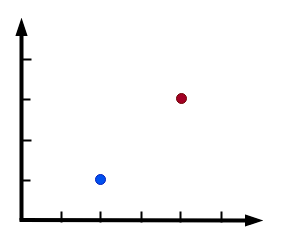
我们要描述蓝色的点和红色的点,那么我们可以用连个坐标点来进行描述: -
二维空间中的线段
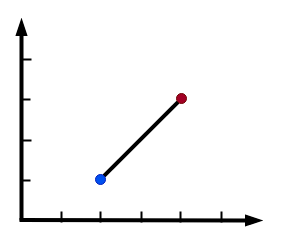
在二维空间中,我们如果要去描述一个线段,该如何去准确表达呢。
我们可以: 描述起始点和结束点,起始点(2,1) 结束点(4, 3)
Note
我们所有的数学问题都是为了解决现实生活的。
我们如果将线段看成一条棍子,如何在一个桌子上去描述棍子的位置呢?
认识自由度
二维空间中的棍子

我们将桌子看成一个坐标系,那么我们如果用大白话去描述棍子的位置,我们会说:
棍子斜着朝上摆在靠上的地方。
这种描述并不准确,但是说明了两个问题:
- 斜着朝上 说明的是角度
- 靠上说明的是位置
如果我们准确的去表达:
棍子起始坐标点为 (2,1) 的位置,角度是45度
Note
这里值得思考的是,描述以上问题时,是有前置条件的:
- 棍子的长度是确定的。
- 角度起始位置问题。
- 角度旋转的正负方向问题。
- 坐标系如何摆放问题。
角度起始:我们将x轴正向定义为角度起始点。
角度旋转正负:逆时针定义为正向,顺时针定义为负向。
坐标系摆放:坐标系其实可以随意摆放,摆放不同,位置描述就不同。
棍子的思考
棍子是摆放在桌子上的,那么我们是不是可以随时改变棍子的位置呢?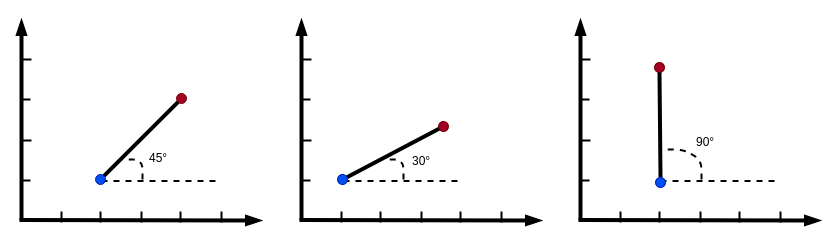
通过上图,我们可以得出一个结论:
- 可以控制棍子的平移位置
- 可以控制棍子的旋转姿态
哪什么是自由度呢?
对于棍子来说,可以水平垂直移动,可以旋转,这个就是自由,这个就是自由度。
准确的说,自由度表现在位移和旋转的能力上。
对于当前的状况而言,棍子和桌子构成了一个系统,这个系统中,棍子具备了一定的自由度。这个自由度表现在,可以水平移动,可以垂直移动,可以旋转。那么我们可以说棍子具备3个自由度。
Note
小结:
在二维空间中,自由度体现在 水平移动,垂直移动,旋转三个方面。
通常我们会说某某物体有几个自由度,说的就是他是否具备移动和旋转方面的自由度。
思考:
如果是三维空间,那么自由度主要是指那几个方面?
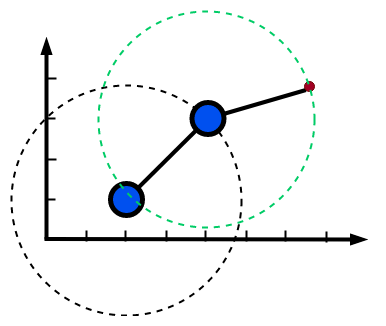
固定的连杆

如上图,在二维的空间中,现在存在一个连杆,其中蓝色的一端是固定在桌子上的。那么对于这个连杆而言,他具备几个自由度呢?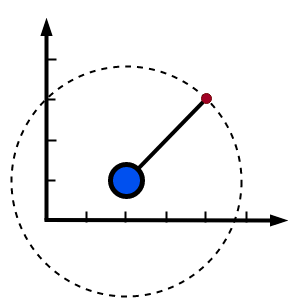
由于一端已经固定,整个木棍是不可以再移动了,只能围绕着这个固定的点进行旋转,因此只有旋转方面的自由度。
自由度描述
单连杆固定系统
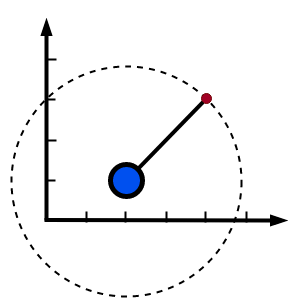
对于这个连杆来说,自由度我们已经确定,只有一个可以旋转的自由度。那么我们如何准确的描述这个连杆的位置呢?
通常,我们描述起始位置(蓝色点)的坐标,以及旋转的角度,就可以准确的描述出这个连杆的位置和姿态。
双连杆系统
关节类型和自由度