描述性统计

1、平均数

反映数据集中趋势的一项指标，主要类型有算数平均数、几何平均数、加权平均数。

1.1算数平均数公式

1.2几何平均数公式：

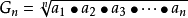
1.3加权平均数公式：

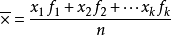，其中 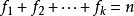， f、f、…、f叫做权(weight)

2、众数

反映了一组数据的集中程度

3、中位数

反映数据的中心位置的指标

4、最大（小）数

一组数据中最大（小）的那个数

5、四分位数

描述数据的整体分布状况。
基于N-1基础，
Q1的位置=1+（n-1）x 0.25
Q2的位置=1+（n-1）x 0.5
Q3的位置=1+（n-1）x 0.75

案例：
7, 15, 36, 39, 40, 41
1、将数据从小到大排序，计为数组a（1 to n），n代表数据的长度
2、确定四分位数的位置：b= 1+(n-1) × 0.25= 2.25，b的整数部分计为c，b的小数部分计为d
计算Q1：
Q1=a(c)+[a(c+1)-a(c)]d
=a(2)+[a(3)-a(2)] 0.25
=15+（36-15）×0.25=20.25
计算Q2：
b=1+(n-1) ×0.5=3.5

Q2=a(c)+[a(c+1)-a(c)]d
=a(3)+[a(4)-a(3)] 0.5
=36+（39-36）×0.5=37.5
计算Q3：
b=1+(n-1) ×0.75=4.75
Q3=a(c)+[a(c+1)-a(c)]d
=a(4)+[a(5)-a(4)] 0.75
=39+（40-39）*0.75=39.75
3、四分位距（IQR）=Q3-Q1
应用：
1、不同类别数据的比较（箱线图）
2、识别出可能的异常值
最小估计值：Q1-K（Q3-Q1）
最大估计值：Q3-K（Q3-Q1）
K=1.5 中度异常
K=3 极度异常

6、标准差

反映一个数据集的离散程度。
方差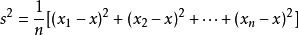：，其中，x表示样本的平均数，n表示样本的数量，xi表示个体，而s^2就表示方差
方差的算术平方根即标准差

7、标准分数

z=(x-μ)/σ；其中z为标准分数；x为某一具体分数，μ为平均数，σ为标准差
距离平均值多少个标准差