安装分析工具库
文件<选项应用：数据<数据分析

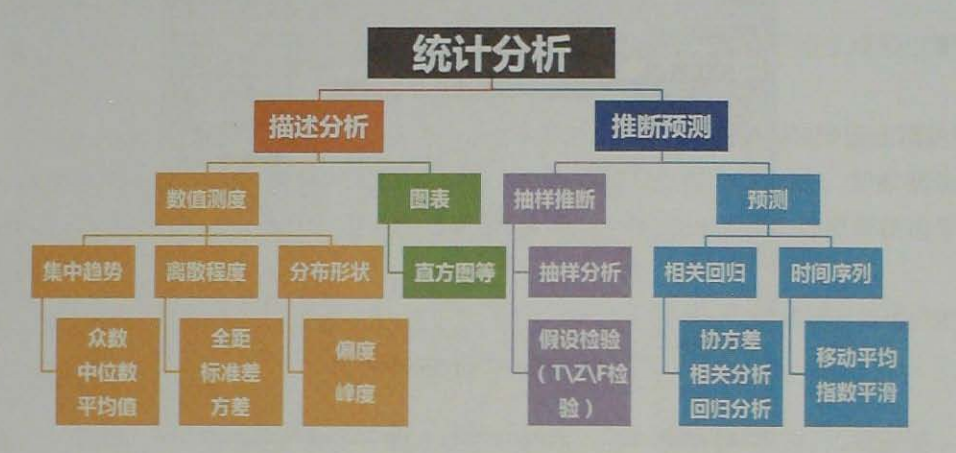
image.png

1.描述性统计分析

操作：excel<数据<数据分析<描述统计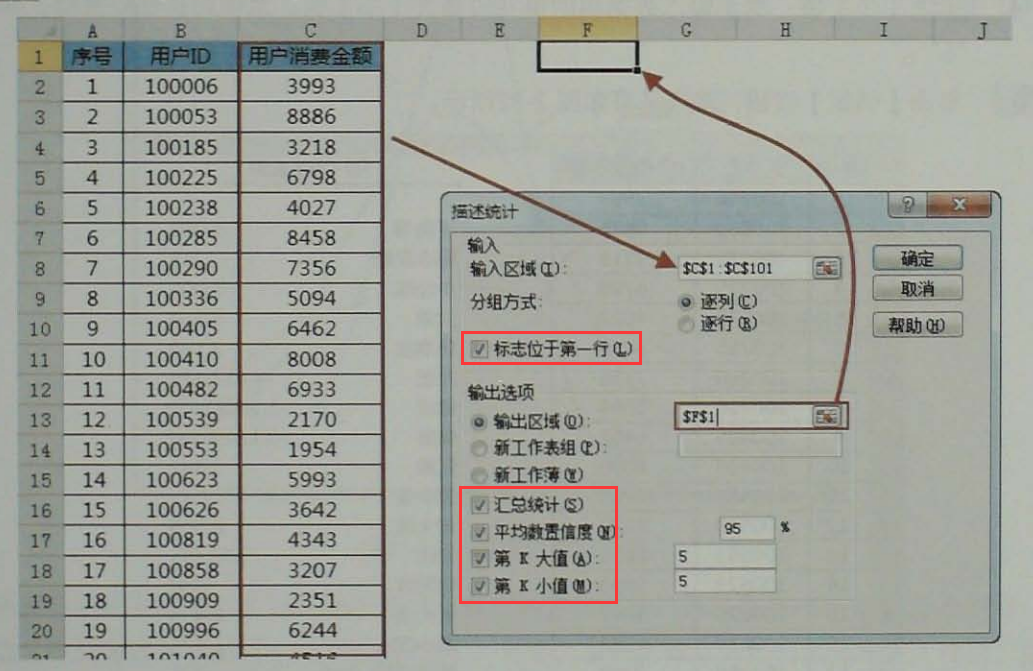
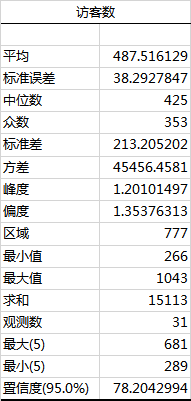
image.png image.png

语雀内容

1.1峰度

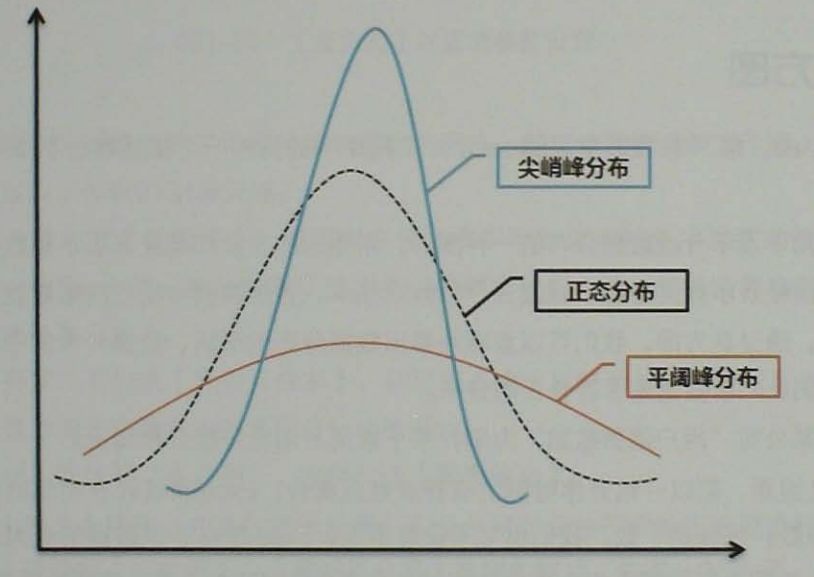
峰度系数是描述对称分布曲线峰顶尖峭程度的指标，是相对于正态分布而言的。

  • 峰度系数>0，两侧极端数据较少，比正态分布更高更瘦，呈尖峭峰分布；
  • 峰度系数<0，表示两侧极端数据较多，比正态分布更矮更胖，呈平阔峰分布。

image.png

1.2偏度

偏度系数是以正态分布为标准来描述数据对称性的指标。
偏度系数=0，就是分布对称；
如果频数分布的高峰向左偏移（偏度系数<0），长尾向右侧延伸称为正偏态分布；
如果频数分布的高峰向右偏移（偏度系数>0），长尾向左延伸则成为负偏态分布。
偏度系数大于1或小于-1，被称为高度偏态分布；
偏度系数在0.5~1或-0.5~-1范围内，被认为是中等偏态分布；
偏度系数越接近0，偏斜程度就越低。
image.png

2.直方图

操作：excel<数据<数据分析<直方图
直方图是用于展示分组数据分布的一种图形，用矩形的宽度和高度来表示频数分布，在直角坐标系中，用横轴表示数据分组，纵轴表示频数或频率，各组数据与相应的频数就形成了一个矩形，即直方图。通过直方图，我们可以直观地看出数据分布的形状、数据分布的中心位置及数据分散的程度，由此判断数据是否符合正态分布。
柏拉图：帕累托图，按降序排列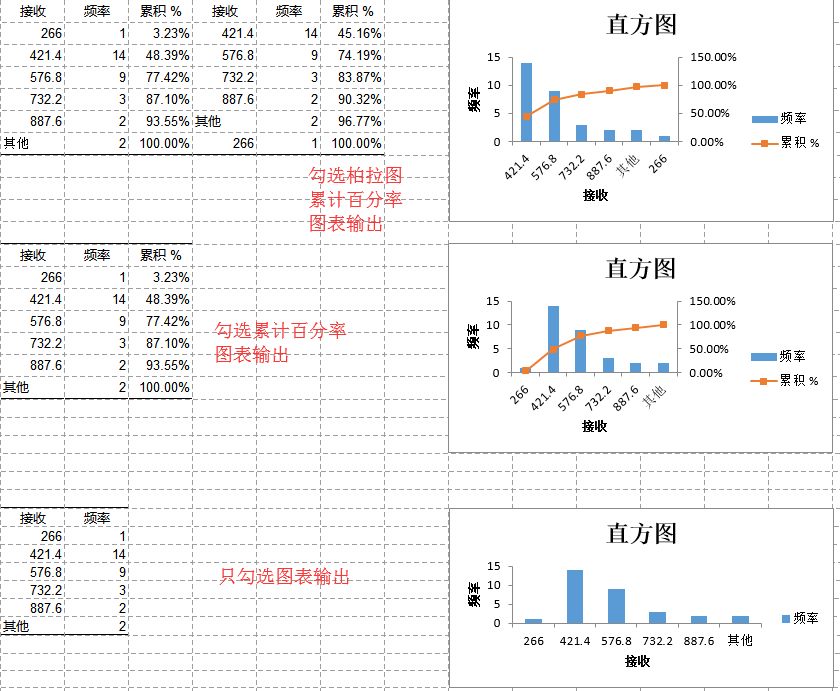
image.png

3.抽样分析

Rand函数只能解决随机抽取，无法解决有规律抽取，这里采用【抽样】分析工具
抽样方法

  • 周期，间隔
  • 随机，样本数

其中随机抽样采用有放回的方式进行随机抽样

4.相关回归预测

4.1相关分析

相关关系
相关关系是指现象之间存在的非严格的、不确定的依存关系。这种依存关系的特点是：某一现象在数量上发生的变化会影响另一现象数量上的变化，而且这种变化具有一定的随机性，即当给定某一现象以一个数值时，另一现象会有若干个数值与之对应，并且总是遵循一定规律，围绕这些数值的平均数上下波动，其原因是影响现象发生变化的因素不止一个。例如，影响销售额的因素除了推广费用外，还有产品质量、价格、渠道等因素。
相关分析是研究两个或两个以上随机变量之间相互依存关系的方向和密切程度的方法。
直线相关用相关系数表示，曲线相关用相关指数表示，多重相关用复相关系数表示，其中我们常用的是直线相关，所以主要研究相关系数。
相关系数就是反映变量之间线性相关强度的一个度量指标，通常用r表示，它的取值范围为[-1，1]。r的正、负号可以反映相关的方向，当r>0时表示线性正相关，当r<0时表示线性负相关；r的大小可以反映相关的程度，r=0表示两个变量之间不存在线性关系。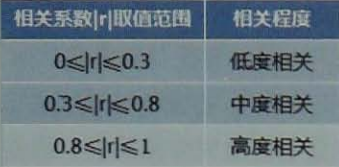
image.png

4.2回归分析

回归函数关系
回归函数关系是指现象之间存在的依存关系中，对于某一变量的每一个数值，都有另一变量值与之相对应，并且这种依存关系可用一个数学表达式反映出来，例如，在一定的条件下，身高与体重存在的依存关系。

4.2.1回归分析模型

线性回归

  • 简单线性回归
  • 多重线性回归

非线性回归
通过对数转化等方式，将非线性回归转化为线性回归的形式进行研究

4.2.2线性回归分析步骤

image.png

4.2.3简单线性回归

又称一元线性回归，即回归模型中只含有一个自变量
image.png
确定自变量和因变量
绘制散点图，显示公式以及显示R平方值
【回归分析】分析工具
回归统计表：拟合优度检验（R）
方差分析表：显著性检验（F检验）又叫P值
回归系数表：显著性检验（t检验）

4.2.4多重线性回归

多重线性回归是指包含一个因变量和多个自变量的回归模型
image.png
多元线性回归是指包含两个或两个以上因变量的回归模型

5.时间序列预测

特点：

  • 假设事物发展趋势会延伸到未来
  • 预测所依据的数据具有不规则性
  • 不考虑事物发展之间的因果关系

    5.1移动平均

    移动期数少，能快速地反映变化，但不能反映变化趋势
    移动期数多，能反映变化趋势，但预测值带有明显的滞后偏差
    移动平均法的基本思想是：移动平均可以消除或减少时间序列数据受偶然性因素干扰而产生的随机变动影响，它适合短期预测，适合短期预测。
    主要包括一次移动平均法，二次移动平均法，加权移动平均法
    image.png
    二次移动平均法式建立在一次移动平均法的基础上，利用一次移动平均法得出的预测结果再进行一次移动平均

    5.2指数平滑

    指数平滑法是从移动平均法发展而来的，是一种改良的加权平均法，在不舍弃历史数据的前提下，对离预测期较近的历史数据给予较大的权数，权数由近到远按指数规律递减。
    指数平滑法根据本期的实际值和预测值，并借助于平滑系数（α）进行加权平均计算，预测下一期的值。它是对时间序列数据给予加权平滑，从而获得其变化规律与趋势。
    Excel中的指数平滑法需要使用阻尼系数（β），阻尼系数越小，近期实际值对预测结果的影响越大；反之，阻尼系数越大，近期实际值对预测结果的影响越小。
    α——平滑系数（0≤α≤1）
    β——阻尼系数（0≤β≤1），β=1-α
    在实际应用中，阻尼系数是根据时间序列的变化特性来选取的。
    若时间序列数据的波动不大，比较平稳，则阻尼系数应取小一些，如0.1~0.3。
    若时间序列数据具有迅速且明显的变动倾向，则阻尼系数应取大一些，如0.6~0.9。
    image.png
    指数平滑法可以分为一次指数平滑法、二次指数平滑法及三次指数平滑法。

    5.3趋势外推

    5.4季节变动