面试题10-easy 斐波那契数列及青蛙跳问题

面试题10- I. 斐波那契数列

写一个函数，输入 n ，求斐波那契（Fibonacci）数列的第 n 项。斐波那契数列的定义如下：
F(0) = 0,   F(1) = 1
F(N) = F(N - 1) + F(N - 2), 其中 N > 1.
斐波那契数列由 0 和 1 开始，之后的斐波那契数就是由之前的两数相加而得出。
答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。
示例 1：
输入：n = 2
输出：1
示例 2：
输入：n = 5
输出：5
提示：
0 <= n <= 100
注意：本题与主站 509 题相同：https://leetcode-cn.com/problems/fibonacci-number/

一般情况下求斐波那契数列最简单的就是使用递归的方法，但是这样的方法有一个明显的缺点：
超时/栈溢出

如下代码，当n=43时在leetcode上显示时间超出限制，运行不通过

func fib(n int) int {
    if n<=1{
        return n
    }
    return fib(n-1)+fib(n-2)
}

因此我们使用动态规划来解决这个问题：（其实也是非常简单的）

func fib(n int) int {
    if n<=1{
        return n
    }
    fib_one := 0
    fib_two := 1
    fib_n :=0
    for i:=2;i<=n;i++{
        fib_n = (fib_one + fib_two)% 1000000007
        fib_one = fib_two
        fib_two = fib_n
    }
    return fib_n 
}

一种比较简单的写法：

func fib(n int) int {
    a,b := 0,1
    for i:=0;i<n;i++{
        a,b  = b%1000000007,(a+b)%1000000007
    }
    return a
}

面试题10- II. 青蛙跳台阶问题

一只青蛙一次可以跳上1级台阶，也可以跳上2级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。

答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。

示例 1：

输入：n = 2
输出：2
示例 2：

输入：n = 7
输出：21
提示：

0 <= n <= 100
注意：本题与主站 70 题相同：https://leetcode-cn.com/problems/climbing-stairs/

大佬的解题思路：链接地址

简单理解：不用想青蛙一开始是怎样跳的，只要知道青蛙最后是怎样跳的即可。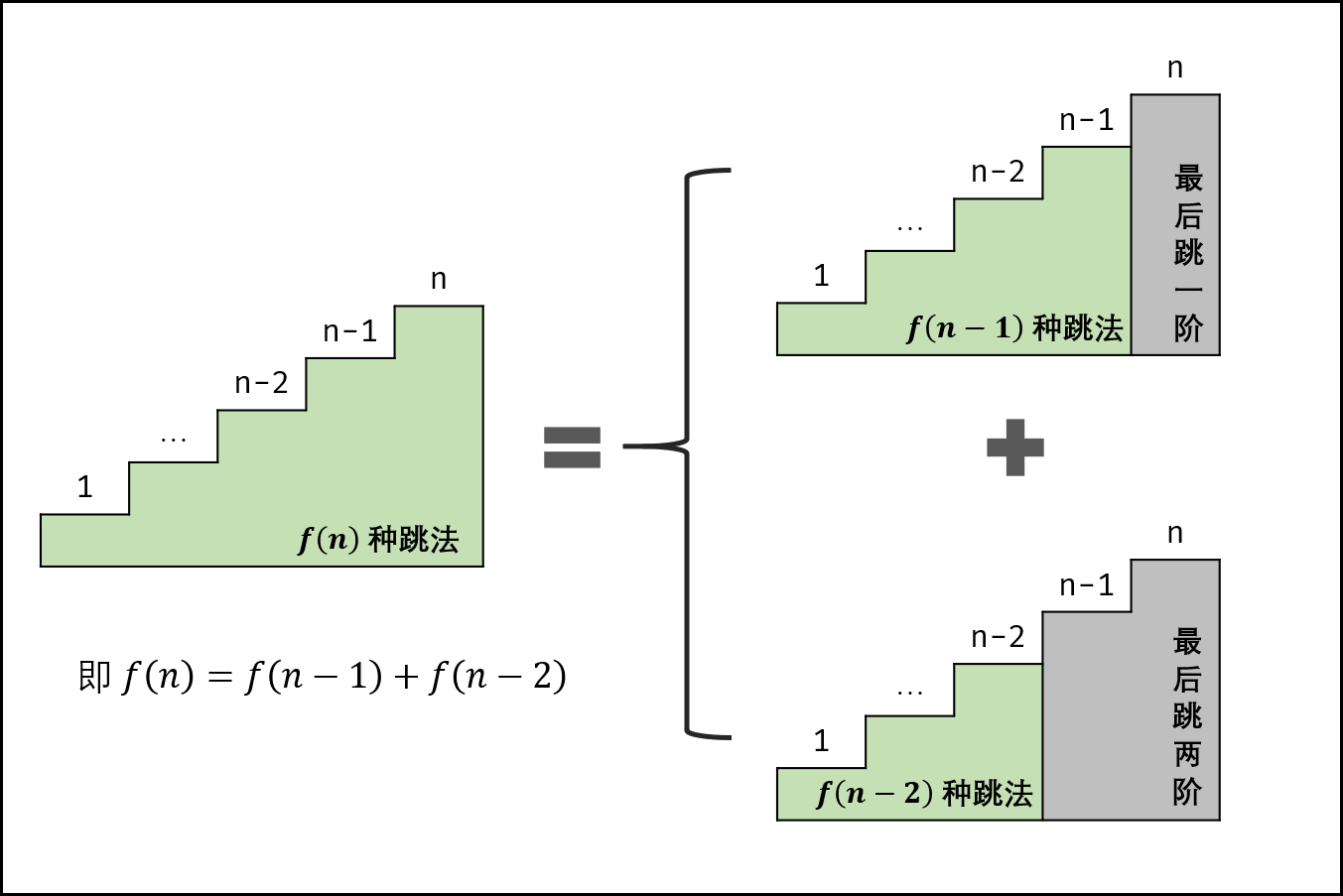

动态规划解析：

状态定义： 设 dp为一维数组，其中 dp[i] 的值代表 斐波那契数列第 $i$ 个数字 。
转移方程： dp[i + 1] = dp[i] + dp[i - 1]，即对应数列定义 f(n + 1) = f(n) + f(n - 1) ；
初始状态： dp[0] = 1, dp[1] = 1 ，即初始化前两个数字；
返回值： dp[n] ，即斐波那契数列的第 n 个数字。
空间复杂度优化：

若新建长度为 n 的 dp列表，则空间复杂度为 O(N) 。

由于 dp列表第 i 项只与第 i-1 和第 i-2项有关，因此只需要初始化三个整形变量 sum, a, b ，利用辅助变量 sumsum 使 a, b 两数字交替前进即可 （具体实现见代码） 。
因为节省了 dp列表空间，因此空间复杂度降至 O(1) 。

利用golang的平行赋值，可以避免使用sum第三变量

func numWays(n int) int {
    a,b :=1,1
    for i:=0;i<n;i++{
        a,b = b % 1000000007, (a+b)% 1000000007
    }
    return a 
}