败者树算法

外部排序时间开销=读写外存的时间+内部排序所需时间+内部归并所需 时间
归并趟数S=⌈logkr⌉

归并路数k增加，归并趟数S减少，读写磁盘总次数减少

使用k路平衡归并策略，选出一个最小元素需要对比关键字（k-1）次， 导致内部归并所需时间增加，因此可以使用败者树进行优化，减小比较次数

8路平衡归并，从八个归并段中选出一个最小元素需要对比关键字7次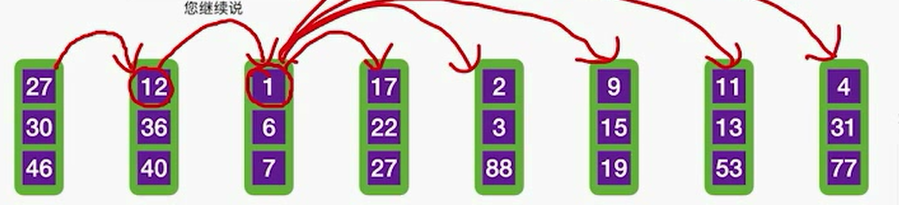

作用：在外部排序方法中，为了减少I/O次数，而需要将二路平衡归并改为多路平衡归并，但是按照原有的归并算法，将二路归并改为多路归并将增加其内部排序的时间。为了是内部排序不受到归并数目的影响，从而引入了败者树的概念。
概念：败者树是对树形选择排序的一种变化，它是一颗完全二叉树。每个叶子节点存放各个归并段在当前位置需要参加归并的记录，其内部节点用来记录左右子数中的“失败者”，从而让胜利者继续比较，一直到跟节点。根据需求可以将左右子树中大的（小的）定义为失败者，小的（大的）为胜利者，则根节点指向的数为最小数（最大数）。

下面以大的为失败者，小的为胜利者解释。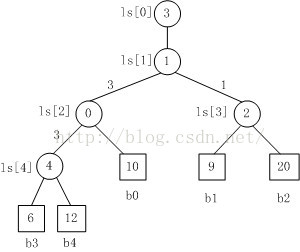

如上图所示：有b0、b1、b2、b3、b4五个归并路数，它们的值分别是10、9、20、6、12.

• b3和b4比较，b3为胜利者，于是将失败者b4的路号4存入b3、b4的父节点中；
• 将胜利者b3继续与b0相比，b3对应的是6，b4对应的是10，于是b3为胜利者，b0为失败者，将失败者b0的路号0存入到上一层父节点中；
• 再看右边b1和b2的比较，b1对应的是9，b2对应的是20，于是b1为胜利者，b2为失败者，将失败者b2的路号2存入到b1、b2的父节点中；
• 然后将左边的胜者b3与右边的胜者b1比较，b3对应的是6，b1对应的是9，则b3为胜者，b1为败者，将失败者b1的路号1存入到上一层父节点中；
• 最后在将胜利者的路号写入ls[0]中

python 源码：

#!/usr/bin/env python
# -*- coding: utf-8 -*-
"""
参考资料：
http://sshpark.com.cn/2018/11/22/%E6%95%B0%E6%8D%AE%E7%BB%93%E6%9E%84%EF%BC%9A%E8%B4%A5%E8%80%85%E6%A0%91/
https://www.it610.com/article/1305779568971386880.htm
"""
K = 4  # 4路归并
buf = []  # 存放多路归并的头元素，多出来的一位放最小值
ls = []  # ls[0]保存的是胜者的下标，其余保存败者下标号
def adjust(index):
    """定义调整函数 s是buf数组的下标"""
    f_index = (index + K) // 2  # 取s位的父节点
    # 如果当前节点不是根节点则进入下次循环，否则跳出
    while f_index > 0:
        # 比较当前节点值与父节点对应的值，如果父节点胜出则记录失败者并将当前节点换成胜利者(当前规则：大者为败，小者为胜)
        if buf[index] > buf[ls[f_index]]:
            l = ls[f_index]
            ls[f_index] = index
            index = l
        f_index = f_index // 2
    # 记录最终胜利者到ls[0]
    ls[0] = index
def build():
    """定义败者树构建函数"""
    # 添加最小值-1到buf尾部
    buf.append(-1)
    # 将败者树中间节点全部初始化为最小值所在位置即len(buf)-1
    for i in range(len(buf)):
        ls.append(len(buf) - 1)
    # 依次调整buf列表中所有位置
    for i in range(K):
        adjust(i)
def get_min():
    return buf[ls[0]]
if __name__ == '__main__':
    buf = [12, 7, 6, 8]
    build()
    print(get_min())
    buf[2] = 11
    adjust(2)
    print(get_min())
    pass

参考资料：

• 败者树
• csdn-败者树