Day 27 | 39.组合总和、40.组合总和 II、131.分割回文串 - 《代码随想录算法训练营》

Leetcode 39.组合总和
Leetcode 40.组合总和 II
Leetcode 131.分割回文串

Leetcode 39.组合总和

题目：39.组合总和

初始思路

和77.组合的区别在于，这里的元素可以重复使用，所以递归退出的条件就不能是个数。只能通过sum和target的关系判断。

代码

var combinationSum = function (candidates, target) {
    let res = []
    let path = []
    // 从小到大排序
    candidates.sort((a, b) => a - b)
    const backtracking = (startIndex, sum) => {
        if (sum === target) {
            res.push([...path])
            return
        }
        for (let i = startIndex; i < candidates.length; i++){
            const n = candidates[i]
            // 如果和大于target就终止遍历
            if (n + sum > target) break
            path.push(n)
            sum += n
            backtracking(i, sum)
            // 回溯
            path.pop()
            sum -= n
        }
    }
    backtracking(0, 0)
    return res
};

感想

图示
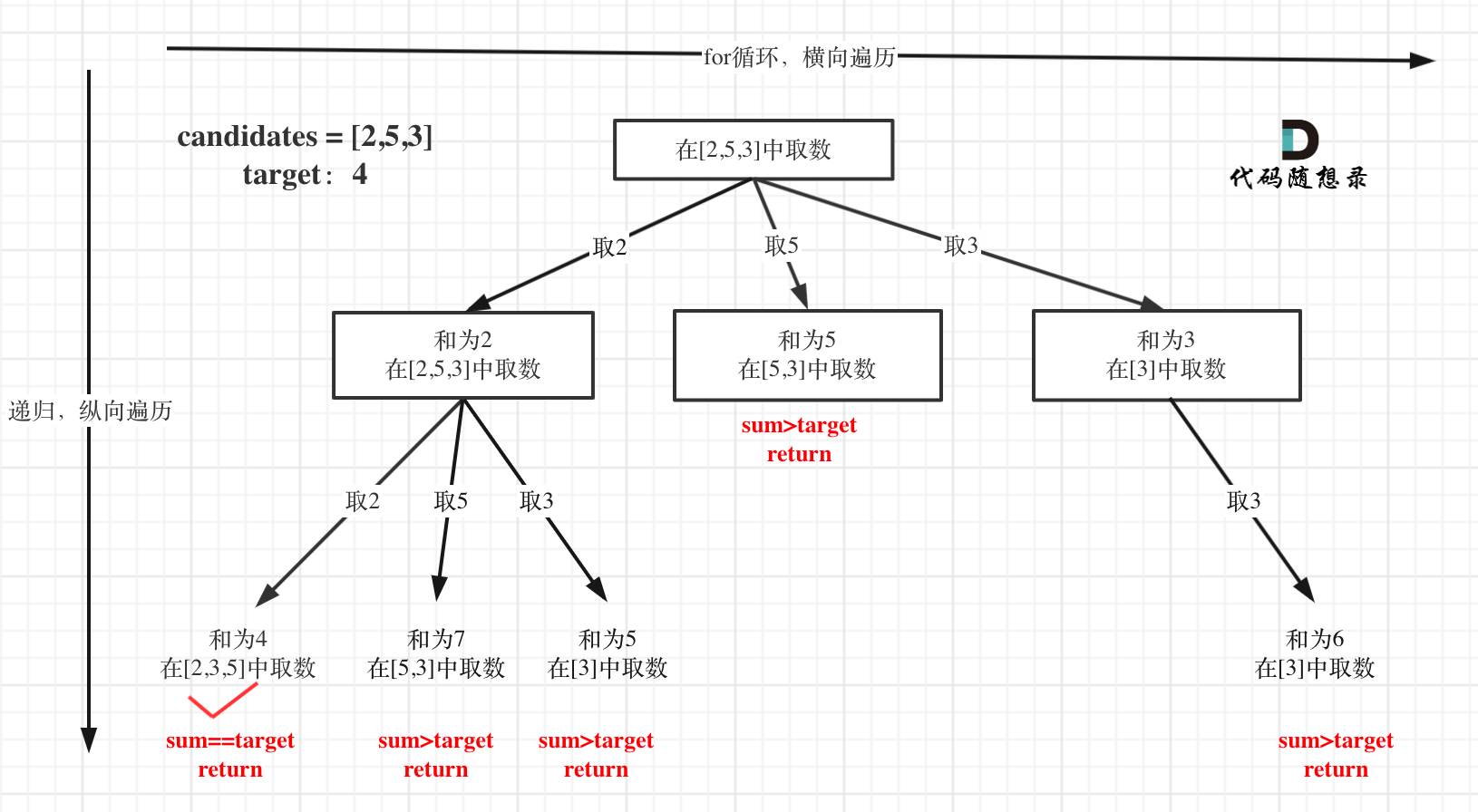
主要要看懂回溯操作，相比较77更改了一些条件。有startIndex就会排除已经选取过的元素。

Leetcode 40.组合总和 II

题目：40.组合总和 II

初始思路

跟上一题比较，这题每个数字只能重复一次，但是给的数组里面元素是有重复的。也就是说每个解的内部是可以由重复元素的（次数最多和原数组一样）

代码

var combinationSum2 = function (candidates, target) {
    let res = []
    let path = []
    let sum = 0
    const len = candidates.length
    // 从小到大排序
    candidates.sort((a, b) => a - b)
    // 标记数组
    let used = new Array(len).fill(false)
    const backtracking = (startIndex) => {
        if (sum === target) {
            res.push([...path])
            return
        }
        for (let i = startIndex; i < len && sum < target; i++){
            const n = candidates[i]
            // 如果n === candidates[i - 1]说明和前一个元素重复了，检查一下used数组，如果是false说明同一层candidates[i-1]使用过
            if (n + sum > target || (i > 0 && n === candidates[i - 1] && !used[i - 1])) continue
            path.push(n)
            sum += n
            used[i] = true
            backtracking(i + 1)
            // 回溯
            path.pop()
            sum -= n
            used[i] = false
        }
    }
    backtracking(0)
    return res
};

var combinationSum2 = function (candidates, target) {
    let res = []
    let path = []
    let sum = 0
    const len = candidates.length
    // 从小到大排序
    candidates.sort((a, b) => a - b)
    // 标记数组
    const backtracking = (startIndex) => {
        if (sum === target) {
            res.push([...path])
            return
        }
        for (let i = startIndex; i < len; i++) {
            const n = candidates[i]
            if (i > startIndex && candidates[i] === candidates[i - 1]) {
                //若当前元素和前一个元素相等
                //则本次循环结束，防止出现重复组合
                continue
            }
            //如果当前元素值大于目标值-总和的值
            //由于数组已排序，那么该元素之后的元素必定不满足条件
            //直接终止当前层的递归
            if (n + sum > target) break
            path.push(n)
            sum += n
            backtracking(i + 1)
            // 回溯
            path.pop()
            sum -= n
        }
    }
    backtracking(0)
    return res
};

感想

回看一下题目，元素在同一个组合内是可以重复的，怎么重复都没事，但两个组合不能相同。
所以我们要去重的是同一树层上的“使用过”，同一树枝上的都是一个组合里的元素，不用去重。
图示

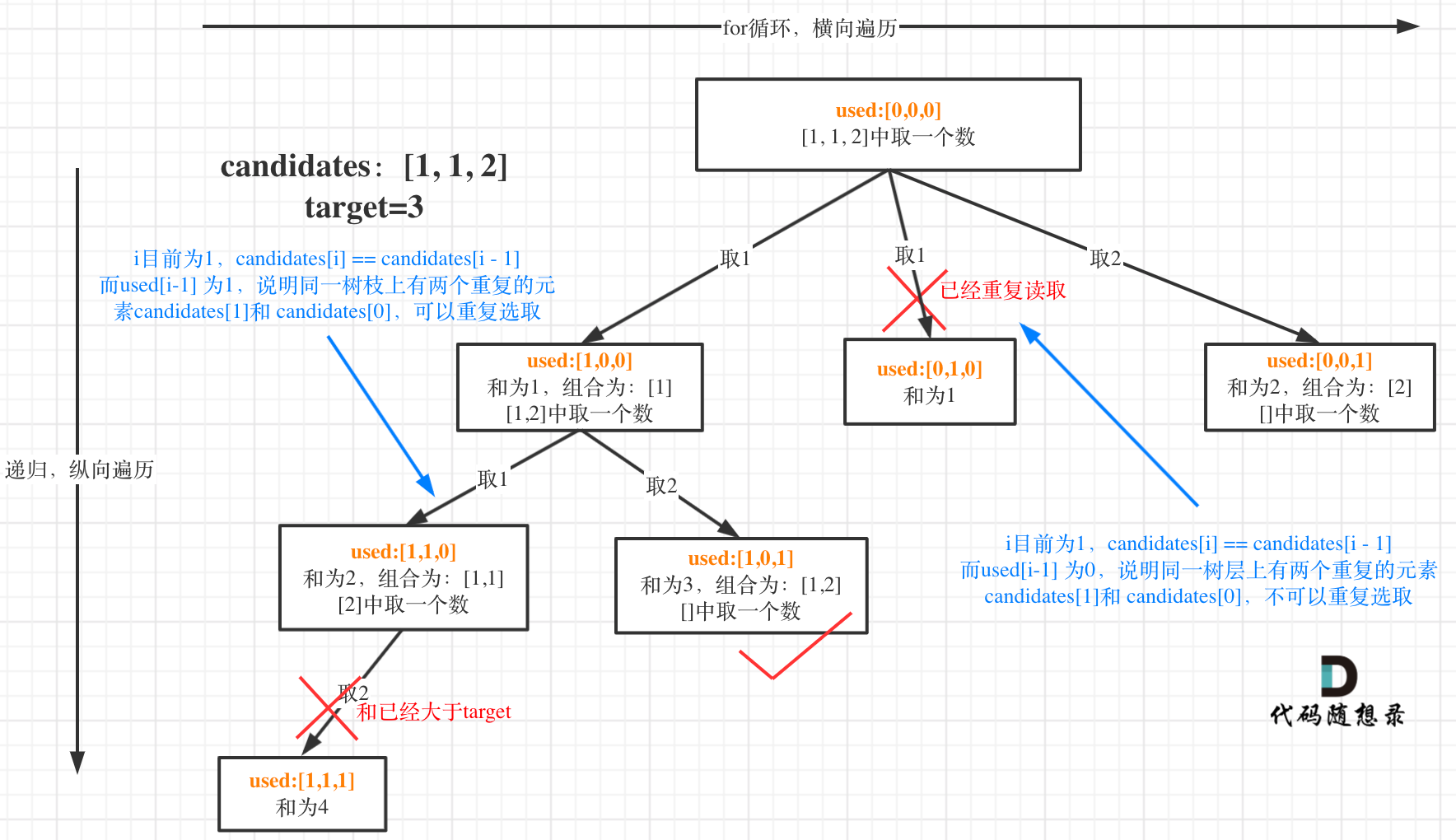
Leetcode 131.分割回文串

题目：131.分割回文串

初始思路

回文字符串用双指针判断，一前一后往中间夹。

代码

const isPalindrome = (str, left, right) => {
    for (let i = left, j = right; i < j; i++, j--) {
        if (str[i] !== str[j]) return false
    }
    return true
}
var partition = function (s) {
    let res = []
    let path = []
    const len = s.length
    const backtracking = (startIndex) => {
        if (startIndex >= len) {
            res.push([...path])
            return
        }
        for (let i = startIndex; i < len; i++) {
            if (!isPalindrome(s, startIndex, i)) continue
            // 截取这段字符串，注意左闭右开
            path.push(s.slice(startIndex, i + 1))
            // 因为不能重复，所以+1
            backtracking(i + 1)
            // 回溯
            path.pop()
        }
    }
    backtracking(0)
    return res
};

感想

具体来说, 给定一个字符串s, 长度为n, 它成为回文字串的充分必要条件是s[0] == s[n-1]且s[1:n-1]是回文字串。
好难！