Day 29 | 491.递增子序列、46.全排列、47.全排列 II

Leetcode 491.递增子序列

题目：491.递增子序列

初始思路

求自增子序列，不能对原序列进行排序。

代码

var findSubsequences = function (nums) {
    let res = []
    let path = []
    const backtracking = (startIndex) => {
        if (path.length > 1) {
            res.push([...path])
            // 注意这里不要return，要取树上的节点
        }
        let uesd = []
        for (let i = startIndex; i < nums.length; i++){
            if ((path.length > 0 && nums[i] < path[path.length - 1]) || uesd[nums[i] + 100]) {
                continue
            }
            // 因为题目给的数字范围是 -100 ~ 100
            // 标记为使用过了
            uesd[nums[i] + 100] = true
            path.push(nums[i])
            backtracking(i + 1)
            // 回溯
            path.pop()
        }
    }
    backtracking(0)
    return res
};

感想

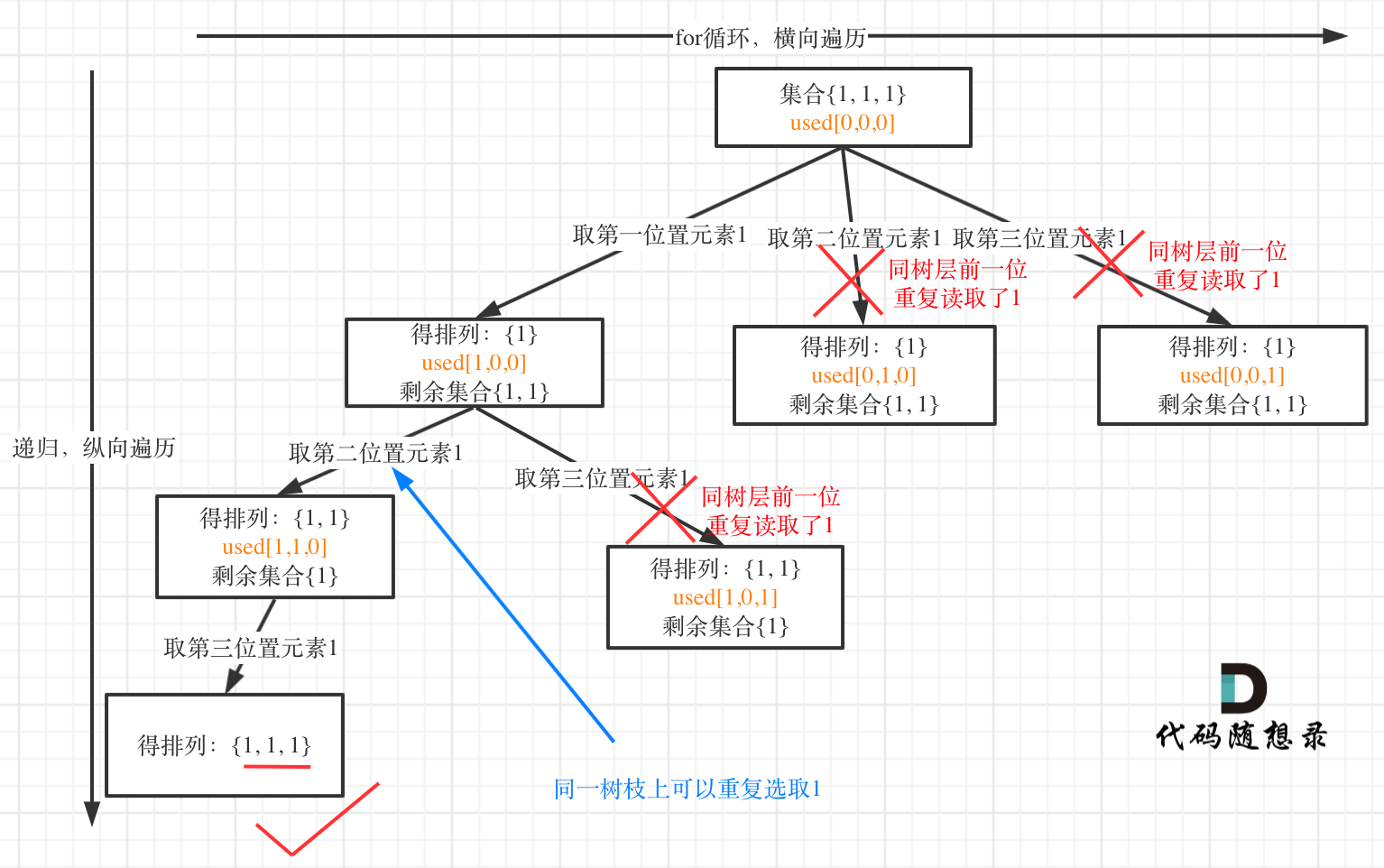
1. 一个元素不能重复使用，所以需要startIndex，调整下一层递归的起始位置。
2. 图示
   

Leetcode 46.全排列

题目：46.全排列

初始思路

这题就是排列了，不是组合，不同的顺序代表不同的排列。

代码

var permute = function (nums) {
    let res = []
    let path = []
    const backtracking = (uesd) => {
        // 如果路径的长度达到了nums的长度，说明找到了一种排列
        if (path.length === nums.length) {
            res.push([...path])
            return
        }
        // 因为是排列不是组合,所以是从0开始
        for (let i = 0; i < nums.length; i++) {
            // path里已经收录的元素，直接跳过
            if (uesd[i]) continue
            path.push(nums[i])
            // 标记为使用过 一个排列里一个元素只能使用一次
            uesd[i] = true
            backtracking(uesd)
            // 回溯
            path.pop()
            uesd[i] = false
        }
    }
    backtracking([])
    return res
};

感想

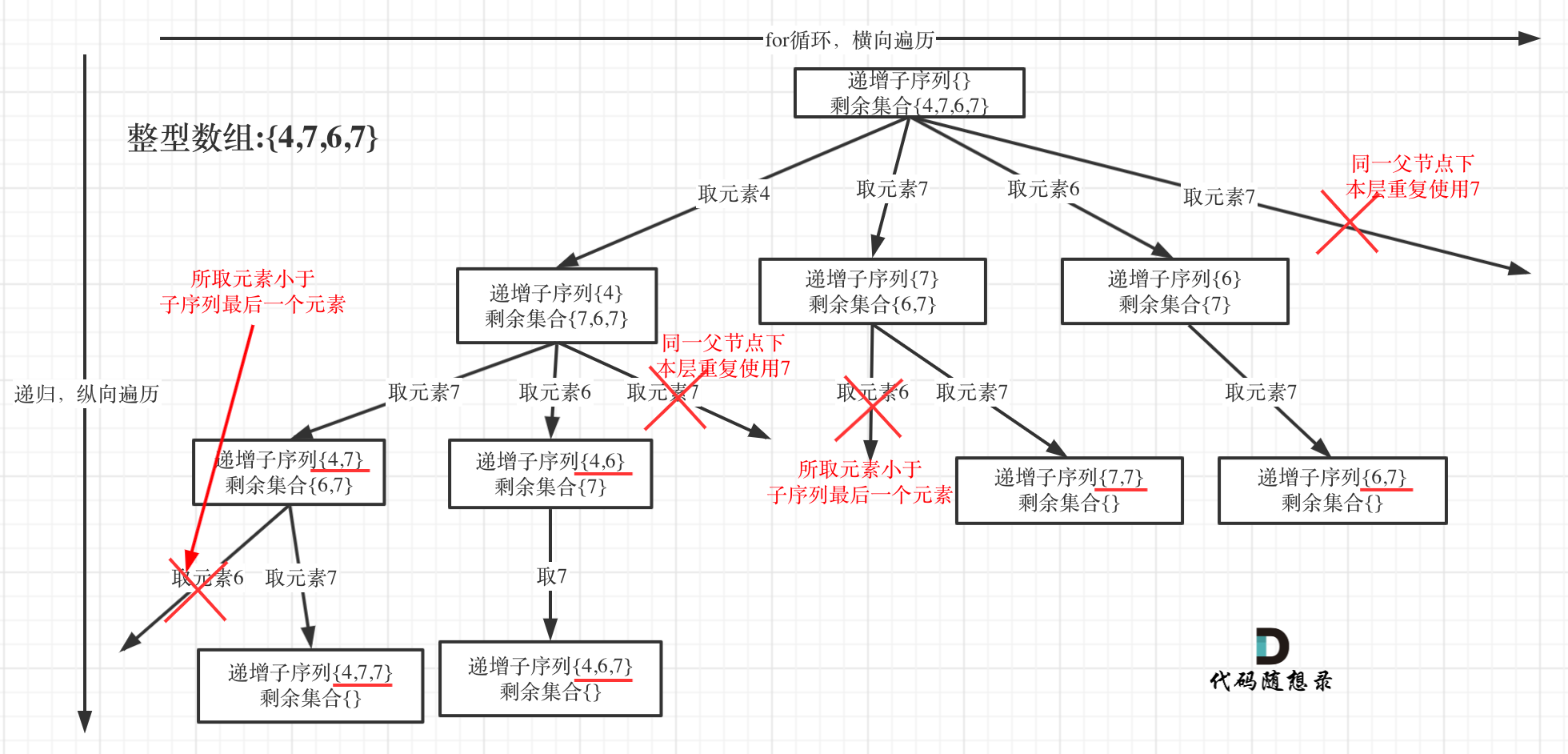
1. 首先排列是有序的，也就是说 [1,2] 和 [2,1] 是两个集合，这和之前分析的子集以及组合所不同的地方。
2. 可以看出元素1在[1,2]中已经使用过了，但是在[2,1]中还要在使用一次1，所以处理排列问题就不用使用startIndex了。
3. 

Leetcode 47.全排列 II

题目：47.全排列 II

初始思路

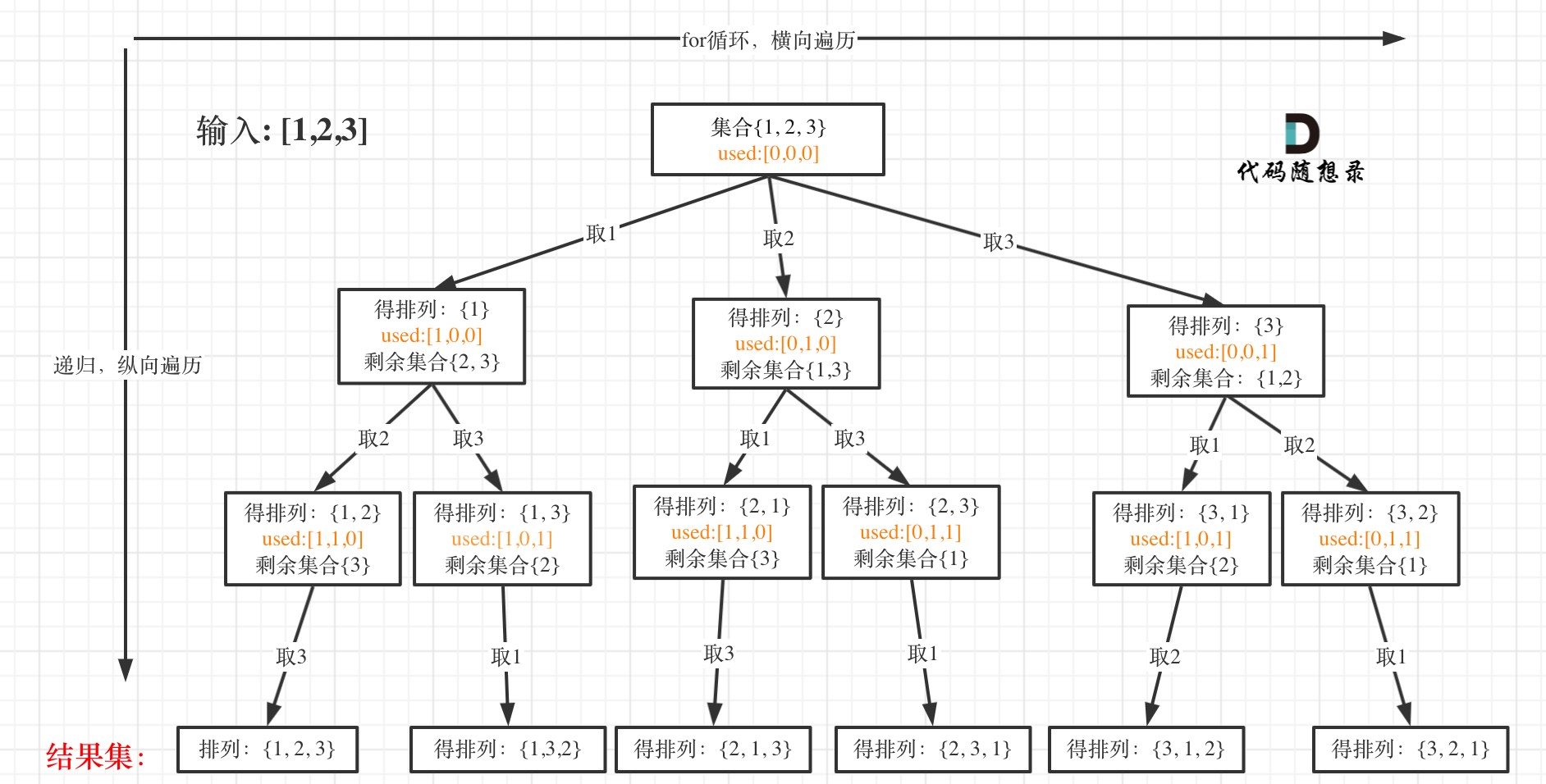
相比上题给的nums里面多了重复的数字，要返回所有不重复的全排列。

代码

var permuteUnique = function (nums) {
    let res = []
    let path = []
    nums.sort((a, b) => a - b)
    const backtracking = (used) => {
        // 如果路径的长度达到了nums的长度，说明找到了一种排列
        if (path.length === nums.length) {
            res.push([...path])
            return
        }
        // 因为是排列，所以从0开始
        for (let i = 0; i < nums.length; i++){
            // used[i - 1] == true 说明同一树枝nums[i - 1]使用过
            // used[i - 1] == false 说明同一树层nums[i - 1]使用过
            // 如果遇到同一树层nums[i - 1]使用过则直接跳过
            if (i > 0 && nums[i] === nums[i - 1] && !used[i - 1]) {
                continue
            }
            // 如果同一树枝nums[i]没使用过开始处理
            if (!used[i]) {
                used[i] = true
                path.push(nums[i])
                backtracking(used)
                // 回溯
                path.pop()
                used[i] = false
            }
        }
    }
    backtracking([])
    return res
};

感想

1. 在40.组合总和II、90.子集II分别详细讲解了组合问题和子集问题如何去重。
2.