Day 41 | 343.整数拆分、96.不同的二叉搜索树

Leetcode 343.整数拆分

题目：343.整数拆分 讲解：代码随想录

初始思路

和相同的话，拆成的数字越靠近的话积越大，但是拆成几个数字呢。

代码

var integerBreak = function (n) {
    let dp = new Array(n + 1).fill(0)
    // 初始化 题目给的n范围就是 2 <= n <= 58
    dp[2] = 1
    for (let i = 3; i <= n; i++){
        for (let j = 1; j < i; j++){
            dp[i] = Math.max(dp[i], dp[i - j] * j, (i - j) * j)
        }
    }
    return dp[n]
};

感想

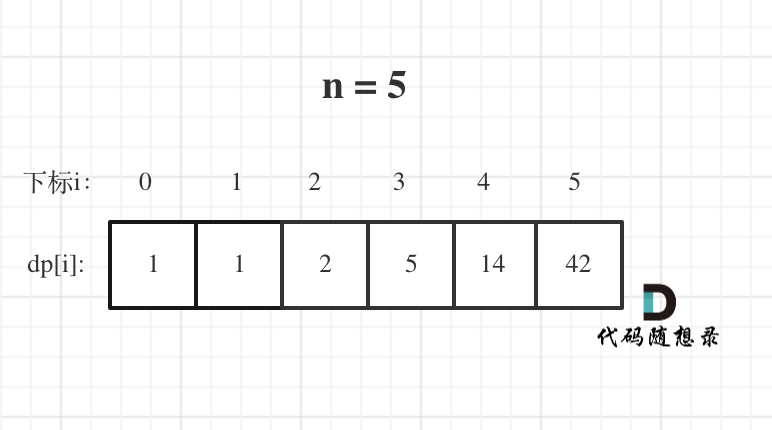
1. 确定dp数组以及下标含义：dp[i]：分拆数字i，可以得到的最大乘积为dp[i]。
2. 确定递推公式：
   
3. dp数组的初始化：只初始化dp[2] = 1，从dp[i]的定义来说，拆分数字2，得到的最大乘积是1，这个没有任何异议！
4. 确定遍历顺序：
   
5. 举例推导dp数组：
   

Leetcode 96.不同的二叉搜索树

题目：96.不同的二叉搜索树 讲解：代码随想录

初始思路

代码随想录讲解的很详细

代码

var numTrees = function (n) {
    //初始化 dp 数组
    let dp = new Array(n + 1).fill(0)
    //初始化0个节点和1个节点的情况
    dp[0] = 1
    dp[1] = 1
    for (let i = 2; i <= n; i++) {
        for (let j = 1; j <= i; j++) {
            //对于第i个节点，需要考虑1作为根节点直到i作为根节点的情况，所以需要累加
            //一共i个节点，对于根节点j时,左子树的节点个数为j-1，右子树的节点个数为i-j
            dp[i] += dp[i - j] * dp[j - 1]
        }
    }
    return dp[n]
};

感想

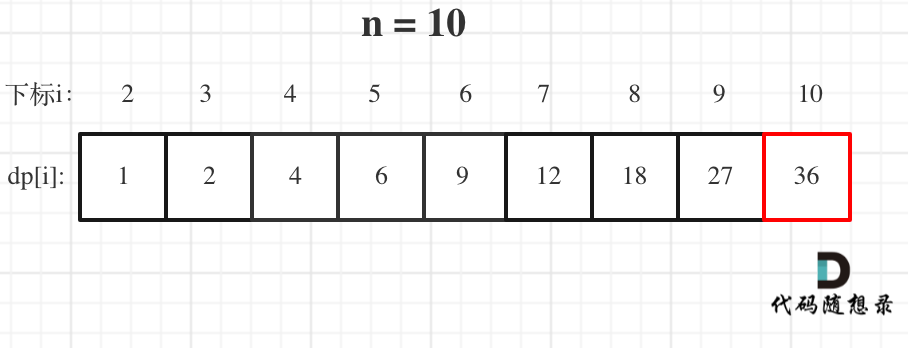
1. 确定dp数组以及下标的含义：dp[i] ： 1到i为节点组成的二叉搜索树的个数为dp[i]。
2. 确定递推公式：所以递推公式：dp[i] += dp[j - 1] * dp[i - j]; ，j-1 为j为头结点左子树节点数量，i-j 为以j为头结点右子树节点数量
3. dp数组初始化：从递归公式上来讲，dp[以j为头结点左子树节点数量] * dp[以j为头结点右子树节点数量] 中以j为头结点左子树节点数量为0，也需要dp[以j为头结点左子树节点数量] = 1， 否则乘法的结果就都变成0了。所以初始化dp[0] = 1
4. 确定遍历顺序：首先一定是遍历节点数，从递归公式：dp[i] += dp[j - 1] * dp[i - j]可以看出，节点数为i的状态是依靠 i之前节点数的状态。那么遍历i里面每一个数作为头结点的状态，用j来遍历。
5. 举例推导dp数组：