Day 18 | 513.找树左下角的值、112.路径总和、113.路径总和 II、106.从中序与后序遍历序列构造二叉树、105.从前序与中序遍历序列构造二叉树

Leetcode 513.找树左下角的值

题目：513.找树左下角的值

初始思路

利用层序遍历模板可以套出来

代码

var findBottomLeftValue = function (root) {
    if (!root) return null
    let queue = []
    queue.push(root)
    let res
    while (queue.length) {
        let length = queue.length
        for (let i = 0; i < length; i++){
            let node = queue.shift()
            if (i === 0) {
                res = node.val
            }
            if (node.left) {
                queue.push(node.left)
            }
            if (node.right) {
                queue.push(node.right)
            }
        }
    }
    return res
};

var findBottomLeftValue = function (root) {
    let maxPath = 0, resNode = null
    const dfsTree = function (node, curPath) {
        if (node.left == null && node.right == null) {
            if (curPath > maxPath) {
                // 更新最大深度
                maxPath = curPath
                // 最大深度最左边的数值
                resNode = node.val
            }
        }
        // 单层递归逻辑
        if (node.left) {
            dfsTree(node.left, curPath + 1)
        }
        if (node.right) {
            dfsTree(node.right, curPath + 1)
        }
    }
    dfsTree(root, 1)
    return resNode
}

感想

1. 这题层序遍历模板比递归简单。递归需要考虑如何找到最下面一层。然后再找到最左边的节点。

Leetcode 112.路径总和

题目：112.路径总和 讲解：https://www.bilibili.com/video/BV19t4y1L7CR

初始思路

之前有道题是求所有路径，对所有路径再求和的话也可以写出来，但是可能会多遍历一些不必要的路径。

代码

var hasPathSum = function (root, targetSum) {
    const traversal = function (node, cnt) {
        // 结束条件
        if (cnt === 0 && node.left == null && node.right== null) {
            // 如果遇到叶子节点的时候并且计数为0，说明正好是我们需要的路径
            return true
        }
        if (cnt !== 0 && node.left == null && node.right == null) {
            // 遇到了叶子节点，但是计数不为0，直接返回
            return false
        }
        //  左（空节点不遍历）.遇到叶子节点返回true，则直接返回true
        if (node.left != null && traversal(node.left, cnt - node.left.val)) {
            return true
        }
        //  右（空节点不遍历）
        if (node.right != null && traversal(node.right, cnt - node.right.val)) {
            return true
        }
        return false
    }
    if (!root) return false
    // 把目标值传进去，每经过一个节点就减去这个节点的值，如果最后是0的话说明是我们要的路径。不采用累加的做法
    return traversal(root, targetSum - root.val)
};

// 迭代
var hasPathSum = function (root, targetSum) {
    if (!root) return false
    let nodeArr = [root]
    let valArr = [0]
    while (nodeArr.length) {
        let curNode = nodeArr.shift()
        let curVal = valArr.shift()
        curVal += curNode.val
        // 为叶子结点，且和等于目标数，返回true
        if (curVal === targetSum && curNode.left == null && curNode.right == null) {
            return true
        }
        // 左
        if (curNode.left) {
            // 放入下一个左节点
            nodeArr.push(curNode.left)
            // 放入当前路径的和
            valArr.push(curVal)
        }
        // 右
        if (curNode.right) {
            // 放入下一个左节点
            nodeArr.push(curNode.right)
            // 放入当前路径的和
            valArr.push(curVal)
        }
    }
    return false
}

感想

1. 递归的做法更容易理解。采用传入目标值，然后经过路径的时候相减。最后等于0的时候说明是要找的路径
2. 迭代法利用的是求和累加，每路过一个节点就加上这个节点的值。

Leetcode 113.路径总和 II

题目：113.路径总和 II

初始思路

相比上一题直接返回布尔值，这题需要返回满足条件的路径。需要同时记录下路径。

代码

var pathSum = function (root, targetSum) {
    const res = []
    const traversal = function (node, cnt, path) {
        // 判断路径
        if (cnt === 0 && node.left == null && node.right == null) {
            // 因为path是一个数组，所以需要解构赋值之后把值放进去
            res.push([...path])
            return
        }
        if (cnt !== 0 && node.left == null && node.right == null) {
            // 遇到了叶子节点，但是计数不为0
            return
        }
        // 左 （空节点不遍历）
        if (node.left) {
            path.push(node.left.val)
            // 递归
            traversal(node.left, cnt - node.left.val, path)
            // 回溯
            path.pop()
        }
        // 右 （空节点不遍历）
        if (node.right) {
            path.push(node.right.val)
            // 递归
            traversal(node.right, cnt - node.right.val, path)
            // 回溯
            path.pop()
        }
        return
    }
    if (!root) return res
    // 把根节点的值减掉当做初始值。把根节点放入路径中
    traversal(root, targetSum - root.val, [root.val])
    return res
};

// 迭代
var pathSum = function (root, targetSum) {
    if (!root) return []
    let nodeArr = [root]
    let resArr = [] // 记录符合目标和的返回路径
    let tempArr = [[]] // 对应路径
    let countArr = [0] //对应和
    while (nodeArr.length) {
        let curNode = nodeArr.shift()
        let curVal = countArr.shift()
        let path = tempArr.shift()
        curVal += curNode.val
        path.push(curNode.val)
        // 为叶子结点，且和等于目标数，将此次结果数组push进返回数组中
        if (curVal === targetSum && curNode.left == null && node.right == null) {
            resArr.push(path)
        }
        // 左，将当前的和及对应路径也对应记录下来
        if (curNode.left) {
            nodeArr.push(curNode.left)
            countArr.push(curVal)
            tempArr.push([...path])
        }
        // 右，将当前的和及对应路径也对应记录下来
        if (curNode.right) {
            nodeArr.push(curNode.right)
            countArr.push(curVal)
            tempArr.push([...path])
        }
    }
    return resArr
}

感想

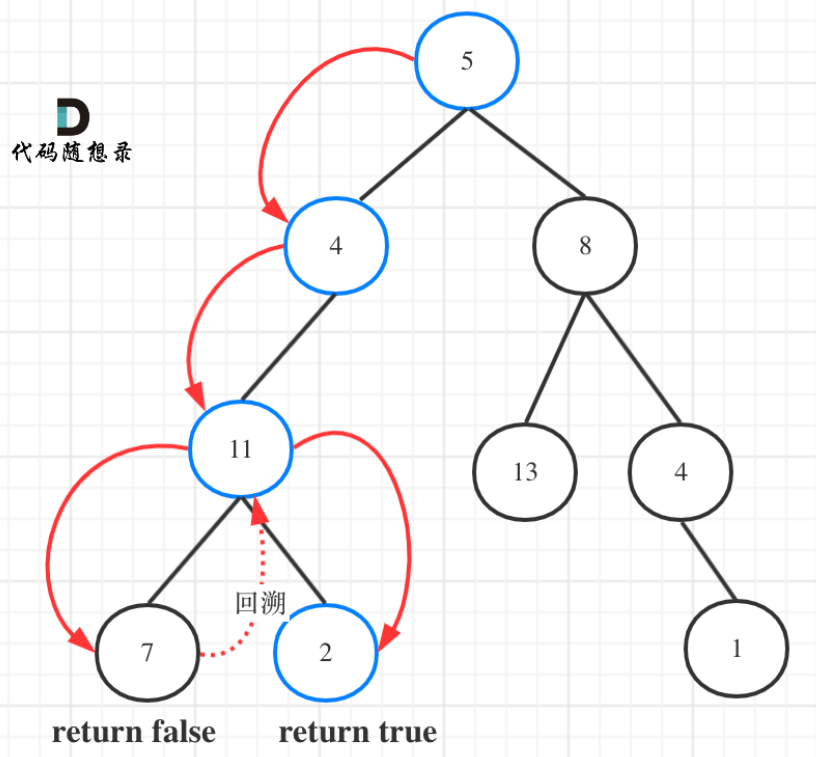
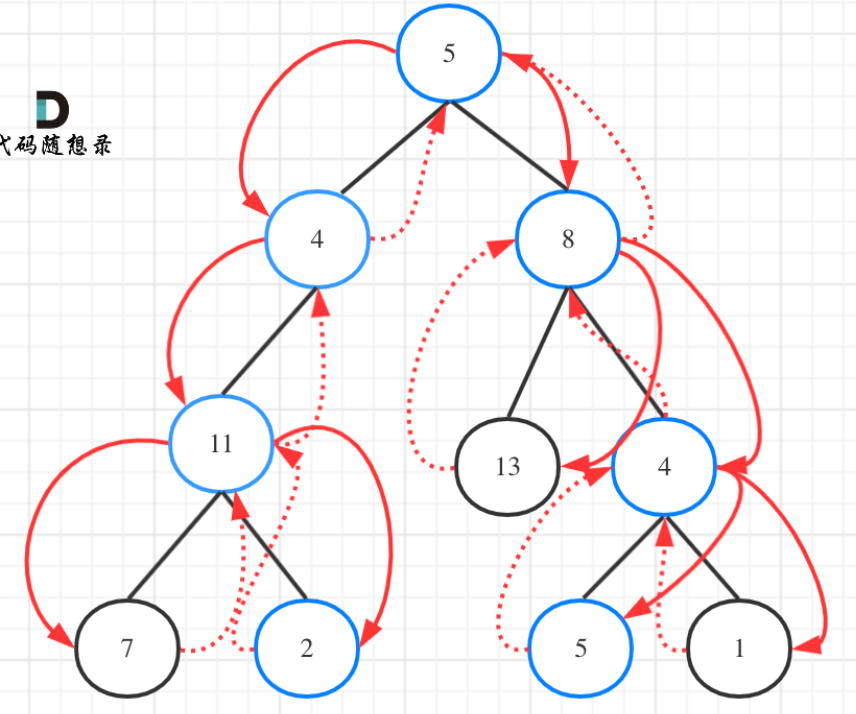
1. 当在遍历的时候走到叶子节点的时候需要回溯，回到父节点。回溯有些没理解。
2. 图示：
   
   

Leetcode 106.从中序与后序遍历序列构造二叉树

题目：106.从中序与后序遍历序列构造二叉树 讲解：https://www.bilibili.com/video/BV1vW4y1i7dn

初始思路

数据结构经典问题，根据中序和后序构造二叉树。
因为后序是左右中，所以可以从最后一个节点获得根节点，然后再中序中找到这个根节点，确定左右节点分别是哪些。

代码

var buildTree = function (inorder, postorder) {
    if (!inorder.length) return null
    // 从后序遍历的数组中获取中间节点的值， 即数组最后一个值
    const rootVal = postorder.pop()
    // 获取中间节点在中序中的下标
    let rootIndex = inorder.indexOf(rootVal)
    // 创建中间节点
    const root = new TreeNode(rootVal)
    // 构造左子树
    root.left = buildTree(inorder.slice(0, rootIndex), postorder.slice(0, rootIndex))
    // 构造右子树
    // 注意在前序数组切割中避开中间的元素
    root.right = buildTree(inorder.slice(rootIndex + 1), postorder.slice(rootIndex))
    return root
};

感想

1. 思路简单但是代码不好写。
2. 学会切割！

Leetcode 105.从前序与中序遍历序列构造二叉树

题目：105.从前序与中序遍历序列构造二叉树

初始思路

和上一题一样的思路，只不过前序的顺序是中左右，所以中节点出现在第一个元素，而后序遍历的中节点出现在最后一个元素。

代码

var buildTree = function (preorder, inorder) {
    if (!preorder.length) return null
    // 从后序遍历的数组中获取中间节点的值， 即数组第一个值。
    const rootVal = preorder.shift()
    // 获取中间节点在中序中的下标
    let rootIndex = inorder.indexOf(rootVal)
    // 创建中间节点
    const root = new TreeNode(rootVal)
    // 构造左子树
    root.left = buildTree(preorder.slice(0, rootIndex), inorder.slice(0, rootIndex))
    // 构造右子树
    // 注意在中序数组切割中避开中间的元素
    root.right = buildTree(preorder.slice(rootIndex), inorder.slice(rootIndex + 1))
    return root
};

感想

1. pop和shift方法都会操作原数组，此时数组已经改变了。
2. 注意切割的方法，slice(start,end)不包括end，所以是左闭右开。
3. 如果给前序和后序是不能构造出二叉树的，必须要有中序来确定左子树和右子树。