剑指 Offer 47. 礼物的最大价值

剑指 Offer 47. 礼物的最大价值

解题思路：动态规划

动态规划的解题步骤：

1. 状态定义
2. 确定状态转移方程与初始值
3. 递推实现

状态定义

我们定义 dp 矩阵，dp(i,j) 代表从棋盘的左上角开始到达单元格 (i,j) 时能够拿到礼物的最大累计价值。

确定状态转移方程与初始值

• i = 0 , j = 0 时，此时我们只能拿到 grid[0][0] 的礼物，所以累计价值为：dp[0][0] = grid[0][0]
• i = 0 , j ≠ 0 时，也就是对应矩阵的第一行，我们只能从左边到达
• i ≠ 0 , j = 0 时，也就是对应矩阵的第一列，我们只能从上边到达
• i ≠ 0 , j ≠ 0 时，可以从左边或上边到达

我们可以总结出状态转移方程：

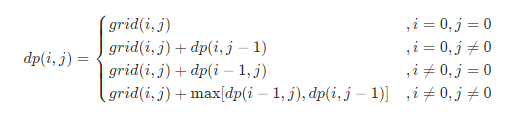
代码

class Solution {
    public int maxValue(int[][] grid) {
        int m = grid.length;
        int n = grid[0].length;
        int[][] dp = new int[m][n];
        dp[0][0] = grid[0][0];
        for(int i = 1; i < grid[0].length; i++){
            dp[0][i] = grid[0][i] + dp[0][i - 1];
        }
        for(int i = 1; i < grid.length; i++){
            dp[i][0] = grid[i][0] + dp[i - 1][0];
        }
        for(int i = 1; i < grid.length; i++){
            for(int j = 1; j < grid[0].length; j++){
                dp[i][j] = Math.max(dp[i - 1][j],dp[i][j - 1]) + grid[i][j];
            }
        }
        return dp[m - 1][n - 1];
    }
}

空间复杂度的优化：

上述代码中，我们新开辟了矩阵 dp 定义到达每个格子时礼物的累计最大值，很显然这浪费了 O(MN) 的额外空间。

我们可以做原地 dp，即：在原数组上进行修改，以达到节省空间的目的。

代码如下：

class Solution {
    public int maxValue(int[][] grid) {
        for(int i = 1; i < grid[0].length; i++){
            grid[0][i] += grid[0][i - 1];
        }
        for(int i = 1; i < grid.length; i++){
            grid[i][0] += grid[i - 1][0];
        }
        for(int i = 1; i < grid.length; i++){
            for(int j = 1; j < grid[0].length; j++){
                grid[i][j] += Math.max(grid[i - 1][j],grid[i][j - 1]);
            }
        }
        return grid[grid.length - 1][grid[0].length - 1];
    }
}

复杂度分析

• 时间复杂度：O(MN)

M，N 分别表示矩阵的行高与列宽，我们需要遍历整个矩阵，所以时间复杂度为 O(MN)

• 空间复杂度：O(1)

原地 dp 使用了常数大小的额外空间