剑指 Offer 49. 丑数

解题思路：动态规划

丑数的递推性质：

丑数只包含因子 2，3，5，因此有结论：丑数 = 某较小丑数 × 某因子

设长度为 n 的丑数序列为 ：X1,X2, … ,Xn , 求第 n + 1 个丑数 Xn + 1

根据丑数的递推性质，我们知道，丑数 Xn + 1 只可能为以下三种情况之一：

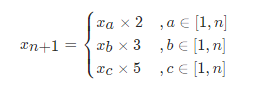
image.png

动态规划的解题步骤：

  1. 状态定义
  2. 确定状态转移方程与初始值
  3. 递推实现

状态定义

定义 dp 数组，dp[i] 表示第 i - 1 个丑数的值

确定状态转移方程与初始值

方程初始值为 dp[0] = 1

创建三个索引值，分别代表丑数 2，3，5 的索引

  1. int a = 0; // index of 2
  2. int b = 0; // index of 3
  3. int c = 0; // index of 5

状态转移方程如下：

  1. dp[i] = min(dp[a] * 2,dp[b] * 3,dp[c] * 5);

代码

  1. class Solution {
  2.     public int nthUglyNumber(int n) {
  3.         // dp[i] 表示第i - 1个丑数的值
  4.         int[] dp = new int[n];
  5.         int a = 0; // index of 2
  6.         int b = 0; // index of 3
  7.         int c = 0; // index of 5
  9.         // dp[0] 表示 第1个丑数的值
  10.         dp[0] = 1;
  12.         for(int i = 1; i < n; i++){
  13.             dp[i] = Math.min(Math.min(dp[a] * 2,dp[b] * 3),dp[c] * 5);
  14.             if(dp[i] == dp[a] * 2) a++;
  15.             if(dp[i] == dp[b] * 3) b++;
  16.             if(dp[i] == dp[c] * 5) c++;
  17.         }
  18.         return dp[n - 1];
  19.     }
  20. }

复杂度分析

  • 时间复杂度：O(N)

动态规划需要遍历 dp 列表，所以时间复杂度为 O(N)

  • 空间复杂度：O(N)

我们需要额外创建 dp 数组，使用了 O(N) 的额外空间