剑指 Offer 35. 复杂链表的复制

剑指 Offer 35. 复杂链表的复制

解题思路1：哈希表

示例：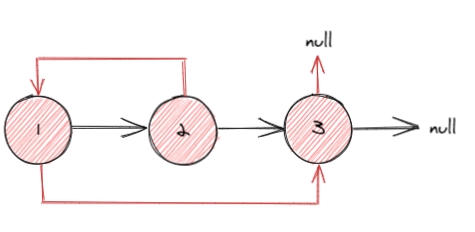

示例中，黑色的箭头表示为 next 指针，红色的箭头表示为 random 指针

我们可以使用哈希表，哈希表的键存储原链表的节点，哈希表的值存储复制后的节点。

链表中的原节点记作 node，复制后的节点记作 node’

两者之间具有如下关系：

• node'.next = map.get(node.next)
• node'.random = map.get(node.random)

代码

/*
// Definition for a Node.
class Node {
    int val;
    Node next;
    Node random;
    public Node(int val) {
        this.val = val;
        this.next = null;
        this.random = null;
    }
}
*/
class Solution {
    public Node copyRandomList(Node head) {
        Map<Node,Node> map = new HashMap<>();
        Node cur = head;
        while(cur != null){
            map.put(cur,new Node(cur.val));
            cur = cur.next;
        }
        cur = head;
        while(cur != null){
            map.get(cur).next = map.get(cur.next);
            map.get(cur).random = map.get(cur.random);
            cur = cur.next;
        }
        return map.get(head);
    }
}

复杂度分析

• 时间复杂度：O(N)

使用哈希表，我们需要两轮遍历链表，所以时间复杂度为： O(N)

• 空间复杂度：O(N)

我们使用哈希表存储链表的节点，占用了 O(N) 的额外空间

解题思路2：拼接与拆分

第二种思路为拼接与拆分链表，可以分为三个步骤：

1. 拼接链表，将复制后的节点放到原节点之后，使用 next 指针相关联
2. 构建复制节点的 random 指针
3. 将复制后的链表从原链表中拆分出去

拼接链表

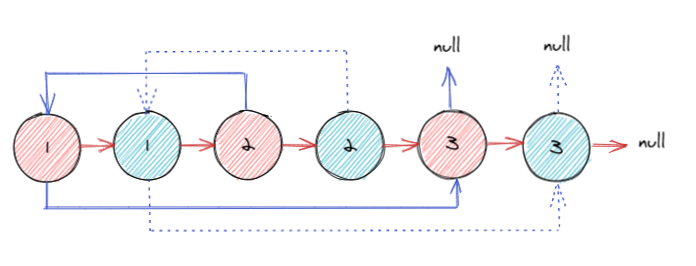
我们首先不考虑 random 指针，将链表拼接至下图所示：

蓝色的节点为复制后的节点，我们将每一个复制后的节点都放在原节点之后，使用 next 指针相连接

构建 random 指针

然后，我们构建复制后节点之间 random 指针的关联

原节点记作 node，复制后的节点记作 node’，二者之间满足：

• node.next = node'
• node'.random = node.random.next

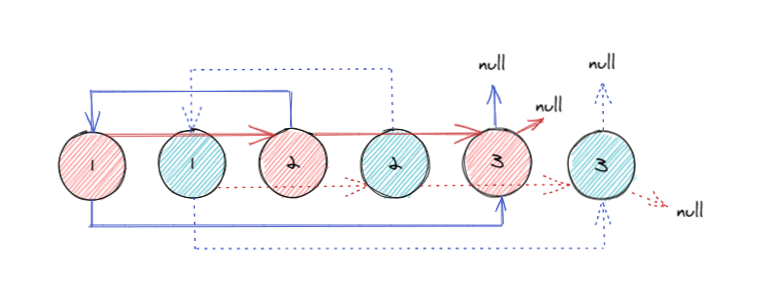
构建好 random 指针的关联后的链表如下图所示：

拆分链表

第三步，我们需要将复制后的链表从原链表中拆分出去

只需要将复制后的节点的 next 指针指向复制后的节点即可。同时我们为了不破坏原链表，还需要将原链表的节点的 next 指针指向原链表的节点。

代码

/*
// Definition for a Node.
class Node {
    int val;
    Node next;
    Node random;
    public Node(int val) {
        this.val = val;
        this.next = null;
        this.random = null;
    }
}
*/
class Solution {
    public Node copyRandomList(Node head) {
        if(head == null){
            return null;
        }
        Node cur = head;
        while(cur != null){
            Node node = new Node(cur.val);
            node.next = cur.next;
            cur.next = node;
            cur = node.next;
        } 
        cur = head;
        while(cur != null){
            cur.next.random = cur.random == null ? null :cur.random.next;
            cur = cur.next.next;
        }
        cur = head;
        Node res = head.next;
        Node cur2 = head.next;
        while(cur2.next != null){
            cur.next = cur.next.next;
            cur2.next = cur2.next.next;
            cur = cur.next;
            cur2 = cur2.next;
        }
        // 不要忘记处理原链表的尾节点
        cur.next = null;
        return res;
    }
}

复杂度分析

• 时间复杂度： O(N)

我们总共三轮遍历链表，使用 O(N) 的时间

• 空间复杂度： O(1)

我们仅使用了有限几个变量，使用了常数大小的额外空间，所以空间复杂度为 O(1)