题目链接：剑指 Offer 07. 重建二叉树

解题思路：递归

对于一棵二叉树：

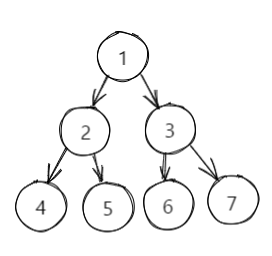
image.png
其前序遍历的结果为：

  1. 1 2 4 5 3 6 7

中序遍历的结果为：

  1. 4 2 5 1 6 3 7

我们可以发现如下规律：

  • 前序遍历的第一个节点为根节点
  • 在中序遍历的结果中，头节点左边的所有节点均在左子树，头节点右边的所有节点均在右子树

这样我们就想到了使用递归的方式去构建一棵二叉树

递归算法解析：

  • 递推参数：
    • preorder 数组
    • 前序遍历的左边界 preStart，前序遍历的右边界 preEnd
    • inorder 数组
    • 中序遍历的左边界 inStart，中序遍历的有边界 inEnd
  • 递归中止条件：

当 preStart > preEnd 或 inStart > inEnd 时，返回 null

  • 递推算法：
    • 构建二叉树的根节点 head，节点值为 preorder[preStart]
    • 遍历 inorder 数组，当 inorder[i] == preorder[preStart] 时，即找到左右子树的分界
    • 划分左右子树，并开启左右子树的递归 | | preorder 左边界 | preorder 右边界 | inorder 左边界 | inorder 右边界 | | —- | —- | —- | —- | —- | | 左子树 | preStart + 1 | preStart + i - inStart | inStart | i - 1 | | 右子树 | preStart + i - inStart + 1 | preEnd | i + 1 | inEnd |

代码

Java
_

  1. /**
  2.  * Definition for a binary tree node.
  3.  * public class TreeNode {
  4.  *     int val;
  5.  *     TreeNode left;
  6.  *     TreeNode right;
  7.  *     TreeNode(int x) { val = x; }
  8.  * }
  9.  */
  10. class Solution {
  11.     public TreeNode buildTree(int[] preorder, int[] inorder) {
  12.         return buildTree(preorder,0,preorder.length - 1,inorder,0,inorder.length - 1);
  13.     }
  15.     private TreeNode buildTree(int[] preorder,int preStart,int preEnd,int[] inorder,int inStart,int inEnd){
  16.         if(preStart > preEnd || inStart > inEnd){
  17.             return null;
  18.         }
  19.         TreeNode head = new TreeNode(preorder[preStart]);
  20.         for(int i = inStart; i <= inEnd; i++){
  21.             if(inorder[i] == preorder[preStart]){
  22.                 head.left = buildTree(preorder,preStart + 1,preStart + i - inStart,inorder,inStart,i - 1);
  23.                 head.right = buildTree(preorder,preStart + i - inStart + 1,preEnd,inorder,i + 1,inEnd);
  24.             }
  25.         }
  26.         return head;
  27.     }
  28. }

复杂度分析

  • 时间复杂度：O(N logN)

对于一个递归过程，我们可以使用 Master 主公式来计算其算法的时间复杂度。

  1. master公式：T(N) = a*T(N/b) + O(N^d)
  2. 1) log(b,a) > d -> 复杂度为O(N^log(b,a))
  3. 2) log(b,a) = d -> 复杂度为O(N^d * logN)
  4. 3) log(b,a) < d -> 复杂度为O(N^d)

b 代表的含义是递归分解成了几个子过程，a 代表的含义是一次递归子过程执行了几次，O(N^d) 表示除去递归外，额外需要的过程的时间复杂度。
本算法中，相当于将构建二叉树的过程划分为对左子树和右子树分别构建并合并的过程， a 和 b 均为 2，d 为 1。因此该算法的时间复杂度为：O(N logN)

  • 空间复杂度：O(N)

最差情况下，树退化为链表，递归深度达到 N ，占用 O(N) 额外空间；最好情况下，树为满二叉树，递归深度为 logN ，占用 O(logN) 的额外空间。按照最差的复杂度计算，该算法的额外空间复杂度为：O(N)