剑指 Offer 32 - II. 从上到下打印二叉树 II

剑指 Offer 32 - II. 从上到下打印二叉树 II

解题思路

本题与 剑指 Offer 32 - I. 从上到下打印二叉树 不同的地方在于，这道题的返回类型为 List>。也就是说，对于打印一棵二叉树，我们的每一层节点都要封装到一个 List 中，然后将每一层的 List 再次添加到整体的返回列表中。

如示例：

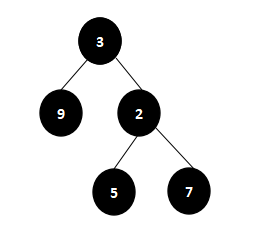
该二叉树遍历打印的结果为：[[3]，[9,2]，[5,7]]

思路同 剑指 Offer 32 - I. 从上到下打印二叉树 本题思路基本完全一致

算法流程：

1. 初始化返回列表 ret，当树的根节点为空的时候，直接返回一个空的列表

2. 初始化队列，将 root 根节点添加到队列中

3. BFS 循环

   • 首先记录队列的大小，记作 size，并初始化列表 list
   • 因为我们要保证同一层的节点在同一个列表中，所以我们要限定列表添加的元素的个数为 size 个
   • 队首元素出队，记作 root
   • 将 root.val 添加到列表中
   • 如果 root 的左（右）节点不为空，则将左（右）节点添加到队列
   • 将同一层节点的列表 list 添加到 ret 中，重新初始化列表 list，和队列当中元素个数 size

代码

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> ret = new ArrayList<>();
        if(root == null){
            return ret;
        }
        Queue<TreeNode> queue = new LinkedList<>();
        List<Integer> list = null;
        queue.offer(root);
        while(!queue.isEmpty()){
            list = new ArrayList<>();
            int size = queue.size();
            for(int i = 0; i < size; i++){
                root = queue.poll();
                list.add(root.val);
                if(root.left != null){
                    queue.offer(root.left);
                }
                if(root.right != null){
                    queue.offer(root.right);
                }
            }
            ret.add(list);
        }
        return ret;
    }
}

复杂度分析

• 时间复杂度：O(N)

我们需要将整棵树进行一次遍历，所以时间复杂度为：O(N)

• 空间复杂度：O(N)

当待遍历的树为一棵平衡二叉树时，最多有 N/2 个节点同时在队列中，所以使用 O(N) 的额外空间，这里面需要注意的是，我们初始化的列表 list 并不算做额外的使用空间，因为它也是返回值构成的一部分。