剑指 Offer 33. 二叉搜索树的后序遍历序列

解题思路：递归

示例：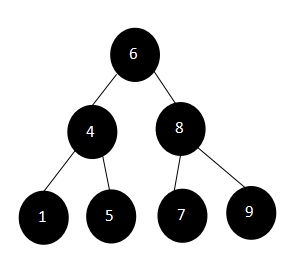
image.png
该二叉树为一棵二分搜索树

  • 前序遍历结果：[6，4，1，5，8，7，9]

  • 中序遍历结果：[1，4，5，6，7，8，9]

  • 后序遍历结果：[1，5，4，7，9，8，6]

我们可以总结二叉搜索树具有以下特点：

  1. 对于一棵二叉搜索树，任意节点的左孩子都比该节点小，右孩子都比该节点大；所以，左子树中所有节点的值均小于根节点的值，右子树中所有节点的值均大于根节点的值

  2. 二叉搜索树的中序遍历即是将该树的节点值按照从小到大排序的结果

  3. 对于一棵二叉搜索树，其任意子树也是一棵二叉搜索树

因为有特性 3 ，我们很快就能联想到使用递归的方式来解决该问题

算法流程：递归

  • 递归终止条件：子树节点数量 <= 1，直接返回 true


  • 递推过程：

    • 划分出左右子树：通过遍历后序遍历的[i,j] 区间元素，寻找第一个大于根节点的节点，其索引记作 m，我们可以划分出左子树的区间为 [i,m-1]，右子树的区间为 [m,j-1]

    • 判断是否为二叉搜索树：左子树所有的元素都应满足小于 postorder[j]，右子树所有的元素都应满足大于 postorder[j]

  • 返回值：每一个判断使用与逻辑符进行连接

    • 判断遍历到的索引最后是否走到了 j
    • recur(i,m-1) 判断左子树是否为二叉搜索树
    • recur(m,j-1) 判断右子树是否为二叉搜索树

代码

  1. class Solution {
  2.     public boolean verifyPostorder(int[] postorder) {
  3.         if(postorder == null || postorder.length == 0){
  4.             return true;
  5.         }
  6.         return verifyPostorder(postorder,0,postorder.length - 1);
  7.     }
  9.     private static boolean verifyPostorder(int[] postorder,int i,int j){
  10.         if(j <= i){
  11.             return true;
  12.         }
  13.         int p = 0; 
  14.         int m = 0;
  15.         while(postorder[p] < postorder[j]){
  16.             m++;
  17.             p++;
  18.         }
  19.         while(postorder[p] > postorder[j]){
  20.             p++;
  21.         }
  22.         return p == j 
  23.             && verifyPostorder(postorder,i,m - 1) 
  24.             && verifyPostorder(postorder,m,j - 1);
  25.     }
  26. }

复杂度分析

  • 时间复杂度：O(N²)

如果二叉搜索树退化为一个链表时，每轮递归都需要遍历树的所有节点，显然时间复杂度为 O(N²)

  • 空间复杂度：O(N)

同样的，如果二叉搜索树退化为一个链表，递归深度将达到 N，额外占用了调用栈 O(N) 的空间