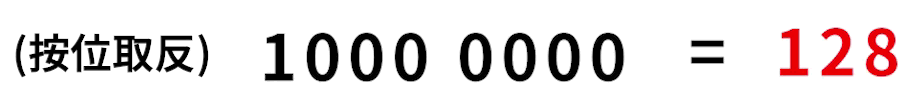有符号数

所谓有符号数就是数据有正负之分，数据无正负之分就是无符号数。
有符号数组成：符号位+数值位
最高位为符号位，0表示正数，1表示负数。

计算机中存储的是补码：
7的补码： 0b00000000 00000000 00000000 00000111

-7的原码：0b10000000 00000000 00000000 00000111
-7的反码：0b11111111 11111111 11111111 11111000
-7的补码：0b11111111 11111111 11111111 11111001

-7的补码转为原码（计算机显示给我们的是原码）
-7的补码-1 ：0b11111111 11111111 11111111 11111000
各位取反，符号位除外：0b10000000 00000000 00000000 00000000 00000111

@Test
public void test_9() {
    /**
         * -7的原码：0b10000000 00000000 00000000 00000111
         * -7的反码：0b11111111 11111111 11111111 11111000
         * -7的补码：0b11111111 11111111 11111111 11111001
         */
    System.out.println(0b10000000000000000000000000000111); //-2147483641
    System.out.println(0b11111111111111111111111111111001); // -7
}

原码 反码 补码的基本概念

原码：最高位为符号位，0代表正数，1代表负数，非符号位为该数字绝对值的二进制。
反码：正数的反码与原码一致，负数的反码是对原码按位取反，只是最高位（符号位）不变。
补码：正数的补码与原码一致，负数的补码是该数的反码加1。

计算机为什么以补码存储数据？

假设时针现在指在了3点的位置，我要让指针指向12点，那么我有两种选择（如果规定逆时针为负）
1、逆时针转3格 （-3）
2、顺时针转9格（+9）

那么，-3和+9就起到了相同的作用，二者效果一样，都是从3点到12点
那么二者有什么关系呢？
其实二者互为补码（%12） 12恰好是计数系统的容量（即钟表最多表示12个数）
那么在 %12 的情况下，9 就可以 “代替 -3” 运算
如 （8 - 3）% 12 = 5 % 12 = 5 (8 + 9) % 12 = 17 % 12 = 5
所以，补码的用处就是： 减一个数 等价于 加上这个负数的补码
那么就不用进行减法运算了，只要会加法就行，因此CPU只有加法器。

因此，补码的意义就是把负数变成它“对应的正数”，然后参与运算。

CPU只有加法器，对于减法 5-5 转换成 5+(-5)，就是5的补码加上-5的补码。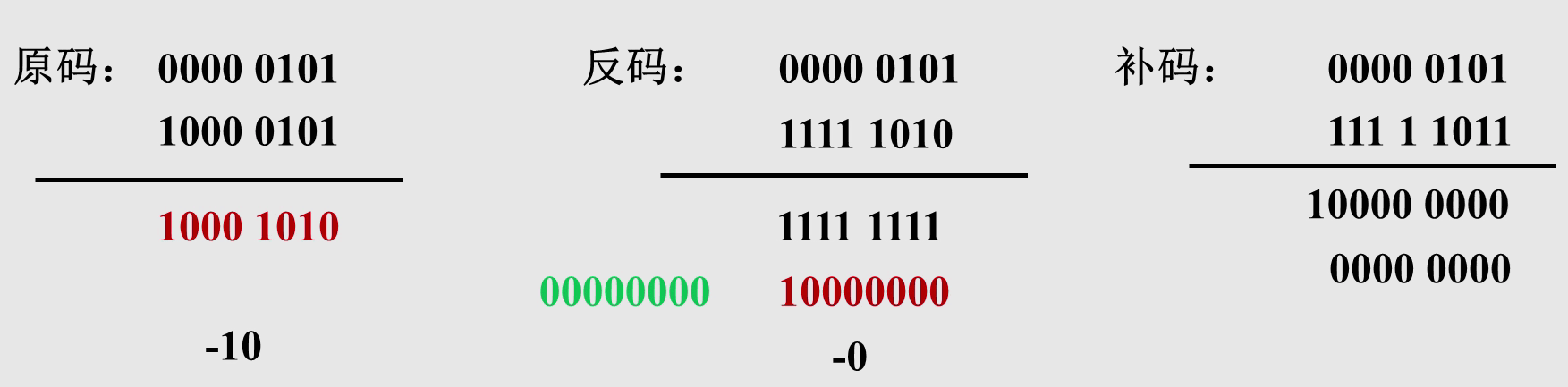

用原码相加，结果是-10， 明显结果不对。
用反码相加，结果为-0，但是 00000000 和 10000000 两个二进制数表示一个0，也是矛盾的。
用补码相加：结果为0，最高位的1会丢掉。

为何补码的符号位能参与运算？

补码根本就没有符号位， 补码就是把负数转换成正数参与运算，也就是说补码都是正数。
补码既然没有符号位（都是数值位，最高位也是），那拿最高位来运算也就是理所当然的。

补码的最高位能起到显示正负的功能（只是能起到符号位的功能），但不是真正的符号位，而是如假包换的数值位。

@Test
public void test_4() {
    byte b1 = 127;
    byte b2 = 1;
    byte b3 = 2;
    System.out.println(b1 + b2); // 128
    System.out.println((byte)(b1 + b2)); // -128
    System.out.println((byte)(b1 + b3)); // -127
}