BackTracking

回溯算法和深度优先遍历

「回溯算法」与「深度优先遍历」都有「不撞南墙不回头」的意思。我个人的理解是：「回溯算法」强调了「深度优先遍历」思想的用途，用一个 不断变化 的变量，在尝试各种可能的过程中，搜索需要的结果。强调了 回退 操作对于搜索的合理性。而「深度优先遍历」强调一种遍历的思想，与之对应的遍历思想是「广度优先遍历」
回溯算法用于搜索一个问题的所有的解，用到了DFS的思想
回溯和动态规划：
DP只需要知道最优解是什么，不关心怎么来的
回溯要列举出所有的可能性

排列问题

按顺序枚举每一位可能出现的情况，已经选择的数字在 当前 要选择的数字中不能出现。按照这种策略搜索就能够做到 不重不漏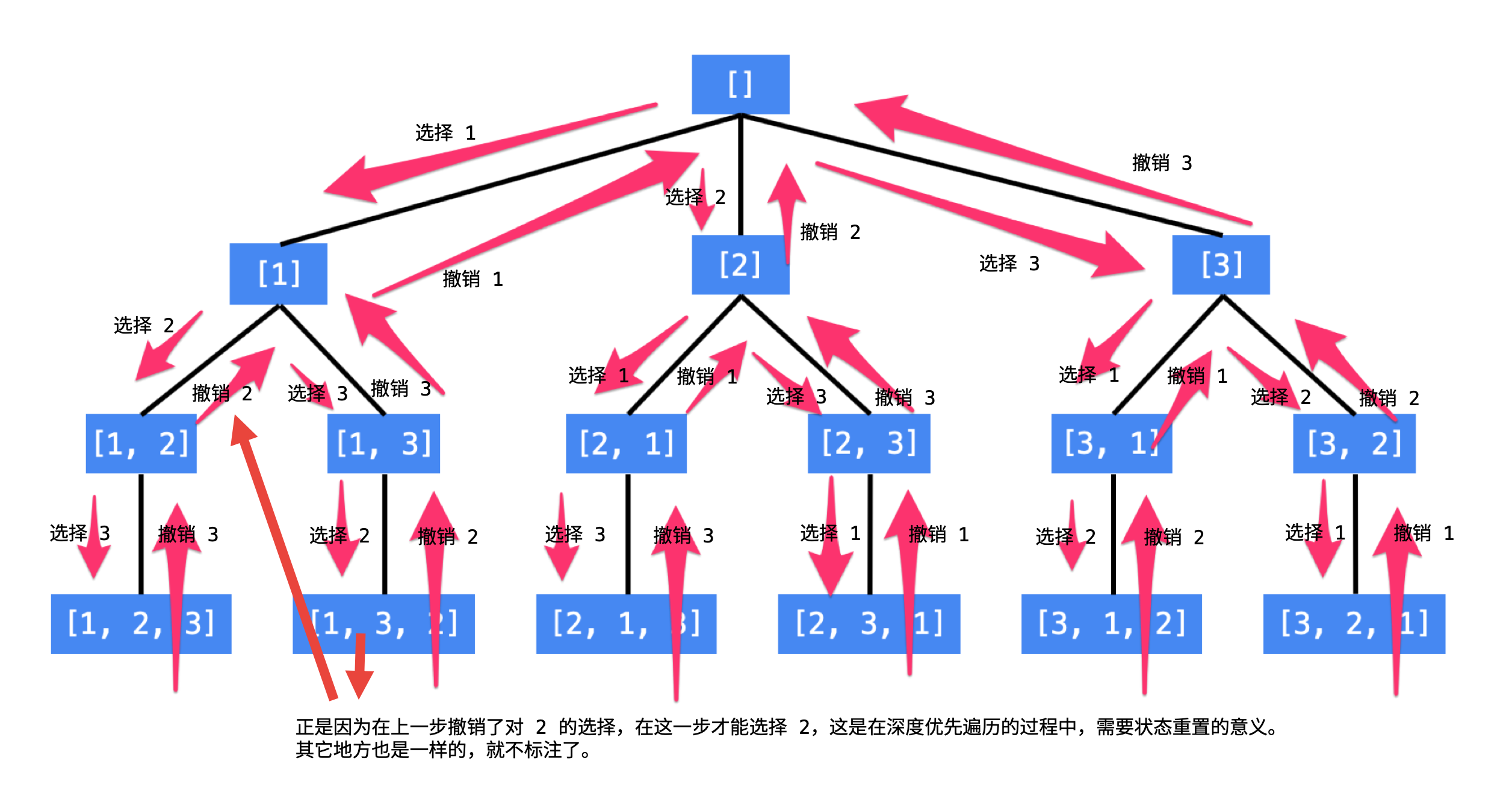

回溯和普通的DFS的区别在于，有回头的过程，且回头的时候需要把当前已经访问的节点状态重置

1. 按引用传递状态
2. 所有的状态修改在递归完成后回改

46. 全排列

https://leetcode-cn.com/problems/permutations/

        # res = []
        # def backtracking(nums, tmp):
        #     if not nums:
        #         res.append(tmp)
        #         return
        #     for i in range(len(nums)):
        #         backtracking(nums[:i]+nums[i+1:], tmp+[nums[i]])
        # backtracking(nums,[])
        # return res
        depth = len(nums)
        visited = [False for _ in range(depth)]
        res = []
        def backtracking(temp_list, height):
            if height == depth:
                res.append(temp_list)
                return
            for i in range(depth):
                if not visited[i]:
                    visited[i] = True
                    backtracking(temp_list+[nums[i]],height+1)
                    visited[i] = False
        backtracking([],0)
        return res

47. 全排列 II

https://leetcode-cn.com/problems/permutations-ii/
主要是去重的判断条件.

1. 排序, 保证相同的数字都相邻

2. 不选择的情况有:

   1. 当前元素已经visited

   2. i>0 且当前元素等于前一个元素 且 前一个元素已经被使用.

      class Solution:
      def permuteUnique(self, nums: List[int]) -> List[List[int]]:
        n = len(nums)
        if n <2:
            return [nums]
        res = []
        nums.sort()
        visited = [False for _ in range(n)]
        def backtracking(temp_list, depth):
            if depth==n:
                res.append(temp_list)
            for i in range(n):
                if visited[i] or (i>0 and nums[i]==nums[i-1] and not visited[i-1]):
                    continue
                visited[i]=True
                backtracking(temp_list+[nums[i]], depth+1)
                visited[i]=False
        backtracking([],0)
        return res

      77. 组合

      https://leetcode-cn.com/problems/combinations/

class Solution:
    def combine(self, n: int, k: int) -> List[List[int]]:
        res = []
        if k>n:
            return res
        if k == 0:
            return [res]
        def backtracking(nums,temp_list, index):
            if len(temp_list)==k:
                res.append(temp_list[:])
                return
            for i in range(index,n):
                temp_list.append(nums[i])
                backtracking(nums[index:],temp_list, i+1)
                temp_list.pop()
        nums = [i for i in range(1,n+1)]
        backtracking(nums,[],0)
        return res

39. 组合总和

https://leetcode-cn.com/problems/combination-sum/
什么时候使用 used/visited数组，什么时候使用 begin 变量

• 排列问题: 讲究顺序（即 [2, 2, 3] 与 [2, 3, 2] 视为不同列表时,需要记录哪些数字已经使用过,此时用 used 数组；
• 组合问题:不讲究顺序（即 [2, 2, 3] 与 [2, 3, 2] 视为相同列表时,需要按照某种顺序搜索,此时使用 begin 变量。

注意：具体问题应该具体分析， 理解算法的设计思想 是至关重要的，请不要死记硬背。

class Solution:
    def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
        candidates.sort()
        res = []
        length = len(candidates)
        def backtracking(temp_list, index, target):
            if target==0:
                res.append(temp_list[:])
                return
            for i in range(index, length):
                residue = target - candidates[i]
                if residue < 0:
                    break
                backtracking(temp_list+[candidates[i]], i, residue)
        backtracking([],0,target)
        return res

40. 组合总和 II

https://leetcode-cn.com/problems/combination-sum-ii/
这道题的核心相比上一题在于去重，也就是代码备注的部分
https://leetcode-cn.com/problems/combination-sum-ii/solution/hui-su-suan-fa-jian-zhi-python-dai-ma-java-dai-m-3/
参考高赞评论

class Solution:
    def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
        size = len(candidates)
        res = []
        if size<1:
            return []
        def backtracking(temp_list, begin, target):
            if target == 0:
                res.append(temp_list[:])
                return
            for i in range(begin,size):
                residue = target - candidates[i]
                if residue<0:
                    break
                #去重的核心在于这个判断
                # i>begin是为了保证同一层的第一个和上一级相同的数是允许的
                # i == i-1 是说同一层第二个及以后相同的数是不允许的    
                if i > begin and candidates[i]==candidates[i-1]:
                    continue
                backtracking(temp_list+[candidates[i]],i+1, residue)
        candidates.sort()
        backtracking([],0,target)
        return res

17. 电话号码的字母组合

https://leetcode-cn.com/problems/letter-combinations-of-a-phone-number/
难得被回溯虐了一天半之后， 自己调试出来一道回溯的题

class Solution:
    def letterCombinations(self, digits: str) -> List[str]:
        lookup = {'2':'abc','3':'def','4':'ghi','5':'jkl','6':'mno','7':'pqrs','8':'tuv','9':
        'wxyz'}
        size = len(digits)
        res = []
        if size==0:
            return []
        def backtracking(temp_list, index):
            if len(temp_list) == size:
                res.append("".join(temp_list[:]))
            # 不要试图去构建递归的整个过程，理解两层循环所对应的不同的树的层级
            for i in range(index,size): # 这一层循环对应每个数字
                panel = lookup[digits[i]] # 每个数字对应3 or 4个字母
                for j in range(len(panel)): # 这个字母里选一个
                    backtracking(temp_list+[panel[j]],i+1)
        backtracking([],0)
        return res

79. 单词搜索

https://leetcode-cn.com/problems/word-search/
一开始我按照岛屿问题的方法写，发现返回不到想要的结果。

1. line16标记，line22退回， 因为一个矩阵里，可能有多个相同的字母，有时候从一个位置出发不行，但从另一个位置出发是可以的

   class Solution:
    def exist(self, board: List[List[str]], word: str) -> bool:
        if not board:
            return False
        rows = len(board)
        cols = len(board[0])
        DIRECTION = ((1,0),(-1,0),(0,1),(0,-1))
        visited=[[False for _ in range(cols)] for _ in range(rows)]
        def inArea(x,y):
            return x>=0 and y>=0 and x<rows and y<cols
        def dfs(index,x,y):
            if index == len(word)-1:
                return board[x][y]==word[index]
            if board[x][y]==word[index]:
                visited[x][y]=True
                for k in range(4):
                    new_x = x + DIRECTION[k][0]
                    new_y = y + DIRECTION[k][1]
                    if inArea(new_x,new_y) and not visited[new_x][new_y] and dfs(index+1,new_x,new_y):
                        return True
                visited[x][y]=False
        for i in range(rows):
            for j in range(cols):
                if dfs(0,i,j):
                    return True
        return False