实现并查集类，解决连通性问题。（比如：朋友圈） 思路：把问题抽象成带有索引的数组。根据索引进行连通，从而得到连通个数。

  1. class UnionFind{
  2. private:
  3.     vector<int> parent;
  4.     vector<int> rank;
  5.     int count; // 省份个数
  6. public:
  7.     UnionFind(unsigned int size) 
  8.     {
  9.         for (int i = 0; i < size; i++) {
  10.             parent.push_back(i); // 自己的祖先是自己
  11.             rank.push_back(1);   // 圈子大小初始状态都为1
  12.         }
  13.         count = size;
  14.     }
  15.     int Find(int p)
  16.     {
  17.         while (p != parent[p]) {
  18.             // TODO:路径压缩
  19.             parent[p] = parent[parent[p]]; // 路径压缩, 可减少一倍，也可不压缩
  20.             p = parent[p];
  21.         }
  22.         return p;
  23.         // return p == parent[p] ? p : parent[p] = Find(parent[p]);
  24.     }
  25.     void UnionElement(int p, int q) 
  26.     {
  27.         int pRoot = Find(p);
  28.         int qRoot = Find(q);
  29.         if (qRoot == pRoot) {
  30.             return;
  31.         }
  32.         // 小圈子融入大圈子
  33.         if (rank[pRoot] < rank[qRoot]) {
  34.             parent[pRoot] = qRoot; // 不用维护层数
  35.         } else if (rank[pRoot] > rank[qRoot]) {
  36.             parent[qRoot] = pRoot; // 不用维护层数
  37.         } else {
  38.             parent[qRoot] = pRoot;
  39.             rank[pRoot]++; // 层数加1
  40.         }
  41.         count--;
  42.     }
  43.     int size() {
  44.         return count; // 返回圈子的个数
  45.     }
  46. };
  48. class Solution {
  49.     public:
  50.     int findCircleNum(vector<vector<int>>& isConnected) 
  51.     {
  52.         UnionFind *unionFind = new UnionFind(isConnected.size());
  54.         for (int i = 0; i < isConnected.size(); i++) {
  55.             for(int j = 0; j < isConnected[0].size(); j++) {
  56.                 if (isConnected[i][j] == 1) {
  57.                     unionFind->UnionElement(i, j);
  58.                 }
  59.             }
  60.         }
  61.         return unionFind->size();
  62.     }
  63. };

1. 题目

1631. 最小体力消耗路径

你准备参加一场远足活动。给你一个二维 rows x columns 的地图 heights ，其中 heights[row][col] 表示格子 (row, col) 的高度。一开始你在最左上角的格子 (0, 0) ，且你希望去最右下角的格子 (rows-1, columns-1) （注意下标从 0 开始编号）。你每次可以往 上，下，左，右 四个方向之一移动，你想要找到耗费 体力 最小的一条路径。
一条路径耗费的 体力值 是路径上相邻格子之间 高度差绝对值 的 最大值 决定的。
请你返回从左上角走到右下角的最小 体力消耗值 。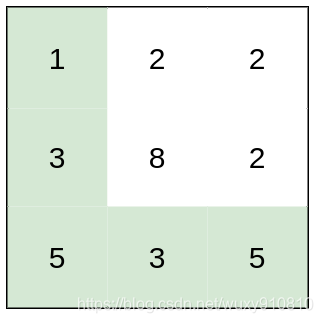
并查集 - 图1
解决思路：1、二分+BFS。2、并查集、3、二分+DFS

  1. // 并查集模板
  2. class UnionFind{
  3. private:
  4.     vector<int> parent;
  5.     vector<int> rank;
  6.     int count; // 省份个数
  7. public:
  8.     UnionFind(unsigned int size) 
  9.     {
  10.         for (int i = 0; i < size; i++) {
  11.             parent.push_back(i); // 自己的祖先是自己
  12.             rank.push_back(1);   // 圈子大小初始状态都为1
  13.         }
  14.         count = size;
  15.     }
  16.     int Find(int p)
  17.     {
  18.         while (p != parent[p]) {
  19.             // TODO:路径压缩
  20.             parent[p] = parent[parent[p]]; // 路径压缩, 可减少一倍，也可不压缩
  21.             p = parent[p];
  22.         }
  23.         return p;
  24.         // return p == parent[p] ? p : parent[p] = Find(parent[p]);
  25.     }
  26.     void UnionElement(int p, int q) 
  27.     {
  28.         int pRoot = Find(p);
  29.         int qRoot = Find(q);
  30.         if (qRoot == pRoot) {
  31.             return;
  32.         }
  33.         // 小圈子融入大圈子
  34.         if (rank[pRoot] < rank[qRoot]) {
  35.             parent[pRoot] = qRoot; // 不用维护层数
  36.         } else if (rank[pRoot] > rank[qRoot]) {
  37.             parent[qRoot] = pRoot; // 不用维护层数
  38.         } else {
  39.             parent[qRoot] = pRoot;
  40.             rank[pRoot]++; // 层数加1
  41.         }
  42.         count--;
  43.     }
  44.     int Size() {
  45.         return count; // 返回圈子的个数
  46.     }
  48.     bool Connected(int p, int q)
  49.     {
  50.         return Find(p) == Find(q);
  51.     }
  52. };
  54. class Solution {
  55. public:
  56.     static bool cmp(tuple<int, int, int>& a, tuple<int, int, int>& b)
  57.     {
  58.         return get<2>(a) < get<2>(b);
  59.     }
  61.     int minimumEffortPath(vector<vector<int>>& heights)
  62.     {
  63.         int m = heights.size();
  64.         int n = heights[0].size();
  65.         vector<tuple<int, int, int>> edges;
  67.         for (int i = 0; i < m; ++i) {
  68.             for (int j = 0; j < n; ++j) {
  69.                 int id = i * n + j; // 标记点的方式
  70.                 if (i > 0) {
  71.                     int id1 = (i - 1) * n + j; // 往上的点
  72.                     edges.emplace_back(id1, id, abs(heights[i][j] - heights[i - 1][j]));
  73.                 }
  74.                 if (j > 0) {
  75.                     int id1 = i * n + j - 1; // 往左的点
  76.                     edges.emplace_back(id1, id, abs(heights[i][j] - heights[i][j - 1]));
  77.                 }
  78.             }
  79.         }
  80.         sort(edges.begin(), edges.end(), cmp);
  82.         UnionFind uf(m * n);
  83.         int ans = 0;
  84.         for (const auto [x, y, v]: edges) {
  85.             uf.UnionElement(x, y);
  86.             if (uf.Connected(0, m * n - 1)) {
  87.                 ans = v;
  88.                 break;
  89.             }
  90.         }
  92.         return ans;
  93.     }
  94. };