1. 什么是树状数组？

  • 用数组来模拟树形结构，和Trie数的构造方式有类似之处。

    2. 应用场景？

  • 解决大部分基于区间上的更新以及求和问题。

    3. 树状数组和线段树的区别？

  • 树状数组可以解决的问题都可以用线段树解决。

  • 但树状数组的系数要小很多。

  • 具体使用哪种？优先是有树状数组，树状数组解决不了，使用线段树。

    4. 树状数组的优缺点？

  • 修改和查询的复杂度都是O(logN), 系数比线段树要少很多。

  • 复杂的区间问题，还是不能解决。

    5. 树状数组原理

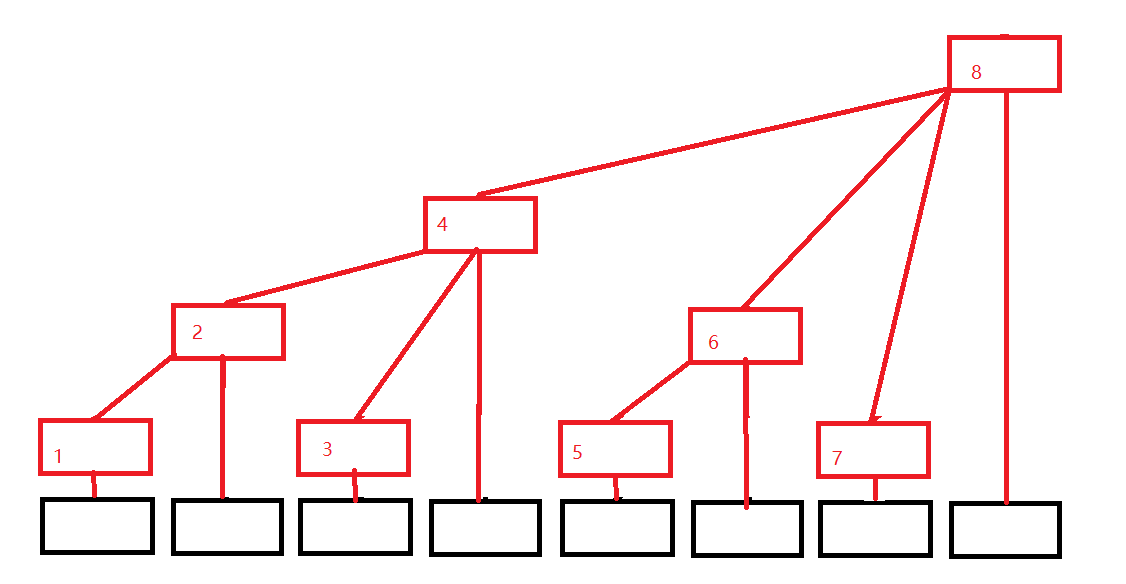
    image.png
    黑色数组代表原来的数组（下面用A[i]代替），红色结构代表我们的树状数组(下面用C[i]代替)，发现没有，每个位置只有一个方框，令每个位置存的就是子节点的值的和，则有

  • C[1] = A[1];

  • C[2] = A[1] + A[2];
  • C[3] = A[3];
  • C[4] = A[1] + A[2] + A[3] + A[4];
  • C[5] = A[5];
  • C[6] = A[5] + A[6];
  • C[7] = A[7];
  • C[8] = A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8];

可以发现，这颗树是有规律的
树状数组 - 图2
// k为i的二进制中从最低位到高位连续零的长度
例如i = 8(1000)时候，k = 3，可自行验证。

区间求和：
比如我们要找前7项和，那么应该是sum[7] = C[7] + C[6] + C[4];
得到公式：
**sum[i] = C[i] + C[i-2^k1] + C[(i-2^k1)-2^k2] + .....；**
树状数组就是一个二进制上面的应用。
i位置上对应的2^k = i & (-i); // 求解2^k，有个专门的名词lowbit。

6. 树状数组代码模板

  1. vector<int> num(n); // 原数组
  2. vector<int> tree(n + 1); // 注意树状树状是从1开始的
  3. int n;
  5. // 求2^k次
  6. int lowbit(int num) {
  7.     return (num & (-num));
  8. }
  9. // 求A[1] 到 A[index]的和
  10. int getSum(int index) { 
  11.     int sum = 0;
  12.     for (int i = index; i > 0; i -= lowbit(i)) {
  13.         sum += tree[i];
  14.     }
  15.     return sum;
  16. }
  18. // C[i] = A[i - 2^k + 1] + A[i - 2^k + 2] + ... + A[i];
  19. // 那么如果我们更新某个A[i]的值，则会影响到所有包含有A[i]位置。如果求A[i]包含哪些位置里呢，同理有A[i] 包含于 C[i + 2^k]、C[(i + 2^k) + 2^k]...；
  20. // 在index位置上加个val
  21. void add(int index, int val) { 
  22.     for (int i = index; i <= n; i += lowbit(i)) {
  23.         tree[i] += val;
  24.     }
  25. }

7. eg. 单点更新，求区间和

  1. class NumArray {
  2. public:
  3.     vector<int> nums; // 原数组
  4.     vector<int> tree; // 注意树状树状是从1开始的
  5.     int n;
  7.     // 求2^k次
  8.     int lowbit(int num) {
  9.         return (num & (-num));
  10.     }
  11.     // 求A[1] 到 A[index]的和
  12.     int getSum(int index) { 
  13.         int sum = 0;
  14.         for (int i = index; i > 0; i -= lowbit(i)) {
  15.             sum += tree[i];
  16.         }
  17.         return sum;
  18.     }
  19.     // 在index位置上加个val
  20.     void add(int index, int val) { 
  21.         for (int i = index; i <= n; i += lowbit(i)) {
  22.             tree[i] += val;
  23.         }
  24.     }
  26.     NumArray(vector<int>& nums) {
  27.         n = nums.size();
  28.         tree.resize(n + 1);
  29.         this->nums = nums;
  30.         for (int i = 0; i < n; i++) {
  31.             add(i + 1, nums[i]);
  32.         }
  33.     }
  35.     void update(int index, int val) {
  36.         add(index + 1, val - nums[index]);
  37.         nums[index] = val;
  38.     }
  40.     int sumRange(int left, int right) {
  41.         return getSum(right + 1) - getSum(left);
  42.     }
  43. };