L1480 动态数组求和

20210325

题目

  1. 你一个数组 nums 。数组「动态和」的计算公式为：runningSum[i] = sum(nums[0]…nums[i]) 。
  3. 请返回 nums 的动态和。
  7. 示例 1：
  9. 输入：nums = [1,2,3,4]
  10. 输出：[1,3,6,10]
  11. 解释：动态和计算过程为 [1, 1+2, 1+2+3, 1+2+3+4] 。
  12. 示例 2：
  14. 输入：nums = [1,1,1,1,1]
  15. 输出：[1,2,3,4,5]
  16. 解释：动态和计算过程为 [1, 1+1, 1+1+1, 1+1+1+1, 1+1+1+1+1] 。
  17. 示例 3：
  19. 输入：nums = [3,1,2,10,1]
  20. 输出：[3,4,6,16,17]
  23. 提示：
  25. 1 <= nums.length <= 1000
  26. -10^6 <= nums[i] <= 10^6
  28. 来源：力扣（LeetCode）
  29. 链接：https://leetcode-cn.com/problems/running-sum-of-1d-array
  30. 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

我的思路

题被我写残疾了，原意是外层遍历控制循环次数，内层用前n项和公式求阶乘，奈何Sn没有写出来，阶乘的方法是用python写的，迁移不过来，另外代码我也忘记了。做了一个半成品，但目前三月底，进度不能再拖了。

再看第二遍的时候我发现自己的解题方法错了，Sn前n项和适用于递增自然数数列，而这里数组中的每一个元素可以相同也可以不同；
image.png

过程

1，应该先创建动态数组再进行赋值替换；
2，对数组的声明使用指针的格式；
3，返回值也是一个数组，是否需要解引用运算符？是否需要回收内存？
image.png

正确解法

  1. /**
  2.  * Note: The returned array must be malloced, assume caller calls free().
  3.  */
  4. int* runningSum(int* nums, int numsSize, int* returnSize){
  5.     // 这个函数是一个数组，参数分别为原来的数组，数组大小（一个常量），返回值为修改后的数组
  6.     int* res = (int*)malloc(numsSize * sizeof(int));  // 谁作为动态分配的数量？
  7.     *returnSize = numsSize;
  8.     res[0] = nums[0];  // 应有判断为空的情况
  9.     for (int a = 1; a < numsSize; a++)
  10.     {
  11.         res[a] = res[a-1] + nums[a];
  12.     }
  13.     return res;
  14. }

做这个题，有两个要素影响成败。

第一个是读题，题目已经给定了函数原型，程序员知道如何给函数传递参数，更为重要的一个参数是numsSize&returnSize,一个限定了数组的长度，另外一个则限定了函数返回数组的长度；

第二个是分配内存的语法，为了一致性，会强制转换数组的数据类型，其次由于动态分配内存，所以数组的长度肯定要与一个变量构建关系，数组元素的长度直接取决于数据类型的长度；

在经典教材中，还需要释放内存；

其他解法

前一个解法是原数组和现在新的数组错位相加，这一个解法是累加；

先动态分配内存空间，设定一个收集器，统计上一次运算得出的值；

初始化一个变量，变量用来做for循环的条件，控制循环的次数；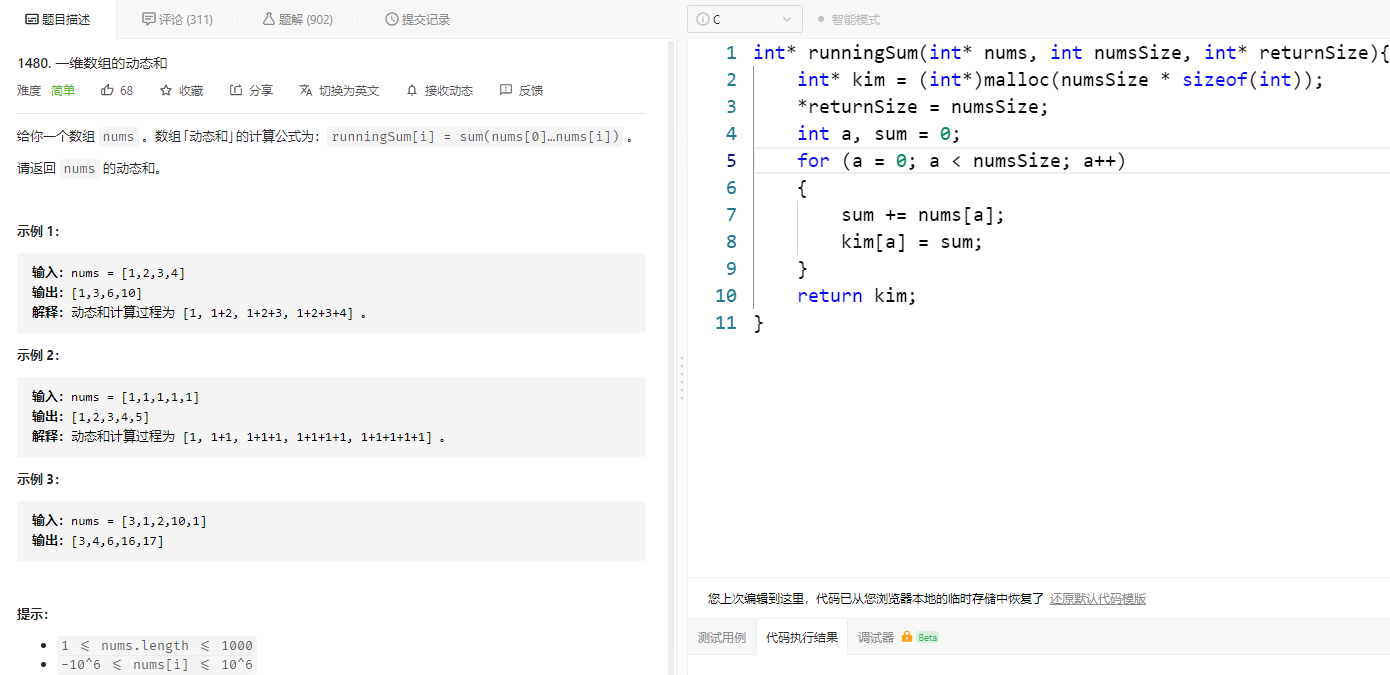
image.png

第三种解法

由于计算前后的数组，第一个元素完全一样，所以直接计算从第一个元素开始运算和填充，这个解题思路，存储值的时候不需要额外存储空间，是一种原地运算和填充；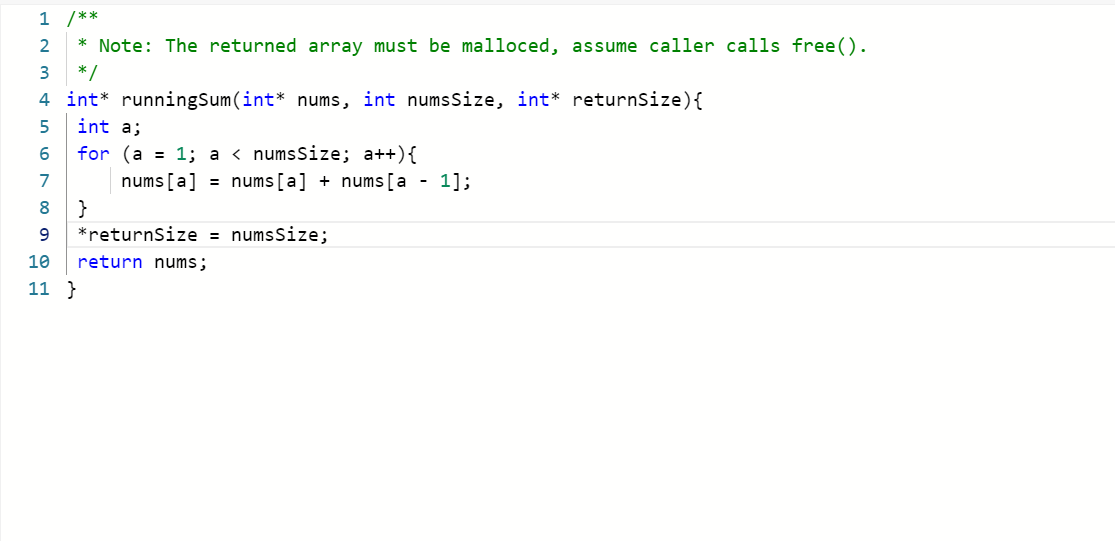
image.png

外部引用

经典教材中对于内存分配与回收知识点的补充：主要收获是如何分配动态内存空间，以及回收内存。简单地讲，指针是一个沟通媒介。

  1. /*dyn_arr.c -- 动态分配数组*/
  2. //20210326  11：27
  3. #include <stdio.h>
  4. #include <stdlib.h>  /*为malloc() & free()函数提供原型*/
  6. int main(void)
  7. {
  8.     double* ptd;  /*指针变量*/
  9.     int max;
  10.     int number;
  11.     int i = 0;
  12.     puts("What is the maximum number of type double entries?");  /*约束数组的长度：双精度浮点数有几个？*/
  13.     if (scanf_s("%d", &max) != 1)  /*非数字字符即为零，确保输入为数字字符才有意义*/ 
  14.     {
  15.         puts("Number not correctly entered -- bye.");
  16.         exit(EXIT_FAILURE);
  17.     }
  18.     ptd = (double*)malloc(max * sizeof(double));  /*double*:是强制数据类型转换，创建可以动态分配的数组空间，防止创建失败，没有空间存储数据*/
  19. // ptd接受的是数组内存地址
  20.     if (ptd == NULL)
  21.     {
  22.         puts("Memory allocation failed. Goodbye.");
  23.         exit(EXIT_FAILURE);/*malloc分配内存不成功则返回空指针*/
  24.     }
  25.     /*ptd现在指向有max个元素的数组*/
  26.     puts("Enter the value(q to quit):");
  27.     while (i < max && scanf_s("%lf", &ptd[i]) == 1)  /*max的值就是数组长度的最大值，并且要求填充数组的元素必须是数字*/
  28.         ++i;  /*先运算，后赋值*/
  29.     printf("Here are your %d entries:\n", number = i);  /*输入完成之后再答应这句话，展示所有的输入值，i是一个计数器，最后一个元素完成输入之后的计数*/
  30.     for (i = 0; i < number; i++)  /*条件语句中，对i初始化（说明可以局部初始化不影响运算），i还是需要自增减，条件是小于数组的元素个数*/
  31.     {
  32.         printf("%7.2f", ptd[i]);  /*循环打印结果，字符宽度为7，精度为2，打印数组中的每一个元素*/
  33.         if (i % 7 == 6)
  34.           putchar("\n");  // 用于换行
  35.     }
  36.     if (i % 7 != 0)
  37.       putchar("\n");  // 用于换行
  38.     puts("Done.");
  39.     free(ptd);
  41.     return 0;
  42. }

image.png
数组长度在参数传递中失真

Leecode1413

20210410

题目

  1. 1413. 逐步求和得到正数的最小值
  2. 给你一个整数数组 nums 。你可以选定任意的 正数 startValue 作为初始值。
  4. 你需要从左到右遍历 nums 数组，并将 startValue 依次累加上 nums 数组中的值。
  6. 请你在确保累加和始终大于等于 1 的前提下，选出一个最小的 正数 作为 startValue 。
  10. 示例 1：
  12. 输入：nums = [-3,2,-3,4,2]
  13. 输出：5
  14. 解释：如果你选择 startValue = 4，在第三次累加时，和小于 1 。
  15.                 累加求和
  16.                 startValue = 4 | startValue = 5 | nums
  17.                   (4 -3 ) = 1  | (5 -3 ) = 2    |  -3
  18.                   (1 +2 ) = 3  | (2 +2 ) = 4    |   2
  19.                   (3 -3 ) = 0  | (4 -3 ) = 1    |  -3
  20.                   (0 +4 ) = 4  | (1 +4 ) = 5    |   4
  21.                   (4 +2 ) = 6  | (5 +2 ) = 7    |   2
  22. 示例 2：
  24. 输入：nums = [1,2]
  25. 输出：1
  26. 解释：最小的 startValue 需要是正数。
  27. 示例 3：
  29. 输入：nums = [1,-2,-3]
  30. 输出：5
  33. 提示：
  35. 1 <= nums.length <= 100
  36. -100 <= nums[i] <= 100
  37. 通过次数8,815提交次数12,836

原本的思路

我的理解是，选取的最小正数和累加对象都是数组中的元素，另外每次累加和我希望通过while语句，验证后存储到列表当中。

这里面的误解就是，最小整数是随机正数，最开始想是不是最小正数和数组之间存在某种计算关系？所以我就在想是不是使用随机函数获取最小正数？

验证每次累加和的时候，最初的想法是使用所有元素求和，但是和会掩盖负数的存在，所以这种计算方法并不可取！！！

唯一思考比较正确的是，可以使用内建函数min求取最小值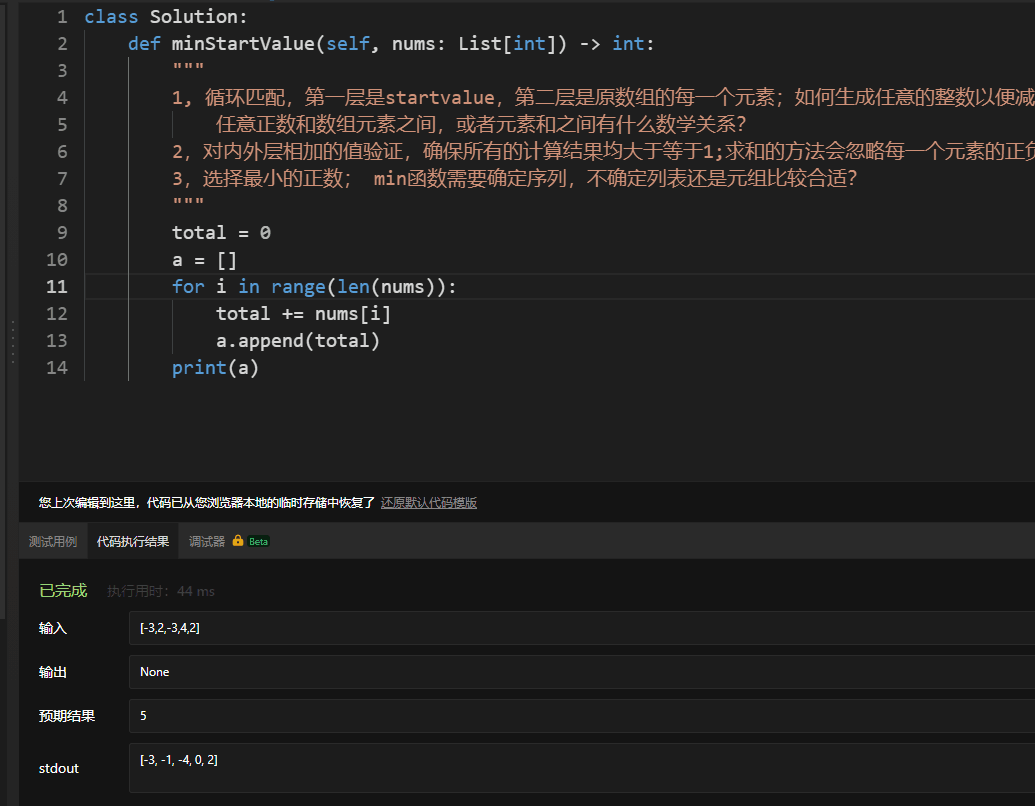
1413求解过程.png

正确的解题思路

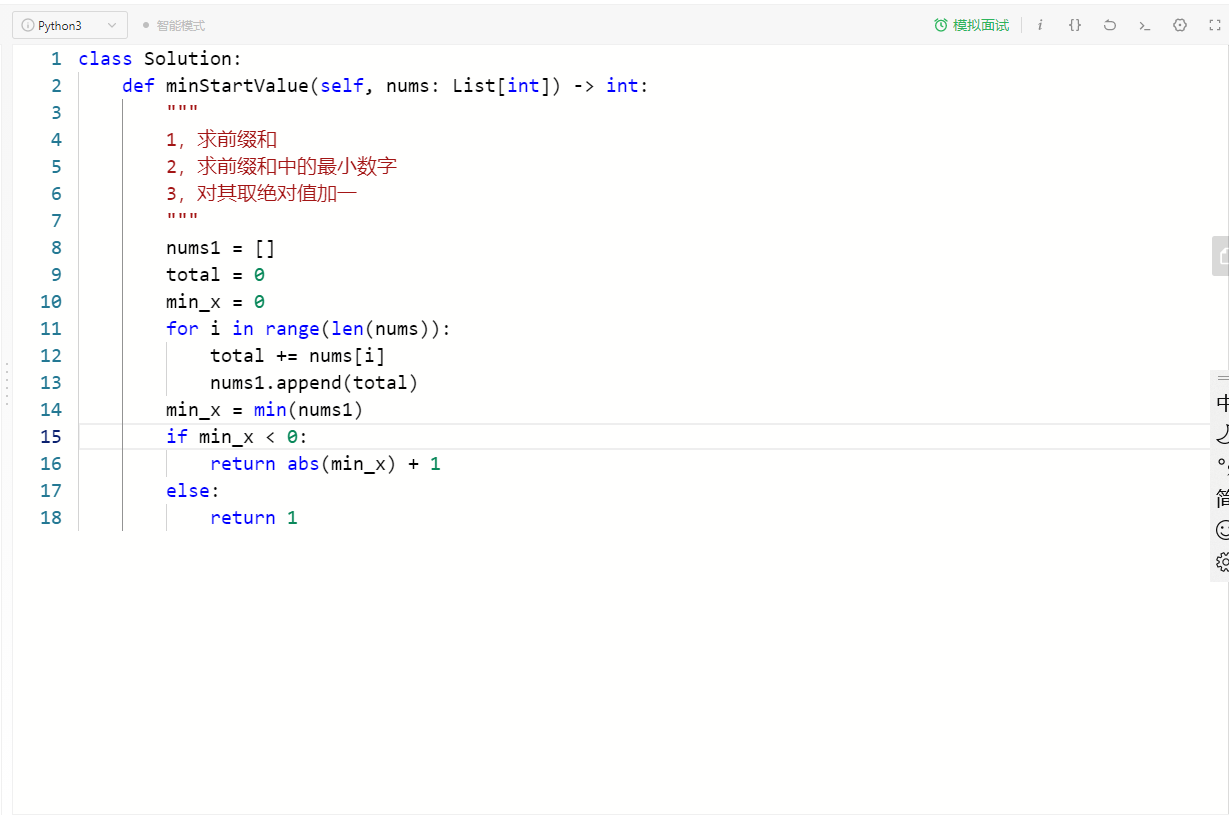
处理累加，使用的是前缀和，简单的说，前缀和就是使用索引值标定相加的元素，前缀和数组中的每一个元素，都是前一个前n+1元素的和，索引值为0的元素前后一致；
image.png

我们把startvalue与数组的累加，转变为startvalue与前缀和元素分别相加；

最小正数与原来数组的关系，被转换为求取前缀和中元素的最小值，如果为负数，我们的解决思路是直接求取绝对值并且加一，因为我们需要每一个元素和我们startvalue相加的值均大于1。此外，如果最小值大于或者等于零，我们直接返回最小正数：1；

image.png

C语言版本

解题思路

和python版本的解题思路一致，语言不同，实现方法略有差异

使用循环遍历，求取前缀和，然后取得最小值，计算后得出最小整数

关键点

变量初始化的时候一定要赋值；

设定数组长度，也就是遍历的深度的时候，综合考虑运算符的区别，比如大于和大于等于。因为人的计数方式和计算机的索引计数方式的标的不一样；

最小值求取中，比较的对象应该是数组中的值，一般设定为数组的第零个元素；

if else语句，如果在花括号之后写了分号，那么两个语句就自然隔断，并且else后面无须冒号
image.png

Leecode02两数之和

第一个版本

解题思路：
通过遍历，与每一次遍历到的元素做差，从遍历的那个元素开始截断整个数组并且保存在一个临时空间，对其遍历，找到满足要求的差值，第二次遍历是在另外一个数组，起始点就是next_index指针，所以即使找到了做差后的数字，在返回其索引值时，在临时结点值的基础上再加上起始点next_index的值

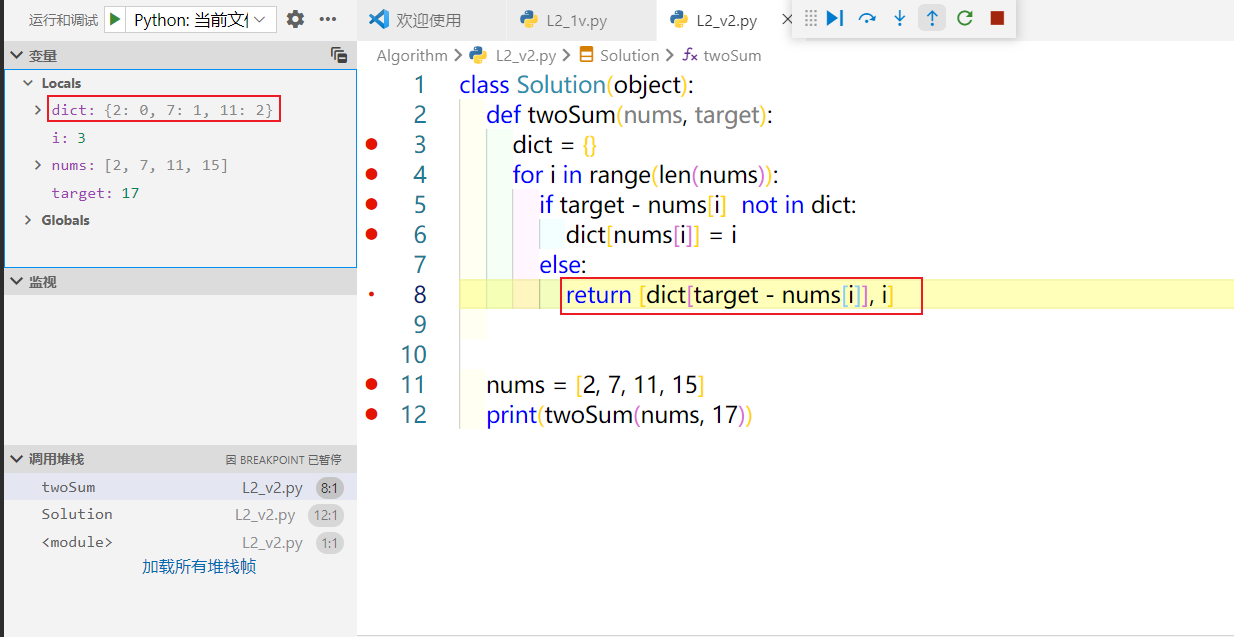
  1. class Solution:
  2.     def twoSum(self, nums: List[int], target: int) -> List[int]:
  3.         for i in nums:
  4.             j = target - i
  5.             start_index = nums.index(i)
  6.             next_index = start_index + 1
  7.             temp_nums = nums[next_index:]
  8.             if j in temp_nums:
  9.                 return (nums.index(i), next_index + temp_nums.index(j))

由调试过程可知，该解决方案其实将求解过程分解为两个部分，首先以首元素为基，对其做差，然后在首元素以后的任何元素组成的数组中寻找差值，最终还原求得位序。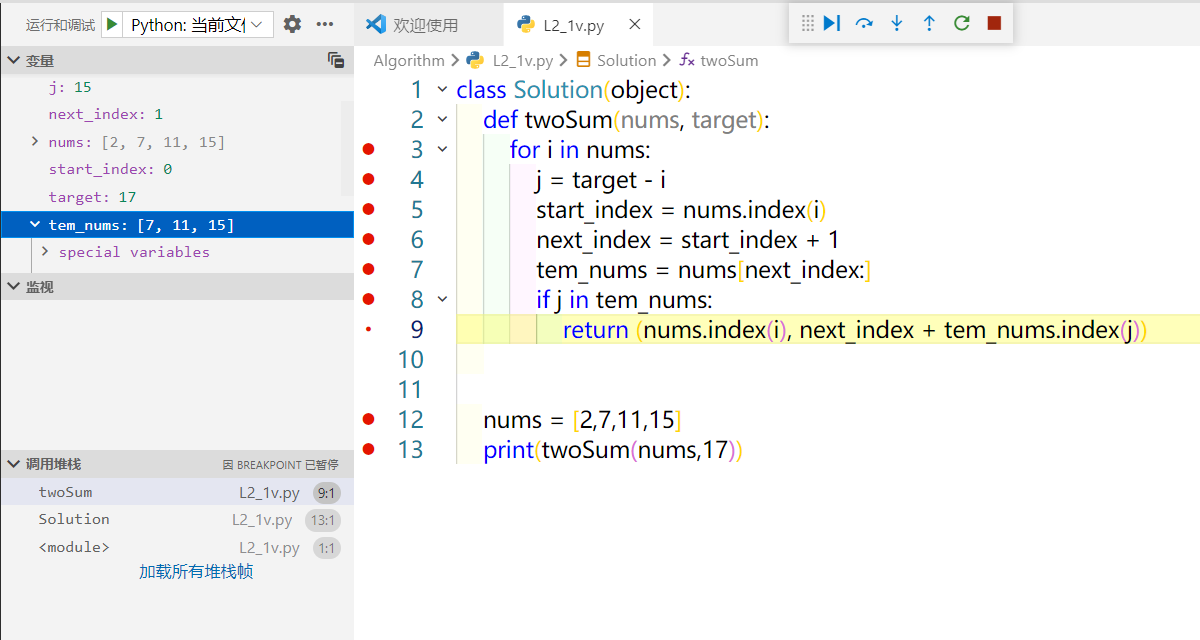
image.png
第二个版本
解题思路：
同上，还是固定第一个元素，然后创建临时空间，将所有元素和位序存储在字典里面，在元素不重复的情况下，继续遍历后面的数字，如果得到差，那么直接返回的当前遍历的数字和首元素的位序。但可以看出，这两种方法的时空复杂度都是最差的；

  1. class Solution:
  2.     def twoSum(self, nums: List[int], target: int) -> List[int]:
  3.         dict = {}
  4.         for i in range(len(nums)):
  5.             if target - nums[i] not in dict:
  6.                 dict[nums[i]] = i
  7.             else:
  8.                 return [dict[target - nums[i]], i]

image.png

LeeCode1094 拼车

题目

  1. 假设你是一位顺风车司机，车上最初有 capacity 个空座位可以用来载客。由于道路的限制，车 只能 向一个方向行驶（也就是说，不允许掉头或改变方向，你可以将其想象为一个向量）。
  3. 这儿有一份乘客行程计划表 trips[][]，其中 trips[i] = [num_passengers, start_location, end_location] 包含了第 i 组乘客的行程信息：
  5. 必须接送的乘客数量；
  6. 乘客的上车地点；
  7. 以及乘客的下车地点。
  8. 这些给出的地点位置是从你的 初始 出发位置向前行驶到这些地点所需的距离（它们一定在你的行驶方向上）。
  10. 请你根据给出的行程计划表和车子的座位数，来判断你的车是否可以顺利完成接送所有乘客的任务（当且仅当你可以在所有给定的行程中接送所有乘客时，返回 true，否则请返回 false）。
  14. 示例 1：
  16. 输入：trips = [[2,1,5],[3,3,7]], capacity = 4
  17. 输出：false
  18. 示例 2：
  20. 输入：trips = [[2,1,5],[3,3,7]], capacity = 5
  21. 输出：true
  22. 示例 3：
  24. 输入：trips = [[2,1,5],[3,5,7]], capacity = 3
  25. 输出：true
  26. 示例 4：
  28. 输入：trips = [[3,2,7],[3,7,9],[8,3,9]], capacity = 11
  29. 输出：true
  32. 提示：
  34. 你可以假设乘客会自觉遵守 “先下后上” 的良好素质
  35. trips.length <= 1000
  36. trips[i].length == 3
  37. 1 <= trips[i][0] <= 100
  38. 0 <= trips[i][1] < trips[i][2] <= 1000
  39. 1 <= capacity <= 100000
  41. 来源：力扣（LeetCode）
  42. 链接：https://leetcode-cn.com/problems/car-pooling
  43. 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

第一个版本

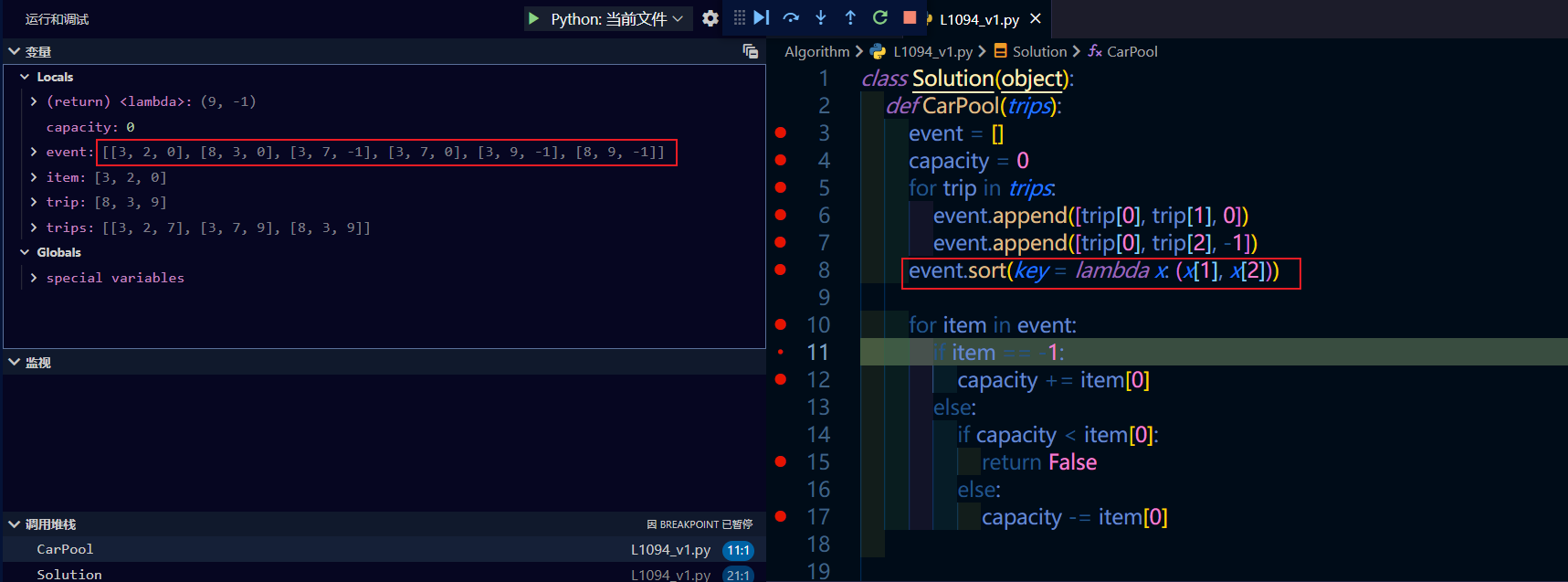
  1. class Solution(object):
  2.     def CarPool(trips):
  3.         event = []
  4.         capacity = 0  # 表示可以容纳的人数，初始值为1，即满座
  5.         for trip in trips:  # 对二维数组遍历 ，提取第二层数组
  6.             event.append([trip[0], trip[1], 0])  # 将一个数组中的上下车过程整理为两个数组，分别表示上下车，同时增加一个标志位表示对人数的操作，下车就得减一
  7.             event.append([trip[0], trip[2], -1])
  8.         event.sort(key = lambda x: (x[1], x[2]))  # 使用临时函数表达作为关键字对整理后的数组进行排序，其中第一个关键字排序指的是上下车地点，第二个关键字是容量加减
  9.         # 排序后的值： [[3, 2, 0], [8, 3, 0], [3, 7, -1], [3, 7, 0], [3, 9, -1], [8, 9, -1]]
  11.         for item in event:
  12.             if item == -1:
  13.                 capacity += item[0]  # 该处执行的是下车操作，一旦下车就会加上第二个数组的人数
  14.             else:
  15.                 if capacity < item[0]:  # 如果车上的座位不足，即capacity小于即将上车的人数，那么则拒绝上车
  16.                     return False
  17.                 else:
  18.                     capacity -= item[0]  # 如果当前容量大于等于待上车人数，那么就可以上车
  20.         return True
  22.     trips = [[3,2,7],[3,7,9],[8,3,9]]
  23.     print(CarPool(trips))

第七行代码的排序结果

image.png

LeeCode628 三个数字的最大乘积

题目

  1. 给你一个整型数组 nums ，在数组中找出由三个数组成的最大乘积，并输出这个乘积。
  5. 示例 1：
  7. 输入：nums = [1,2,3]
  8. 输出：6
  9. 示例 2：
  11. 输入：nums = [1,2,3,4]
  12. 输出：24
  13. 示例 3：
  15. 输入：nums = [-1,-2,-3]
  16. 输出：-6
  19. 提示：
  21. 3 <= nums.length <= 104
  22. -1000 <= nums[i] <= 1000
  23. 通过次数72,747提交次数139,209
  25. 来源：力扣（LeetCode）
  26. 链接：https://leetcode-cn.com/problems/maximum-product-of-three-numbers
  27. 著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

第一个版本

  1. class Solution(object):
  2.     def MaxProduct(nums):
  3.         nums.sort()
  4.         if nums[0] >= 0 or nums[-1] < 0:  # 当最小的元素大于零，或者最大的元素小于零时，都从右到左取三个数字
  5.             return (nums[-3] * nums[-2] * nums[-1])
  6.         return max(nums[-1] * nums[0] * nums[1], nums[-3] * nums[-2] * nums[-1])  # 当元素同时存在大于零和小于零的元素时，让数组最大的连续三个数字相乘，或者最大值和最小值相乘，再找一个次于最小值的数字相乘，这样可以保证绝对值一致
  9.     nums = [-5, -3, 0, 9, 8, 6]
  10.     print(MaxProduct(nums))