Applied Perception课堂笔记：视觉通道的可表达性(Expressiveness)与有效性(Effectiveness)

在可视化设计或者自动 encoding 算法的设计时，如何产出效果更好的可视化图表是一个非常有趣的话题。诸如 voyager、tableau 等可视化应用中，都基于视觉通道的可表达性 (Expressiveness) 与有效性 (Effectiveness) 来设计图表推荐规则。本文基于学习 NYU 公开课 Applied Perception 时的课堂笔记以及相关领域的论文，介绍视觉通道的可表达性与有有效性如何影响可视化设计与图表推荐。

1. 视觉通道的可表达性 (Expressiveness)

Type of infomation that can (or cannot) be expressed with a channel.

视觉通道的可表达性主要研究什么某个视觉通道能够表达哪些数据类型。常见的视觉通道可以参考图 1-1

图 1-1 常见的视觉通道

通常的数据类型可以根据标度类型划分为以下四种 (Steven, 1946):

• 名词类型 (nominal)：一般的类别类型变量
• 顺序类型 (ordinal)：可以拥有顺序含义的类别类型变量，如排名
• 区间类型 (interval)：可以做加减法，但除法或比值没有意义。如温度，日期 (有时日期也可以简化为顺序类型，这时只关心先后不关心间隔)。区间类型不存在绝对意义上的 0 点。
• 比值类型 (ratio)：可以做比值的变量，如质量、速率等。

在实际应用中，可以使用简化的版本，将区间类型与比值类型当做数值类型来处理。

在表达数值类型的变量时主要使用的通道有：position, size, angle, slope, density 等

表达顺序时基本上用于表达数值类型的通道都可以被使用，但是有一些数值类型的通道在表达顺序时会带来一些误导 (如大小)，让读者误以为这些通道是在表达一个具体的数值。避免这种误导的一种有效方法是使用一些在表达数值能力上没有那么强的变量，如文字、密度、透明度等。

表达类别类型的时主要使用的通道有：position, color hue(色相), 形状

2. 视觉通道的有效性 (Effectiveness)

Effectiveness is about how well a given channel can represent certain type of information.

衡量视觉通道的有效性可以从通道的多个性质上来描述：

• 准确度 Accuracy
• 区分度 Discriminability
• 显著性 Salience
• 可分性 Separability
• 分组 Grouping

2.1 准确度 (Accuracy)

准确度是用来描述一个通道对数值型的变量表达的准确程度。对于准确度早期较为系统的研究是来源于 Gustav Fechner 创立的 phychophysics(Fechner et al. 1966)。

Phychophysics 中一个很重要的内容是研究信号实际的物理强度与人感知到的强度之间的关系，通过一系列实验: 让参与者描述一个信号变大了多少 (如估计两次亮度之间差的大致倍数)，并对比实际变化量来描述一个具体的通道类型。

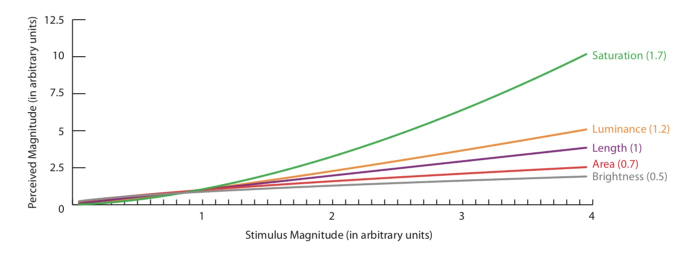
图 2-1 - Stevens’s Power Law (Maguire, 2014)

如图 2-1 所示，研究发现信号的物理强度与人感知的强度总是会满足幂律分布
(φ(I) 为感知到的数值，I 为实际的物理数值，a 取决于具体的通道)(Stevens, 1970)。

具体到可视化研究领域，对于不同视觉通道的准确度的研究可以参考 Cleveland 和 McGill 的研究 (Cleveland & McGill, 1984)。

图 2-2 不同种类型的 position/length 的准确度的研究 (Cleveland & McGill, 1984)

图 2-2 中，实验让参与者估计被标注的柱子的大小比，然后将估计值与实际值进行对比，来研究在不同图表中的数据表达准确度的差异。其中 Type 1-3 是对比 position(因为矩形是沿 x 轴对齐的)，而在 Type4-5 中，由于矩形没有对齐的对象、人眼在比较时是对比 length。

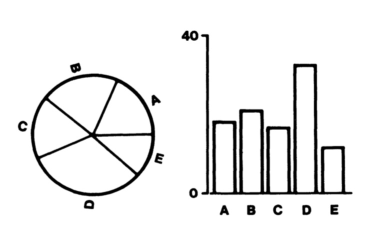
图 2-3 angle 与 position 的准确度对比 (Cleveland & McGill, 1984)

图 2-3 中，则是让实验参与者在饼图与柱状图中估计每一个类别与最大类别的数量比值。这种设计可以让人眼专注于数值准确度的比较而不会去参考自己记忆中的一些数值占比的饼图形状 (因为不同人员的经验可能不同，要尽可能排除这种因素的干扰)。

最终的实验结果如下

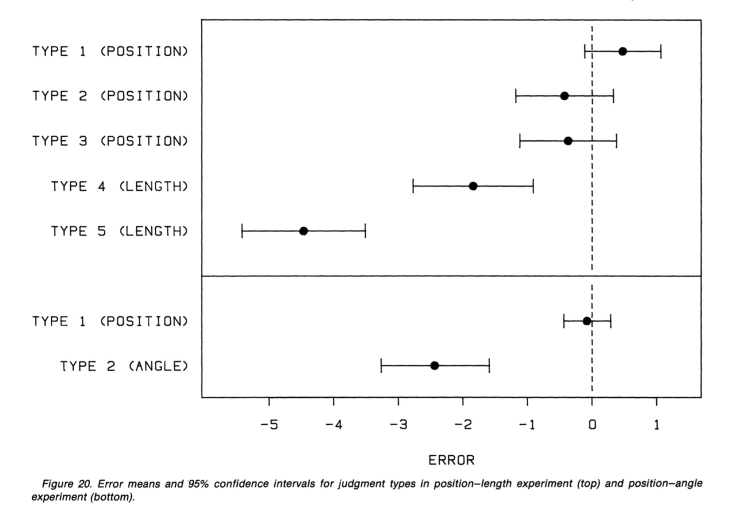
图 2-4 Cleveland&McGill 试验结果 (Cleveland & McGill, 1984)

可以看出大致的视觉通道表达准确度的优先级: Position > Length > Angle。值得注意的是，在堆叠柱状图的场景下，估计同一个堆叠组内的矩形长度比误差是要高于饼图的 (Type-5)，但估计两个不同堆叠组中同类别的矩形的长度比是要高于饼图。所以堆叠柱状图的横向比较能力要强于饼图，纵向比较能力却若于饼图。在可视化自动 encoding 算法设计时，不能盲目的将 length 的优先级排在 angle 之前，尽量要参考需要比较的对象（这就需要判断用户的分析意图）。

后续 Heer 与 Bostock 复现了此实验并在此基础上增加了更多的视觉通道类型 (Heer & Bostock, 2010)，实验结果如图 2-5 所示

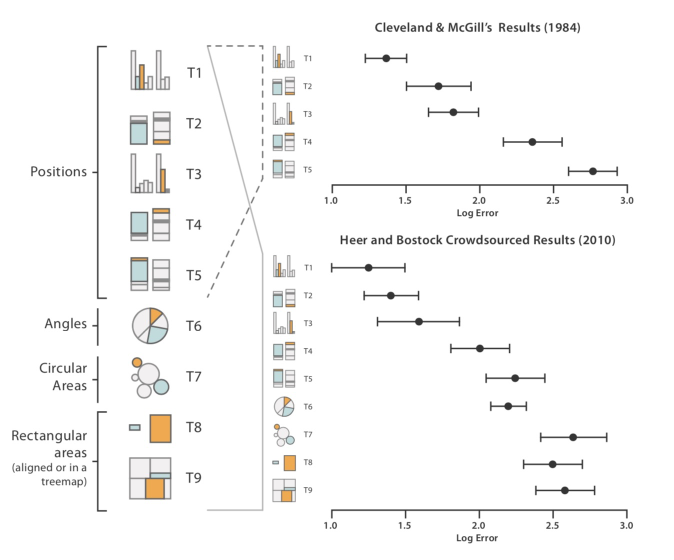
图 2-5 视觉通道表达准确度实验结果 (Maguire, 2014)

图 2-6 不同的视觉通道对不同类别变量的表达准确程度 (Maguire, 2014)

图 2-6 中对于 Quantitative 的准确度研究是已经经过试验验证过的，而 Ordinal 与 Categoricak 类型是 Mackinlay 基于一些已有的 phychophysics 推论出来的，但尚未经过实验的验证 (Mackinlay, 1986)。

实践案例

以 kaggle 上的Video Game Sales数据集为例

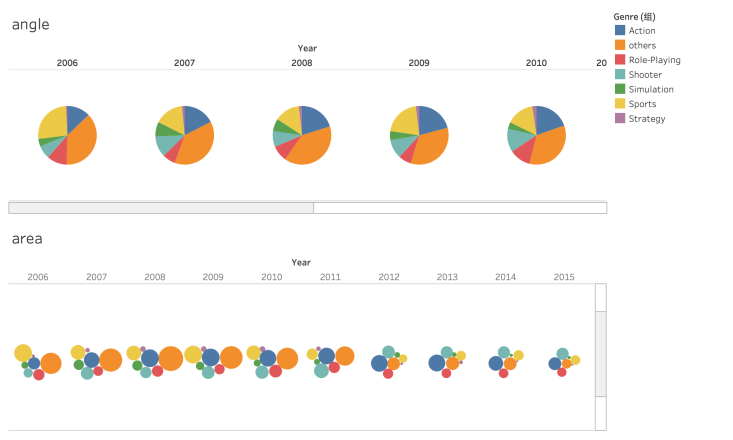
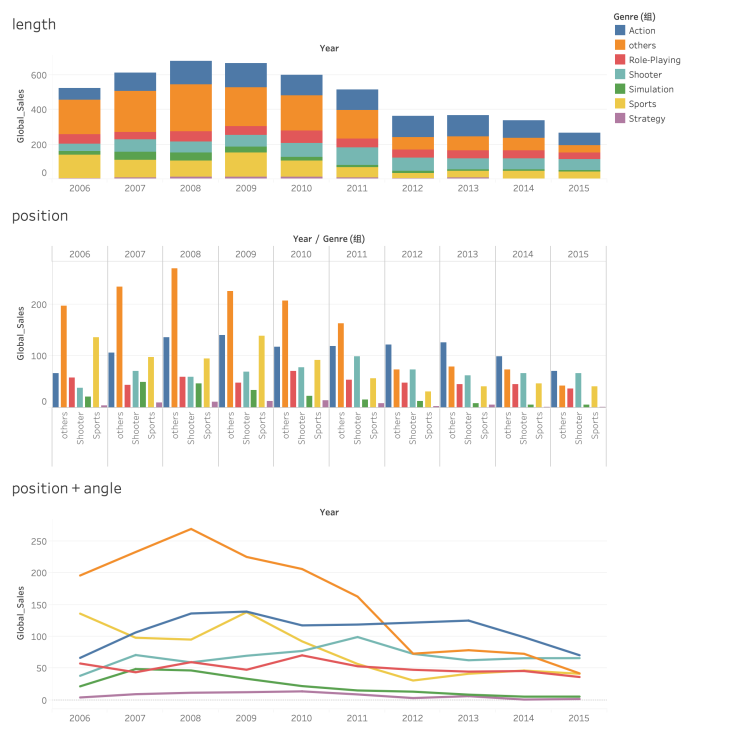
对比分组柱状图与堆叠柱状图，堆叠柱状图由于很多分类没有进行对齐，所以其本质上是在使用 length 通道，而分组柱状图所有的矩形都基于横轴对齐，所以对比时使用了 position 通道，由此在比较每一个子分类在不同年的相对大小时，分组柱状图表达的准确度要高于堆叠柱状图。

相比于分组柱状图中只是用了 position 对数量的描述，折线图中除了使用了 position 通道表达了销量之外，折现拐点对应的 angle 通道还可以表达变化率，而柱状图中变化率则并没有通道对其进行直接表达。所以对于研究随时间变化不同游戏种类的销量的变化情况，借助 position + angle 达到了非常好的描述效果。

但是准确度并不是设计可视化的唯一参考，有时会需要在准确度与其他因素之间进行权衡，尤其是对大量数据进行可视化时，所关心的重点更侧重与整体分布规律、异常等，而不是数值的准确程度 (如热力图)。

目前的一些数据探索分析系统中的自动 encoding 算法都参考了这一思想：

2.2 区分度 (Discriminability)

对于类别类型的变量，可视化设计要保证视觉通道对类别的区分度。比如颜色通道，其在类别数量过多时的区分度会非常差，一般建议对于颜色通道，映射的类别数量不超过 5-7 个。

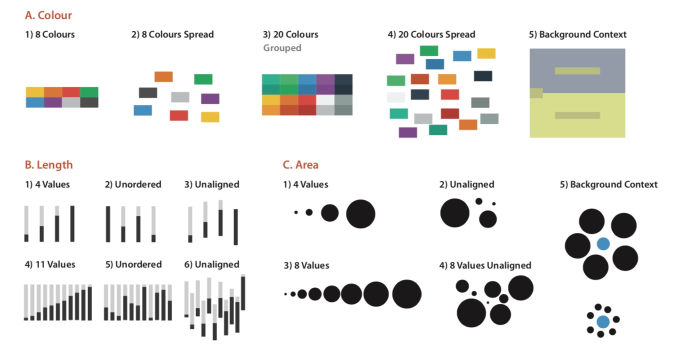
图 2-7 区分度的影响因素 (Maguire, 2014)

如图所示，这些视觉通道在集中按顺序排布在一起的时候区分度尚可，但一旦分散开来，就很难比较两个离得较远的类别是否是一个类别。

区分度主要受以下几个因素的影响：

• 通道本身的性质 (如 color 可以区分的数量大于 shape)

• 空间排布 (如图 2-7 所示)

• 大小 (如图 2-8 所示)

• 类别的数量 (如图 2-7 所示，数量较少时即便随机分布区分布也比较高)
  

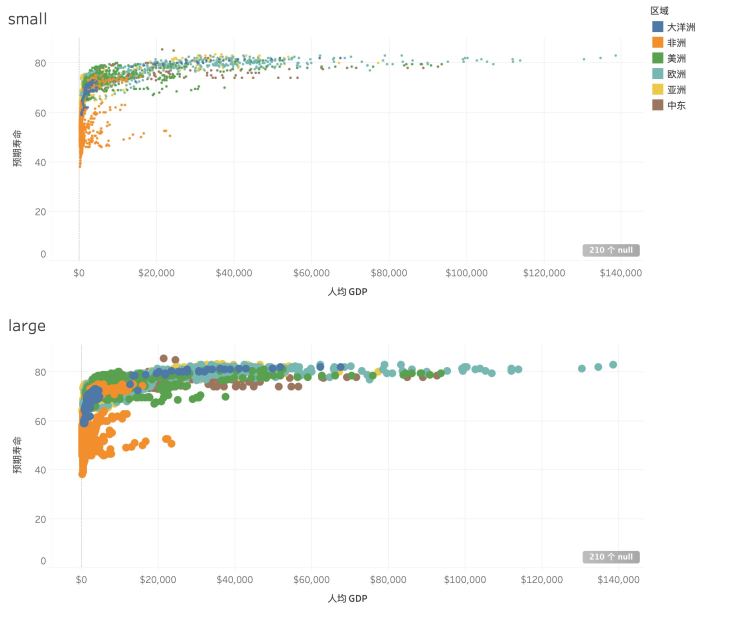
图 2-8 元素大小对区分度的影响

实践案例

提升区分度的方法主要有三种：

（数据集: world indicators）

2.3 显著性 (Salience/Pop-out)

Salience 是指突出 / 强调某些值的能力。研究 salience 时要先了解另一个概念 pre-attentive processing。pre-attentive 是指人类的视觉对于某些特征的捕获会非常快速，对于这类特征，人眼可以在小于 200 到 250 毫秒内快速捕获 (这个时间是人眼快速运动的时间间隔)。人眼在处理这类特征时会使用低级的并行视觉系统 (全局观测)，这是指人眼无需仔细观察一个具体的位置就可以获取到这类信息。

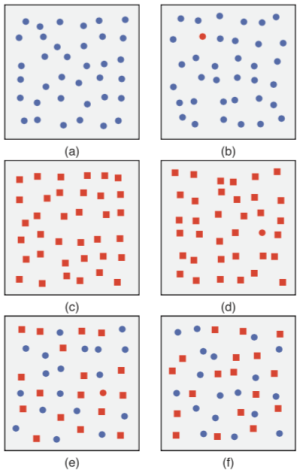
图 2-9 pre-attentive processing (from http://www.datajourneyman.com/2016/03/21/preattentive-processing.html)

如图 2-9 所示，在 (a) (b) 中人眼可以从蓝色的点钟快速捕获到红色的点。在 (c) 和(d)中，虽然没有捕获不同的颜色那么迅速，但也可以捕获到形状不同的点（圆形和方形）

但是，有时两个 pre-attentive 特征组合在一起时，会变成非 pre-attentive 的情况，如 (e) 和(f)中，寻找一个红色的圆形就会变得困难很多，这种情况被称为 conjunction。

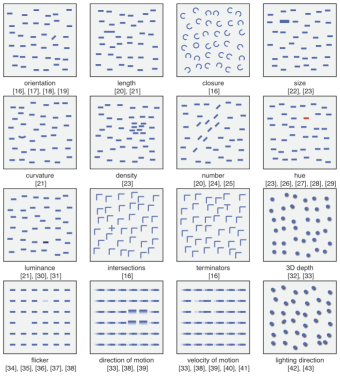
图 2-10 一些 pre-attentive (from http://www.datajourneyman.com/2016/03/21/preattentive-processing.html)

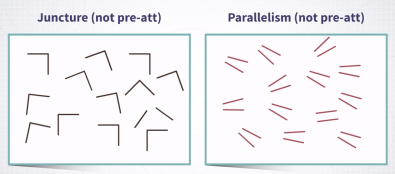
图 2-11 非 pre-attentive 的例子

对于非 pre-attentive 的情况，人眼需要扫描整个图片，去核对每一个细节。这时人眼处理的方式则有并行化的转为序列化的分析方式。

图 2-12 所示的是 MIT 的一个研究小组的捕获的人眼在分析非 pre-attentive 的情况时的焦点移动轨迹

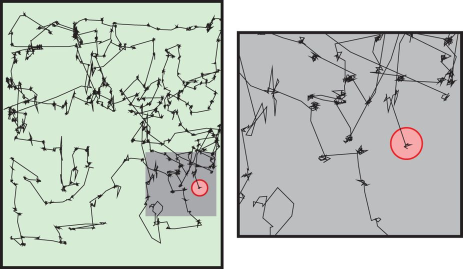
图 2-12 人眼观测非 pre-attentive 时的运动轨迹 (from https://www.nature.com/articles/srep00920/figures/2)

需要注意的时，有些视觉通道的显著性要强于其他通道，如图 2-13 所示，将注意力集中在蓝色圆形上要比将注意力集中在大圆上要容易的多 (此时颜色通道会分散人眼对大小通道的注意力)

图 2-13 分别尝试将注意力放在蓝色圆形上和大的圆形上 (from https://www.coursera.org/learn/information-visualization-applied-perception/lecture/9XtS3/salience-pop-out)

需要注意的是，有些通道的显著性并不一定是对称的，如从大圆中找小圆的情况要比从小圆中找大圆的情况要难一些。

实践案例

将需要重点突出的类别使用颜色高亮，其他类别使用灰色。

2.4 可分性 (Separability)

可分性 (Separability) 是指不同通道之间的干涉或独立程度。

如下图所示，尝试找出宽度相同或高度相同的矩形 (左)；尝试找出所有的黄色图形(右) 会相对简单，但尝试找出所有的三角形则会比较困难，这是由于颜色通道对形状通道造成了干扰所致的。

但是这种干涉并不一定是坏事，有时可以利用这种干涉来更有效的表达信息。

图 2-14 展示的是 400 位荷兰老年人的身高体重数据，左侧身高映射到图形的高度而体重映射到图形的宽度。右侧体重映射到颜色而身高不做映射，高度为常数 (Ware, 2012)

2.5 分组与模式构造 (Grouping and Pattern Formation)

分组是用来协助更好的呈现信息的规律与模式，而发现模式与规律又是可视化的重要特性。

关于分组主要是依据 Gestalt 分组规则 (Gestalt Laws of Grouping)，其定义了一些基本的原则， 其中主要包括了邻近度(proximity)，相似度(Similarity)，连接(Connection)，包裹(Enclosure)、闭包(Closure) 以及连续性(Continuity)。

邻近度 (Proximity)

邻近度主要是指人的视觉会倾向于将临近的物体划分为一组。如图 2-15 所示，左侧的图点与点之间的横向距离较短，而右侧的图点与点之间的纵向距离较短，这也带来了视觉感知时对点分组策略的差异。

图 2-15 (from https://www.coursera.org/learn/information-visualization-applied-perception/lecture/fNUHU/grouping-similarity-and-proximity)

图 2-15 左侧人的视觉会人为倾向于将点按照行分组，而右侧人的视觉则倾向于按照列分组。

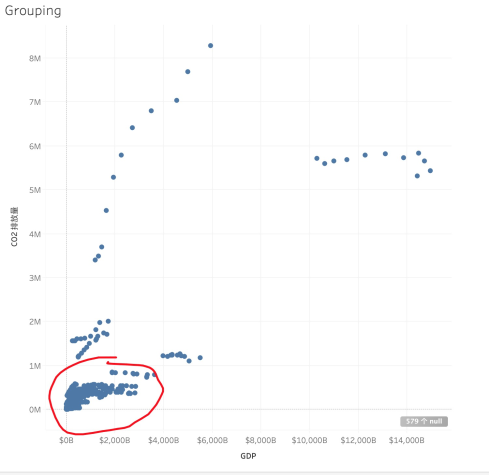
图 2-16 (数据集: World Indicators)

在借助可视化进行数据分析时，如散点图的情况 (图 2-16)，人们会倾向于按照距离将点进行聚类，然后研究每一类的特性与其他类的区别。

相似度 (Similarity)

相似度是指人的视觉会倾向于根据图形的一些特性 (如颜色、形状)，对图形进行分组，如图 2-17 所示。

图 2-17

在图 2-18 中，即使黄色 (亚洲) 的点距离上彼此相聚较远，人眼还是能够快速将其分为一组。

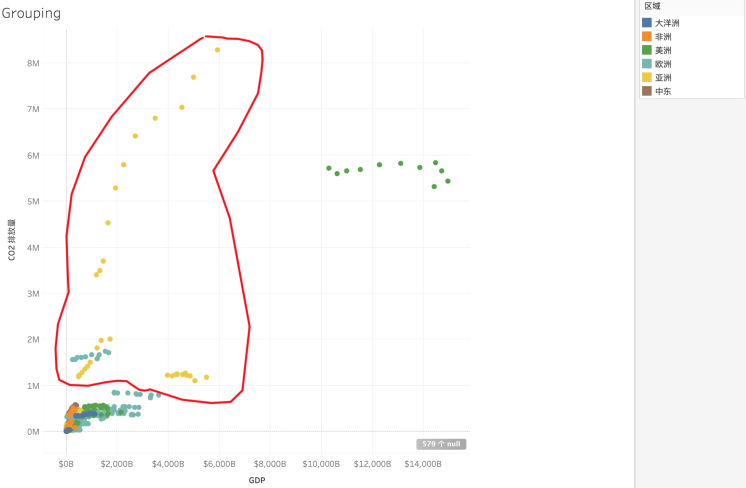
图 2-18 (数据集: World Indicators)

连接 (Connection)

人的视觉会倾向于将被连接在一起的图形视为一组，如下图 2-19 所示，即使图形的颜色不同，通过连接，人眼也会将其视为一组。

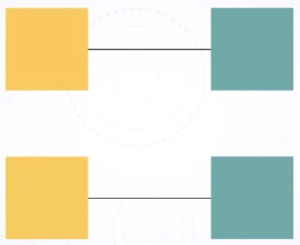
图 2-19 (from https://www.coursera.org/learn/information-visualization-applied-perception/lecture/rvBdz/grouping-connection-and-enclosure)

包裹 (Enclosure)

指人们倾向于将被包裹的物体视为一组，如图 2-20 所示，即是物体已经通过连线连接，但人的视觉仍会优先将被红线包裹的物体视为一组。

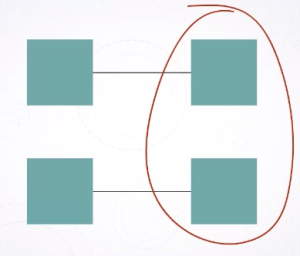
图 2-20 (from https://www.coursera.org/learn/information-visualization-applied-perception/lecture/rvBdz/grouping-connection-and-enclosure)

在可视化应用中，一个经典的用法便是 Bubble sets， 如图 2-21 所示

图 2-21 Bubble sets (from http://vialab.science.uoit.ca/portfolio/bubblesets)

分组方式的层级

通过上面的案例可以看出，不同的分组技巧在人的视觉看来是有着不同的层级 / 优先级的：Enclosure > Connection > Similarity > Proximity。此外还有两个非常神奇的原则：closure 和 continuity

闭包 (Closure)

如下图所示，闭包原则 (principle of closure) 是指即便图形本身是不完整的或者被遮挡的，人的会倾向于在脑中补全缺失的部分。

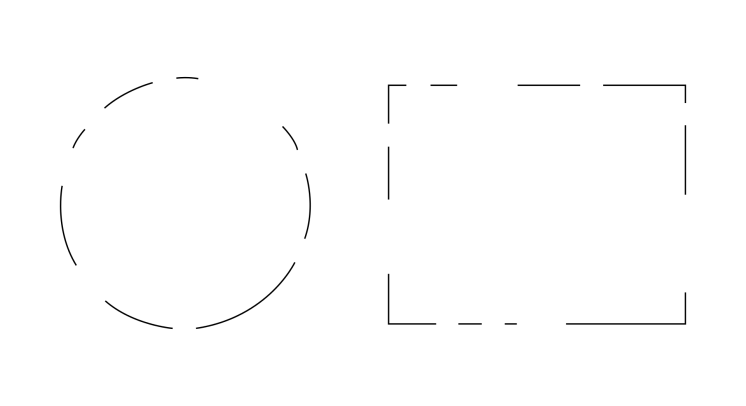
图 2-22 闭包 (from https://en.wikipedia.org/wiki/Principles_of_grouping)

连续性 (Continuity)

连续性原则 (principle of continuity) 是指人的视觉倾向于将连续性被打断的物体重建为一个完整而连续的物体，如图 2-23 所示。

图 2-23 (from https://en.wikipedia.org/wiki/Principles_of_grouping)

总结

不同可视化通道的表达能力相差非常多，除了每个通道可以表达的变量类型不同外，对于同一种类型的变量，不同的通道的表达准确性也不同，而可表达性与表达准确性是设计可视化 encoding 算法重要参考。除此之外，可视化设计还要结合可视化本身的目的，调整映射的规则，而不是一味的使用准确度作为唯一的评分标准。可视化通道的一些特性还有优先级与干涉性的概念，当一个可视化中出现多个通道时，要考虑通道的优先级是否与可视化想表达的内容相符 (更重要的变量要使用更重要的通道)；同时，由于存在干涉，有些通道要避免同时出现并映射不同的变量。

参考资料

Infomation Visualization: Applied Perception 课程链接：https://www.coursera.org/learn/information-visualization-applied-perception/home/welcome

• Cleveland, W., & McGill, R. (1984). Graphical Perception: Theory, Experimentation, and Application to the Development of Graphical Methods. Journal of the American Statistical Association,__79(387), 531-554. doi:10.2307/2288400
• Fechner, G. T., Howes, D. H., & Boring, E. G. (1966). Elements of psychophysics (Vol. 1). New York: Holt, Rinehart and Winston.
• Heer, J., & Bostock, M. (2010, April). Crowdsourcing graphical perception: using mechanical turk to assess visualization design. In Proceedings of the SIGCHI conference on human factors in computing systems (pp. 203-212). ACM.
• Maguire, E. J. (2014). Systematising glyph design for visualization (PhD thesis). Oxford University, UK.
• Mackinlay, J. (1986). Automating the design of graphical presentations of relational information. Acm Transactions On Graphics (Tog), 5(2), 110-141.
• Stevens, S. (1970). Neural Events and the Psychophysical Law. Science,__170(3962), 1043-1050. Retrieved from http://www.jstor.org/stable/1730803
• Stevens, S. S. (1946). On the theory of scales of measurement.
• Ware, Colin. Information visualization: perception for design. Elsevier, 2012.
• Wongsuphasawat, K., Moritz, D., Anand, A., Mackinlay, J., Howe, B., & Heer, J. (2015). Voyager: Exploratory analysis via faceted browsing of visualization recommendations. IEEE transactions on visualization and computer graphics, 22(1), 649-658.
  https://www.yuque.com/chenhao-sv93h/umv780/vsmubd