查找问题

704-二分查找

image.png

  1.     // 盲写通过
  2.     public int search(int[] nums, int target) {
  3.         int left = 0, right = nums.length - 1;
  4.         while (left <= right) {
  5.             int mid = left + (right - left) / 2;
  6.             if (nums[mid] == target) {
  7.                 return mid;
  8.             } else if (nums[mid] > target) {
  9.                 right = mid - 1;
  10.             } else if (nums[mid] < target) {
  11.                 left = mid + 1;
  12.             }
  13.         }
  14.         return -1;
  15.     }

215-数组中的第 K 个最大元素

image.png
代码：

  1.     public int findKthLargest(int[] nums, int k) {
  2.         int len = nums.length;
  3.         int idx = len - k;
  4.         return quicksort(nums, 0, len - 1, idx);
  5.     }
  7.     public int quicksort(int[] nums, int start, int end, int idx) {
  8.         if (start > end) {
  9.             return -1;
  10.         }
  11.         int pivotIdx = partition(nums, start, end, idx);
  12.         if (pivotIdx == idx) {
  13.             return nums[pivotIdx];
  14.         } else if (pivotIdx < idx) { // 基准pivotIdx小于idx时，说明预期结果在idx右侧，则对右侧进行递归遍历
  15.             return quicksort(nums, pivotIdx + 1, end, idx);
  16.         } else {
  17.             return quicksort(nums, start, pivotIdx - 1, idx);
  18.         }
  19.     }
  21.     public int partition(int[] nums, int start, int end, int idx) {
  22.         int pviot = nums[start];
  23.         int left = start, right = end;
  24.         // 左右开始扫描，将基准值pviot移动到合适的位置
  25.         while (left != right) {
  26.             while (left < right && nums[right] >= pviot) {
  27.                 right--;
  28.             }
  29.             while (left < right && nums[left] <= pviot) {
  30.                 left++;
  31.             }
  32.             // 交换 left 和 right 的值
  33.             if (left < right) {
  34.                 int tmp = nums[left];
  35.                 nums[left] = nums[right];
  36.                 nums[right] = tmp;
  37.             }
  38.         }
  40.         //一次排序结束后，left和right抵达重合点，将基准值移动到这里
  41.         int p = nums[start];
  42.         nums[start] = nums[left];
  43.         nums[left] = p;
  45.         return left;
  46.     }

33-搜索旋转排序数组

image.png
代码：

  1.     public int search1(int[] nums, int target) {
  2.         Map<Integer, Integer> idxMap = new HashMap<>();
  3.         for (int i = 0; i< nums.length; i++) {
  4.             idxMap.put(nums[i], i);
  5.         }
  6.         if (idxMap.containsKey(target)) {
  7.             return idxMap.get(target);
  8.         }
  9.         return -1;
  10.     }
  12.     public int search2(int[] nums, int target) {
  13.         for (int i = 0; i < nums.length; i++) {
  14.             if (nums[i] == target) {
  15.                 return i;
  16.             }
  17.         }
  18.         return -1;
  19.     }
  21.     public int search(int[] nums, int target) {
  22.         if (nums.length == 0) {
  23.             return -1;
  24.         }
  25.         if (nums.length == 1) {
  26.             return nums[0] == target ? 0 : -1;
  27.         }
  28.         int left = 0, right = nums.length -1;
  29.         int mid = 0;
  30.         while (left <= right) {
  31.             mid = (left + right) / 2;
  32.             if (nums[mid] == target) {
  33.                 return mid;
  34.             }
  35.             // 总有一半数据是有序的
  36.             if (nums[left] <= nums[mid]) {
  37.                 //左边数据有序则查找左边数据
  38.                 if (target >= nums[left] && target < nums[mid]){
  39.                     right = mid - 1;
  40.                 } else {
  41.                     left = mid + 1;
  42.                 }
  43.             } else {
  44.                 // 右边数据有序则查找右边数据
  45.                 if (target > nums[mid] && target <= nums[right]) {
  46.                     left = mid + 1;
  47.                 } else {
  48.                     right = mid -1;
  49.                 }
  50.             }
  51.         }
  52.         return -1;
  53.     }

81-搜索旋转排序数组II

image.png
代码：

  2.     public boolean search(int[] nums, int target) {
  3.         if (nums.length == 0) {
  4.             return false;
  5.         }
  6.         if (nums.length == 1) {
  7.             return nums[0] == target ? true : false;
  8.         }
  9.         int left = 0, right = nums.length -1;
  10.         int mid = 0;
  11.         while (left <= right) {
  12.             mid = (left + right) / 2;
  13.             if (nums[mid] == target) {
  14.                 return true;
  15.             }
  16.             // 如果数组中元素有重复的，那旋转后可能无法判断哪一半有序
  17.             if (nums[left] == nums[mid] ){
  18.                 left++;
  19.             } else if (nums[mid] == nums[right]) {
  20.                 right--;
  21.             } else{
  22.                 if (nums[left] <= nums[mid]) {
  23.                     //左边数据有序则查找左边数据
  24.                     if (target >= nums[left] && target < nums[mid]){
  25.                         right = mid - 1;
  26.                     } else {
  27.                         left = mid + 1;
  28.                     }
  29.                 } else {
  30.                     // 右边数据有序则查找右边数据
  31.                     if (target > nums[mid] && target <= nums[right]) {
  32.                         left = mid + 1;
  33.                     } else {
  34.                         right = mid -1;
  35.                     }
  36.                 }
  37.             }
  38.         }
  39.         return false;
  40.     }

34-排序数组查元素第一个/最后一个idx（二分）

image.png
代码：

  1.     public int[] searchRange(int[] nums, int target) {
  2.         if (nums.length == 0) {
  3.             return new int[]{-1, -1};
  4.         }
  5.         int firstPosition = findFirstPosition(nums, target);
  6.         if (firstPosition == -1 ) {
  7.             return new int[]{-1, -1};
  8.         }
  9.         int lastPosition = findLastPosition(nums, target);
  10.         return new int[]{firstPosition, lastPosition};
  11.     }
  13.     /**
  14.      * 找到第一次出现的位置
  15.      * @param nums
  16.      * @param target
  17.      * @return
  18.      */
  19.     public int findFirstPosition(int[] nums, int target) {
  20.         int left = 0, right = nums.length - 1;
  21.         while (left < right) {
  22.             int mid = (left + right) / 2;
  23.             if (nums[mid] < target) {
  24.                 left = mid + 1;
  25.             } if (nums[mid] == target) {
  26.                 right = mid;
  27.             } else if (nums[mid] > target) {
  28.                 right = mid - 1;
  29.             }
  30.         }
  31.         if (nums[left] == target) {
  32.             return left;
  33.         }
  34.         return -1;
  35.     }
  37.     /**
  38.      * 向右查找最后一次出现的位置
  39.      * @param nums
  40.      * @param target
  41.      * @return
  42.      */
  43.     public int findLastPosition(int[] nums, int target) {
  44.         int left = 0, right = nums.length - 1;
  45.         while (left < right) {
  46.             // 比如：left=4,right=5，此时 mid = 4，nums[mid]=target，left=mid 操作一直是 left=4，right=5，进入死循环
  47.             int mid = (left + right + 1) / 2;
  48.             if (nums[mid] < target) {
  49.                 left = mid + 1;
  50.             } if (nums[mid] == target) {
  51.                 left = mid;
  52.             } else if (nums[mid] > target) {
  53.                 right = mid - 1;
  54.             }
  55.         }
  56.         return left;
  57.     }

35-搜索插入位置

image.png
题意分析：

  • 查找和插入两个条件，根据二分查找判断数组中是否存在target元素，存在直接返回，不存在则返回元素插入位置（保证数组整体有序）

解题思路：

  • 二分查找，判断条件记录什么时候更新索引位置。

注意点：

  • 插入时需要记录元素要插入的位置。

扩展：
代码：

  1.     public int searchInsert(int[] nums, int target) {
  2.         return binarySearch(nums, target);
  3.     }
  5.     public int binarySearch(int[] nums, int target) {
  6.         int n = nums.length;
  7.         int left = 0, right = n - 1;
  8.         int ans = n;
  9.         while (left <= right) {
  10.             int mid = left + (right - left) / 2;
  11.             System.out.println("mid = " + mid);
  12.             if (nums[mid] == target) {
  13.                 return mid;
  14.             } else if (nums[mid] > target) {
  15.                 ans = mid;
  16.                 right = mid - 1;
  17.             } else if (nums[mid] < target){
  18.                 left = mid + 1;
  19.             }
  20.         }
  21.         return ans;
  22.     }

去重问题

26-删除有序数组中的重复项

image.png
代码：

  1. public int removeDuplicates(int[] nums) {
  2.         if (nums.length == 0) {
  3.             return nums.length;
  4.         }
  5.         int slow = 1, fast = 1;
  6.         while (fast < nums.length){
  7.             if (nums[fast] == nums[slow-1]) {
  8.                 fast++;
  9.             } else {
  10.                 nums[slow++] = nums[fast++];
  11.             }
  12.         }
  13.         return slow;
  14.     }

80-删除有序数组中的重复项II

image.png
代码：

  1.     public int removeDuplicates(int[] nums) {
  2.         if (nums.length == 0 || nums.length == 1) {
  3.             return nums.length;
  4.         }
  5.         int slow = 2, fast = 2;
  6.         while (fast < nums.length){
  7.             if (nums[fast] == nums[slow-2]) {
  8.                 fast++;
  9.             } else {
  10.                 nums[slow++] = nums[fast++];
  11.             }
  12.         }
  13.         return slow;
  14.     }

710-黑名单中的随机数

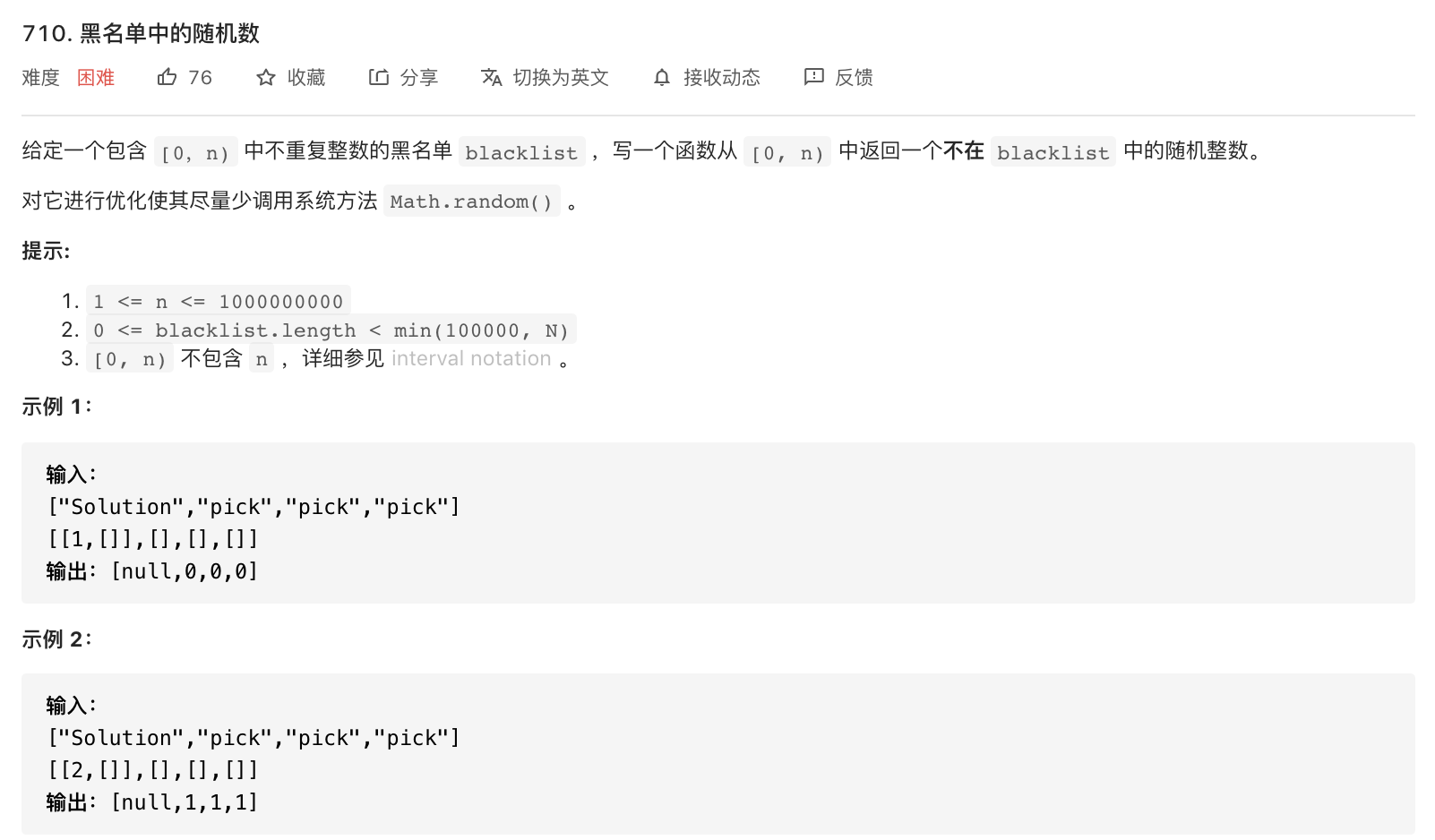
image.png
题意分析：

  • [0, n-1] 中去掉一些数，访问剩下的数。

解题思路：

  1. 直接用集合去重。（存储 [0, n-1] 个元素，内存超出限制）
  2. 黑名单元素重定向。构建 [whitesize, n-1] 长度的数组（和黑名单数组元素相同），然后将黑名单的元素直接映射到这个数组。

注意点：

  • 黑名单中大于 whitesize 索引的元素直接过滤，比较随机数索引不到，只需要对黑名单中小于 whitesize 的元素映射即可。
  • 求解返回时，如果是黑名单中数据重定向，白名单数据直接返回，会用到 Map 的 getOrDefault() 方法。

代码：

  1. public class RandomBlackList_710 {
  2.     Set<Integer> set = new HashSet<>();
  3.     Map<Integer, Integer> map = new HashMap<>();
  4.     int whitesize;
  6.     /**
  7.      * 解题思路：
  8.      *  1、构建白名单set，初始元素和黑名单一致。
  9.      *  2、将黑名单中大于 whitesize 的元素从 set 移除，将小于 whitesize 的元素映射到 set 的剩余元素
  10.      * @param n
  11.      * @param blacklist
  12.      */
  13.     public RandomBlackList_710(int n, int[] blacklist) {
  14.         whitesize = n - blacklist.length;
  15.         for (int i = whitesize; i < n; i++) set.add(i);
  16.         for (int val : blacklist) set.remove(val);
  18.         Iterator<Integer> iter = set.iterator();
  19.         // 将黑名单数据请求到白名单其他数据
  20.         for (int val : blacklist) {
  21.             if (val < whitesize) {
  22.                 map.put(val, iter.next());
  23.             }
  24.         }
  25.     }
  27.     public int pick() {
  28.         int rand = new Random().nextInt(whitesize);
  29.         return map.getOrDefault(rand, rand);
  30.     }
  32.     public static void main(String[] args) {
  33.         int n = 10;
  34.         int[] blacklist = {1,2,4,8};
  35.         RandomBlackList_710 obj = new RandomBlackList_710(n, blacklist);
  36.         System.out.println("size = " + obj.set.toString());
  37.         System.out.println("map key = " + obj.map.keySet().toString() + "; map val = " + obj.map.values().toString());
  38.         for (int i = 0; i < 10; i++)
  39.             System.out.println(obj.pick());
  40.     }
  41. }

岛屿问题

200-岛屿数量

image.png
题意分析：

  • 当前节点可达的节点集合作为一个岛屿，问题可以归结为图的遍历。

解题思路：

  • dfs 遍历。一次 dfs 遍历所有节点解决不了问题，需要对每个可行节点执行 dfs 逻辑，每一次找到一个岛屿。

注意点：
扩展：
代码：

  1. public class IslandsQuestion_200 {
  3.     int[][] direction = {{-1,0},{1,0},{0,-1},{0,1}};
  4.     char[][] visited;
  5.     char[][] grid;
  6.     int m,n;
  7.     int num;
  9.     public int numIslands(char[][] grid) {
  10.         this.grid = grid;
  11.         m = grid.length;
  12.         n = grid[0].length;
  13.         visited = new char[m][n];
  15.         for (int i = 0; i < m; i++) {
  16.             Arrays.fill(visited[i], '0');
  17.         }
  19.         for (int i = 0; i < m; i++) {
  20.             for (int j = 0; j < n; j++) {
  21.                 if (grid[i][j] == '1' && visited[i][j] == '0') {
  22.                     num++;
  23.                     dfs(i, j);
  24.                 }
  25.             }
  26.         }
  27.         return num;
  28.     }
  30.     /**
  31.      * dfs 遍历：将 '1' 周围关联的 '1' 全部设置为 visited
  32.      * @param x
  33.      * @param y
  34.      */
  35.     private void dfs(int x, int y) {
  36.         if (x < 0 || y < 0 || x >= m || y >= n) {
  37.             return;
  38.         }
  39.         // '0' 不访问， visited-1 表示已经访问
  40.         if ( grid[x][y] == '0' || visited[x][y] == '1') {
  41.             return;
  42.         }
  43.         // 每一轮 dfs 遍历，将 '1' 周围节点的 '1' 都设置为 visited
  44.         visited[x][y] = '1';
  45.         // 将 dfs 可达节点都置为 1，表示访问过
  46.         for (int i = 0; i < direction.length; i++) {
  47.             int tx = x + direction[i][0];
  48.             int ty = y + direction[i][1];
  49.             dfs(tx, ty);
  50.         }
  51.     }
  54.     public static void main(String[] args) {
  55.         IslandsQuestion_200 obj = new IslandsQuestion_200();
  56.         char[][] grid = {
  57.                         {'1','1','0','0','0'},
  58.                         {'1','1','0','0','0'},
  59.                         {'0','0','1','0','0'},
  60.                         {'0','0','0','1','1'}
  61.         };
  62.         int res = obj.numIslands(grid);
  63.         System.out.println("res = " + res);
  64.     }
  65. }

1254-统计封闭岛屿的数量

image.png
题意分析：

  • 和题 200 题目类似，无非就是要过滤掉四个边边上的节点。

解题思路：

  • 判断是先判断边边的节点，过滤掉。

注意点：
扩展：
代码：

  1. public class IslandsClosed_1254 {
  3.     int[][] grid;
  4.     int[][] direction = {{0,-1},{0,1},{-1,0},{1,0}};
  5.     int m,n;
  6.     int res;
  8.     public int closedIsland(int[][] grid) {
  10.         this.grid = grid;
  11.         m = grid.length;
  12.         n = grid[0].length;
  14.         // 对四周节点过滤
  15.         for (int i = 0; i < m; i++) {
  16.             dfs(i,0);
  17.             dfs(i, n - 1);
  18.         }
  19.         for (int i = 0; i < n; i++) {
  20.             dfs(0, i);
  21.             dfs(m - 1, i);
  22.         }
  24.         // 对所以 0（陆地）节点遍历，判断是否能形成一个岛屿
  25.         for (int i = 0; i < m; i++) {
  26.             for (int j = 0; j < n; j++) {
  27.                 if (grid[i][j] == 0) {
  28.                     res++;
  29.                     dfs(i,j);
  30.                 }
  31.             }
  32.         }
  33.         return res;
  34.     }
  36.     public void dfs(int x, int y) {
  37.         if (x < 0 || y < 0 || x >= m || y >= n) {
  38.             return;
  39.         }
  40.         if (grid[x][y] == 1) {
  41.             return;
  42.         }
  43.         // 将访问过的 0（陆地） 设置为 1（海水）
  44.         grid[x][y] = 1;
  45.         for (int i = 0; i < direction.length; i++) {
  46.             int tx = x + direction[i][0];
  47.             int ty = y + direction[i][1];
  48.             dfs(tx, ty);
  49.         }
  50.     }
  51. }

未分类

581-最短无序连续子数组

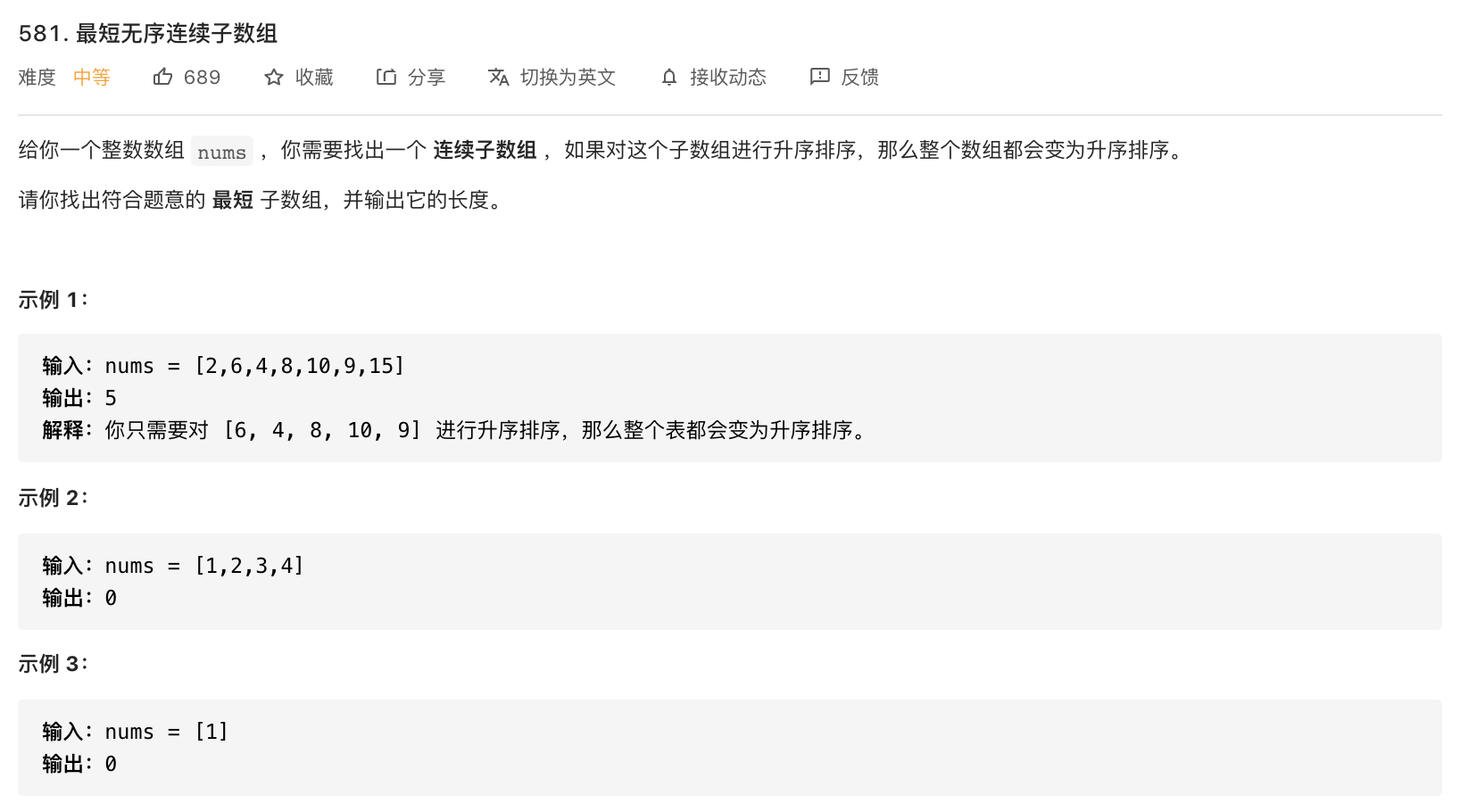
image.png
代码：

  1.     /**
  2.      * 排序 + 遍历（时间复杂度：O(N * logN)
  3.      *
  4.      * 复制一个数组并排序，遍历对比left和right区间
  5.      * @param nums
  6.      * @return
  7.      */
  8.     public int findUnsortedSubarray2(int[] nums) {
  9.       int len = nums.length;
  10.         int[] sorted = Arrays.copyOf(nums, nums.length);
  11.         Arrays.sort(sorted);
  12.         System.out.println("nums   = " + Arrays.toString(nums));
  13.         System.out.println("sorted = " + Arrays.toString(sorted));
  14.         int left = 0, right = len - 1;
  15.         int l = -1, r = -1;
  16.         for (; left < len; left++) {
  17.             if (nums[left] != sorted[left]) {
  18.                 l = left;
  19.                 break;
  20.             }
  21.         }
  22.         for (; right >= 0; right--) {
  23.             if (nums[right] != sorted[right]) {
  24.                 r = right;
  25.                 break;
  26.             }
  27.         }
  28.         System.out.println("l = " + l + ";  r = " + r);
  30.         return l != r ? r - l + 1 : 0;
  31.     }
  33.     /**
  34.      * 双指针
  35.      * @param nums
  36.      * @return
  37.      */
  38.     public int findUnsortedSubarray(int[] nums) {
  39.         int len = nums.length;
  41.         int left = 0, right = 0;
  42.         int max = Integer.MIN_VALUE;
  43.         int min = Integer.MAX_VALUE;
  44.         // 双指针左右扫描，找出 left 和 right
  45.         for (int i = 0; i < len; i++) {
  46.             // 找 right。从左到右遍历，如果某个元素小于前面所有元素的最大值，则无序，更新 right
  47.             if (nums[i] >= max) {
  48.                 max = nums[i];
  49.             } else {
  50.                 right = i;
  51.             }
  53.             // 找left。从右往左遍历，如果某个元素大于前面所有元素的最小值，则无序，更新left
  54.             if (nums[len - i -1] <= min) {
  55.                 min = nums[len - i - 1];
  56.             } else {
  57.                 left = len - i - 1;
  58.             }
  59.         }
  60.         System.out.println("left = " + left + ";  right = " + right);
  62.         return left == right ? 0 : right - left + 1;
  63.     }

896-单调数列

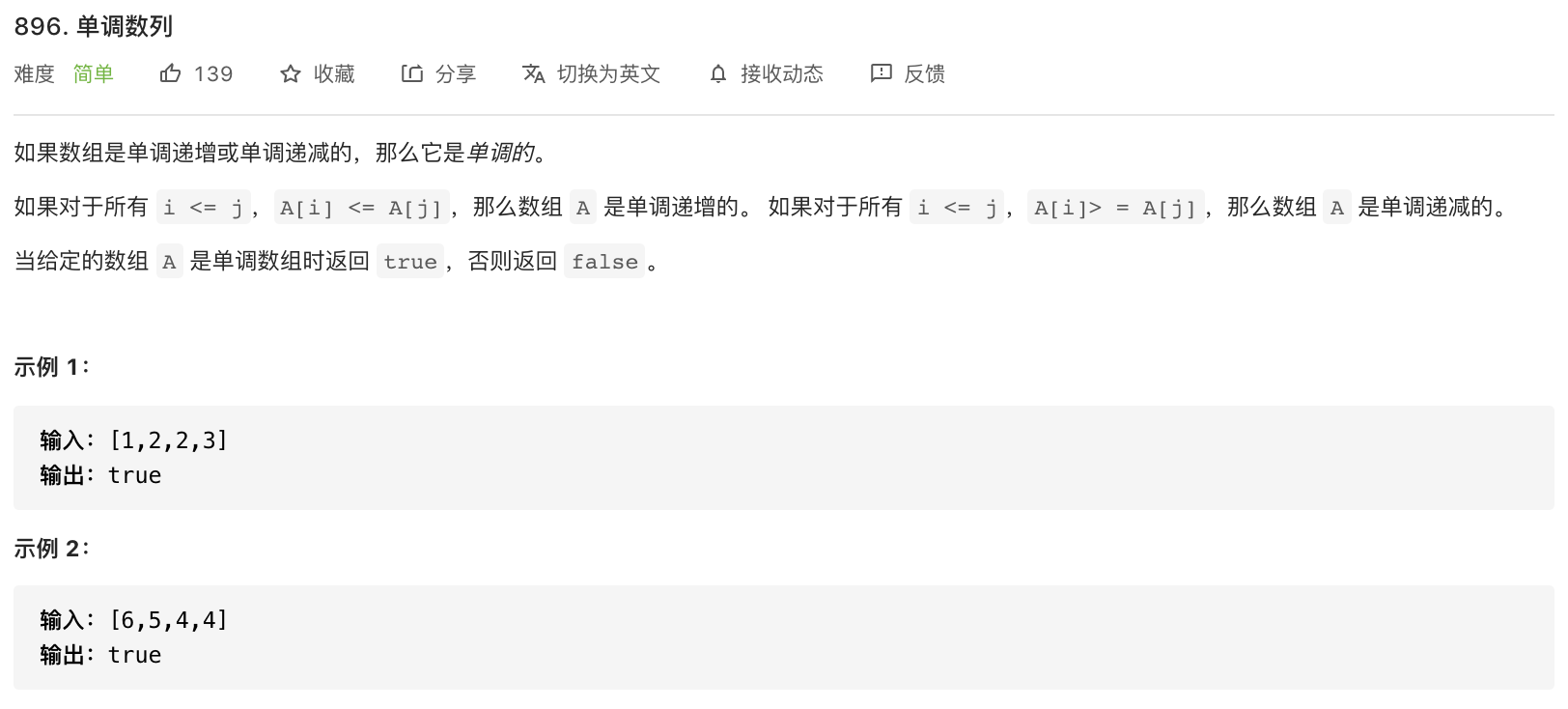
image.png
代码：

  1.     public boolean isMonotonic(int[] nums) {
  2.         int len = nums.length;
  4.         boolean isInc = true, isDec = true;
  5.         // 如果不是单调递增或者单调递减，isInc 和 isDec 都为 false
  6.         for (int i = 0; i < len - 1; i++) {
  7.             // 一对递增数据，isDec = false;
  8.             if (nums[i] < nums[i+1]) {
  9.                 isDec = false;
  10.             }
  12.             if (nums[i] > nums[i+1]) {
  13.                 isInc = false;
  14.             }
  15.         }
  16.         return isInc || isDec;
  17.     }

1337-矩阵中战斗力最弱的 K 行

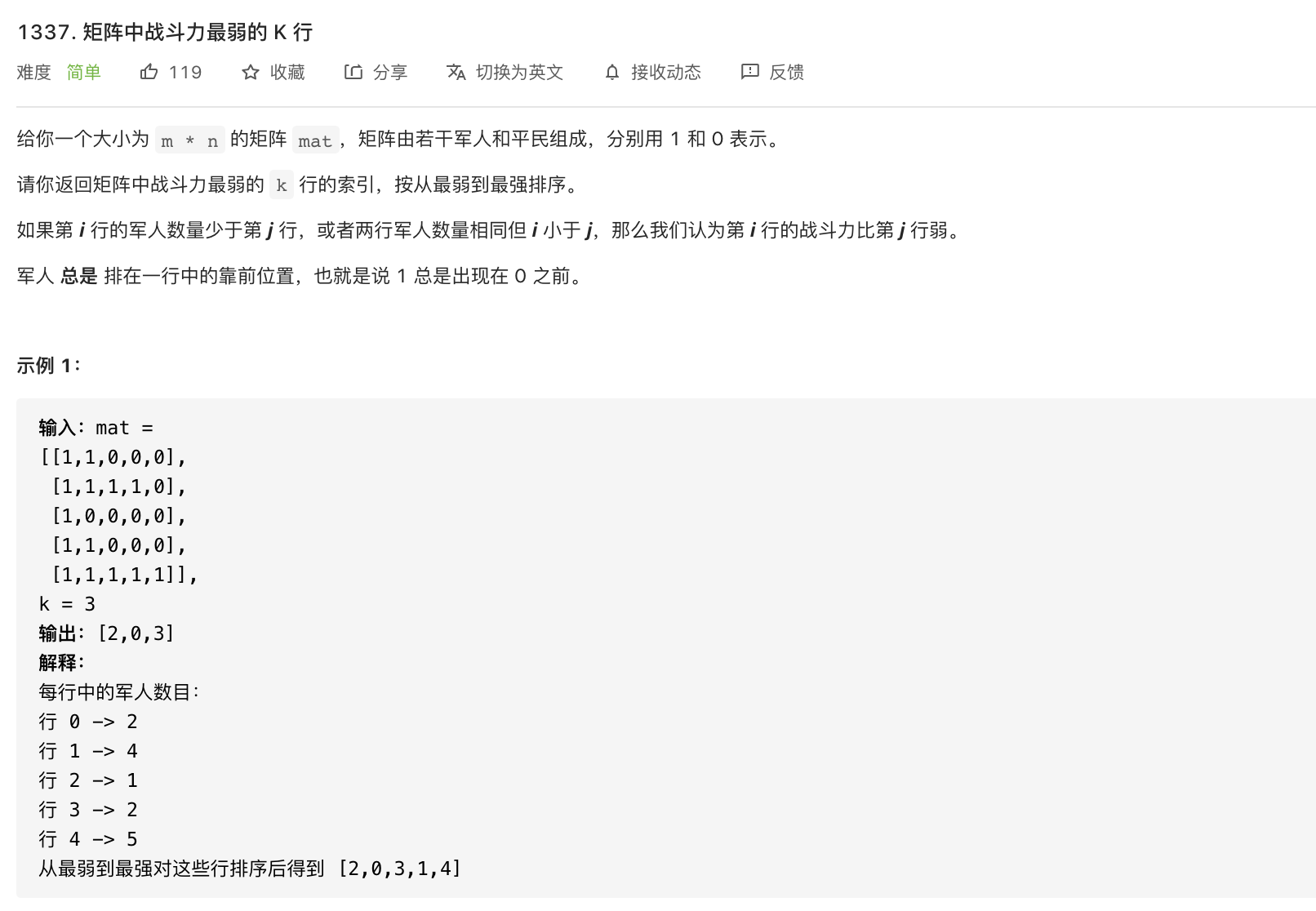
image.png
代码：

  1.     public int[] kWeakestRows(int[][] mat, int k) {
  2.         int m = mat.length, n = mat[0].length;
  4.         for(int i = 0; i < m; i++) {
  5.             for (int j =0; j< n; j++) {
  6.                 System.out.print(mat[i][j] + " ");
  7.             }
  8.             System.out.println();
  9.         }
  11.         // 记录行号和1的个数
  12.         int[][] cntArr = new int[m][2];
  13.         for (int i = 0; i < m; i++) {
  14.             // 对每一行执行二分查找，找出 1 的个数
  15.             int[] arr = mat[i];
  16.             int pos = binarySearch(arr);
  17.             cntArr[i][0] = i;
  18.             cntArr[i][1] = pos + 1;
  19.         }
  21.         for (int i = 0; i < cntArr.length; i++) {
  22.             System.out.println("行:1数量 == " + cntArr[i][0] + ":" + cntArr[i][1]);
  23.         }
  25.         // 自定义比较器排序，先按1的个数升序排序，再按行号升序排序
  26.         Arrays.sort(cntArr, new Comparator<int[]>() {
  27.             @Override
  28.             public int compare(int[] o1, int[] o2) {
  29.                 if (o1[1] != o2[1]) {
  30.                     return (o1[1] - o2[1]);
  31.                 } else {
  32.                     return (o1[0] - o2[0]);
  33.                 }
  34.             }
  35.         });
  37.         System.out.println("-------排序后——--------");
  38.         for (int i = 0; i < cntArr.length; i++) {
  39.             System.out.println("行:1数量 == " + cntArr[i][0] + ":" + cntArr[i][1]);
  40.         }
  42.         // 输出前 k 行行号
  43.         int[] ret = new int[k];
  44.         for(int i = 0; i < k; i++) {
  45.             ret[i] = cntArr[i][0];
  46.             System.out.println(ret[i]);
  47.         }
  48.         return ret;
  49.     }
  51.     /**
  52.      * 二分查找每一行 1 的数量
  53.      * @param arr
  54.      * @return
  55.      */
  56.     public int binarySearch(int[] arr) {
  57.         int left = 0, right = arr.length - 1;
  58.         int pos = -1;
  59.         while (left <= right) {
  60.             int mid = left + (right - left) / 2;
  61.             if (arr[mid] == 0) {
  62.                 right = mid - 1;
  63.             } else {
  64.                 pos = mid;
  65.                 left = mid + 1;
  66.             }
  67.         }
  68.         return pos;
  69.     }

88-合并两个有序数组

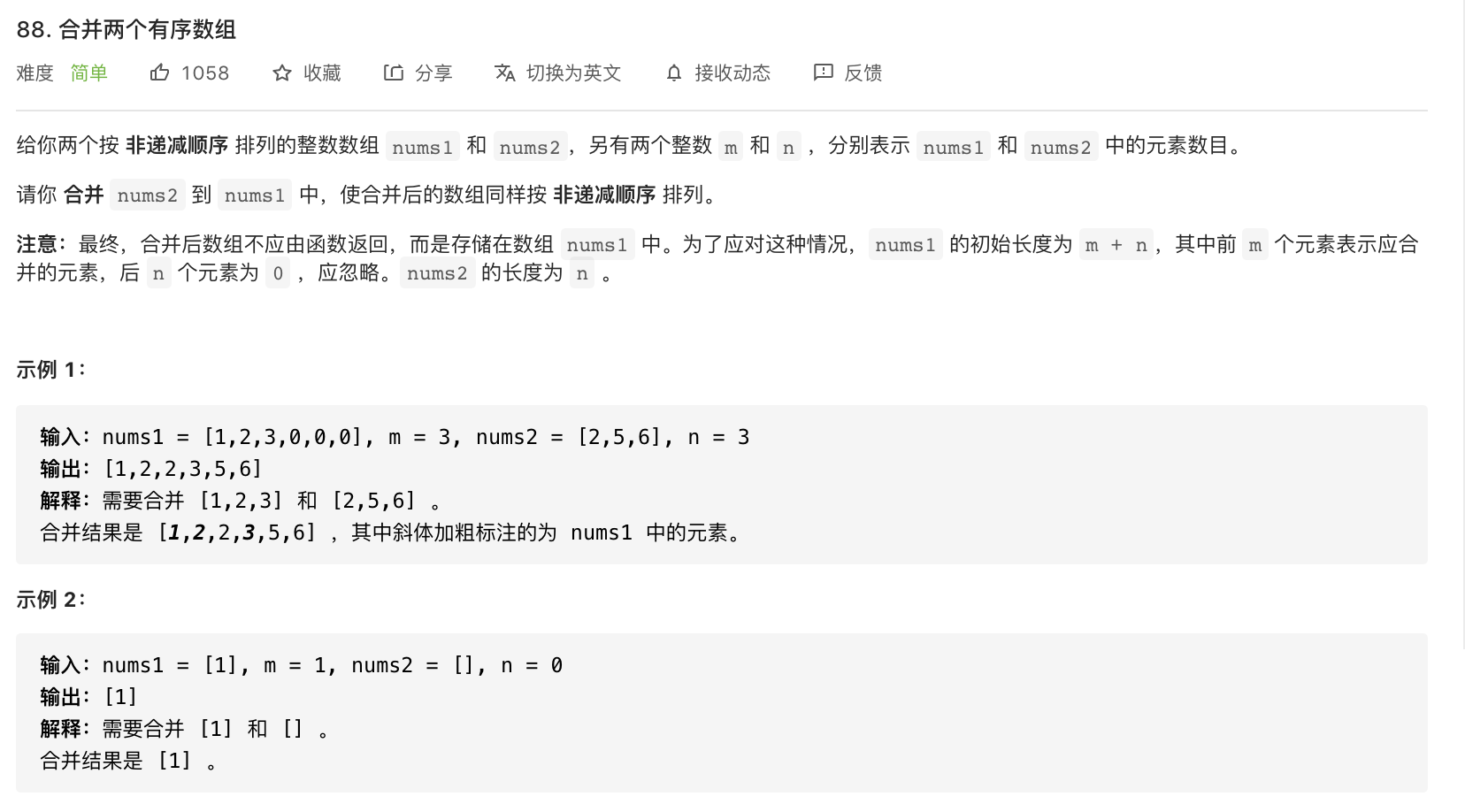
image.png
代码：

  1.     /**
  2.      * 申请长度为 m+n 的额外数组
  3.      * @param nums1
  4.      * @param m
  5.      * @param nums2
  6.      * @param n
  7.      */
  8.     public void merge2(int[] nums1, int m, int[] nums2, int n) {
  9.         int[] tmp = new int[m+n];
  10.         int k = 0;
  11.         int i = 0, j = 0;
  12.         while (i < m && j < n) {
  13.             tmp[k++] = nums1[i] < nums2[j] ? nums1[i++] : nums2[j++];
  14.         }
  16.         while(i < m) {
  17.             tmp[k++] = nums1[i++];
  18.         }
  20.         while (j < n) {
  21.             tmp[k++] = nums2[j++];
  22.         }
  23.         for(int p = 0 ;p < tmp.length; p++) nums1[p] = tmp[p];
  24.         System.out.println("tmp = " + Arrays.toString(nums1));
  25.     }
  27.     /**
  28.      * 原地复制，从尾部空位置开始填充
  29.      * @param nums1
  30.      * @param m
  31.      * @param nums2
  32.      * @param n
  33.      */
  34.     public void merge(int[] nums1, int m, int[] nums2, int n) {
  35.         int i = m - 1;
  36.         int j = n - 1;
  37.         int k = m + n - 1;
  38.         while (i >= 0 && j >= 0) {
  39.             nums1[k--] = nums1[i] > nums2[j] ?  nums1[i--] : nums2[j--];
  40.         }
  41.         System.arraycopy(nums2, 0 , nums1, 0, j + 1);
  42. //        System.out.println("nums = " + Arrays.toString(nums1));
  43.     }

611-有效三角形的个数

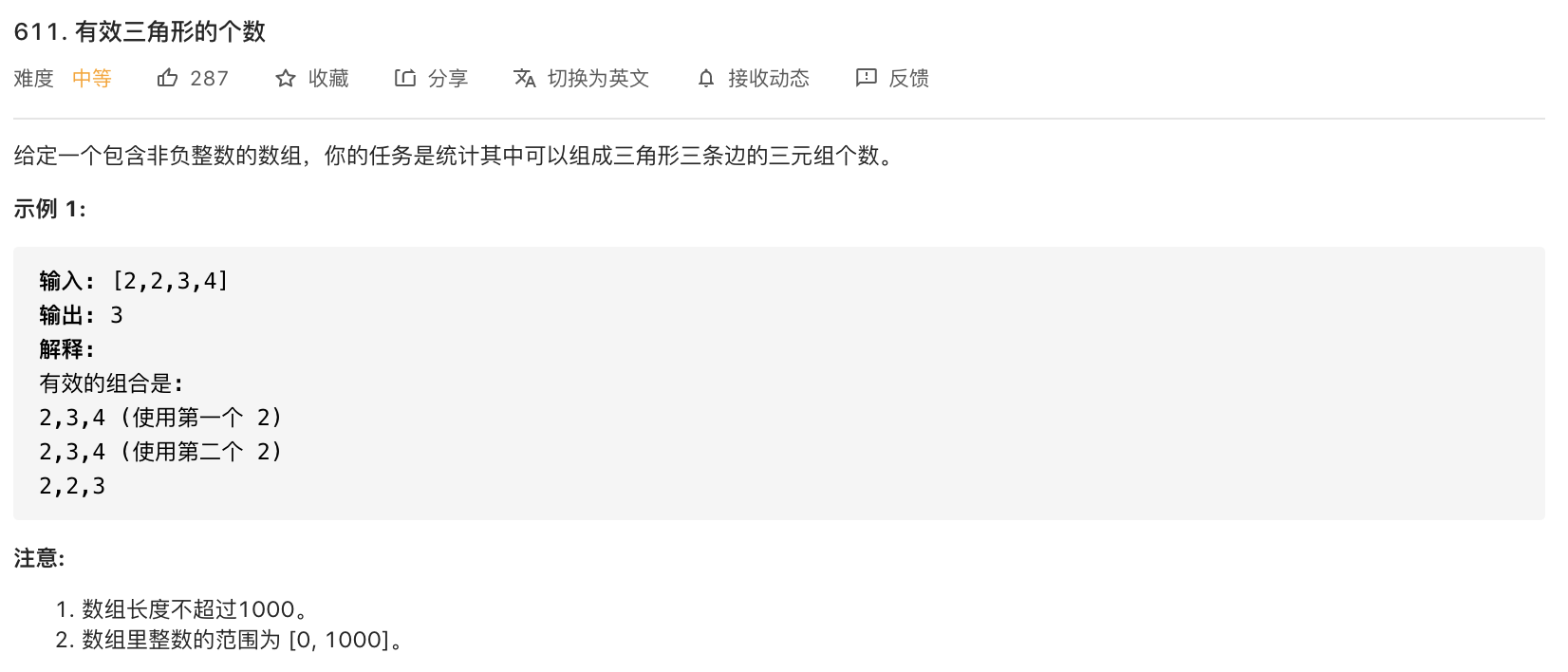
image.png
代码：

  1.     /**
  2.      * 排序 + 二分查找 （时间复杂度 O(N^2 * logN)
  3.      *
  4.      * 注意：System.out 会增加统计时间，造成时间超时
  5.      *
  6.      * @param nums
  7.      * @return
  8.      */
  9.     public int triangleNumber(int[] nums) {
  10.         int len = nums.length;
  11.         if (len <= 2) {
  12.             return 0;
  13.         }
  14.         int ans = 0;
  15.         Arrays.sort(nums);
  16.         for (int i = 0; i < len-1; i++) {
  17.             for (int j = i+1; j < len; j++) {
  18.                 int left = j + 1, right = len - 1;
  19.                 int k = j;
  20.                 while (left <= right) {
  21.                     int mid = left + (right - left) / 2;
  22.                     if (nums[i] + nums[j] > nums[mid]) {
  23. //                        System.out.println(nums[i] + "-" + nums[j] + "-" + nums[mid]);
  24.                         k = mid;
  25.                         left = mid + 1;
  26.                     } else {
  27.                         right = mid - 1;
  28.                     }
  29.                 }
  30.                 ans += k - j;
  31.             }
  32.         }
  33.         return ans;
  34.     }

912-排序数组

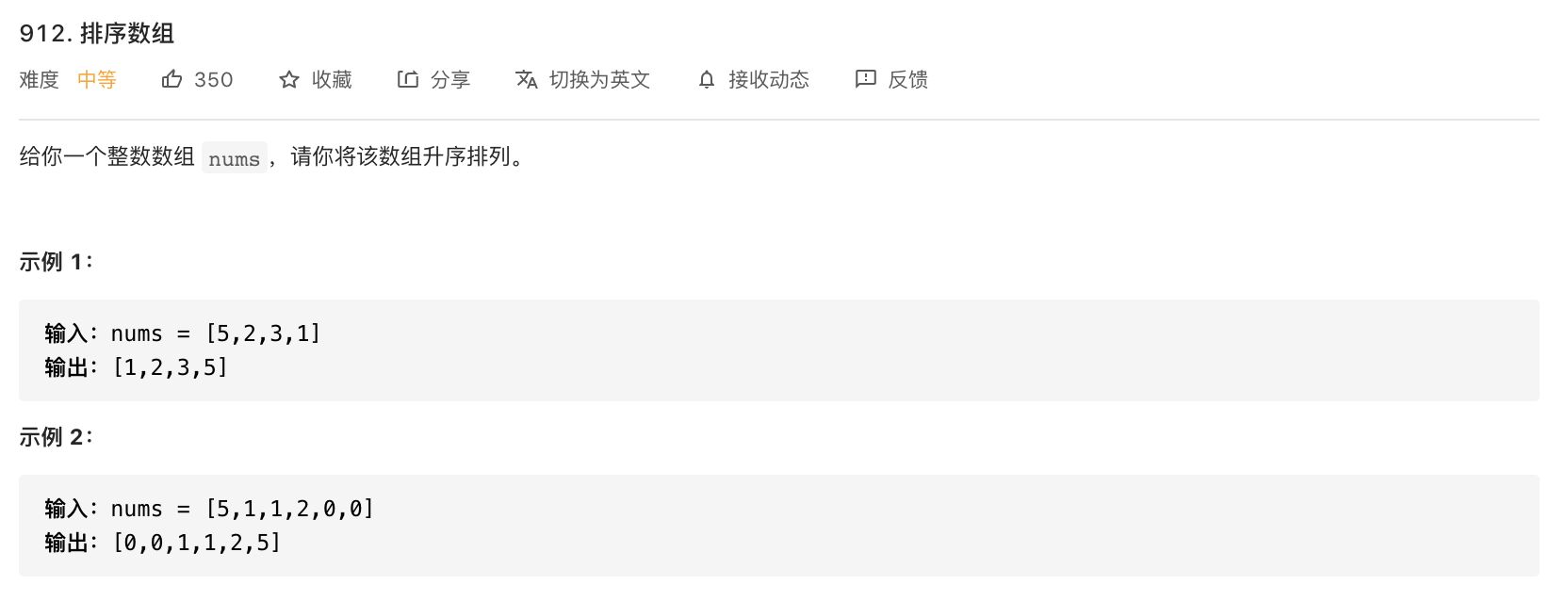
image.png
代码：

  1.     public int[] sortArray(int[] nums) {
  2.         quicksort(nums, 0, nums.length - 1);
  3.         return nums;
  4.     }
  6.     public void quicksort(int[] nums, int startIdx, int endIdx) {
  7.         if (startIdx < endIdx) {
  8.             int pivot = partition(nums, startIdx, endIdx);
  9.             quicksort(nums, startIdx, pivot);
  10.             quicksort(nums, pivot + 1, endIdx);
  11.         }
  12.     }
  14.     /**
  15.      * 一次快排操作
  16.      * @param nums
  17.      * @param startIdx
  18.      * @param endIdx
  19.      * @return
  20.      */
  21.     public int partition(int[] nums, int startIdx, int endIdx) {
  22.         int pivot = startIdx;
  23.         int left = startIdx, right = endIdx;
  24.         while (left != right) {
  25.             while (left < right && nums[right] >= nums[pivot]) right--;
  27.             while (left < right && nums[left] <= nums[pivot]) left++;
  29.             // 交换left 和 right 的值
  30.             if (left < right) {
  31.                 int tmp = nums[left];
  32.                 nums[left] = nums[right];
  33.                 nums[right] = tmp;
  34.             }
  35.         }
  36.         // left/right 重合，交换 pivot 和 left 的值，一次快排完成
  37.         int tmp = nums[pivot];
  38.         nums[pivot] = nums[left];
  39.         nums[left] = tmp;
  41.         return left;
  42.     }

189-旋转数组

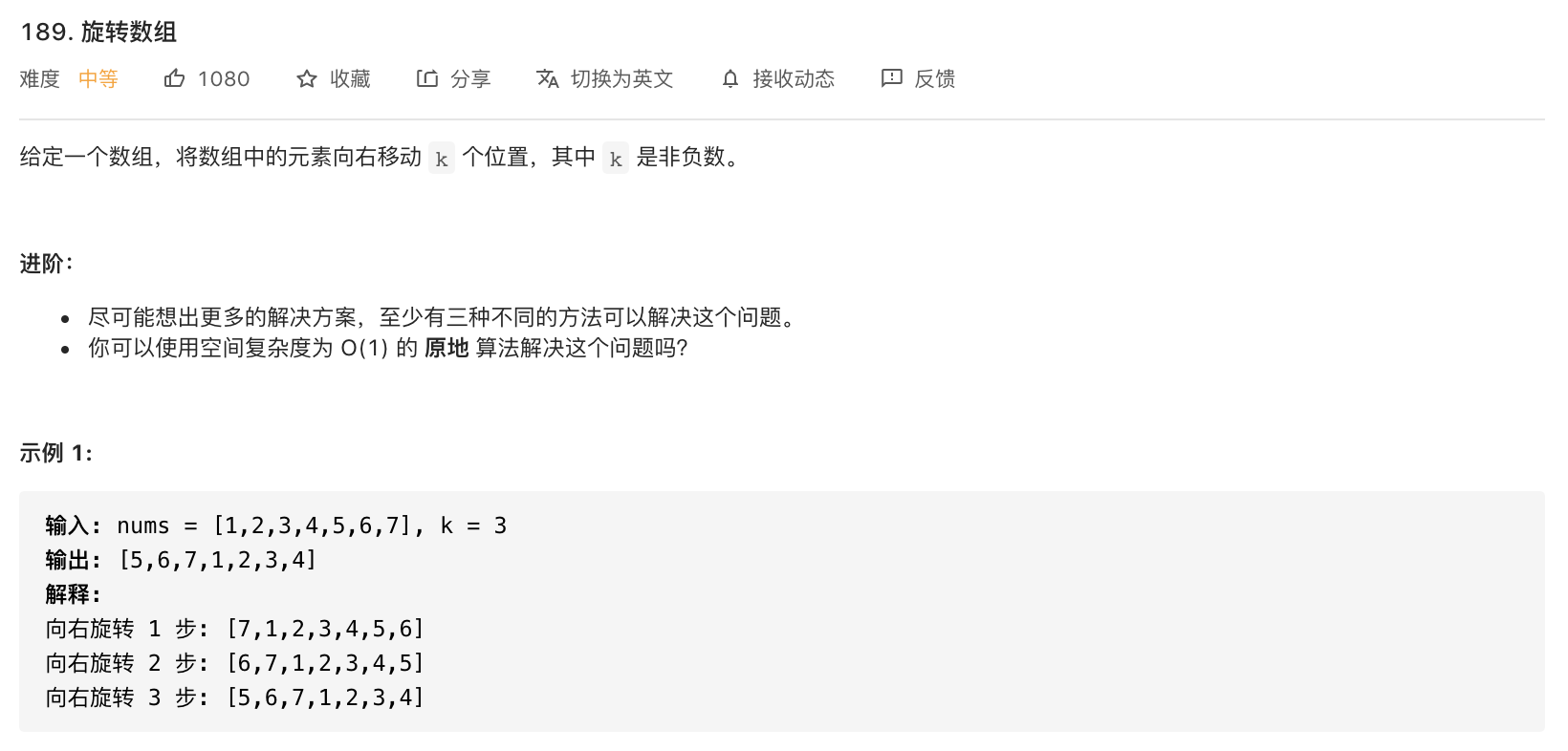
image.png
代码：

  1.     public void rotate(int[] nums, int k) {
  2.         k = k % nums.length;
  3.         reverse(nums, 0, nums.length - 1);
  4.         reverse(nums, 0, k - 1);
  5.         reverse(nums, k, nums.length - 1);
  6.         printArray(nums);
  7.     }
  9.     // 倒序数组
  10.     public void reverse(int[] nums, int start, int end) {
  11.         while (start < end) {
  12.             int tmp = nums[start];
  13.             nums[start] = nums[end];
  14.             nums[end] = tmp;
  15.             start++;
  16.             end--;
  17.         }
  18.     }

915-分隔数组

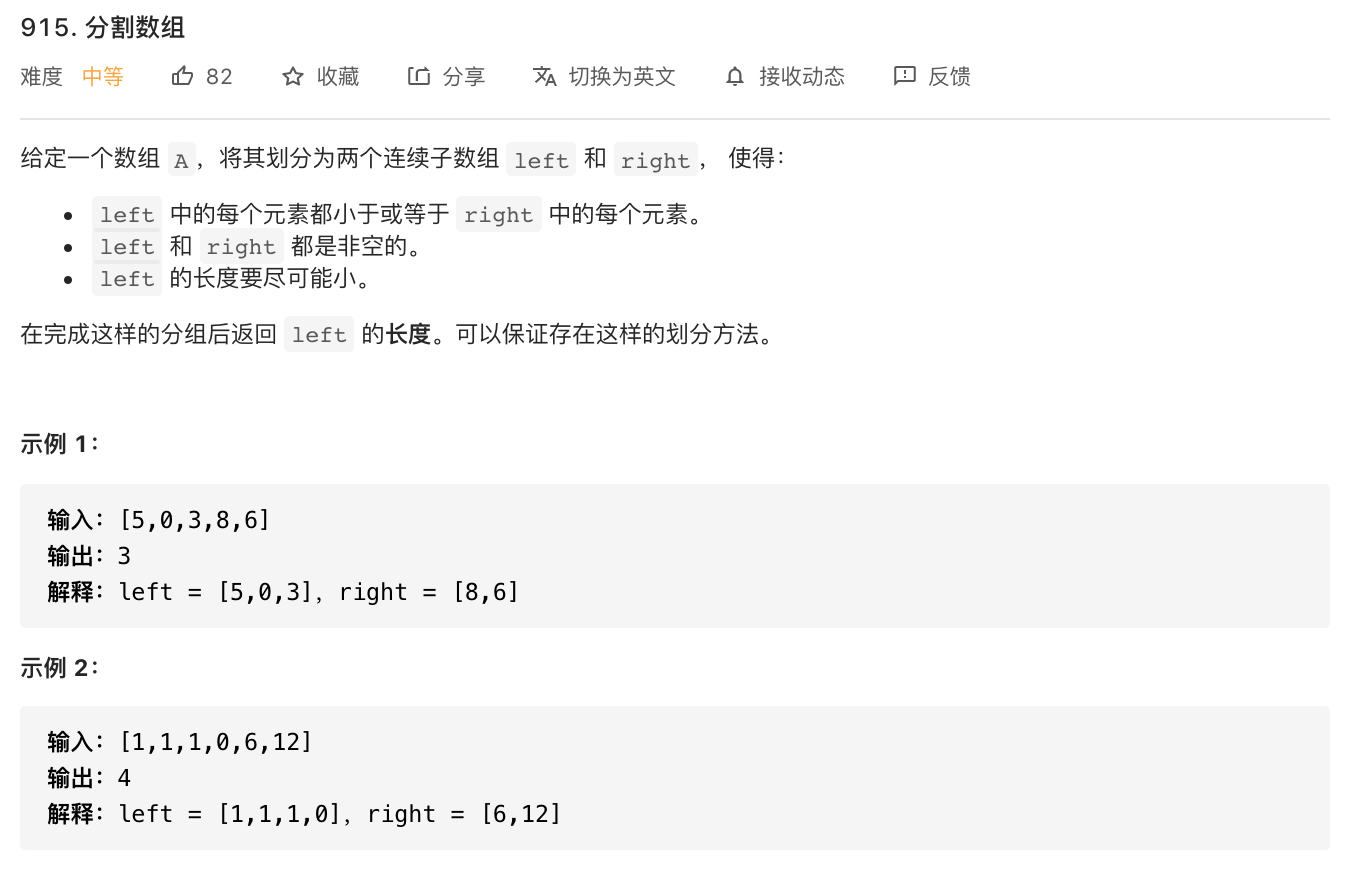
image.png
题意分析：

  • 分隔数组，使得left数组数据都小于right数组数据，且保证left数组长度最小。

解题思路：

  • 多次遍历数组。判断条件 max(left) < min(right)，满足这个条件的最小 idx 值。
    • 时间复杂度：O(n)
    • 空间复杂度：O(n)

注意点：

  • 最后条件判断的时候要考虑 <= 相等的情况。

扩展：

  • 能否减少数组遍历次数。

代码：

  1.     /**
  2.      * 解题思路：
  3.      *  判断条件：max(left) < min(right)，满足这个条件的最小 idx 值。
  4.      *  1、统计 left 数组每个分隔点的最大值
  5.      *  2、统计 right 数组每个分隔点的最小值
  6.      * @param nums
  7.      * @return
  8.      */
  9.     public int partitionDisjoint(int[] nums) {
  10.         int n = nums.length;
  11.         int[] maxleft = new int[n];
  12.         int[] minright = new int[n];
  14.         // left 数组每个位置的最大值
  15.         int max = Integer.MIN_VALUE;
  16.         for (int i = 0; i < n; i++) {
  17.             max = Math.max(max, nums[i]);
  18.             maxleft[i] = max;
  19.         }
  20.         System.out.println("maxleft = " + Arrays.toString(maxleft));
  22.         // right 数组每个位置的最小值
  23.         int min = Integer.MAX_VALUE;
  24.         for (int j = n-1; j >= 0; j--) {
  25.             min = Math.min(min, nums[j]);
  26.             minright[j] = min;
  27.         }
  28.         System.out.println("minright = " + Arrays.toString(minright));
  30.         // 比较切分后 left 和 right 数组的值
  31.         for (int i = 1; i < n; i++) {
  32.             if (maxleft[i-1] <= minright[i]) {
  33.                 return i;
  34.             }
  35.         }
  36.         return n;
  37.     }

27-移除元素

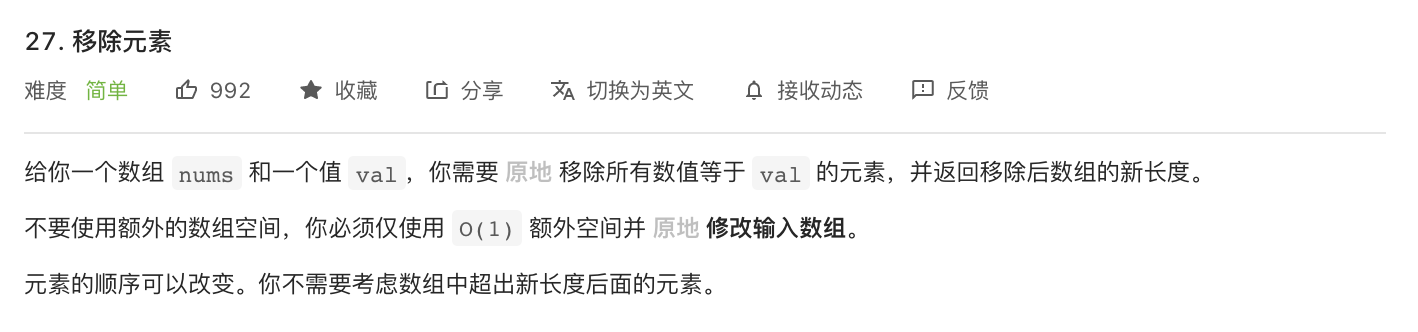
image.png
image.png
题意分析：

  • 原地修改数组，删除数组中值为 val 的元素。

解题思路：

  • 左右指针。左指针维护更新后数组元素，右指针扫描数组。

注意点：

  • 右指针何时扫描。

扩展：
代码：

  1.     /**
  2.      * 解题思路：双指针
  3.      * @param nums
  4.      * @param val
  5.      * @return
  6.      */
  7.     public int removeElement(int[] nums, int val) {
  8.         System.out.println(Arrays.toString(nums));
  9.         int left = 0, right = 0;
  10.         while (right != nums.length) {
  11.             if (nums[right] != val) {
  12.                 nums[left++] = nums[right];
  13.             }
  14.             right++;
  15.         }
  16. //        System.out.println(Arrays.toString(nums));
  17.         return left;
  18.     }

1909-删除一个元素使数组严格递增

image.png
题意分析：

  • 删除一个元素，数组严格递增。

解题思路：

  • 贪心算法。当遇到当前小于前一个数时，则比较当前数和前两个数大小，如果当前数小于前两个数，则删除当前数，如果当前数小于前两个数中的一个（即小于前一个数），则删除前一个数。

注意点：
扩展：
代码：

1-两数之和

image.png
题意分析：

  • 数组中两个元素之和等于 target。

解题思路：

  • 思路一：HashMap 保存 target-nums[i] 元素。
  • 思路二：排序+双指针。

注意点：
扩展：

  • 返回所有和为 target 的元素对，且不存在重复项。

代码：

  1.     /**
  2.      * 思路一：HashMap 保存遍历过的元素和索引
  3.      * @param nums
  4.      * @param target
  5.      * @return
  6.      */
  7.     public int[] twoSum(int[] nums, int target) {
  8.         Map<Integer, Integer> map = new HashMap<>();
  9.         int[] res = new int[2];
  10.         for (int i = 0; i < nums.length; i++) {
  11.             if (map.containsKey(nums[i])) {
  12.                 res[0] = map.get(nums[i]);
  13.                 res[1] = i;
  14.                 return res;
  15.             } else {
  16.                 map.put(target - nums[i], i);
  17.             }
  18.         }
  19.         return res;
  20.     }
  23.     /**
  24.      * 思路二：双指针（求所有两数之和为 sum 的元素对，且不重复）
  25.      * @param nums
  26.      * @param target
  27.      * @return
  28.      */
  29.     public List<List<Integer>> twoSum2(int[] nums, int target) {
  30.         List<List<Integer>> res = new ArrayList<>();
  31.         // 对数组升序排序
  32.         Arrays.sort(nums);
  34.         int low = 0, high = nums.length - 1;
  35.         while (low < high) {
  36.             int low_val = nums[low];
  37.             int high_val = nums[high];
  38.             int sum = low_val + high_val;
  39.             if (sum < target) {
  40.                 low++;
  41.             } else if (sum > target) {
  42.                 high--;
  43.             } else if (sum == target) {
  44.                 List<Integer> list = new ArrayList();
  45.                 list.add(nums[low++]); list.add(nums[high--]);
  46.                 // 如果 low 往右走出现重复元素，则继续右走，high 逻辑也一样
  47.                 while (nums[low] == low_val) low++;
  48.                 while (nums[high] == high_val) high--;
  49.                 res.add(list);
  50.             }
  51.         }
  52.         return res;
  53.     }

15-三数之和

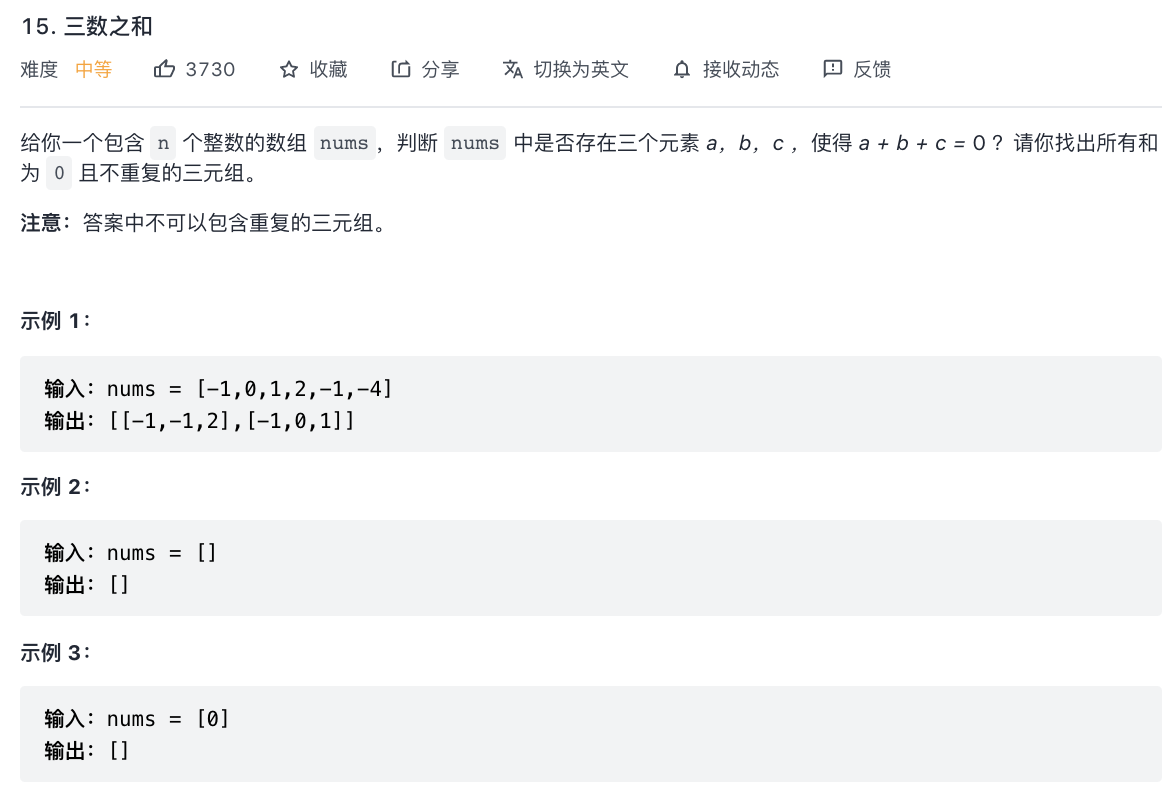
image.png
题意分析：

  • 数组中三个元素和为 target。

解题思路：

  • 排序+双指针。排序数组，遍历数组中每个元素，调用 2Sum 求解，遇到重复遍历元素跳过。

注意点：
扩展：
代码：

  1.     public List<List<Integer>> threeSum(int[] nums) {
  2.         List<List<Integer>> res = new ArrayList<>();
  3.         if (nums.length <= 2) {
  4.             return res;
  5.         }
  6.         Arrays.sort(nums);
  7. //        System.out.println(Arrays.toString(nums));
  8.         for (int i = 0; i < nums.length - 2; i++) {
  9.             List<List<Integer>> twoRes = twoSum(nums,i + 1, 0 - nums[i]);
  10. //            System.out.println("nums[i] = " + nums[i] + "; twoRes = " + twoRes);
  11.             for (int j = 0; j < twoRes.size(); j++) {
  12.                 twoRes.get(j).add(nums[i]);
  13.                 res.add(twoRes.get(j));
  14.             }
  15.             while (i < nums.length -1  && nums[i+1] == nums[i]) i++;
  16.         }
  17.         return res;
  18.     }
  20.     /**
  21.      * 两数只和
  22.      * @param nums
  23.      * @param start
  24.      * @param target
  25.      * @return
  26.      */
  27.     private List<List<Integer>> twoSum(int[] nums, int start, int target) {
  28.         List<List<Integer>> twoRes = new ArrayList<>();
  29.         int low = start, high = nums.length - 1;
  30.         while (low < high) {
  31.             int low_val = nums[low], high_val = nums[high];
  32.             int sum = low_val + high_val;
  33.             if (sum < target) {
  34.                 // 优化
  35.                 while (low < high && nums[low] == low_val) low++;
  36.             } else if (sum > target) {
  37.                 while (low < high && nums[high] == high_val)high--;
  38.             } else if (sum == target) {
  39.                 List<Integer> list = new ArrayList<>();
  40.                 list.add(low_val); list.add(high_val);
  41.                 while (low < high && nums[low] == low_val) low++;
  42.                 while (low < high && nums[high] == high_val) high--;
  43.                 twoRes.add(list);
  44.             }
  45.         }
  46.         return twoRes;
  47.     }

18-四数之和(nSum问题）

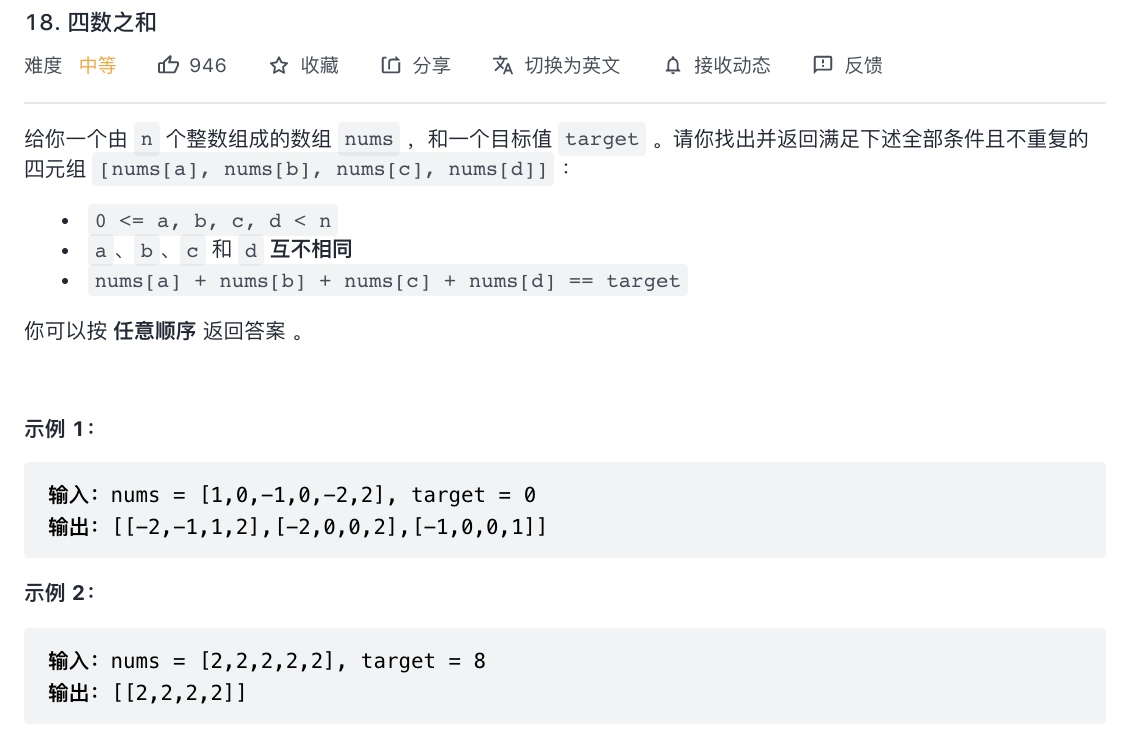
image.png
题意分析：

  • 数组中四个数或者 n 个数和为 target。

解题思路：

  • 思路一：调用 3Sum 求解，没意义。
  • 思路二：通用 nSum 求解，递归调用 (n-1)Sum 求解。

注意点：
扩展：
代码：

  1.     public List<List<Integer>> fourSum(int[] nums, int target) {
  2.         int n = 4;
  3.         Arrays.sort(nums);
  4.         return nSumTarget(nums, n, 0, target);
  5.     }
  7.     /**
  8.      *
  9.      * @param nums
  10.      * @param n   表示几个数之和，比如 n=2，表示两个数之和
  11.      * @param start   数组的开始元素
  12.      * @param target
  13.      * @return
  14.      */
  15.     public List<List<Integer>> nSumTarget(int[] nums, int n, int start, int target) {
  16.         int size = nums.length;
  17.         List<List<Integer>> res = new ArrayList<>();
  18.         // 至少 2Sum，且数组大小不应该小于 n
  19.         if (n < 2 || size < n) return res;
  20.         int low = start, high = nums.length - 1;
  21.         if (n == 2) {
  22.             // 双指针
  23.             while (low < high) {
  24.                 int low_val = nums[low], high_val = nums[high];
  25.                 int sum = low_val + high_val;
  26.                 if (sum < target) {
  27.                     // 优化
  28.                     while (low < high && nums[low] == low_val) low++;
  29.                 } else if (sum > target) {
  30.                     // 优化
  31.                     while (low < high && nums[high] == high_val)high--;
  32.                 } else if (sum == target) {
  33.                     List<Integer> list = new ArrayList<>();
  34.                     list.add(low_val); list.add(high_val);
  35.                     while (low < high && nums[low] == low_val) low++;
  36.                     while (low < high && nums[high] == high_val) high--;
  37.                     res.add(list);
  38.                 }
  39.             }
  40.         } else {
  41.             // n > 2 时，递归计算 (n-1)Sum 结果
  42.             for (int i = start; i < size; i++) {
  43.                 List<List<Integer>> nRes = nSumTarget(nums, n - 1, i + 1, target - nums[i]);
  44.                 for (List<Integer> list : nRes) {
  45.                     list.add(nums[i]);
  46.                     res.add(list);
  47.                 }
  48.                 while (i < size - 1 && nums[i] == nums[i+1]) i++;
  49.             }
  50.         }
  51.         return res;
  52.     }

模版

题意分析：
解题思路：
注意点：
扩展：
代码：