栈和队列
用一个栈实现另一个栈的排序
思路:
- 两个栈的数据转移。辅助栈 help 始终从原始 stack 中拿到最小的元素存入,如果遇到 help 栈中即将压入的数据大于栈顶元素,则需要将 help 栈中的数据全部倒出到 stack 中,压入新的最大元素,重复此过程。
生成窗口最大值的数组
思路:
- 最大堆。申请一个最大堆 pq 维护窗口的元素,且最大元素位于堆顶,不断从 pq 中移除要离开窗口的元素和添加要进入窗口的函数。(Q:但申请辅助结构 pq 的时间复杂度会增加。)
- 双端队列(书中方式,没看懂)。
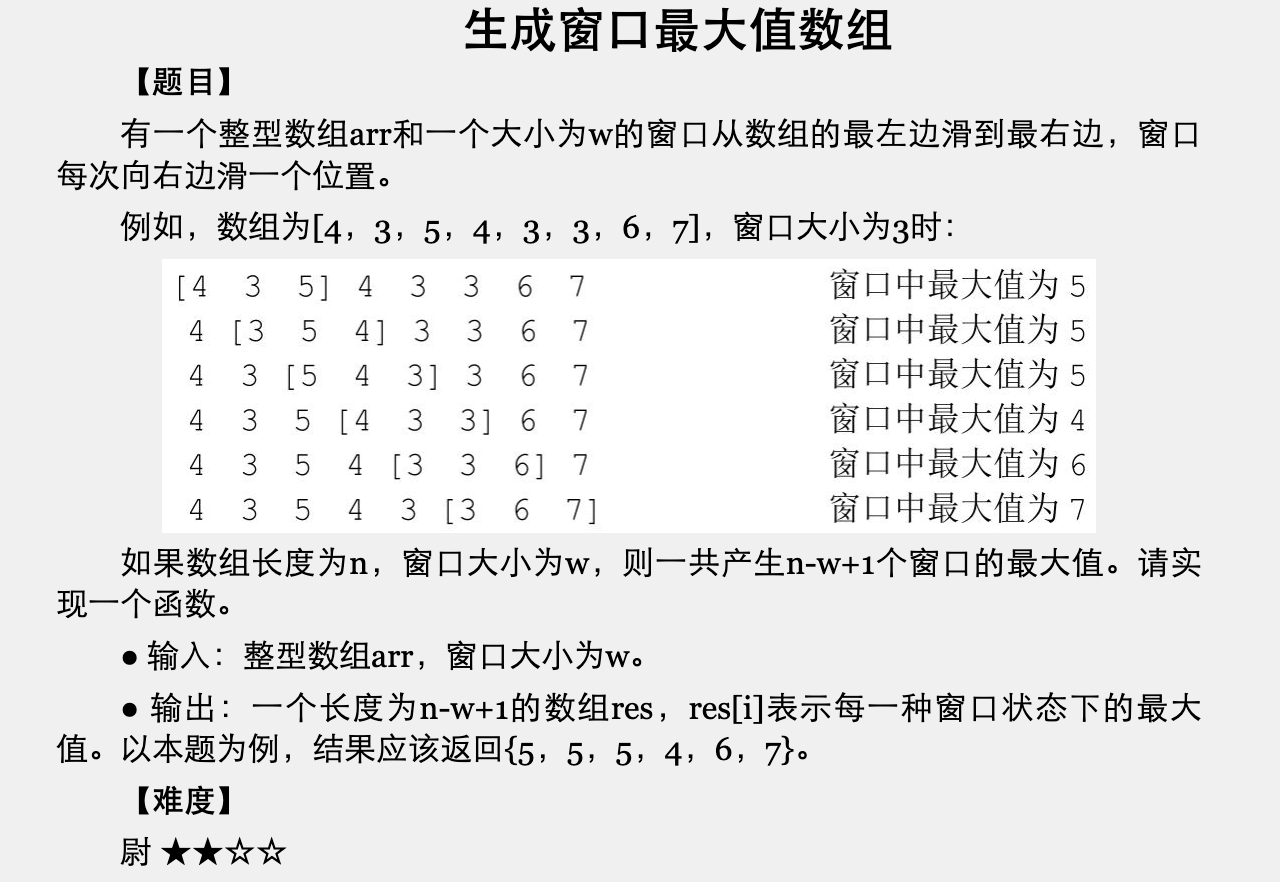
// 最大堆方法public class MaxWindowsArray {public static void main(String[] args) {MaxWindowsArray obj= new MaxWindowsArray();int[] arr = {4,3,5,4,3,3,6,7};int w = 3;// {5,5,5,4,6,7}int[] res = obj.getMaxWindowsArray(arr, w);System.out.println(Arrays.toString(res));}public int[] getMaxWindowsArray(int[] arr, int w) {int[] res = new int[arr.length - w + 1];int idx = 0;// 大堆PriorityQueue<Integer> pq = new PriorityQueue<>(new Comparator<Integer>() {@Overridepublic int compare(Integer o1, Integer o2) {return o2 - o1;}});int left = 0, right = 0;// 生成第一个窗口,并添加到 pq 中while (right < w) {pq.add(arr[right++]);}res[idx++] = pq.peek();int removeWindowVal, enterWindowVal;while (right < arr.length) {// 记录要进窗口和出窗口的元素removeWindowVal = arr[left++];enterWindowVal = arr[right++];// 更新 pq 堆pq.remove(removeWindowVal);pq.add(enterWindowVal);// 取窗口最大值res[idx++] = pq.peek();}return res;}}
单调栈结构
思路:
- 单调递减栈的性质:入栈元素前面比它小的所有元素中离它最近的元素。(当栈的结构被破坏时需要对栈中已有元素进行处理)

https://blog.hackerpie.com/posts/algorithms/monotonous-stacks/monotonous-stacks/
字符串
字符串的统计字符串

package org.apache.java.codeviewguide.string;/*** 给定一个字符串 str,返回 str 的统计字符串。例如,"aaabbadddffc"的统计字符串为"a3b2a1d3f2c1"。** 补充问题:给定一个字符串的统计字符串cstr,再给定一个整数index,返回cstr所代表的原始字符串上的第index个字符。* 例如,"a 1 b 100"所代表的原始字符串上第0个字符是'a',第50个字符是'b'。*/public class CountStringAndFind {public static void main(String[] args) {CountStringAndFind obj = new CountStringAndFind();String str = "aaabbadddffc";String ret = obj.getCountString(str);System.out.println(str + " 压缩后的结果为:" + ret);int idx = 5;char ch = obj.getCharAtIdx(ret, idx);System.out.println(ret + " 压缩串中第 " + idx + " 位置的字符为:" + ch);}/*** 压缩串* @param str* @return** 时间复杂度:O(N)* 空间复杂度:O(1)*/public String getCountString(String str) {char[] chs = str.toCharArray();int len = chs.length;int read = 0, write = 0;int start = 0; // 字符第一次出现的位置for (read = 0; read < len; read++) {if (read == len - 1 || chs[read] != chs[read+1]) {chs[write++] = chs[read];int nums = read - start + 1;// 处理nums计数StringBuilder sb = new StringBuilder();while (nums > 0) {sb.append(nums % 10);nums /= 10;}for (int i = sb.length() - 1; i >= 0; i--) {chs[write++] = sb.charAt(i);}// 更新字符第一次出现的位置start = read + 1;}}StringBuilder ret = new StringBuilder();for (int i = 0; i < write; i++) {ret.append(chs[i]);}return ret.toString();}/*** 从压缩串中找个第k个位置的字符* @param str* @return** 时间复杂度:O(N)* 空间复杂度:O(1)*/public char getCharAtIdx(String str, int idx) {char[] chs = str.toCharArray();char curChar = '_'; // 记录当前遍历的charint sum = 0; // 记录当前字符总数int num = 0; // 记录某个字符总数,比如,a 的 num=102for (int i = 0; i < chs.length; i++) {// Character.isLetterOrDigit(ch) 判断一个字符是字母或数字if (Character.isDigit(chs[i])) {num = num * 10 + chs[i] - '0';} else {if (curChar != chs[i]) { // 当前char更新了,num重置为0sum += num;if (sum >= idx) {return curChar;}num = 0; // 关键:遇到新字符,其后续数字计数从0开始}curChar = chs[i];}}return sum + num > idx ? curChar : 0;}}
在有序但含有空的数组中查找字符串

思路:
- 二分查找。关注两种情况,一种是相等的情况如何处理,一种是 strs[mid] 为空的时候如何处理。 ```java package org.apache.java.codeviewguide.string;
/**
- 在有序但含有空的数组中查找字符串
- 给定一个字符串数组strs[],在strs中有些位置为null,但在不为null的位置上,
- 其字符串是按照字典顺序由小到大依次出现的。再给定一个字符串str,请返回str在strs中出现的最左的位置。 *
- 举例:
- strs = {null,”a”,null,”a”,null,”b”,null,”c”,null}
- str = “a’
返回“a”第一次出现的位置:1 */ public class OrderStrsFindStr { public static void main(String[] args) { // System.out.println(“b”.compareTo(“a”)); // 1
OrderStrsFindStr obj = new OrderStrsFindStr(); String[] strs = {“a”,”a”,null,”a”,null,”b”,null,”c”,null}; String str = “a”; System.out.println(obj.getIndex(strs, str)); }
public int getIndex(String[] strs, String str) { if (str == null) return -1; int len = strs.length; int left = 0, right = len - 1; int ret = -1; while (left <= right) { int mid = left + (right - left) / 2; if (strs[mid] != null && strs[mid] == str) { // mid值为str
ret = mid;right = mid - 1;
} else if (strs[mid] != null) { // strs[mid] != null,并且不等于 str
if (strs[mid].compareTo(str) >= 0) { // 往左走right = mid - 1;} else {left = mid + 1;}
} else { // 最复杂的 strs[mid] == null,此时朝那边走呢
// mid随机朝左右走,遇到不为null的字符串再判断更新left还是rightint p = mid;while (--p >= left && strs[p] == null) ;if (p >= left && strs[p].compareTo(str) >= 0) {ret = strs[p].equals(str) ? p : ret; // 处理相等情况right = mid - 1;} else {left = mid + 1;}
字符串的路径转换问题

思路:
- 根据结果先要知道这道题的本意是要从一张图中找到两个节点距离最近的所有路径集合。所以,第一步是要根据题目信息构建一张图,就需要知道每个节点可直达的所有节点;要知道最短路径,第二步就需要知道每个节点到起点的最短距离(通过图的广度优先遍历实现),第三部就是根据图的深度优先遍历,找到起点到终点的所有最短路径。
扩展:
- 这道题的思想非常广泛,比如地铁网、社交网等,都是找到两个节点的路径,并从中找出最优路径。
代码:
package org.kwang.java;import java.util.*;/*** 定两个字符串,记为start和to,再给定一个字符串列表list,list中一定包含to,list中没有重复字符串。* 所有的字符串都是小写的。规定start每次只能改变一个字符,最终的目标是彻底变成to,但是每次变成的新字符串必须在list中存在。* 请返回所有最短的变换路径。*/public class TwoStrsMinPaths {public static void main(String[] args) {TwoStrsMinPaths obj = new TwoStrsMinPaths();String start = "abc";String to = "cab";List<String> lists = new ArrayList<>(Arrays.asList("cab", "acc","cbc","ccc","cac","cbb","aab","abb"));obj.findMinPaths(start, to, lists);}public List<List<String>> findMinPaths(String start, String to, List<String> lists) {lists.add(start);// 1.找到每个str改变一个字符可达的所有nexts字符串Map<String, ArrayList<String>> nexts = getNexts(lists);System.out.println("============nexts数组===========");for (Map.Entry<String, ArrayList<String>> entry : nexts.entrySet()) {System.out.println(entry.getKey() + " : " + entry.getValue());}Map<String, Integer> distances = getMinDistances(start, nexts);System.out.println("============distances最短距离===========");for (Map.Entry<String, Integer> entry : distances.entrySet()) {System.out.println(entry.getKey() + " -> " + start + " : " + entry.getValue());}List<List<String>> res = new LinkedList<>();LinkedList<String> pathList = new LinkedList<>();getAllShortestPaths(start, to, nexts, distances, pathList, res);System.out.println("============所有最短距离===========");for (List<String> list : res) {System.out.println(list);}return res;}/*** 找到从start到to的所有最短路径(图的深度优先遍历)* @param cur* @param to* @param nexts* @param distances* @param pathList* @param res*/private void getAllShortestPaths(String cur, String to, Map<String, ArrayList<String>> nexts,Map<String, Integer> distances, LinkedList<String> pathList, List<List<String>> res) {pathList.add(cur);if (to.equals(cur)) {res.add(new LinkedList<>(pathList));}for (String str : nexts.get(cur)) {if (distances.get(str) == distances.get(cur) + 1) {getAllShortestPaths(str, to, nexts, distances, pathList, res);}}pathList.pollLast();}/*** 找到每个str到start节点的最短距离(图的广度优先遍历)* @param start* @param nexts* @return*/private Map<String, Integer> getMinDistances(String start, Map<String, ArrayList<String>> nexts) {Map<String, Integer> distances = new HashMap<>();distances.put(start, 0);Queue<String> queue = new LinkedList<>();queue.offer(start);// 记录访问过的节点Set<String> set = new HashSet<>();set.add(start);while (!queue.isEmpty()) {String cur = queue.poll();for (String str : nexts.get(cur)) {if (!set.contains(str)) {queue.add(str);distances.put(str, distances.get(cur) + 1);set.add(str);}}}return distances;}/*** 找打每个str可变换的nexts字符串集合* @param lists* @return*/private Map<String, ArrayList<String>> getNexts(List<String> lists) {Set<String> dict = new HashSet<>(lists);Map<String, ArrayList<String>> nexts = new HashMap<>();for (int i = 0; i < lists.size(); i++) {nexts.put(lists.get(i), getNext(lists.get(i), dict));}return nexts;}private ArrayList<String> getNext(String word, Set<String> dict) {ArrayList<String> list = new ArrayList<>();char[] chs = word.toCharArray();for (char ch = 'a'; ch < 'z'; ch++) {for (int i = 0; i < chs.length; i++) {if (chs[i] != ch) {char tmp = chs[i];chs[i] = ch;if (dict.contains(String.valueOf(chs))) {list.add(String.valueOf(chs));}chs[i] = tmp;}}}return list;}private void test() {HashSet<String> dict = new HashSet<>();dict.add("abc");dict.add("acc");String word = "abc";char[] chs = word.toCharArray();chs[1] = 'c';System.out.println("chs = " + String.valueOf(chs));System.out.println(dict.contains(String.valueOf(chs)));System.out.println(dict.contains(word));}}
树
二叉树中和为指定值的路径问题
思路:
- 参考“未排序数组和为给定值的最长子数组长度”,树中从根节点出发的每一条路径相当于一个数组,数组 s[i] 的定义就是树中的层级 level 树,左右节点属于同一级 level。确定了解决思路,然后通过树的遍历(先序(yes)/中序/后序)方式遍历树。(树的问题始终都要进行遍历)
扩展:
- 是否存在和为指定值的路径;
- 打印和为指定值的所有路径/最长路径;
- 路径从根节点开始或者可以跨越根节点;

二叉树的按层打印和ZigZag打印
思路:
按层打印:
- BFS两层遍历。常规方式是使用queue两层遍历,外层判断queue是否空,内部while判断queue的层级size元素是否打印完。(因为要打印层号,遍历过程中要记录当前遍历属于哪一层。)
- BFS一层遍历。用变量 last 记录当前遍历层的最右节点,nLast 表示下一层遍历的最右节点,当遍历的节点 cur == last 时表示一层元素遍历结束,然后 last = nLast 开始下一层遍历。
按ZigZag打印:
- BFS两层遍历。和层打印思路一类似,无非就是根据每一层规则确定先添加最左还是最右节点,所以这里选择使用双端队列,左到右遍历添加节点到队列尾部,先添加右孩子再添加左孩子,右到左遍历添加节点到队列头部,先添加左孩子再添加右孩子。
二叉树中某个节点的后继节点
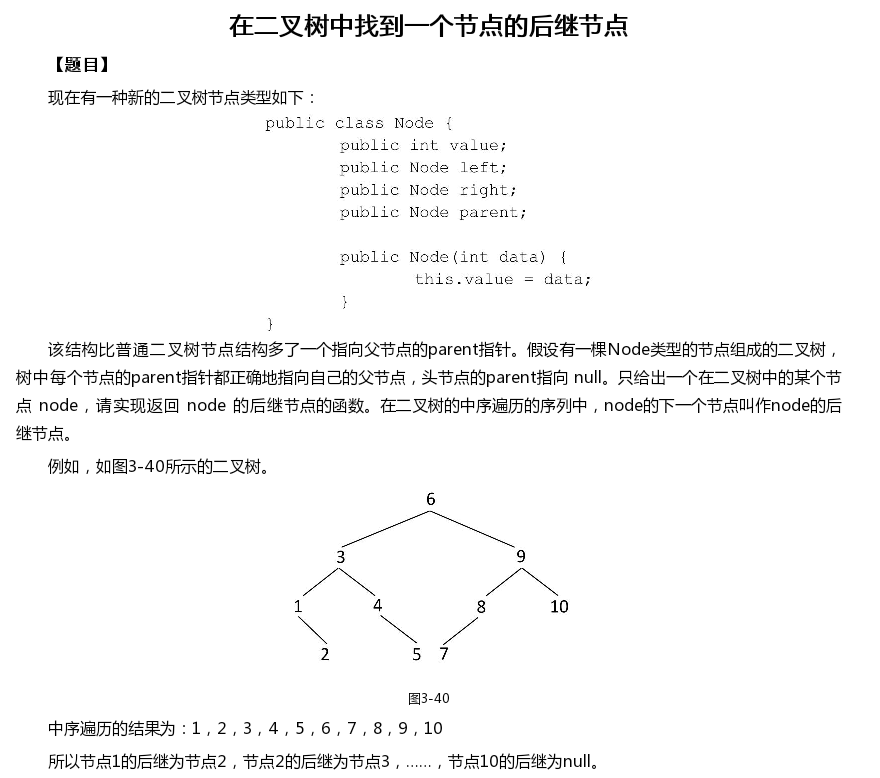
代码:
/*** 二叉树中序遍历下某个节点的后继节点*/public class TreeNextNode {private static class Node {int data;Node left;Node right;Node parent;public Node(int data) {this.data = data;}}public Node getNextNode(Node node) {if (node == null)return null;if (node.right != null) { // 获取右孩子的最左节点return mostLeftNode(node.right);} else {// 没有右子树,则判断node和parent的关系// 如果node为parent的left节点,则返回parent节点Node parent = node.parent;while (parent != null && node != parent.left) {node = parent;parent = node.parent;}return parent;}}public Node mostLeftNode(Node node) {if (node == null)return null;while (node.left != null) {node = node.left;}return node;}public static void main(String[] args) {Node node6 = new Node(6), node3 = new Node(3), node9 = new Node(9);Node node1 = new Node(1), node4 = new Node(4), node8 = new Node(8), node10 = new Node(10);Node node2 = new Node(2), node5 = new Node(5), node7 = new Node(7);node6.left = node3; node6.right = node9;node3.left = node1; node3.right = node4;node9.left = node8; node9.right = node10;node1.right = node2;node4.right = node5;node8.left = node7;node3.parent = node6; node9.parent = node6;node1.parent = node3; node4.parent = node3;node8.parent = node9; node10.parent = node9;node2.parent = node1; node5.parent = node4;node7.parent = node8;TreeNextNode obj = new TreeNextNode();Node ret = obj.getNextNode(node10);System.out.println(ret == null? 0: ret.data);}}
二叉树中两个节点的最近公共祖先

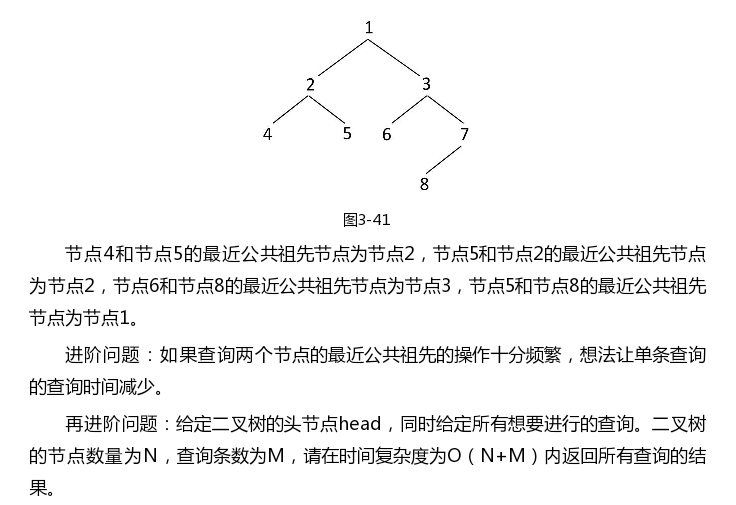
代码:
package org.kwang.java;import java.util.ArrayList;import java.util.HashMap;import java.util.List;import java.util.Map;/*** 原问题:给定一棵二叉树的头节点head,以及这棵树中的两个节点o1和o2,请返回o1和o2的最近公共祖先节点。* 进阶问题:如果查询两个节点的最近公共祖先的操作十分频繁,想法让单条查询的查询时间减少。* (todo)再进阶问题:给定二叉树的头节点head,同时给定所有想要进行的查询。* 二叉树的节点数量为N,查询条数为M,请在时间复杂度为O(N+M)内返回所有查询的结果。*/public class TreeFindNearestParent {public static void main(String[] args) {TreeFindNearestParent obj = new TreeFindNearestParent();/*** 1* / \* 2 3* / \ / \* 4 5 6 7* /* 8*/TreeNode o1 = new TreeNode(1), o2 = new TreeNode(2), o3 = new TreeNode(4);TreeNode o4 = new TreeNode(4), o5 = new TreeNode(5), o6 = new TreeNode(6), o7 = new TreeNode(7);TreeNode o8 = new TreeNode(8);o1.left = o2; o1.right = o3;o2.left = o4; o2.right = o5;o3.left = o6; o3.right = o7;o7.left = o8;TreeNode ret = obj.findNearestParent(o1, o4, o5);System.out.println(ret.val);System.out.println("=================");TreeFindNearestParent obj2 = new TreeFindNearestParent(o1);TreeNode ret2 = obj2.frequentQuery(o1,o4,o8);System.out.println(ret2 != null ? ret2.val : null);// 特殊情况:其中一个为根节点System.out.println(obj2.frequentQuery(o1, o1,o8).val);// 特殊情况:节点不在树中TreeNode ret3 = obj2.frequentQuery(o1, o8, new TreeNode(8));System.out.println( ret3 != null ? ret3.val : null);}/*** 原问题:找到二叉树中两个节点的最近公共祖先* @param head* @param node1* @param node2* @return*/public TreeNode findNearestParent(TreeNode head, TreeNode node1, TreeNode node2) {if (head == null || head == node1 || head == node2) {return head;}TreeNode left = findNearestParent(head.left, node1, node2);TreeNode right = findNearestParent(head.right, node1, node2);System.out.println("node = " + head.val + "; left = " + (left != null ? left.val : null) +"; right = " + (right != null ? right.val : null));if (left != null && right != null) {return head;}return left != null ? left : right;}/*** 进阶问题:频繁查找二叉树中两个节点的最近公共祖先。* 思路:* - 存储每个节点的父亲节点* - 先向上遍历得到node1的所有父亲节点,然后遍历node2的父亲节点,遇到相同的则返回。* 扩展:* - 记录父亲节点可以找到根节点到叶子节点的所有路径* @param node1* @param node2* @return*/public TreeNode frequentQuery(TreeNode head, TreeNode node1, TreeNode node2) {if (head == null || head == node1 || head == node2) {return head;}if (!(isTreeNode(head, node1) && isTreeNode(head, node2))) {return null;}List<TreeNode> parentList = new ArrayList<>();// 统计node1的所有父亲节点while (parentMap.containsKey(node1)) {node1 = parentMap.get(node1);if (node1 != null) parentList.add(node1);}while (!parentList.contains(node2)) {node2 = parentMap.get(node2);}return node2;}Map<TreeNode, TreeNode> parentMap;public TreeFindNearestParent() {}/*** 初始化map* @param head*/public TreeFindNearestParent(TreeNode head) {parentMap = new HashMap<>();if (head != null) {parentMap.put(head, null);}setParent(head);}private void setParent(TreeNode head) {if (head == null) {return;}if (head.left != null) {parentMap.put(head.left, head);}if (head.right != null) {parentMap.put(head.right, head);}setParent(head.left);setParent(head.right);}/*** 判断一个节点是否是树中的节点* @param head* @param node* @return*/public boolean isTreeNode(TreeNode head, TreeNode node) {if (head == null) {return false;}if (head == node) {return true;}boolean left = isTreeNode(head.left, node);boolean right = isTreeNode(head.right, node);return left == true ? true : right;}}
数组和矩阵
未排序正数数组和为指定值的最长子数组长度
思路:
- 思路一:left 指针从 0 开始,right 也从 0 位置开始作为窗口的右边界,两层遍历,时间复杂度为 O(n^2)。
- 思路二:sum 为 arr[left, right] 数组区间的和,left 和 right 都从 0 开始,判断 sum 和目标和 k 的大小,来决定 left 还是 right 的移动。如果 sum = k,记录 len,left + 1,
扩展:
- 和为指定值的所有子数组/最长子数组
- 数组中数据有负数问题又如何处理?

未排序数组和为给定值的最长子数组
思路:
- 用 s[i] 表示 arr[0, i] 的元素和,arr[i, j] 区间的元素和为 s[j] - s[i-1]。如果历史 s[n] 数组中存在 (s[i] - k) 值的位置,说明该区间段有和为 k 的子数组。
例:数组 arr = [10,1,0,-1,2,-2,0,-1,1,2],和 k = 2。
| idx | s[i] | map-key | map-value (s出现的位置) |
备注 |
|---|---|---|---|---|
| 0 | 10 | 10 | 0 | |
| 1 | 11 | 11 | 1 | |
| 2 | 11 | 不更新,因为是求最长数组 | ||
| 3 | 10 | 10 | 3 | |
| 4 | 12 | 记录 len | ||
| 5 | 10 | 不更新 | ||
| 6 | 10 | 不更新 | ||
| 7 | 9 | 9 | 7 | |
| 8 | 10 | 不更新 | ||
| 9 | 12 | 记录 len |




