遍历问题

105-从前序与中序遍历序列构造二叉树

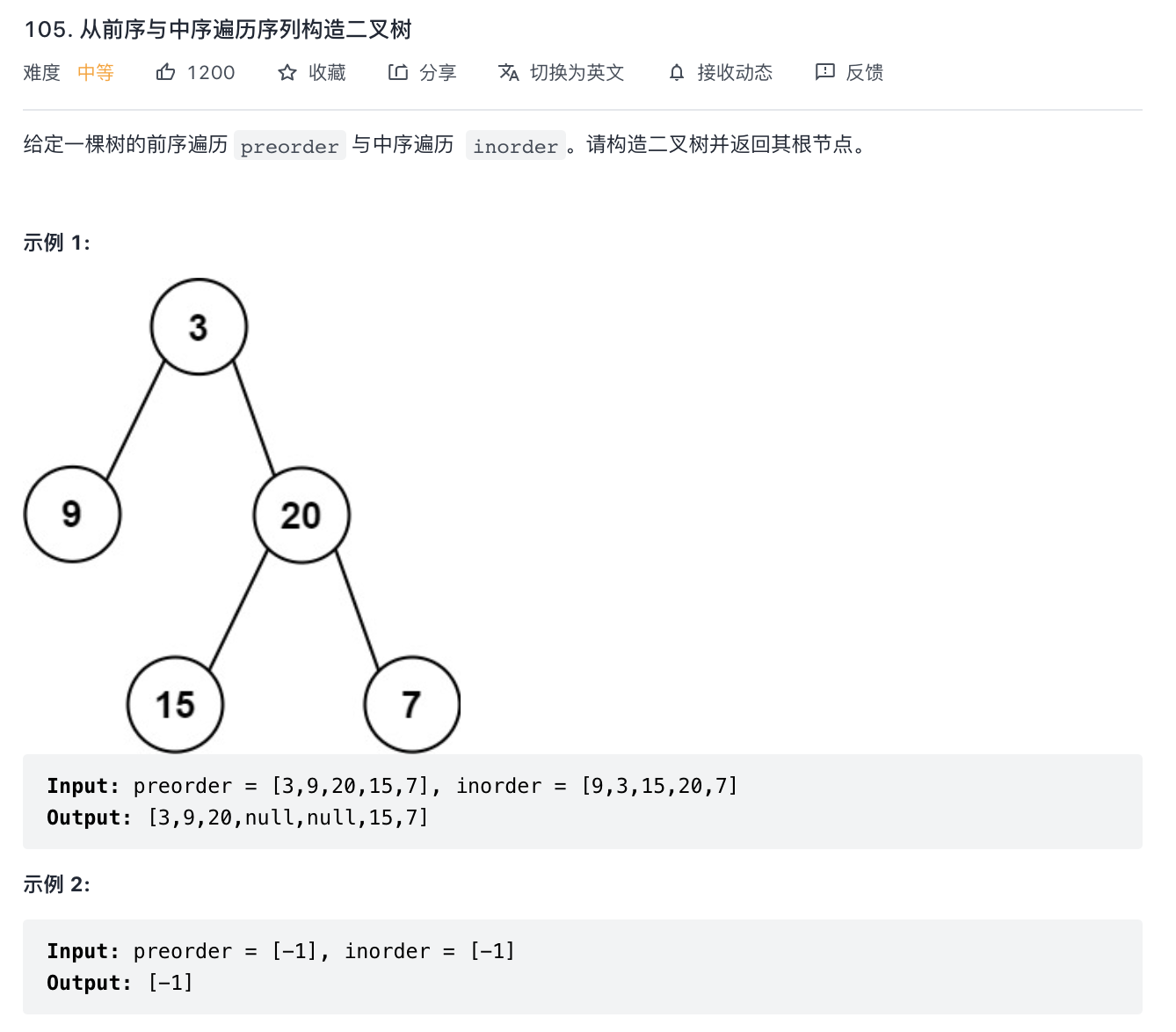
image.png
题意分析：

  • 根据树的遍历重构二叉树。

解题思路：

  • 先根据 preorder 遍历找到 root 节点，找到 root 节点在 inorder 的索引位置 idx，然后递归构造左右子树（难点在于如何根据 idx 分隔左右子树区间）。

注意点：
扩展：
代码：

  1.         public TreeNode buildTree(int[] preorder, int[] inorder) {
  2.             return build(preorder, 0, preorder.length - 1, inorder, 0, inorder.length - 1);
  3.         }
  5.         private TreeNode build(int[] preorder, int preStart, int preEnd, int[] inorder, int inStart, int inEnd) {
  6.             // 递归结束条件
  7.             if (preStart > preEnd) {
  8.                 return null;
  9.             }
  10.             System.out.println(Arrays.toString(preorder) + ": prestart=" + preStart + "; preend=" + preEnd);
  11.             System.out.println(Arrays.toString(inorder) + " instart=" + inStart +"; inend=" + inEnd);
  12.             System.out.println();
  14.             int rootVal = preorder[preStart];
  16.             // 记录中序遍历中rootVal 对应的位置
  17.             int idx = -1;
  19.             // 这里每次递归调用时都会重复遍历inorder 数组，可以通过 HashMap 保持 val 对应的 idx 信息
  20.             for (int i = inStart; i <= inEnd; i++) {
  21.                 if (inorder[i] == rootVal) {
  22.                     idx = i;
  23.                     break;
  24.                 }
  25.             }
  27.             // 根据先序遍历找到新树的 root 节点
  28.             TreeNode root = new TreeNode(rootVal);
  29.             // left_len = idx - inStart
  30.             root.left = build(preorder, preStart + 1, preStart + (idx - inStart), inorder, inStart, idx - 1);
  31.             root.right = build(preorder, preStart + (idx - inStart) + 1, preEnd, inorder, idx + 1, inEnd);
  33.             if (root.left != null && root.right != null)
  34.                 System.out.println("root=" + root.val + "; root.left=" + root.left.val + "; root.right=" + root.right.val);
  35.             return root;
  36.         }

106-从中序与后序遍历序列构造二叉树

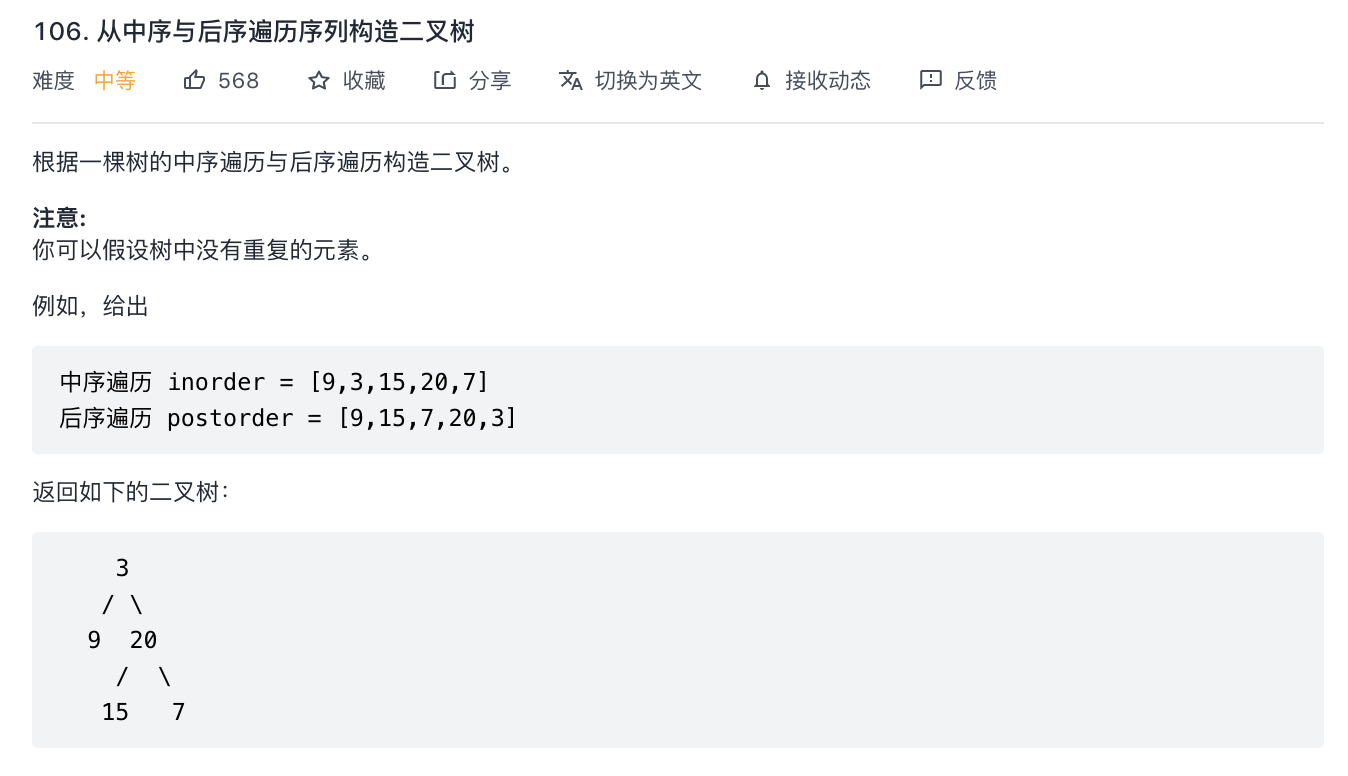
image.png
题意分析：

  • 和 105 题目差不多，条件序列不同而已。

解题思路：

  • 先根据 postorder 遍历找到 root 节点，找到 root 节点在 inorder 的索引位置 idx，然后递归构造左右子树（难点在于如何根据 idx 分隔左右子树区间）。

注意点：
扩展：
代码：

  1.     public TreeNode buildTree(int[] inorder, int[] postorder) {
  2.         return build(inorder, 0, inorder.length - 1, postorder, 0, postorder.length - 1);
  3.     }
  5.     private TreeNode build(int[] inorder, int inStart, int inEnd, int[] postorder, int postStart, int postEnd) {
  6.         if (postStart > postEnd) {
  7.             return null;
  8.         }
  9.         System.out.println(Arrays.toString(inorder) + ": inStart=" + inStart + "; inEnd=" + inEnd);
  10.         System.out.println(Arrays.toString(postorder) + " postStart=" + postStart +"; postEnd=" + postEnd);
  11.         System.out.println();
  13.         int rootVal = postorder[postEnd];
  15.         // 记录中序遍历中rootVal 对应的位置
  16.         int idx = -1;
  17.         for (int i = inStart; i <= inEnd; i++) {
  18.             if (inorder[i] == rootVal) {
  19.                     idx = i;
  20.                     break;
  21.             }
  22.         }
  24.         // 根据先序遍历找到新树的 root 节点
  25.         TreeNode root = new TreeNode(rootVal);
  26.         root.left = build(inorder, inStart, idx - 1, postorder, postStart, postStart + (idx - inStart) - 1);
  27.         root.right = build(inorder, idx + 1, inEnd, postorder, postStart + (idx - inStart), postEnd - 1);
  29.         System.out.println("root=" + root.val + "; root.left=" + root.left + "; root.right=" + root.right);
  30.         if (root.left != null && root.right != null)
  31.             System.out.println("root=" + root.val + "; root.left=" + root.left.val + "; root.right=" + root.right.val);
  32.         return root;
  33.     }

二叉树的先序遍历

代码：

  1.     public List<Integer> preorderTraversal(TreeNode root) {
  2.         List<Integer> res = new ArrayList<>();
  3.         preorder(root, res);
  4.         return res;
  5.     }
  7.     public void preorder(TreeNode root, List res) {
  8.         if (root == null) {
  9.             return;
  10.         }
  11.         res.add(root.val);
  12.         preorder(root.left, res);
  13.         preorder(root.right, res);
  14.     }
  16.     public List<Integer> preorderTraversal2(TreeNode root) {
  17.         List<Integer> res = new ArrayList<>();
  18.         Deque<TreeNode> stack = new LinkedList<>();
  19.       if (root == null) {
  20.            return res;
  21.       }
  22.         stack.push(root);
  23.         while (!stack.isEmpty()) {
  24.             TreeNode node = stack.pop();
  25.             res.add(node.val);
  27.             if (node.right != null) {
  28.                 stack.push(node.right);
  29.             }
  31.             if (node.left != null) {
  32.                 stack.push(node.left);
  33.             }
  34.         }
  35.         return res;
  36.     }

94-二叉树的中序遍历

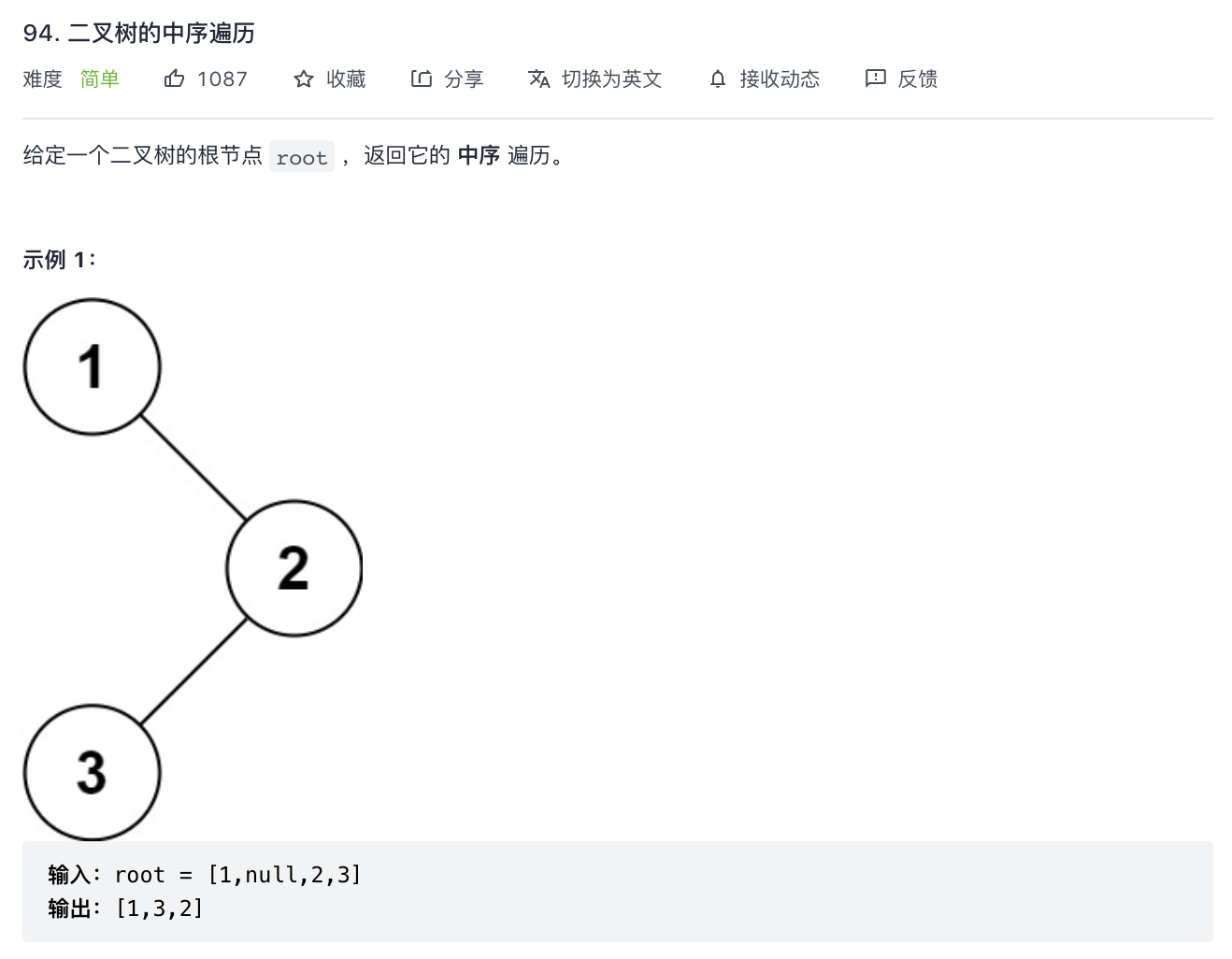
image.png
代码：

  1.     /**
  2.      *  递归思路：
  3.      *    1、递归退出条件
  4.      *    2、递归体
  5.      */
  6.         public List<Integer> inorderTraversal(TreeNode root) {
  7.             List<Integer> res = new ArrayList<>();
  8.             inorder(root, res);
  9.             return res;
  10.         }
  12.     private void inorder(TreeNode root, List<Integer> res) {
  13.         if (root == null) {
  14.             return;
  15.         }
  16.         inorder(root.left, res);
  17.         res.add(root.val);
  18.         inorder(root.right, res);
  19.     }
  21.     /**
  22.      * 非递归思路：
  23.      *  1、手动维护栈，什么时候进栈，什么时候出栈
  24.      * @param root
  25.      * @return
  26.      */
  27.     public List<Integer> inorderTraversal2(TreeNode root) {
  28.         List<Integer> res = new ArrayList<>();
  29.         Deque<TreeNode> stack = new LinkedList<>();
  30.         while (root != null || !stack.isEmpty()) {
  31.             while (root != null) {
  32.                 stack.push(root);
  33.                 root = root.left;
  34.             }
  35.             TreeNode node = stack.pop();
  36.             res.add(node.val);
  37.             root = node.right;
  38.         }
  39.         return res;
  40.     }

二叉树的后序遍历

代码：

  1.     public List<Integer> postorderTraversal(TreeNode root) {
  2.         List<Integer> res = new ArrayList<>();
  3.         postorder(root, res);
  4.         return res;
  5.     }
  7.     public void postorder(TreeNode root, List res) {
  8.         if (root == null) {
  9.             return;
  10.         }
  11.         postorder(root.left, res);
  12.         postorder(root.right, res);
  13.         res.add(root.val);
  14.     }
  16.     public List<Integer> postorderTraversal2(TreeNode root) {
  17.         List<Integer> res = new ArrayList<>();
  18.         Deque<TreeNode> stack = new LinkedList<>();
  19.         TreeNode pre = null; // 用于记录上一次访问的节点
  20.         while (root != null || !stack.isEmpty()) {
  21.             while (root != null) {
  22.                 stack.push(root);
  23.                 root = root.left;
  24.             }
  25.             TreeNode node = stack.pop();
  26.             if (node.right != null) {
  27.                 stack.push(node);
  28.                 root = node.right;
  29.             } else if (node.right == null || node.right == pre){
  30.                 res.add(node.val);
  31.                 pre = node;
  32.                 root = null;
  33.             }
  34.         }
  35.         return res;
  36.     }

102-二叉树的层序遍历

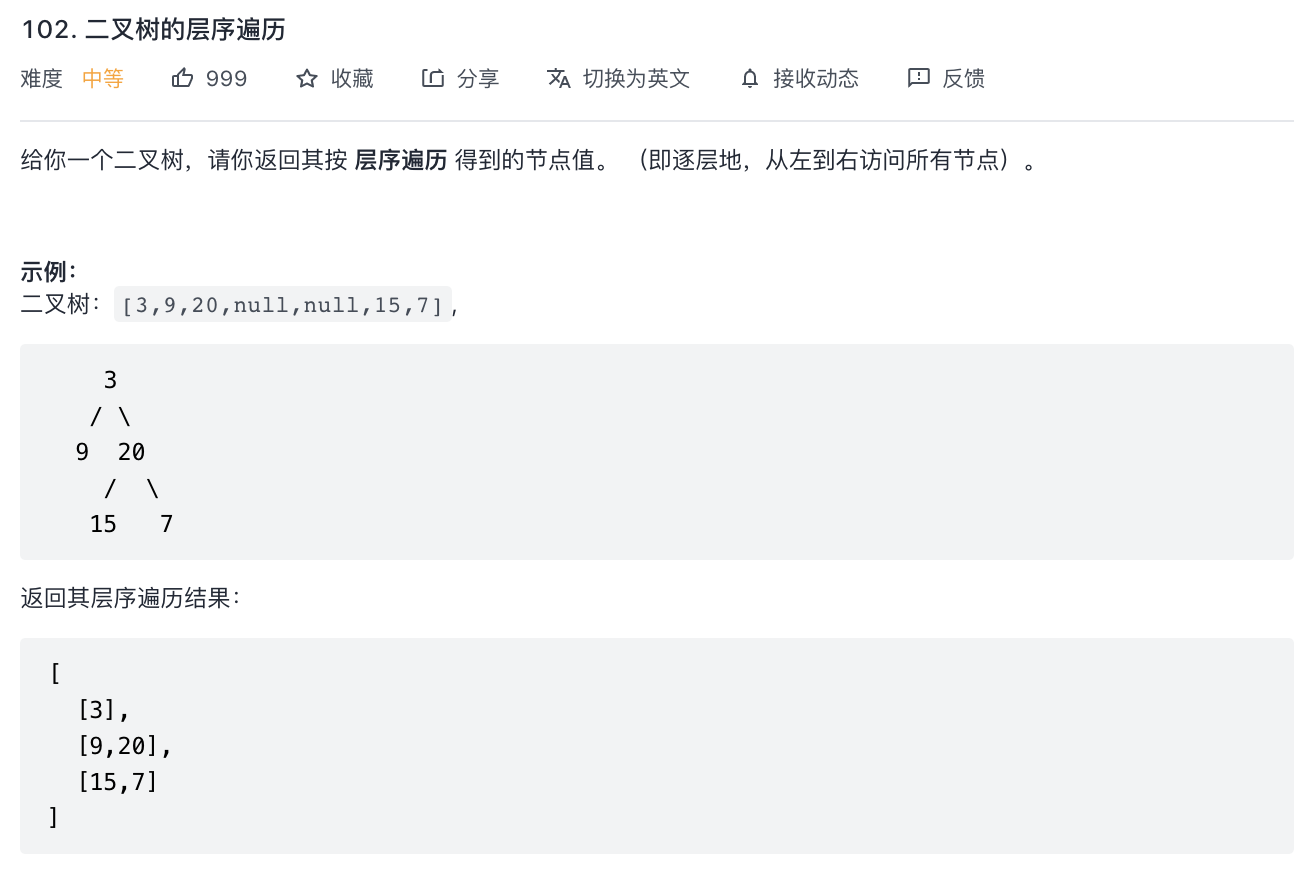
image.png
代码：

  1.     public List<List<Integer>> levelOrder(TreeNode root) {
  2.         List<List<Integer>> res = new ArrayList<>();
  3.         if (root == null) {
  4.             return res;
  5.         }
  6.         Queue<TreeNode> queue = new LinkedList<>();
  7.         queue.offer(root);
  8.         while (!queue.isEmpty()) {
  9.             int size = queue.size();
  10.             List<Integer> list = new ArrayList<>();
  11.             // 逐层记录元素
  12.             while (size > 0) {
  13.                 TreeNode node = queue.poll();
  14.                 list.add(node.val);
  15.                 if (node.left != null) {
  16.                     queue.offer(node.left);
  17.                 }
  18.                 if (node.right != null) {
  19.                     queue.offer(node.right);
  20.                 }
  21.                 size--;
  22.             }
  23.             // 一层元素遍历完了添加到 res 中
  24.             res.add(list);
  25.         }
  26.         return res;
  27.     }

路径问题

1104-二叉树寻路

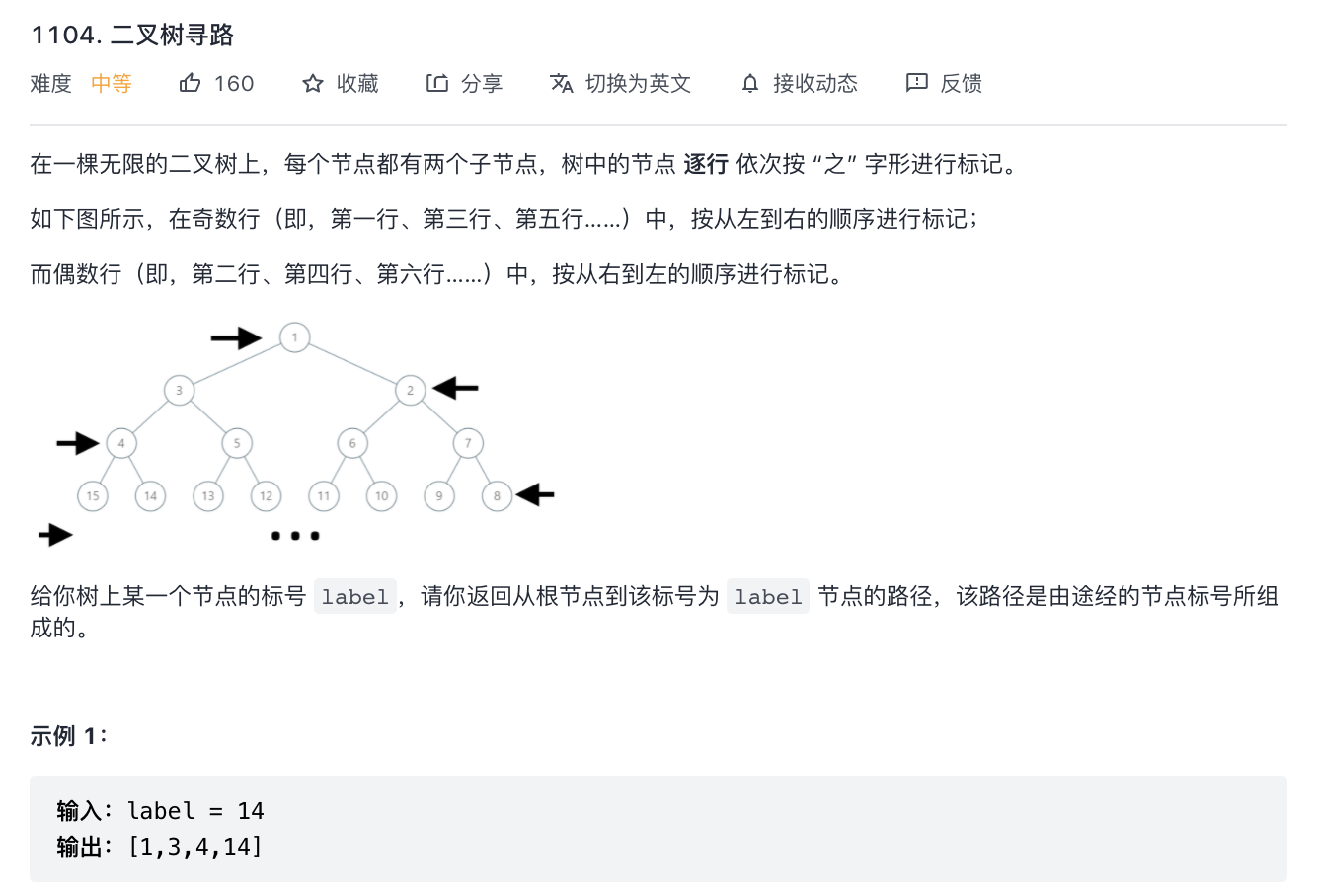
image.png
题意分析：

  • 打印树根节点到 label 的路径，只不过是树奇偶层级数据进行了反向。

解题思路：

  • 按层级遍历完全二叉树，根据对称关系对树进行处理。

注意点：
扩展：
代码：

  1. /**
  2.      * 解题思路
  3.      *  特点：完全二叉树
  4.      *    1、每一行的元素区间为 [2^(level-1), 2^level -1]
  5.      * @param label
  6.      * @return
  7.      */
  8.     public List<Integer> pathInZigZagTree(int label) {
  9.         // 根据 label 得到所在行数
  10.         int level = 1;
  11.         // 每一行的最大元素为 2^(row) - 1
  12.         while (label > (Math.pow(2, level) - 1)) {
  13.             level++;
  14.         }
  16.         // 因为偶数行是反着的，所以在寻路前先和对称元素交换，在处理偶数行时再交换过来。
  17.         if (level % 2 == 0) {
  18.             label = (int)(Math.pow(2, level - 1) + Math.pow(2, level)) - 1 -label;
  19.         }
  21.         List<Integer> path = new ArrayList<>();
  22.         while (level > 0) {
  23.           // 奇偶行分别处理，奇数行正常处理，偶数行对称处理
  24.             if (level % 2 == 0) {
  25.               // 拿到对称的元素。（对称两个元素和是固定的）
  26.               int val = (int)(Math.pow(2, level - 1) + Math.pow(2, level)) - 1 -label;
  27.               path.add(val);
  28.             } else {
  29.                 path.add(label);
  30.             }
  31.             // label 往父节点走一次，并且行数减 1
  32.             label = label / 2;
  33.             level--;
  34.         }
  35.         Collections.reverse(path);
  36.         return path;
  37.     }

257-二叉树的所有路径

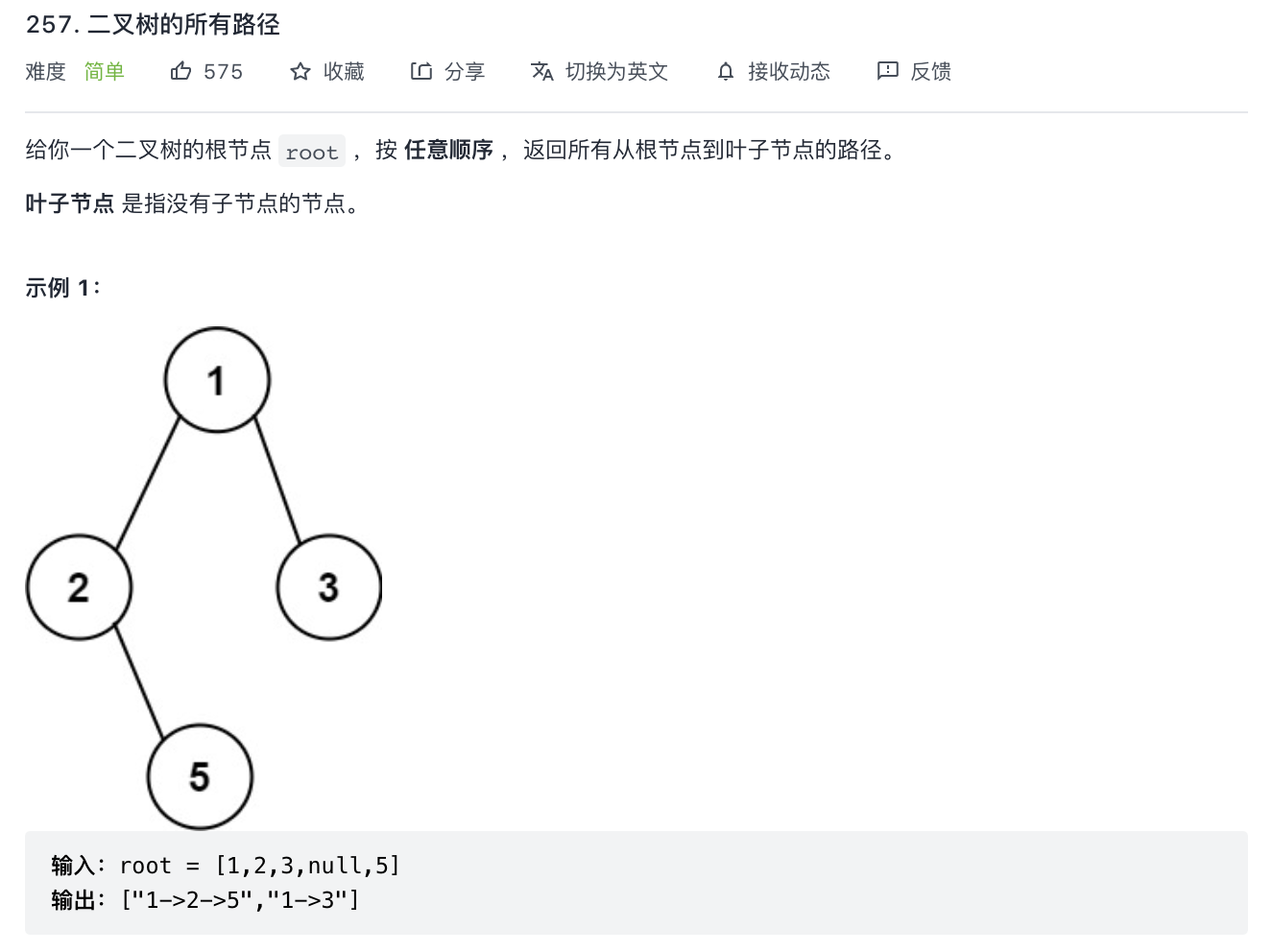
image.png
题意分析：

  • 打印数的所有路径，显然是要遍历树。

解题思路：

  • dfs 深度遍历，遍历到树节点开始回溯。

注意点：
扩展：

  • 能否使用 bfs 广度遍历实现？

代码：

  1.     /**
  2.      * dfs深度遍历 + 回溯思想（找完一个往回找）
  3.      */
  4.     List<List<Integer>> res = new LinkedList<>();
  6.     public List<List<Integer>> binaryTreePaths(TreeNode root) {
  7.         LinkedList<Integer> path = new LinkedList<>();
  8.         dfs(root, path);
  9.         return res;
  10.     }
  12.     public void dfs(TreeNode root, LinkedList path) {
  13.         if (root == null) {
  14.             return;
  15.         }
  16.         path.offer(root.val);
  17.         if (root.left == null && root.right == null) {
  18.             res.add(new LinkedList<>(path));
  19. //            return;
  20.         }
  21.         dfs(root.left, path);
  22.         dfs(root.right, path);
  23.         path.pollLast();
  24.     }

112-路径总和 I

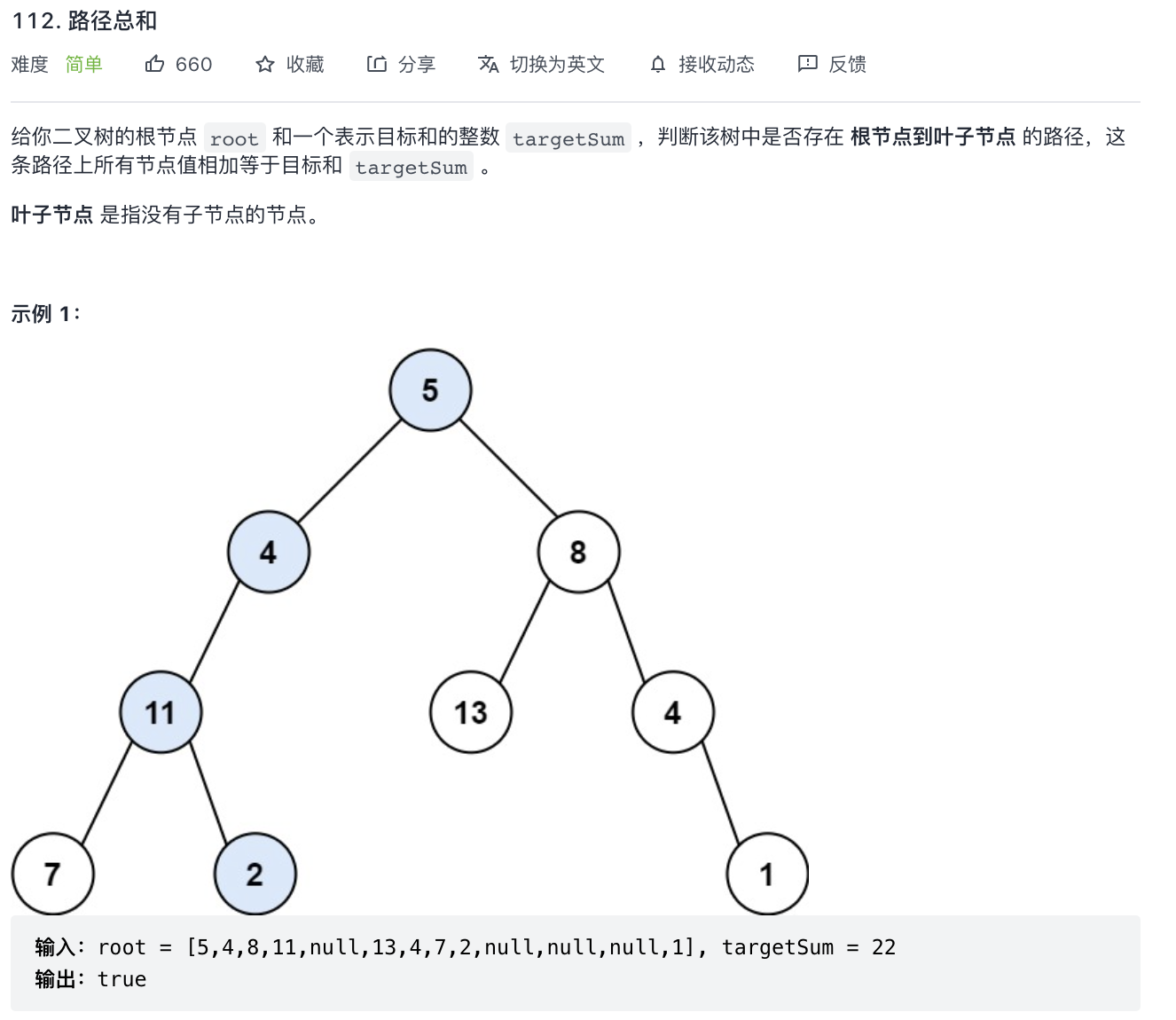
image.png
题意分析：

  • 判断是否存在从根节点到叶子节点存在和为 sum 的路径。

解题思路：

  • dfs 递归遍历，不断减去节点值递归。
  • 层序遍历，记录每一层所有节点的和，直到叶子节点，判断是否存在和为 sum 的叶子节点。

注意点：
扩展：

  • 如何输出所有路径？

代码：

  1.     /**
  2.      * 先序遍历。
  3.      *
  4.      * 思考：如果存在路径，如何打印出路径？
  5.      *
  6.      * @param root
  7.      * @param sum
  8.      * @return
  9.      */
  10.     public boolean hasPathSum(TreeNode root, int sum) {
  11.         // base case
  12.         if (root == null) {
  13.             return false;
  14.         }
  15.         sum -= root.val;
  16.         if (root.left == null && root.right == null && sum == 0) {
  17.             return true;
  18.         }
  19.         boolean left = hasPathSum(root.left, sum);
  20.         boolean right = hasPathSum(root.right, sum);
  21.         return left || right;
  22.     }

113-路径总和 II

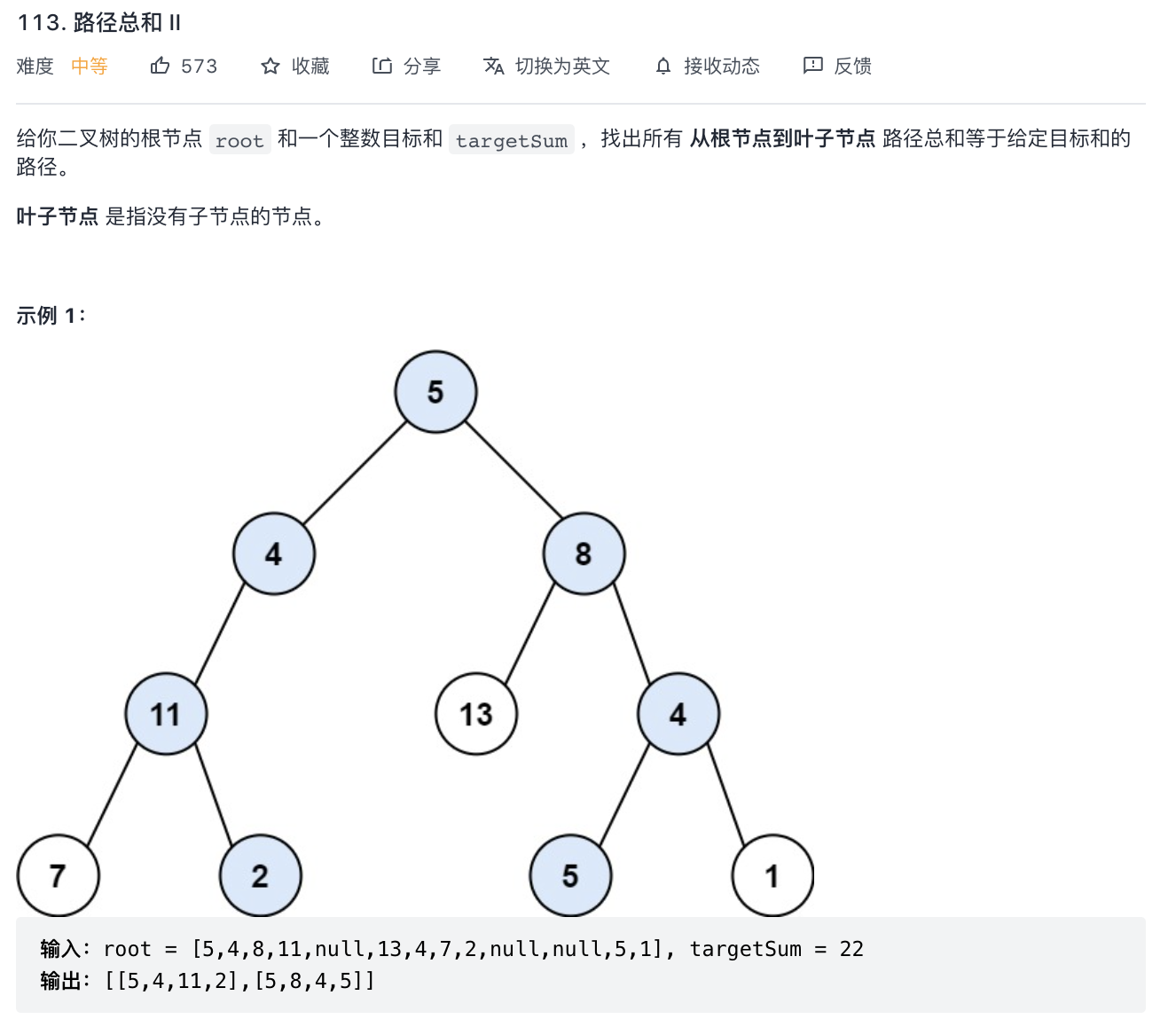
image.png
题意分析：

  • 输出所有和为 sum 的路径，该路径从根节点到叶子节点。

解题思路：

  • dfs。路径问题建议 dfs 算法，可以结合回溯思想遍历到每个叶子节点。
  • bfs（层序遍历）。记录每一层节点中到达该节点的路径总和，并且还要记录其父亲节点。

注意点：

  • bfs 思路要记录父亲节点，方便在找到节点后输出路径。

扩展：
代码：

  1.     // bfs
  2.     // 记录所有path路径
  3.     List<List<Integer>> res = new ArrayList<>();
  4.     // path:找到预期节点后向上父节点寻找（树特点：一个节点只有一个父亲节点）
  5.     Map<TreeNode, TreeNode> map = new HashMap<>();
  7.     public List<List<Integer>> pathSum2(TreeNode root, int targetSum) {
  8.         if (root == null) {
  9.             return res;
  10.         }
  11.         // 这两个队列元素是一一对应的
  12.         // 记录层序遍历节点（BFS思想）
  13.         Queue<TreeNode> queue = new LinkedList<>();
  14.         // 记录当前层级所有节点的和
  15.         Queue<Integer> sumQueue = new LinkedList<>();
  17.         queue.offer(root);
  18.         sumQueue.offer(root.val);
  19.         map.put(root, null);
  20.         while (!queue.isEmpty()) {
  21.             int size = queue.size();
  22.             while (size > 0) {
  23.                 TreeNode curr = queue.poll();
  24.                 int val = sumQueue.poll();
  26.                 if (curr.left == null && curr.right == null && val == targetSum) {
  27.                     getPath(curr);
  28.                 }
  30.                 if (curr.left != null) {
  31.                     queue.offer(curr.left);
  32.                     sumQueue.offer(val + curr.left.val);
  33.                     map.put(curr.left, curr);
  34.                 }
  36.                 if (curr.right != null) {
  37.                     queue.offer(curr.right);
  38.                     sumQueue.offer(val + curr.right.val);
  39.                     map.put(curr.right, curr);
  40.                 }
  41.                 size--;
  42.             }
  43.         }
  44.         return res;
  45.     }
  47.     /**
  48.      * 寻找父亲节点路径
  49.      * @param leaf
  50.      */
  51.     public void getPath(TreeNode leaf) {
  52.         List<Integer> list = new ArrayList<>();
  53.         while (leaf != null) {
  54.             list.add(leaf.val);
  55.             leaf = map.get(leaf);
  56.         }
  57.         Collections.reverse(list);
  58.         res.add(list);
  59.     }
  62.     // dfs
  63.     // 记录所有path路径
  64.     List<List<Integer>> res2 = new LinkedList<>();
  65.     public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
  66.         dfs(root, targetSum, new LinkedList());
  67.         return res2;
  68.     }
  70.     public void dfs(TreeNode root, int sum, LinkedList path) {
  71.         if (root == null) {
  72.             return;
  73.         }
  74.         sum -= root.val;
  75.         path.offer(root.val);
  76.         if (root.left == null && root.right == null && sum == 0) {
  77.             res2.add(new LinkedList<>(path));
  78.         }
  79.         dfs(root.left, sum, path);
  80.         dfs(root.right, sum, path);
  81.         path.pollLast();
  82.     }

437-路径总和 III

image.png
题意分析：

  • 输出和为 sum 的路径，该路径不一定包含根节点或叶子节点，只有和为 sum 的节点都可以，且不跨越根节点。

解题思路：

  • 结合路径总和II 解法，对所有节点递归调用 II 的逻辑，退出条件为 sum=0 即可。

注意点：

  • 递归的退出条件。

扩展：
代码：

  1. // 记录所有path路径
  2.     List<List<Integer>> res = new LinkedList<>();
  4.     public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
  5.         if (root == null) {
  6.             return res;
  7.         }
  8.         dfs(root, targetSum, new LinkedList<>());
  10.         // 由于总和不一定包括根节点，对左右孩子节点也要递归遍历
  11.         pathSum(root.left, targetSum);
  12.         pathSum(root.right, targetSum);
  13.         return res;
  14.     }
  16.     public void dfs(TreeNode root, int sum, LinkedList path) {
  17.         if (root == null) {
  18.             return;
  19.         }
  20.         sum -= root.val;
  21.         path.offer(root.val);
  22.         // 和路径总和II 问题的区别是这里不用判断节点是否是叶子节点
  23.         if (sum == 0) {
  24.             res.add(new LinkedList<>(path));
  25.         }
  26.         dfs(root.left, sum, path);
  27.         dfs(root.right, sum, path);
  28.         path.pollLast();
  29.     }

687-最长同值路径(?)

image.png
题意分析：

  • 树中最长的包含相同 val 的节点，路径可以包含根节点。

解题思路：

  • dfs 后序遍历，计算每个节点的左右最大同值数量。

注意点：
扩展：
代码：

  1.     int res = 0;
  2.     public int longestUnivaluePath(TreeNode root) {
  3.         longestPath(root);
  4.         return res;
  5.     }
  7.     public int longestPath(TreeNode root){
  8.         if (root == null) {
  9.             return 0;
  10.         }
  11.         int left = longestPath(root.left);
  12.         int right = longestPath(root.right);
  14.         if (root.left != null && root.val == root.left.val) {
  15.             left++;
  16.         } else {
  17.             left = 0;
  18.         }
  19.         if (root.right != null && root.val == root.right.val) {
  20.             right++;
  21.         } else {
  22.             right = 0;
  23.         }
  24.         // 打印当前root节点的左右子树值都最好。
  25. //        System.out.println(root.val + ": left = " + left +"; right = " + right);
  27.         // 如果根节点的左右子树res都为1，则表示根节点和左右节点的值 val 相等。
  28.         res = Math.max(res, left + right);
  30.         // 返回左右子树的最长同值路径
  31.         return Math.max(left, right);
  32.     }

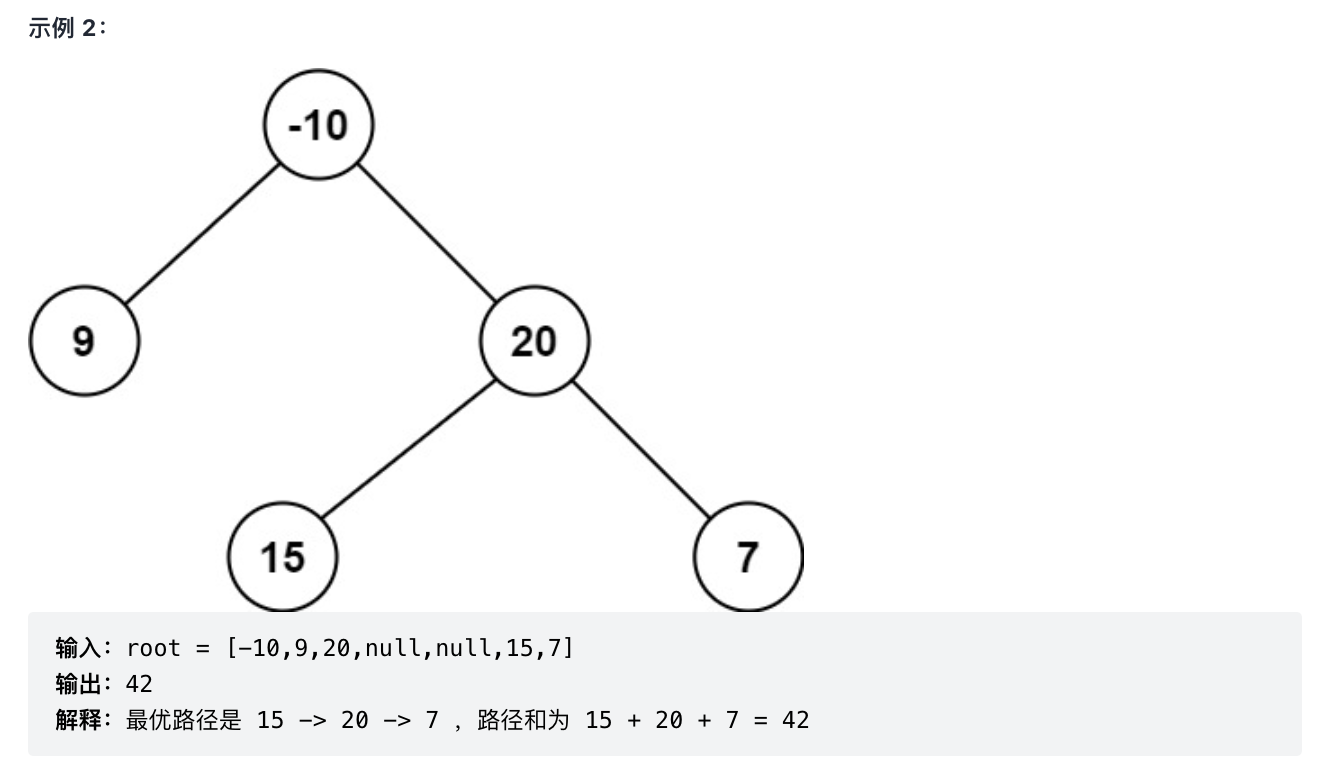
124-二叉树中的最大路径和(?)

image.png
image.png
题意分析：

  • 二叉树中节点包含负数情况下最大的路径和，可以经过或不经过根节点。

解题思路：

  • dfs 遍历分别计算每个节点的左右子树的最大路径和。

注意点：
扩展：
代码：

  1.     int maxSum = Integer.MIN_VALUE;
  2.     public int maxPathSum(TreeNode root) {
  3.         maxPath(root);
  4.         return maxSum;
  5.     }
  7.     public int maxPath(TreeNode root) {
  8.         if (root == null) {
  9.             return 0;
  10.         }
  11.         // 如果某个路径小于0，则改路径是无增益路径
  12.         int left = Math.max(maxPath(root.left), 0);
  13.         int right = Math.max(maxPath(root.right), 0);
  14.         System.out.println(root.val + ": left = " + left +"; right = " + right);
  15.         maxSum = Math.max(maxSum, left + right + root.val);
  16.         return root.val + Math.max(left, right);
  17.     }

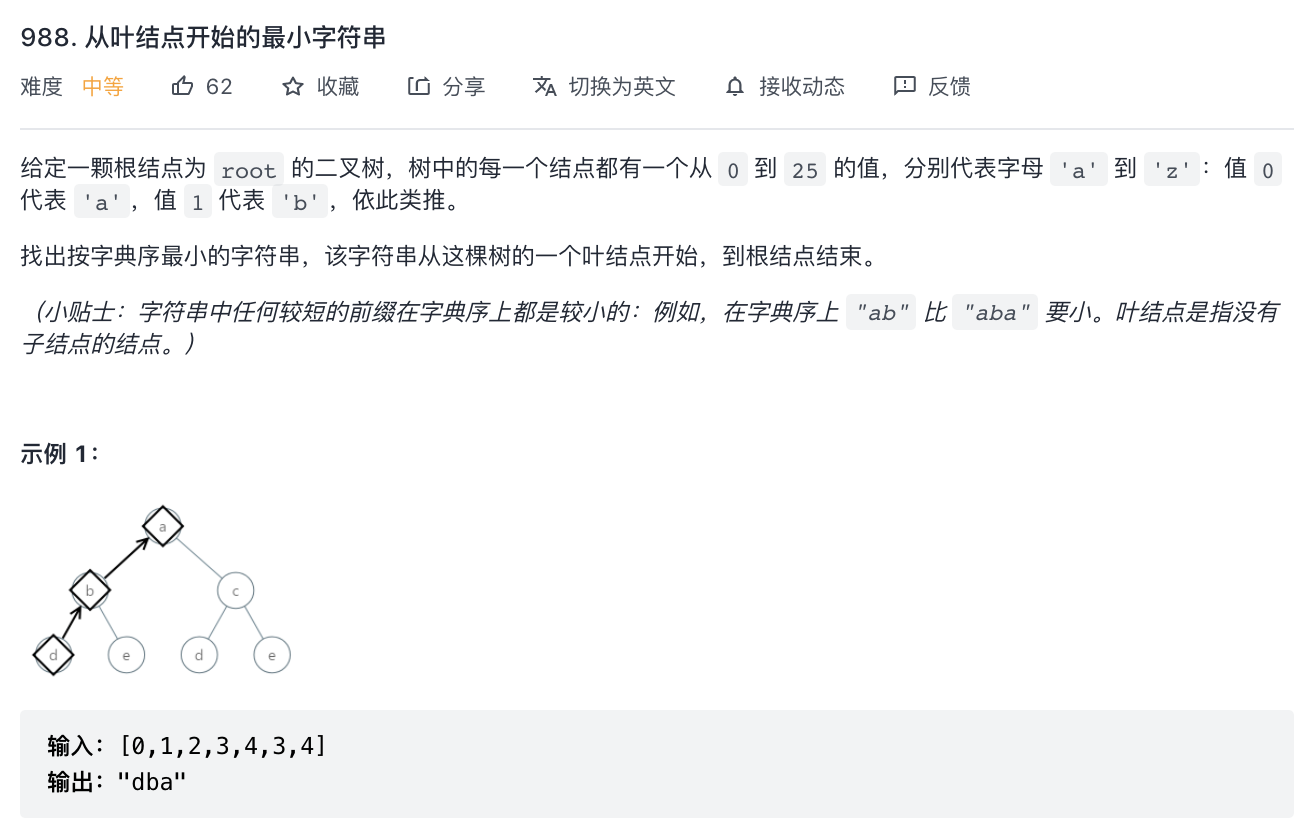
988-从叶节点开始的最小字符串

image.png
题意分析：

  • 从所有叶子节点到根节点的路径中，找到字符串值最小的字符串。

解题思路：

  • 类似 路径总和II 问题思路，找到所有路径，比较路径字符串大小。

注意点：
扩展：
代码：

  1.     String maxStr = "~";
  2.     public String smallestFromLeaf(TreeNode root) {
  3.         dfs(root, new StringBuilder());
  4.         return maxStr;
  5.     }
  7.     public void dfs(TreeNode root, StringBuilder path) {
  8.         if (root == null) {
  9.             return;
  10.         }
  12.         path.append((char)('a' + root.val));
  13.         if (root.left == null && root.right == null){
  14.                 path.reverse();
  15.                 String tmp = path.toString();
  16.                 path.reverse();
  17.                 if (tmp.compareTo(maxStr) < 0 ) {
  18.                     maxStr = tmp;
  19.                 }
  20.         }
  22.         dfs(root.left, path);
  23.         dfs(root.right, path);
  24.         // 回溯，删除 path 中最后一个节点，类似 路径总和II 问题思路
  25.         path.deleteCharAt(path.length() - 1);
  26.     }

前缀树

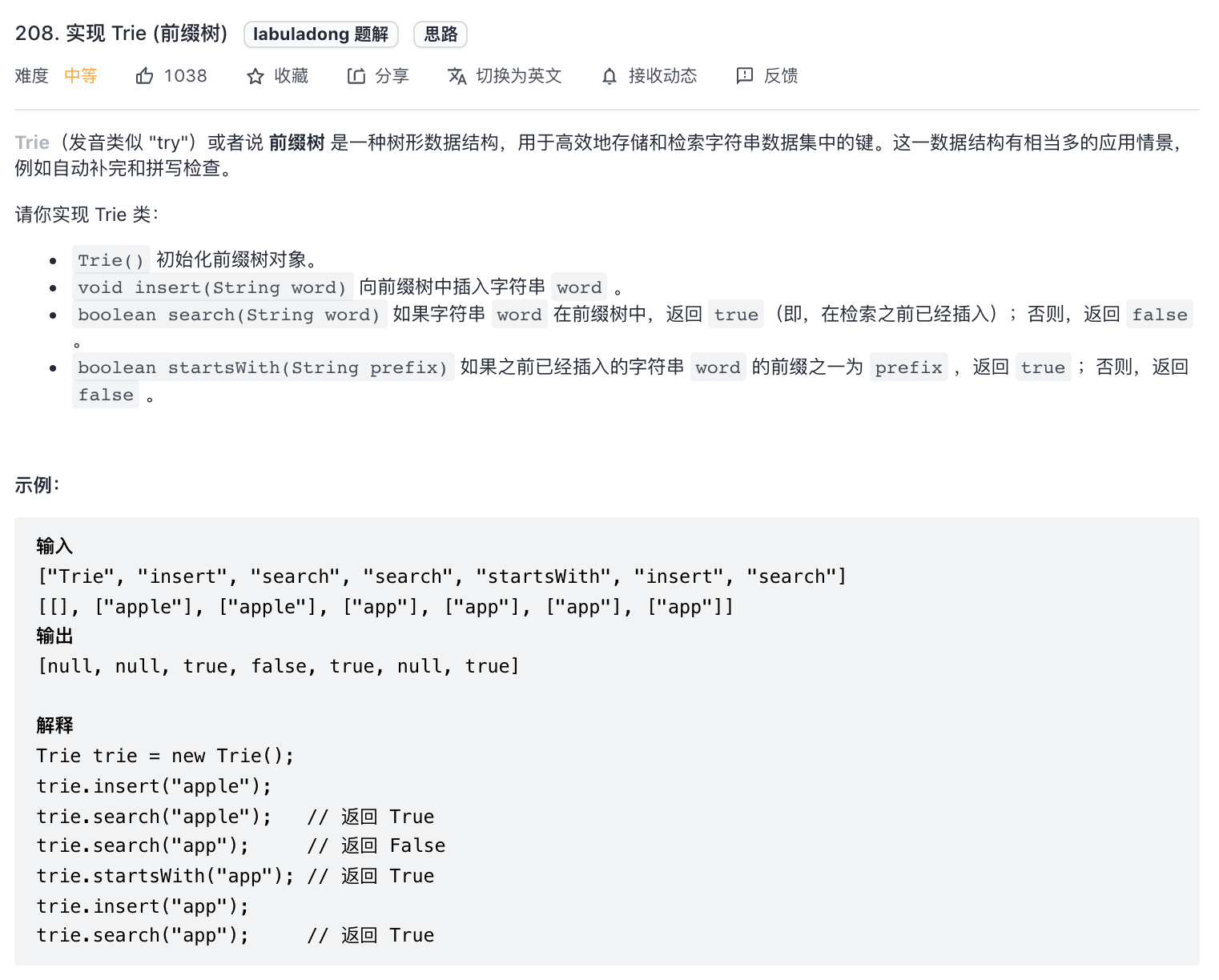
208-实现前缀树

image.png
题意分析：

  • 前缀树的新增、查找和前缀判断功能。

解题思路：

  • 定义前缀树，清楚前缀树的属性功能实现就相对容易。

注意点：

  • search() 方法实现的return逻辑，需要判断字符是否是前缀的特殊情况。

扩展：
代码：

  1. public class TreeTrieImpl_208 {
  3.   TrieNode root;
  5.   class TrieNode {
  6.     int pass;
  7.     int end;
  8.     TrieNode[] childs;
  10.     public TrieNode() {
  11.       pass = 0;
  12.       end = 0;
  13.       childs = new TrieNode[26];
  14.     }
  15.   }
  16.     public TreeTrieImpl_208() {
  17.     root = new TrieNode();
  18.     }
  20.     public void insert(String word) {
  21.     TrieNode node = root;
  22.     int idx;
  23.     char[] chs = word.toCharArray();
  24.     for (int i = 0; i < chs.length; i++) {
  25.         idx = chs[i] - 'a';
  26.         if (node.childs[idx] == null) {
  27.           node.childs[idx] = new TrieNode();
  28.         }
  29.         node.childs[idx].pass++;
  30.         node = node.childs[idx];
  31.     }
  32.     node.end++;
  33.     }
  35.     public boolean search(String word) {
  36.     TrieNode node = root;
  37.     int idx;
  38.     char[] chs = word.toCharArray();
  39.     for (int i = 0; i < chs.length; i++) {
  40.         idx = chs[i] - 'a';
  41.         if (node.childs[idx] == null) {
  42.             return false;
  43.         }
  44.         node = node.childs[idx];
  45.     }
  46.     // 不能直接返回ture，比如'apple'串中搜索'app'，要判断是否结束字符
  47.     return node.end != 0;
  48.     }
  50.     public boolean startsWith(String prefix) {
  51.       TrieNode node = root;
  52.       int idx;
  53.       char[] chs = prefix.toCharArray();
  54.       for (int i = 0; i < chs.length; i++) {
  55.           idx = chs[i] - 'a';
  56.           if (node.childs[idx] == null) {
  57.               return false;
  58.           }
  59.           node = node.childs[idx];
  60.       }
  61.     return true;
  62.     }
  64.     public static void main(String[] args) {
  65.         TreeTrieImpl_208 treeTrieImpl208 = new TreeTrieImpl_208();
  66.         treeTrieImpl208.insert("apple");
  67.         System.out.println(treeTrieImpl208.search("apple"));   // 返回 True
  68.         System.out.println(treeTrieImpl208.search("app"));     // 返回 False
  69.         System.out.println(treeTrieImpl208.startsWith("app")); // 返回 True
  70.         treeTrieImpl208.insert("app");
  71.         System.out.println(treeTrieImpl208.search("app"));     // 返回 True
  73.     }
  74. }

648-单词替换

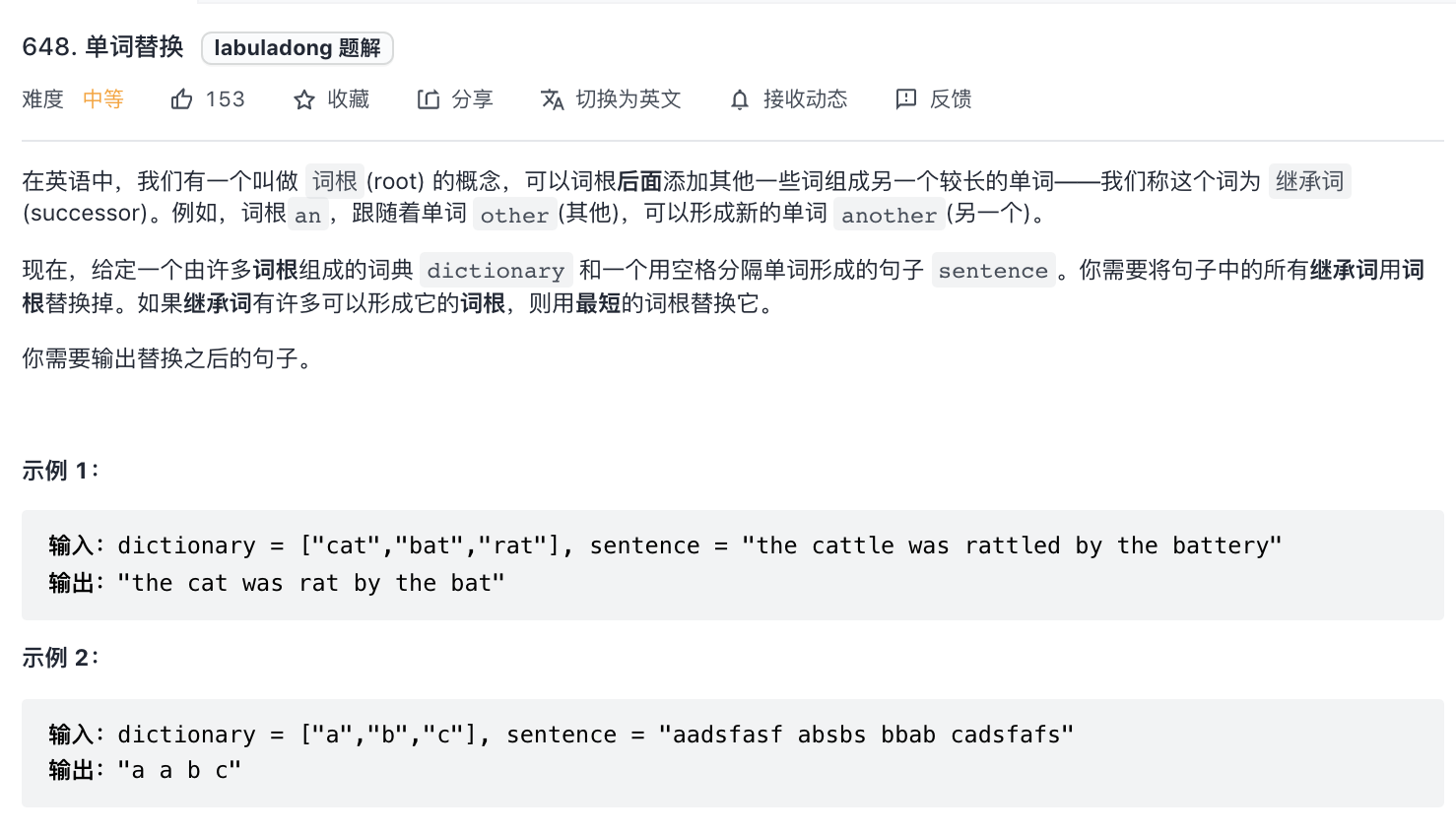
image.png
题意分析：

  • 如果一个单词在前缀词字典中存在前缀词，则用前缀词替换。

解题思路：

  • 选择字典还是句子作为前缀树是关键，然后判断前缀是否存在。

注意点：
扩展：
代码：

  1. public class WordReplace_648 {
  3.   TrieNode root = new TrieNode();
  5.     public void insert(String word) {
  6.         TrieNode node = root;
  7.         int idx;
  8.         char[] chs = word.toCharArray();
  9.         for (int i = 0; i < chs.length; i++) {
  10.             idx = chs[i] - 'a';
  11.             if (node.childs[idx] == null) {
  12.                 node.childs[idx] = new TrieNode();
  13.             }
  14.             node.pass++;
  15.             node = node.childs[idx];
  16.         }
  17.         node.end++;
  18.     }
  20.     public String shortestPrefix(String word) {
  21.         TrieNode node = root;
  22.         int idx;
  23.         char[] chs = word.toCharArray();
  24.         StringBuilder sb = new StringBuilder();
  25.         for (int i = 0; i < chs.length; i++) {
  26.             if (node.end != 0) {  // 找到了存在的前缀
  27.                 break;
  28.             }
  29.             idx = chs[i] - 'a';
  30.             if (node.childs[idx] == null) {
  31.                 return "";
  32.             }
  33.             sb.append(chs[i]);
  34.             node = node.childs[idx];
  35.         }
  36.       return sb.toString();
  37.     }
  39.     public String replaceWords(List<String> dictionary, String sentence) {
  40.         String[] strs = sentence.split(" ");
  41.         // 将 dictionary 中单词构建成前缀树
  42.         for (int i = 0; i < dictionary.size(); i++) {
  43.             insert(dictionary.get(i));
  44.         }
  45.         StringBuilder sb = new StringBuilder();
  46.         for (int i = 0; i < strs.length; i++) {
  47.             String prefix = shortestPrefix(strs[i]);
  48.             if (!prefix.isEmpty()) {
  49.                 sb.append(prefix);
  50.             } else {
  51.                 sb.append(strs[i]);
  52.             }
  53.             if (i != strs.length -1) {
  54.                 sb.append(" ");
  55.             }
  56.         }
  57.         return sb.toString();
  58.     }
  61.     public static void main(String[] args) {
  62.      WordReplace_648 obj = new WordReplace_648();
  63.      List<String> dictionary = new ArrayList<>(Arrays.asList("cat","bat","rat"));
  64.      String sentence = "the cattle was rattled by the battery";
  65.      System.out.println(obj.replaceWords(dictionary, sentence));
  66.     }
  67. }

211-添加与搜索

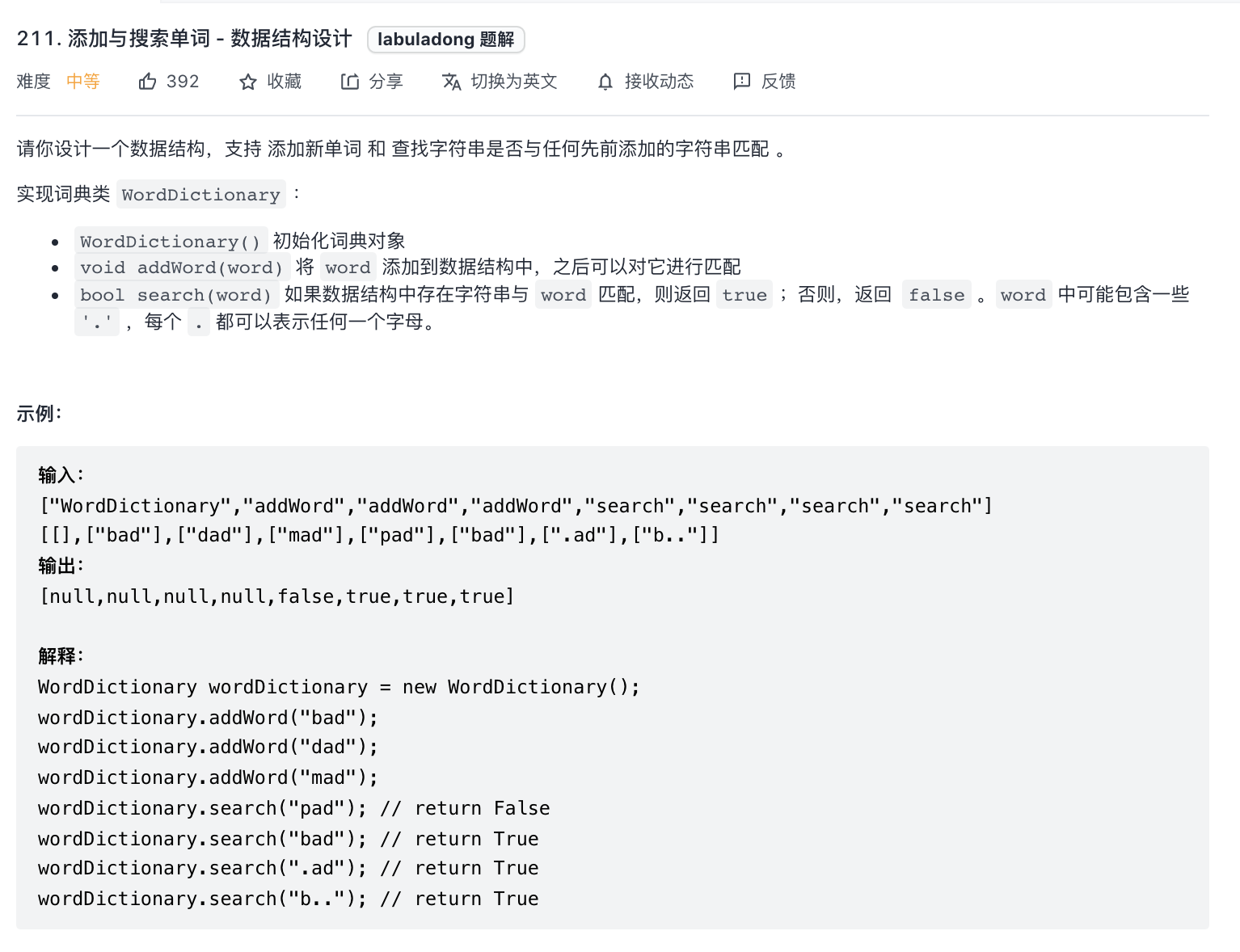
image.png
题意分析：

  • 前缀树的应用，向前缀树中添加字符串，然后查询prefix前缀是否存在，也存在模式匹配的前缀。

解题思路：

  • 构建前缀树，然后采用 dfs + 回溯 方式遍历。

注意点：

  • dfs 遍历添加参数 pattern 和 idx 表示递归体在向前遍历。这种递归走向还不是特别容易理解。

扩展：
代码：

  1. public class WordDictionary {
  3.   TrieNode root;
  5.     public WordDictionary() {
  6.     root = new TrieNode();
  7.     }
  9.     public void addWord(String word) {
  10.         if (word == null) {
  11.             return;
  12.         }
  13.         char[] chs = word.toCharArray();
  14.         TrieNode node = root;
  15.         node.pass++;
  16.         int idx;
  17.         // 遍历每一个字符，两种选择：有路径或者没有路径
  18.         for (int i = 0; i < chs.length; i++) {
  19.             idx = chs[i] - 'a';
  20.             if (node.childs[idx] == null) {
  21.                 // 没有路径则新建路径
  22.                 node.childs[idx] = new TrieNode();
  23.             }
  24.             node = node.childs[idx];
  25.             node.pass++;
  26.         }
  27.         node.end++;
  28.     }
  30.     public boolean search(String word) {
  31.     return hasKeyWithPattern(root, word, 0);
  32.     }
  35.     private boolean hasKeyWithPattern(TrieNode node, String pattern, int idx) {
  36.         if (node == null) {
  37.             return false;
  38.         }
  39.         if (idx == pattern.length()) {
  40.             return node.end != 0;
  41.         }
  42.         char ch = pattern.charAt(idx);
  43.         if (ch == '.') {
  44.             // '.' 符号则遍历所有子树
  45.             for (int i = 0; i < node.childs.length; i++) {
  46.                 if (node.childs[i] != null) {
  47.                     if (hasKeyWithPattern(node.childs[i], pattern, idx + 1))
  48.                       return true;
  49.                 }
  50.             }
  51.         } else {
  52.             return hasKeyWithPattern(node.childs[ch - 'a'], pattern, idx + 1);
  53.         }
  54.         return false;
  55.     }
  57.     public static void main(String[] args) {
  58.         WordDictionary wordDictionary = new WordDictionary();
  59.         wordDictionary.addWord("at");
  60.         wordDictionary.addWord("and");
  61.         wordDictionary.addWord("an");
  62.         wordDictionary.addWord("add");
  63.         System.out.println(wordDictionary.search("a")); // return False
  64.         System.out.println(wordDictionary.search(".at")); // return False
  65.         wordDictionary.addWord("bat");
  66.         System.out.println(wordDictionary.search(".at")); // return true
  68.     }
  69. }

677-键值映射

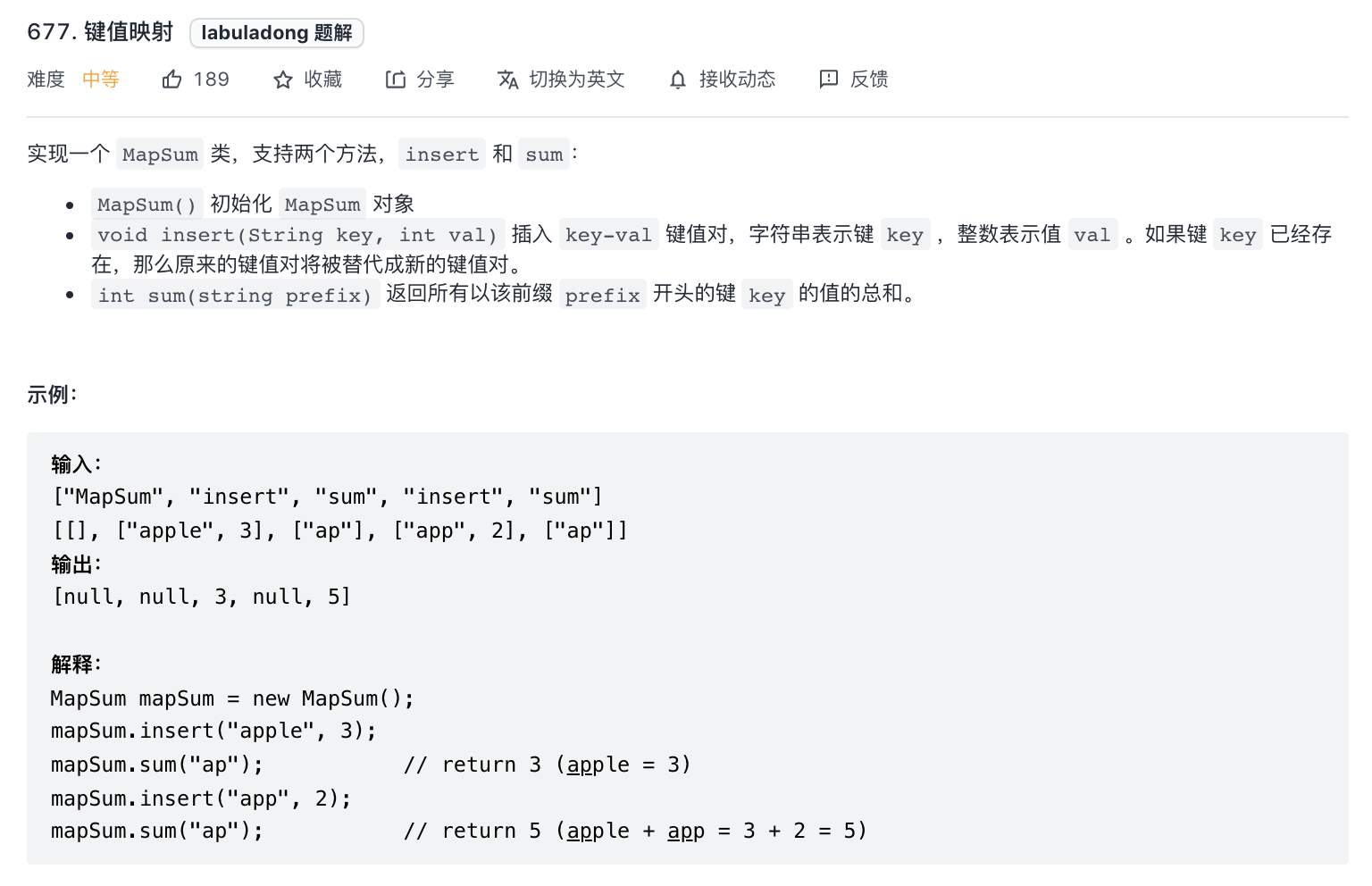
image.png
题意分析：

  • 首先是判断前缀prefix是否是存在字符串的前缀，如果是，求所有以 prefix 为前缀的字符的 val 的和。

解题思路：

  • 熟悉前缀树的基本操作就比较容易，首先构建前缀树，然后判断前缀 prefix 是否是合法的（即 getNode 判断前缀是否存在对应的路径节点），最后从 prefix 的路径结束节点开始 dfs 遍历，求所有叶子节点的 val 和。

注意点：
扩展：
代码：

  1. public class TrieMapSum_677 {
  2.     TrieNode root;
  4.     public TrieMapSum_677() {
  5.     root = new TrieNode();
  6.     }
  8.     public void insert(String key, int val) {
  9.     TrieNode node = root;
  10.     node.pass++;
  11.     int idx;
  12.     char[] chs = key.toCharArray();
  13.     for (int i = 0; i < chs.length; i++) {
  14.         idx = chs[i] - 'a';
  15.         if (node.childs[idx] == null) {
  16.             node.childs[idx] = new TrieNode();
  17.         }
  18.         node = node.childs[idx];
  19.         node.pass++;
  20.     }
  21.     node.end++;
  22.     node.val = val;
  23.     }
  26.     int sum = 0;
  28.     public int sum(String prefix) {
  29.       sum = 0;
  30.       TrieNode node = getNode(prefix);
  31.       if (node == null) {
  32.           return 0;
  33.       }
  34.       // 以node为根节点递归遍历，求其子树下所有叶子节点的和
  35.       dfs(node);
  36.     return sum;
  37.     }
  39.     public void dfs(TrieNode node) {
  40.       if (node == null) {
  41.           return;
  42.       }
  43.       if (node.end != 0) {
  44.           sum += node.val;
  45.       }
  46.       // 树的先序遍历。（多叉树）
  47.       for (int i = 0; i < node.childs.length; i++) {
  48.           if (node.childs[i] != null) {
  49.               dfs(node.childs[i]);
  50.           }
  51.       }
  52.     }
  54.     public TrieNode getNode(String prefix) {
  55.       TrieNode node = root;
  56.       int idx;
  57.     char[] chs = prefix.toCharArray();
  58.     for (int i = 0; i < chs.length; i++) {
  59.         idx = chs[i] - 'a';
  60.         if (node.childs[idx] == null) {
  61.             return null;
  62.         }
  63.         node = node.childs[idx];
  64.     }
  65.       return node;
  66.     }
  68.     public static void main(String[] args) {
  69.         TrieMapSum_677 mapSum = new TrieMapSum_677();
  70.         mapSum.insert("apple", 3);
  71.         System.out.println(mapSum.sum("ap"));           // return 3 (apple = 3)
  72.         mapSum.insert("app", 2);
  73.         System.out.println(mapSum.sum("ap"));           // return 5 (apple + app = 3 + 2 = 5)
  74.     }
  75. }

未分类

543-二叉树的直径

image.png
题意分析：

  • 直径定义：无非就是判断根节点的左右子树深度，两者和即为直径。

解题思路：

  • 后序遍历，计算每个节点的左右子树深度。

注意点：
扩展：
代码：

  1.     int res = 0;
  2.     public int diameterOfBinaryTree(TreeNode root) {
  3.         diameter(root);
  4.         return res;
  5.     }
  7.     public int diameter(TreeNode root) {
  8.         if (root == null) {
  9.             return 0;
  10.         }
  11.         int left = diameter(root.left);
  12.         int right = diameter(root.right);
  13.         if (root.left != null) {
  14.             left++;
  15.         } else {
  16.             left = 0;
  17.         }
  18.         if (root.right != null) {
  19.             right++;
  20.         } else {
  21.             right = 0;
  22.         }
  24.         System.out.println(root.val + ": left = " + left +"; right = " + right);
  26.         // 统计最长路径。如果是统计节点： left + right + 1
  27.         res = Math.max(res, left + right);
  28.         return Math.max(left, right);
  29.     }

101-对称二叉树

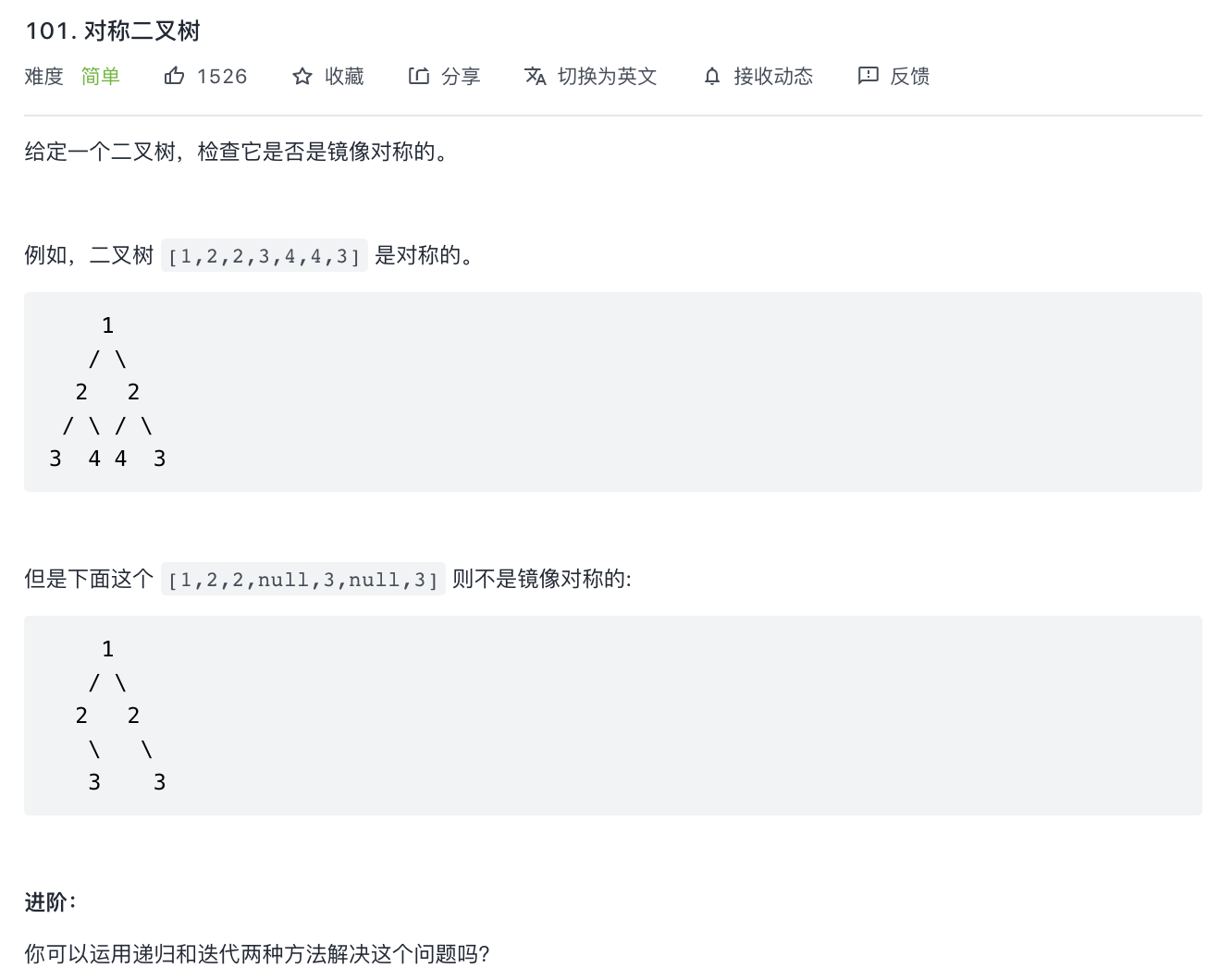
image.png
题意分析：

  • 判断 p.left 和 q.right 元素是否是一致的

解题思路：

  • bfs 遍历。每次入队两个元素，即对称的两个节点元素，判断是否对称。
  • dfs 遍历。递归判断两个节点。

注意点：
扩展：
代码：

  1.     /**
  2.      * bfs 遍历
  3.      * @param root
  4.      * @return
  5.      */
  6.     public boolean isSymmetric(TreeNode root) {
  7.         Queue<TreeNode> queue = new LinkedList<>();
  8.         queue.offer(root);
  9.         queue.offer(root);
  10.         while (!queue.isEmpty()) {
  11.             TreeNode p = queue.poll();
  12.             TreeNode q = queue.poll();
  14.             if (p == null && q == null) {
  15.                 continue;
  16.             }
  18.             if (p == null || q == null || p.val != q.val) {
  19.                 return false;
  20.             }
  22.             queue.offer(p.left);
  23.             queue.offer(q.right);
  25.             queue.offer(p.right);
  26.             queue.offer(q.left);
  27.         }
  28.         return true;
  29.     }
  31.     /**
  32.      * dfs 遍历
  33.      * @param root
  34.      * @return
  35.      */
  36.     public boolean isSymmetric2(TreeNode root) {
  37.         return check(root, root);
  38.     }
  40.     private boolean check(TreeNode p, TreeNode q) {
  41.         if (p == null && q == null) {
  42.             return true;
  43.         }
  44.         if (p == null || q == null)
  45.             return false;
  46.         return (p.val == q.val) && check(p.left, q.right) && check(p.right, q.left);
  47.     }

104-二叉树的最大深度

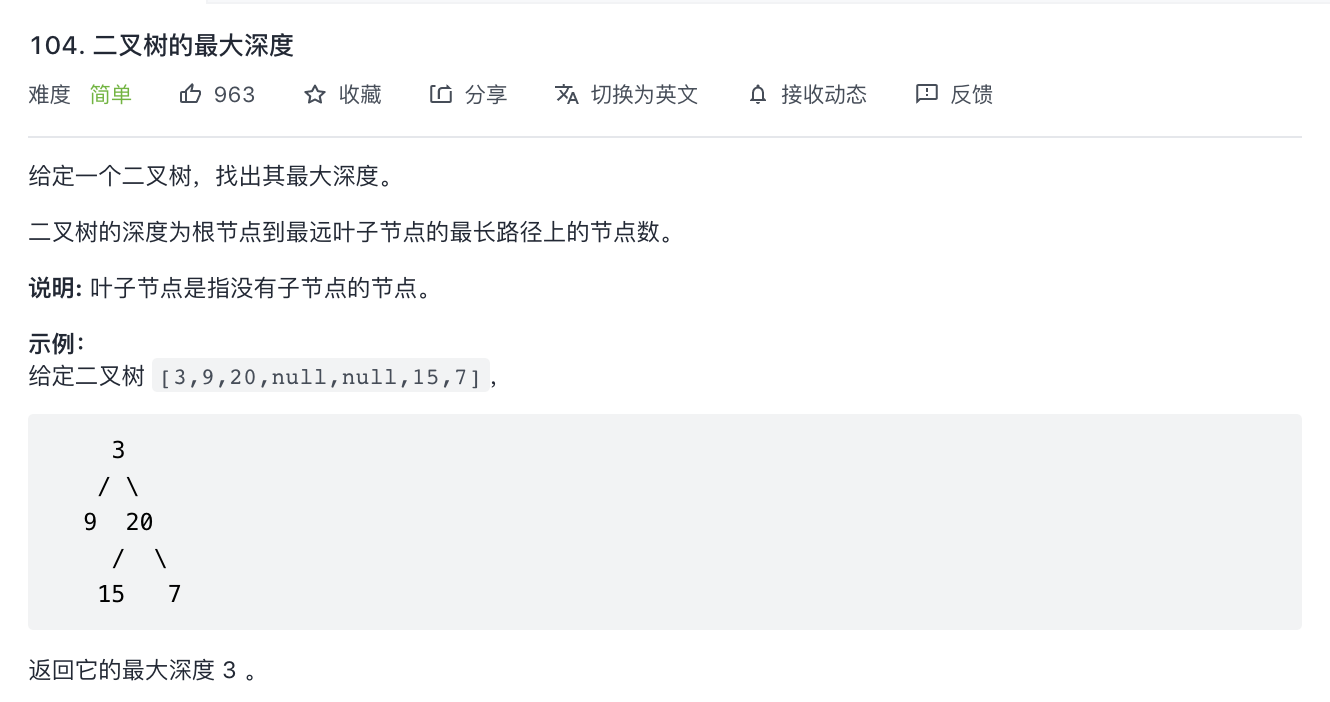
image.png
题意分析：

  • 树的最大深度。

解题思路：

  • bfs 最直观，遍历每一层的节点。
  • dfs 后序（自底向上）遍历记录每个节点的左右最大深度。

注意点：
扩展：
代码：

  1.     /**
  2.      * 树的深度优先遍历
  3.      * @param root
  4.      * @return
  5.      */
  6.     public int maxDepth(TreeNode root) {
  7.         if (root == null) {
  8.             return 0;
  9.         }
  10.         int leftDepth = maxDepth(root.left);
  11.         int rightDepth = maxDepth(root.right);
  12.         return Math.max(leftDepth, rightDepth) + 1;
  13.     }
  15.     public int maxDepth2(TreeNode root) {
  16.         if (root == null) {
  17.             return 0;
  18.         }
  19.         Queue<TreeNode> queue = new LinkedList<>();
  20.         queue.offer(root);
  21.         int depth = 0;
  22.         while (!queue.isEmpty()) {
  23.             // size 记录每一层节点的数量，一层节点出队列完毕后深度+1
  24.             int size = queue.size();
  25.             while (size > 0 ) {
  26.                 TreeNode node = queue.poll();
  27.                 if (node.left != null) {
  28.                     queue.offer(node.left);
  29.                 }
  30.                 if (node.right != null) {
  31.                     queue.offer(node.right);
  32.                 }
  33.                 size--;
  34.             }
  35.             depth++;
  36.         }
  37.         return depth;
  38.     }

111-二叉树的最小深度

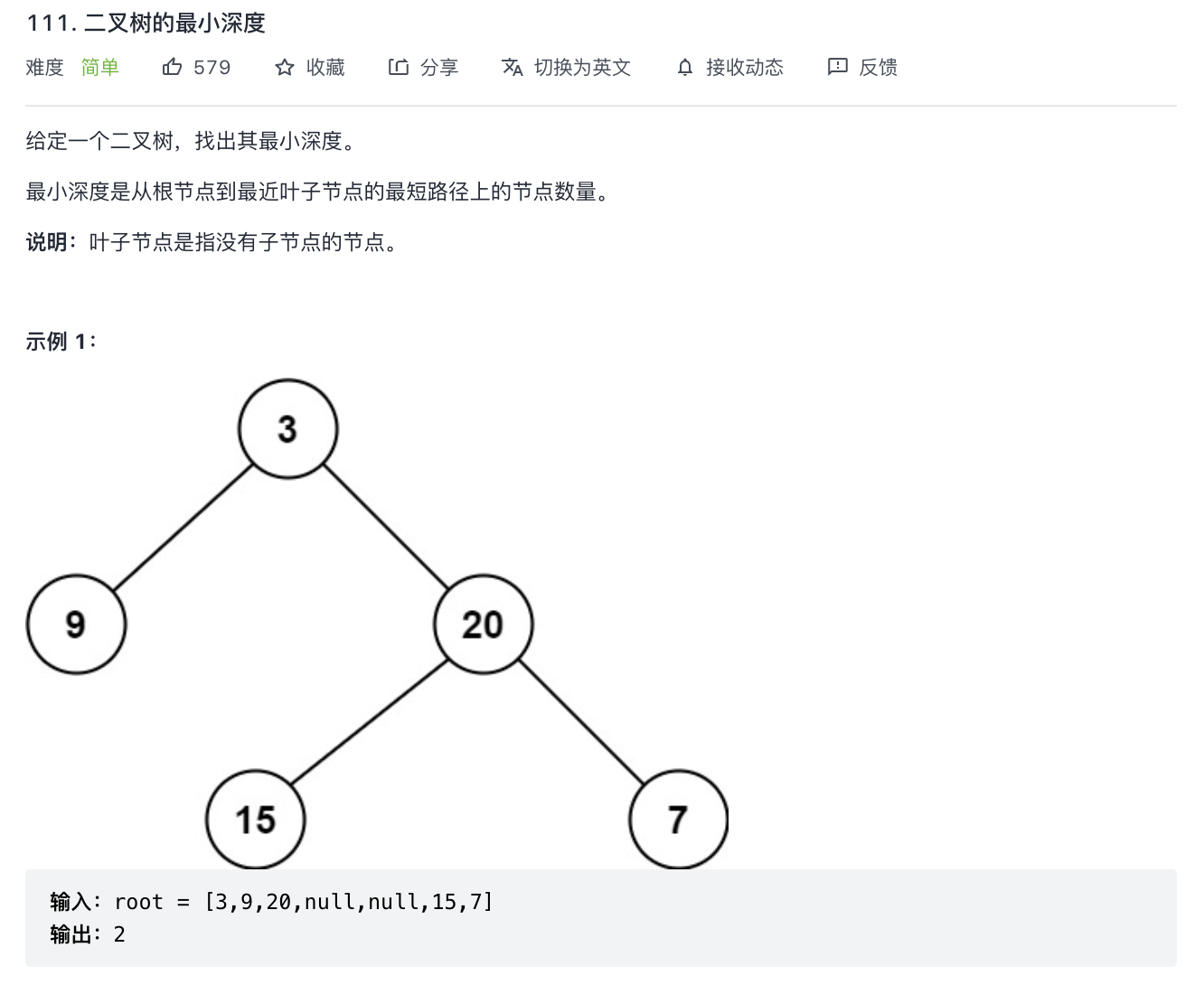
image.png
题意分析：

  • 和最大深度差不多。

解题思路：

  • bfs 遍历最简单，遇到叶子节点直接返回深度。

注意点：
扩展：
代码：

  1.     int res = Integer.MAX_VALUE;
  2.     public int minDepth(TreeNode root) {
  3.         if (root == null) {
  4.             return 0;
  5.         }
  6.         Queue<TreeNode> queue = new LinkedList<>();
  7.         queue.offer(root);
  8.         int depth = 0;
  9.         while (!queue.isEmpty()) {
  10.             // size 记录每一层节点的数量，一层节点出队列完毕后深度+1
  11.             int size = queue.size();
  12.             while (size > 0 ) {
  13.                 TreeNode node = queue.poll();
  14.                 if (node.left == null && node.right == null) {
  15.                     return ++depth;
  16.                 }
  17.                 if (node.left != null) {
  18.                     queue.offer(node.left);
  19.                 }
  20.                 if (node.right != null) {
  21.                     queue.offer(node.right);
  22.                 }
  23.                 size--;
  24.             }
  25.             depth++;
  26.         }
  27.         return depth;
  28.     }

987-二叉树的垂序遍历

image.png
题意分析：

  • 根据每个节点 x/y 值对树节点进行遍历。

解题思路：

  • 逻辑思路比较清晰。
    • 先遍历树，计算每个节点的 x 和 y 值。
    • 然后对所有节点排序，自定义排序器，分别按 y、x、val 升序遍历。
    • 分组输出节点元素。

注意点：
扩展：
代码：

  1. /**
  2.  * 题目考查的知识点：
  3.  * 1、二叉树的遍历；
  4.  * 2、Java 比较器的实现；
  5.  * 3、数组/List 的遍历技巧。
  6.  *  List[1,2,3,3,3,4,4,5] = 统计每个单词出现的次数，并放在不同集合中。[[1],[2],[3,3,3],[4,4],[5]]
  7.  */
  8. public class VerticalTraversal_987 {
  10.     List<VerticalNode> nodeList = new ArrayList<>();
  12.     public List<List<Integer>> verticalTraversal(TreeNode root) {
  13.         // 遍历树节点，获得每个节点的 [x, y , val] 组值
  14.         dfs(root, 0, 0);
  16. //        System.out.println("----------排序前--------");
  17. //        for (VerticalNode node : nodeList) {
  18. //            System.out.println(node.val + ": " + node.x + ": " + node.y);
  19. //        }
  21.         // 排序，先根据列 y 升序排序，如果 y 相同，则按照 val 升序排序
  22.         Collections.sort(nodeList, new Comparator<VerticalNode>() {
  23.             @Override
  24.             public int compare(VerticalNode o1, VerticalNode o2) {
  25.                 if (o1.y != o2.y) {
  26.                     return o1.y - o2.y;   // 按 y 升序
  27.                 } else if (o1.x != o2.x) {
  28.                     return o1.x - o2.x; // 按 x 升序
  29.                 } else {
  30.                     return o1.val - o2.val;
  31.                 }
  32.             }
  33.         });
  35.         System.out.println("----------排序后--------");
  36.         for (VerticalNode node : nodeList) {
  37.             System.out.println(node.val + ": " + node.x + ": " + node.y);
  38.         }
  40.         // 排序后输出结果
  41.         List<List<Integer>> retList = new ArrayList<>();
  42.         List<Integer> list = new ArrayList<>();
  44.         int last_y = Integer.MIN_VALUE;
  45.         // 记录有多少组不同 y 元素
  46.         int size = -1;
  48.         // 此时遍历可忽略 行x 的影响，因为 x 是有序的，List 也是有序的，根据 y 遍历输出 val 的值即可。
  49.         for (VerticalNode node : nodeList) {
  50.             if (node.y != last_y) {
  51.               size++;
  52.                 last_y = node.y;
  53.                 list.add(node.val);
  54.                 retList.add(list);
  55.                 list = new ArrayList<>();
  56.             } else {
  57.                 retList.get(size).add(node.val);
  58.             }
  59.         }
  60.         System.out.println(retList);
  62.         return retList;
  63.     }
  65.     public void dfs(TreeNode root, int x, int y) {
  66.         if (root == null) {
  67.             return;
  68.         }
  69.         nodeList.add(new VerticalNode(root.val, x, y));
  70.         // 对左右子树递归遍历
  71.         dfs(root.left, x+1, y-1);
  72.         dfs(root.right, x+1, y+1);
  73.     }
  75.     /**
  76.      *       1
  77.      *   2      3
  78.      *        4     5
  79.      */
  80.     public static void main(String[] args) {
  81.         VerticalTraversal_987 obj = new VerticalTraversal_987();
  82.         System.out.println(obj.verticalTraversal(Utils.createTree2()));
  83.     }
  85.     class VerticalNode {
  86.         int val;
  87.         int x;
  88.         int y;
  90.         public VerticalNode(int val, int x, int y) {
  91.             this.val = val;
  92.             this.x = x;
  93.             this.y = y;
  94.         }
  95.     }
  96. }

模版

题意分析：
解题思路：
注意点：
扩展：
代码：