子序列问题

子序列问题分类：

  • 只涉及一个子串。
    • 当前状态只和上一个状态有关，即 dp[i] 只和 dp[i-1] 状态有关。（53题）
    • 当前状态和前面所有状态有关，即 dp[i] 和 dp[0-(i-1)] 状态有关。（300题）

  • 涉及两个字串。

    53-最大子序列

    image.png
    题意分析：

  • 判断子数组连续元素和最大。

解题思路：

  • 动态规划。dp[i] 状态的结果一定是以 nums[i] 为结束元素的值。

注意点：
拓展：

  • 如何输出和最大的连续子数组？

代码：

  1.     public int maxSubArray(int[] nums) {
  2.         int n = nums.length;
  4.         // 状态数组。nums[1...i] 以 nums[i] 结尾的子数组的最大和
  5.         int[] dp = new int[n];
  7.         // base case
  8.         dp[0] = nums[0];
  10.         // 状态转换
  11.         for (int i = 1; i < n; i++) {
  12.             dp[i] = Math.max(nums[i], dp[i-1] + nums[i]);
  13.         }
  15.         // 求解
  16.         int max_sum = Integer.MIN_VALUE;
  17.         for (int i = 0; i < n; i++) {
  18.             if (dp[i] > max_sum) {
  19.                 max_sum = dp[i];
  20.             }
  21.         }
  22.         return max_sum;
  23.     }

300-最长递增子序列（动规/动规+二分/贪心+二分）

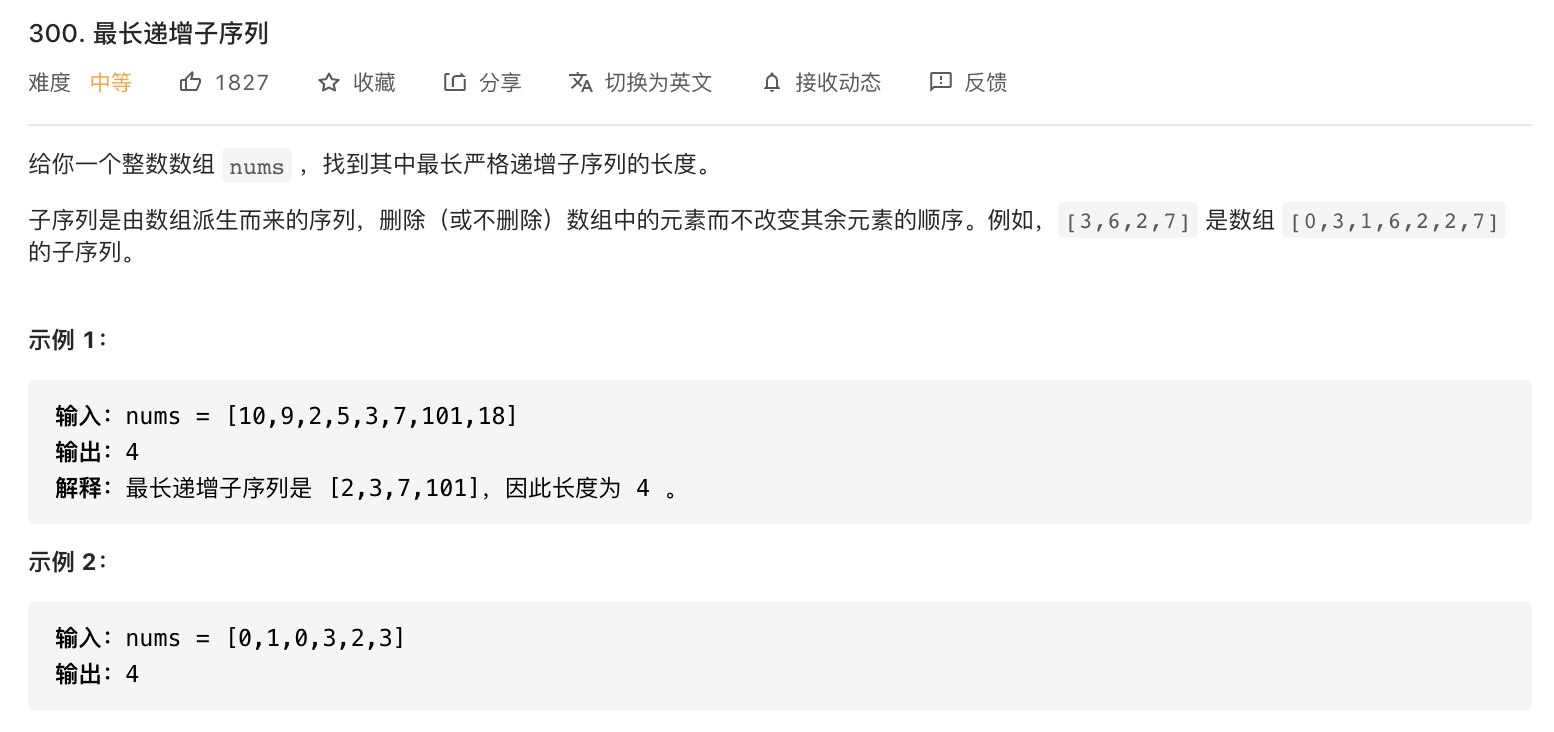
image.png
题意分析：

  • 从数组中找出最长递增的一串数字。

解题思路：

注意点：
拓展：

  • 如何输出最长递增子序列？

代码：

  1.     public int lengthOfLIS(int[] nums) {
  2.         int n = nums.length;
  4.         // 状态数组
  5.         int[] dp = new int[n];
  7.         // base case
  8.         Arrays.fill(dp, 1);
  10.         // 状态转换
  11.         for (int i = 0; i < n; i++) {
  12.             for (int j = 0; j < i; j++) {
  13.                 if (nums[i] > nums[j]) {
  14.                     // i 会不断更新，dp[i] 会存在覆盖的情况
  15.                     dp[i] = Math.max(dp[j] + 1, dp[i]);
  16.                 }
  17.             }
  18.         }
  20. //        System.out.println(Arrays.toString(dp));
  22.         // 求数组最大值等价于：ans = Arrays.stream(dp).max().getAsInt();
  23.         int ans = 0;
  24.         for (int i = 0; i < n; i++) {
  25.             ans = Math.max(ans, dp[i]);
  26.         }
  28.         return ans;
  29.     }

股票买卖问题

买卖股票问题（动规）

动态规划问题三部曲：

  1. 状态数组及状态转换（备忘录）（难点）。
  2. base case。就是刚开始时的特殊情况。
  3. 求解。

总体分为三类：

  1. 只允许交易一次。
  2. 允许交易无限次，含冷冻期，含手续费。
  3. 允许交易 k 次（最难）。

股票操作：买入、卖出、无操作。
股票状态：不持有、持有

状态数组定义：

  • 只有一次交易或者没有限制交易次数的状态数组：

dp[i][0/1]：第 i 天不持有/持有股票的最大利润。

  • 允许进行 k 次交易的状态数组：

dp[i][k][0/1]：第 i 天最多还能进行 k 次交易时不持有/持有股票的最大利润。

拓展：

  • 如何对状态数组进行状态压缩？

121-买卖股票的最佳时机

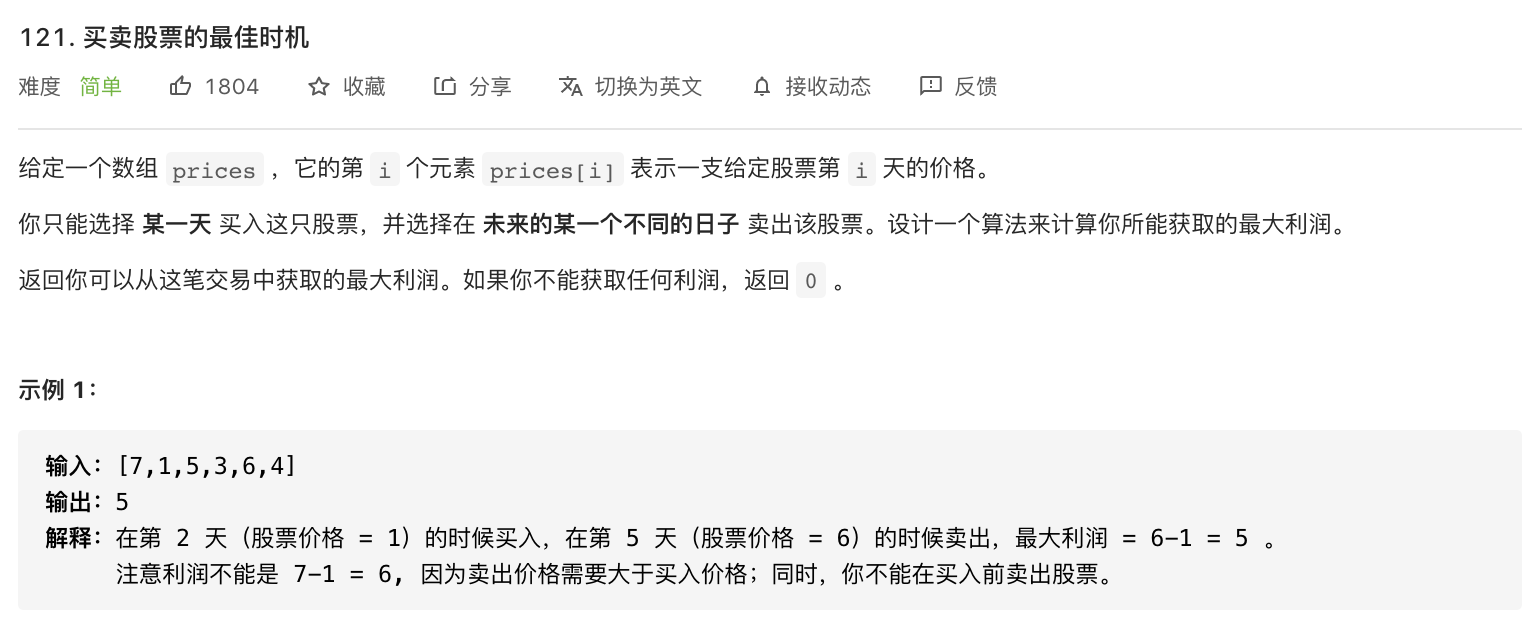
image.png
代码：

  1.     public int maxProfit(int[] prices) {
  2.         int len = prices.length;
  3.         if (len < 2) {
  4.             return 0;
  5.         }
  6.         int[][] dp = new int[len][2];
  8.         // base case
  9.         dp[0][0] = 0;
  10.         dp[0][1] = -prices[0];
  12.         //状态转换。只允许交易一次，说明只会有某一天持有
  13.         for(int i = 1; i < len; i++) {
  14.             dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] + prices[i]);
  15.             // 特殊情况，只进行一次交易，如果持有一定是当天买的。
  16.             dp[i][1] = Math.max(- prices[i], dp[i-1][1]);
  17. //            System.out.println(i + ": dp[i][0]=" + dp[i][0] + ";  dp[i][1]= " + dp[i][1]);
  18.         }
  20.         // 求解
  21.         return dp[len - 1][0];
  22.     }

122-买卖股票的最佳时机 II

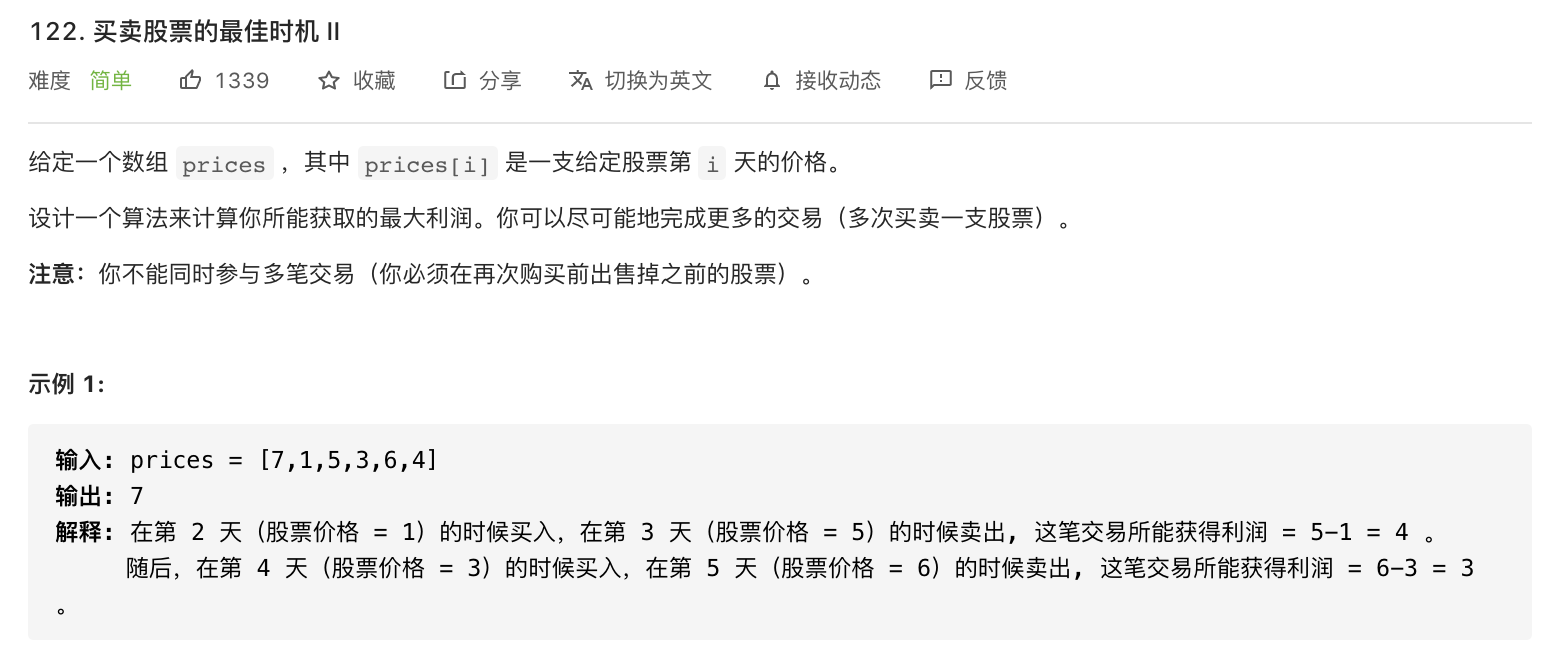
image.png
代码：

  1.     public int maxProfit(int[] prices) {
  2.         int len = prices.length;
  3.         if (len < 2) {
  4.             return 0;
  5.         }
  6.         int[][] dp = new int[len][2];
  8.         // base case
  9.         dp[0][0] = 0;
  10.         dp[0][1] = -prices[0];
  12.         // 状态转换。允许交易多次，说明持有天数没限制
  13.         for (int i = 1; i < len; i++) {
  14.             dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] + prices[i]);
  15.             dp[i][1] = Math.max(dp[i-1][0] - prices[i], dp[i-1][1]);
  16. //            System.out.println(i + ": dp[i][0]=" + dp[i][0] + ";  dp[i][1]= " + dp[i][1]);
  17.         }
  19.         // 求解
  20.         return dp[len-1][0];
  21.     }

123-买卖股票的最佳时机 III

image.png
代码：

  1.     public int maxProfit(int[] prices) {
  2.         int len = prices.length;
  3.         if (len < 2) {
  4.             return 0;
  5.         }
  6.         int max_k = 2;
  7.         int[][][] dp = new int[len][max_k+1][2];
  9.         // base case
  10.         // dp[i][0][0] = 0
  11.         for (int i = 0; i < len; i++) {
  12.             dp[i][0][0] = 0;
  13.         }
  14.         // dp[i][0][1] = Interger.minval
  15.         for (int i = 0; i < len; i++) {
  16.             dp[i][0][1] = Integer.MIN_VALUE;
  17.         }
  18.         // dp[0][k][0] = 0
  19.         for (int k = 0; k <= max_k; k++) {
  20.             dp[0][k][0] = 0;
  21.         }
  23.         // dp[0][k][1] = Integer.minval
  24. //        for (int k = 0; k <= max_k; k++) {
  25. //            dp[0][k][1] = prices[0];
  26. //        }
  27.         dp[0][0][1] = Integer.MIN_VALUE;
  28.         dp[0][1][1] = - prices[0];
  29.         dp[0][2][1] = - prices[0];
  31.         // dp 状态转换
  32.         for (int i = 1; i < len; i++) {
  33.             for (int k = 1; k <= max_k; k++) {
  34.                 // 第2种情况：前面最多交易 k 次，这次卖出（一次完整交易）不计入交易次数
  35.                 dp[i][k][0] = Math.max(dp[i-1][k][0], dp[i-1][k][1] + prices[i]);
  36.                 // 第2种情况：前面最多交易 k-1 次，加上这次买入
  37.                 dp[i][k][1] = Math.max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i]);
  38. //                System.out.println("i = " + i + "; k = " + k + ": dp[i][k][0]=" + dp[i][k][0] + ";  dp[i][k][1]= " + dp[i][k][1]);
  39.             }
  40.         }
  42.         // 求解。最后一天，最多交易 k 次后不持有股票的最大利润。
  43.         return dp[len-1][max_k][0];
  44.     }

188-买卖股票的最佳时机 IV

image.png
代码：

  1.     public int maxProfit(int k, int[] prices) {
  2.         int len = prices.length;
  3.         if (len < 2) {
  4.             return 0;
  5.         }
  6.         // 这里 k 其实是有上限交易次数的
  7.         int max_k = Math.min(k, len / 2);
  8.         int[][][] dp = new int[len][max_k+1][2];
  10.         // base case
  11.         // dp[i][0][0] = 0
  12.         for (int i = 0; i < len; i++) {
  13.             dp[i][0][0] = 0;
  14.         }
  15.         // dp[i][0][1] = Interger.minval
  16.         for (int i = 0; i < len; i++) {
  17.             dp[i][0][1] = Integer.MIN_VALUE;
  18.         }
  19.         // dp[0][k][0] = 0
  20.         for (int ki = 0; ki <= max_k; ki++) {
  21.             dp[0][ki][0] = 0;
  22.         }
  24.         dp[0][0][1] = Integer.MIN_VALUE;
  25.         for (int ki = 1; ki <= max_k; ki++)
  26.             dp[0][ki][1] = - prices[0];
  28.         // dp 状态转换
  29.         for (int i = 1; i < len; i++) {
  30.             for (int ki = 1; ki <= max_k; ki++) {
  31.                 dp[i][ki][0] = Math.max(dp[i-1][ki][0], dp[i-1][ki][1] + prices[i]);
  32.                 dp[i][ki][1] = Math.max(dp[i-1][ki][1], dp[i-1][ki-1][0] - prices[i]);
  33.                 System.out.println("i = " + i + "; ki = " + ki + ": dp[i][ki][0]=" + dp[i][ki][0] + ";  dp[i][ki][1]= " + dp[i][ki][1]);
  34.             }
  35.         }
  37.         // 求解
  38.         return dp[len-1][max_k][0];
  39.     }

309-最佳买卖股票时机含冷冻期

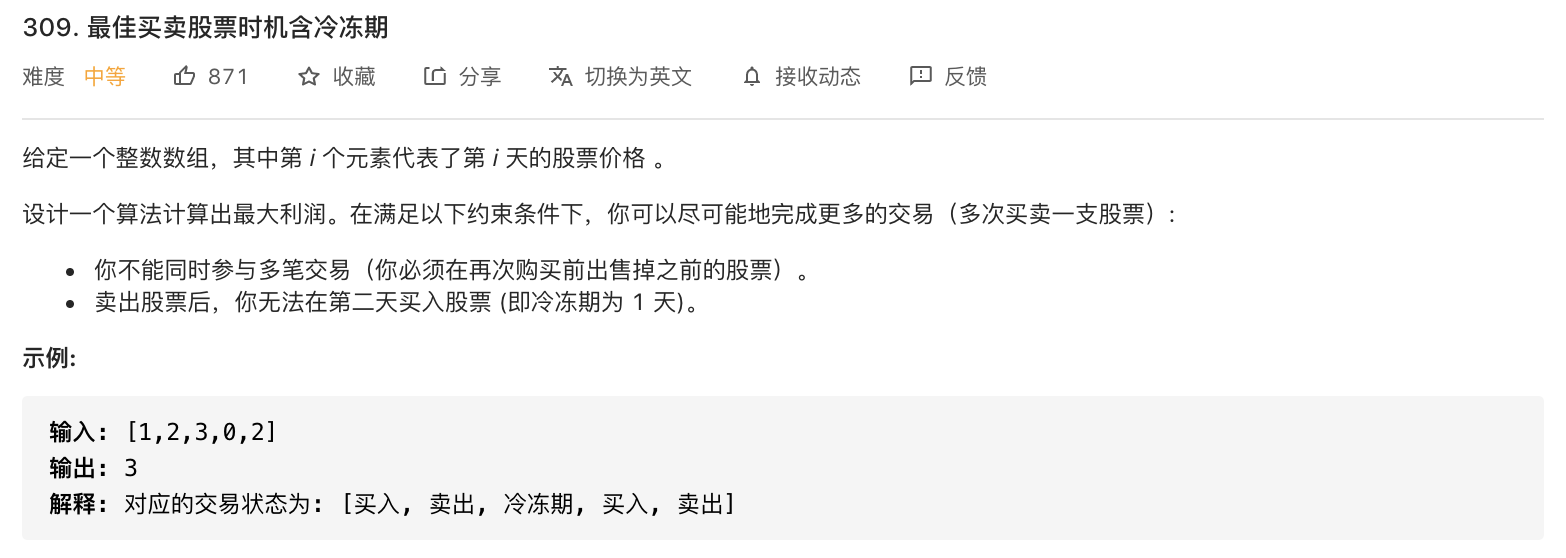
image.png
代码：

  1.     public int maxProfit(int[] prices) {
  2.         int len = prices.length;
  3.         if (len < 2) {
  4.             return 0;
  5.         }
  6.         int[][] dp = new int[len][2];
  8.         // base case
  9.         dp[0][0] = 0;
  10.         dp[0][1] = -prices[0];
  12.         // 状态转换
  13.         for (int i = 1; i < len; i++) {
  14.             dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] + prices[i]);
  15.             if (i == 1 ) {
  16.                 // base case. dp[-1][1] 下标不存在，i 天购买，利润为 -prices[i]
  17.                 dp[i][1] = Math.max(-prices[i], dp[i-1][1]);
  18.             } else {
  19.               // 当天进行交易的前一天冷冻
  20.                 dp[i][1] = Math.max(dp[i - 2][0] - prices[i], dp[i - 1][1]);
  21.             }
  22.             System.out.println(i + ": dp[i][0]=" + dp[i][0] + ";  dp[i][1]= " + dp[i][1]);
  23.         }
  25.         // 求解
  26.         return dp[len-1][0];
  27.     }

714-买卖股票的最佳时机含手续费

image.png
代码：

  1.     public int maxProfit(int[] prices, int fee) {
  2.         int len = prices.length;
  3.         if (len < 2) {
  4.             return 0;
  5.         }
  6.         int[][] dp = new int[len][2];
  8.         // base case
  9.         dp[0][0] = 0;
  10.         dp[0][1] = -prices[0] - fee;
  12.         // 状态转换
  13.         for (int i = 1; i < len; i++) {
  14.             dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] + prices[i]);
  15.             dp[i][1] = Math.max(dp[i-1][0] - prices[i] - fee, dp[i-1][1]);
  16. //            System.out.println(i + ": dp[i][0]=" + dp[i][0] + ";  dp[i][1]= " + dp[i][1]);
  17.         }
  19.         // 求解
  20.         return dp[len-1][0];
  21.     }

路径问题（动规）

62-不同路径

image.png
题意分析：

  • m*n 的矩阵中，从左上角走到右下角有多少种走法。

解题思路：

  • 动态规划。dp[i][j] 结果和 dp[i-1][j] / dp[i][j-1] 状态的关系。

注意点：
扩展：
代码：

  1.     /**
  2.     *   时间复杂度 O(m*n)
  3.     *   空间复杂读 O(m*n)
  4.      * 借助状态数组，增加空间复杂度。
  5.      *
  6.      * @param m
  7.      * @param n
  8.      * @return
  9.      */
  10.     public int uniquePaths(int m, int n) {
  11.       // 状态数组
  12.         int[][] dp = new int[m][n];
  14.         // base case
  15.         dp[0][0] = 0;
  16.         for (int i = 0; i < m; i++) {
  17.             dp[i][0] = 1;
  18.         }
  19.         for (int i = 0; i < n; i++) {
  20.             dp[0][i] = 1;
  21.         }
  22.         // 状态转移
  23.         for (int i = 1; i < m; i++) {
  24.             for (int j = 1; j < n; j++) {
  25.                 dp[i][j] = dp[i-1][j] + dp[i][j-1];
  26.                 System.out.println(i + "-" + j + ": dp[i][j] = " + dp[i][j]);
  27.             }
  28.         }
  29.         return dp[m-1][n-1];
  30.     }

63-不同路径 II

image.png
image.png
题意分析：

  • 加上不可达节点时的走法。

解题思路：

  • 动态规划。

注意点：

  • 初始化时要考虑障碍的初始值。

扩展：
代码：

  1.     public int uniquePathsWithObstacles(int[][] obstacleGrid) {
  2.         int m = obstacleGrid.length, n = obstacleGrid[0].length;
  3.         // 状态数组。（数组初始化时值都为0）
  4.         int[][] dp = new int[m][n];
  5.         for (int i = 0; i < m; i++) {
  6.             System.out.println(Arrays.toString(dp[i]));
  7.         }
  9.         // base case.
  10.         // 这里的 && 判断很特殊，如果不满足直接退出 for 循环。
  11.         // for 循环改成 while 逻辑就好理解，相当于 while 循环直接 break 了
  12.         for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) {
  13.             dp[i][0] = 1;
  14.         }
  15.         for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) {
  16.             dp[0][j] = 1;
  17.         }
  19.         // 状态转移
  20.         for (int i = 1; i < m; i++) {
  21.             for (int j = 1; j < n; j++) {
  22.                 if (obstacleGrid[i][j] == 0)
  23.                     dp[i][j] = dp[i-1][j] + dp[i][j-1];
  24. //                System.out.println(i + "-" + j + ": dp[i][j] = " + dp[i][j]);
  25.             }
  26.         }
  28.         // 求解
  29.         return dp[m-1][n-1];
  30.     }

64-最小路径和

image.png
题意分析：

  • 无非就是把不同路径改成计算路径上节点的和，本质一样。

解题思路：

  • 动态规划。

注意点：

  • 和“不同路径”有点不一样，“不同路径”问题第一行/列的 base case 都是 1，base case 初始化时时要计算节点值的。

扩展：
代码：

  1.     public int minPathSum(int[][] grid) {
  2.         int m = grid.length, n = grid[0].length;
  4.         // 状态数组
  5.         int[][] dp = new int[m][n];
  7.         // base case，初始化时是要计算值的。
  8.         dp[0][0] = grid[0][0];
  9.         for (int i = 1; i < m; i++) {
  10.             dp[i][0] = dp[i-1][0] + grid[i][0];
  11.         }
  12.         for (int j = 1; j < n; j++) {
  13.             dp[0][j] = dp[0][j-1] + grid[0][j];
  14.         }
  16.         // 状态转换
  17.         for (int i = 1; i < m; i++) {
  18.             for (int j = 1; j < n; j++) {
  19.                 // 注意这里 +grid[i][j] 的值是都要加上的
  20.                 dp[i][j] = Math.min(dp[i-1][j], dp[i][j-1]) + grid[i][j];
  21.             }
  22.         }
  24.         // 求解
  25.         return dp[m-1][n-1];
  26.     }

贪心问题

55-跳跃游戏

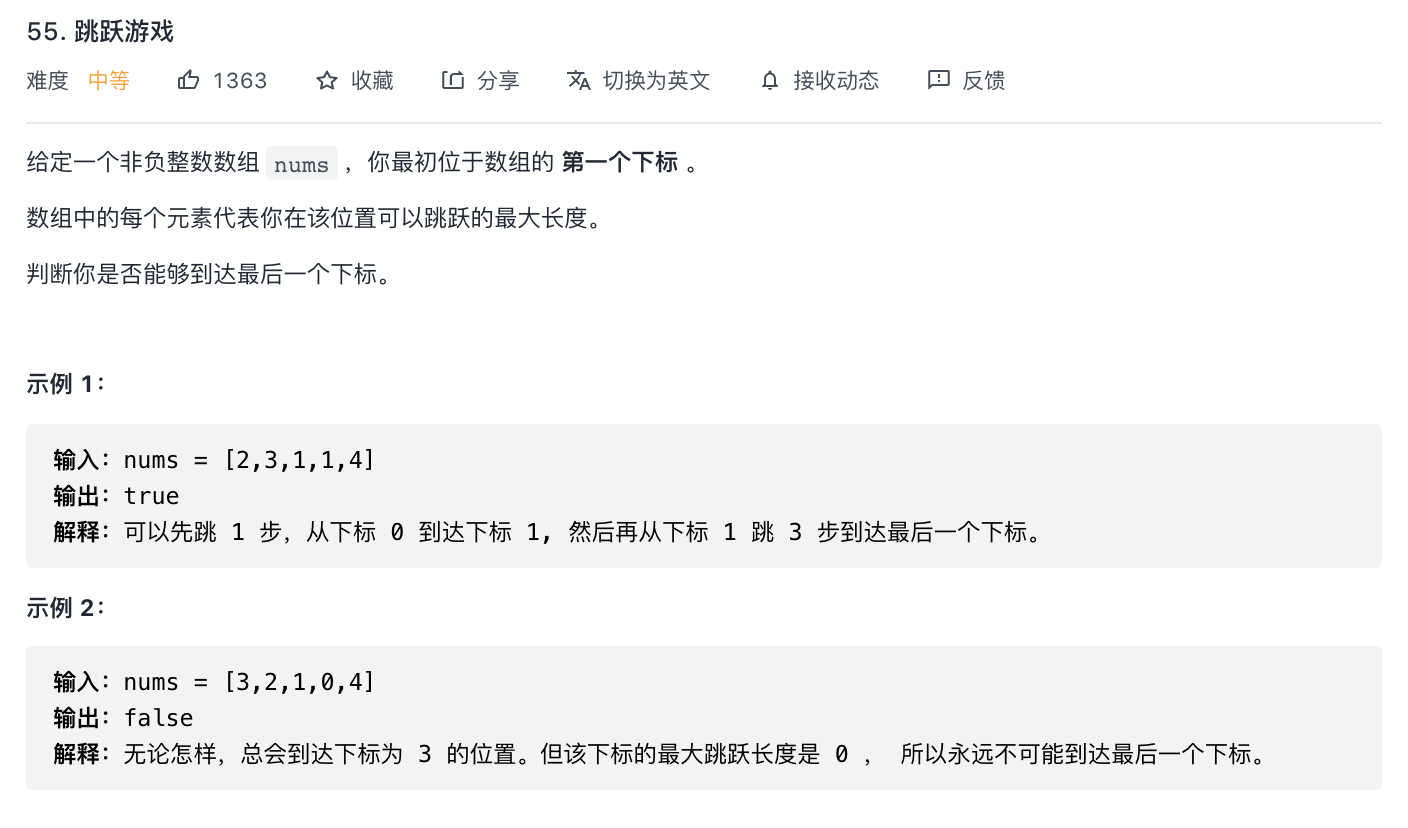
image.png
题意分析：

  • 从数组下表开始跳跃，判断最终是否能够跳跃到数组最后一个节点。

解题思路：

  • 贪心思路。每次找到当前位置可跳跃的最远长度，如果存在某个节点能够跳跃到最后，则直接返回 true。
    • 时间复杂度：O(n)。最坏情况下需要遍历数组所有元素。
    • 空间复杂度：O(1)。需要常量元素记录跳跃的最长距离。
  • 动态规划。动态规划的核心就在dp状态数据的构建和转换过程的转换，动规分为只依赖前一个dp状态和依赖前面所有dp状态，本题属于后者。当前节点能否跳跃到最后节点，需要判断前面所有节点是否存在能够跳跃到最后节点的。
    • 时间复杂度：O(nlog(n))。每个位置的dp数组依赖前面所有位置的dp信息。
    • 空间复杂度：O(n)。需要额外的dp数组记录是否能够跳跃到最后节点。

注意点：

  • 如何将第一种方法理解为贪心算法？

扩展：
代码：

  1.     /**
  2.      * 贪心算法，每次找到当前位置能 jump 的最大距离
  3.      * @param nums
  4.      * @return
  5.      */
  6.     public boolean canJump(int[] nums) {
  7.         int n = nums.length;
  8.         int fastest = 0;
  9.         for (int i = 0; i < n - 1; i++) {
  10.             fastest = Math.max(fastest, i + nums[i]);
  11.             System.out.println("fastest = " + fastest + "; i = " + i);
  12.             if (fastest <= i) return false;
  13.         }
  14.         return fastest >= n - 1;
  15.     }
  17.     /**
  18.      * 动态规划。
  19.      *  1、dp 数组。记录每个位置能否到达最后位置。
  20.      *  2、状态转换。什么情况下会触发状态转换。
  21.      *  3、base case。
  22.      *  4、求解。dp[len - 1]
  23.      * @param nums
  24.      * @return
  25.      */
  26.     public boolean canJump(int[] nums) {
  27.         int n = nums.length;
  28.         // 状态数组。记录每个节点是否能够跳跃到最后节点
  29.         boolean[] dp = new boolean[n];
  31.         // base case
  32.         dp[0] = true;
  34.         for (int i = 1; i < n; i++) {
  35.             // 判断从 dp[0~i-1] 中能够跳跃到最后节点的节点开始（即当前状态和前面多个状态有关）
  36.             for (int j = 0; j < i; j++) {
  37.                 // 判断前面所有位置时，一个条件是前面位置能够到达，另一个条件是能跳过当前节点
  38.                 if (dp[j] && j + nums[j] >= i) {
  39.                     dp[i] = true;
  40.                     break;
  41.                 }
  42.             }
  43. //            System.out.println("i = " + i + "; dp[i] = " + dp[i]);
  44.         }
  46.         // 求解（动规需要遍历完整个数组）
  47.         return dp[n - 1];
  48.     }

*45-跳跃游戏 II

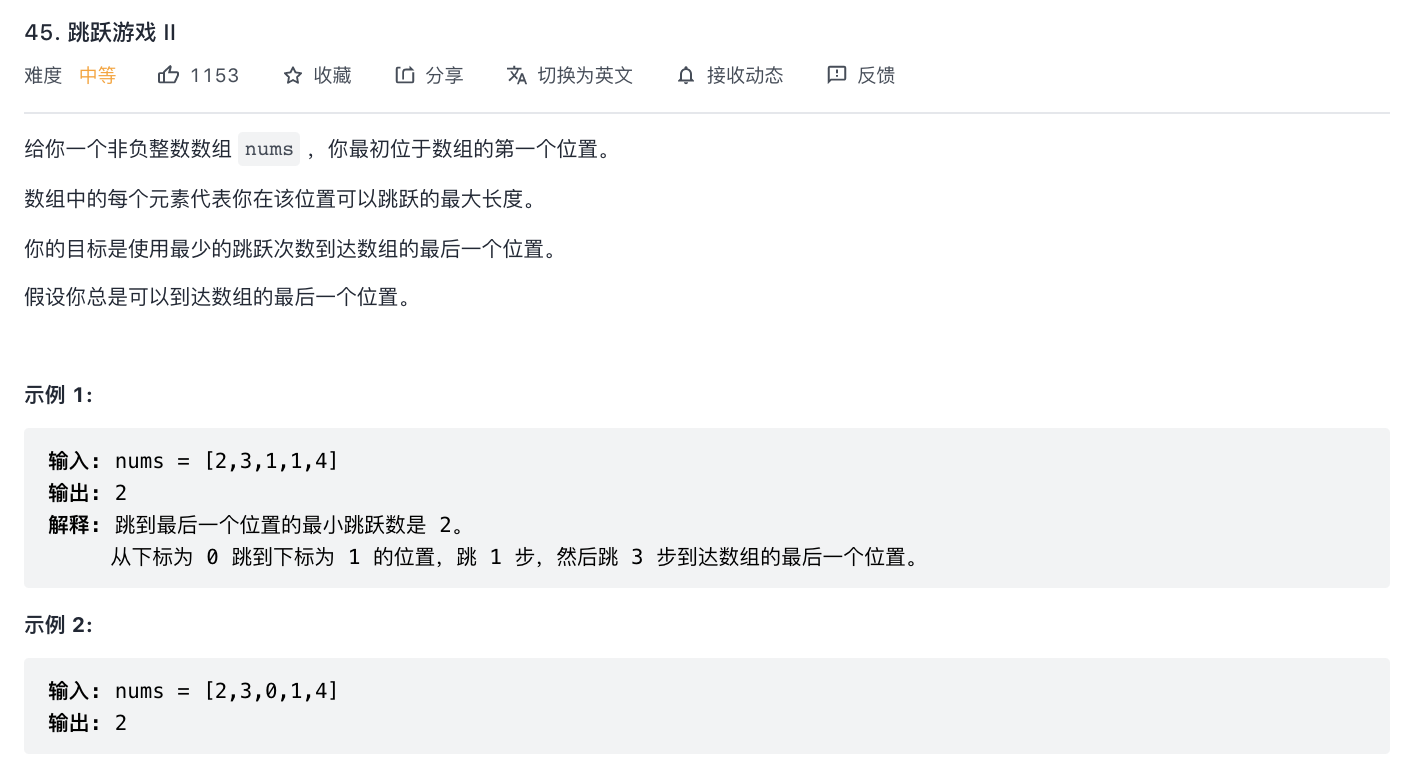
image.png
题意分析：
解题思路：

  • 贪心算法。每个更新跳跃区间，区间更新即为一次 jump，直到区间中包含最后一个位置（索引），表示该区间是上一跳的最远距离，此时结束即可。
  • 优化后的贪心。每次只更远跳跃的最远距离（即只保留右区间），如果抵达了右区间，则更新最区间距离。

注意点：
扩展：
代码：

  1.     /**
  2.      * 贪心算法：每次更新跳跃区间
  3.      * @param nums
  4.      * @return
  5.      */
  6.     public int jump(int[] nums) {
  7.         int n = nums.length;
  8.         int start = 0, end = 0; // [0,0]
  9.         int fastest = 0;
  10.         int step = 0;
  11.         while (end < n - 1) {
  12.             // 每次能跳跃的区间
  13.             for (int i = start; i <= end; i++) {
  14.                 fastest = Math.max(fastest, i + nums[i]);
  15.             }
  16.             // 更新区间左右值
  17.             start = end + 1;
  18.             end = fastest;
  19.             step++;
  20.             System.out.println("start = " + start + "; end = " + end);
  21.         }
  22.         return step;
  23.     }
  25.     /**
  26.      * 优化后的贪心算法，每次更新跳跃到最远距离
  27.      * @param nums
  28.      * @return
  29.      */
  30.     public int jump2(int[] nums) {
  31.         int n = nums.length;
  32.         int fastest = 0;
  33.         // 跳跃最远位置的 index
  34.         int end = 0;
  35.         int step = 0;
  36.         for (int i = 0; i < n - 1; i++) {
  37.             // 每次能跳跃的最远距离
  38.             fastest = Math.max(fastest, i + nums[i]);
  39.             // 到达跳跃最远距离的边界
  40.             if (end == i) {
  41.                 end = fastest;
  42.                 step++;
  43.             }
  44.             System.out.println("i = " + i + "; fastest = " + fastest + "; end = " + end + "; step = " + step);
  45.         }
  46.         return step;
  47.     }

134-加油站

image.png
题意分析：

  • 从某个位置出发，根据加油和耗油判断能否回到远点。

解题思路：

  • 暴力解法。直接判断每个节点能否回到远点。
    • 时间复杂度：O(n^2)
  • 贪心解法。转换为一维数组，判断从某个位置出发，走到的任何节点油箱容量均大于等于0。

注意点：
扩展：
代码：

  1.     /**
  2.      * 暴力破解：
  3.      *  遍历每个 gas[i] >= cost[i] 的 gas，判断是否能够回到原点。
  4.      * @param gas
  5.      * @param cost
  6.      * @return
  7.      */
  8.     public int canCompleteCircuit2(int[] gas, int[] cost) {
  9.         int n = gas.length;
  10.         for (int start = 0; start < n; start++) {
  11.             if (gas[start] < cost[start]) {
  12.                 continue;
  13.             }
  14.             // 每次从新的节点出发油箱容量 tank 均为0
  15.             int tank = 0;
  16.             for (int step = 0; step < n; step++) {
  17.                 // 表示每次从 start 节点出发
  18.                 int i = (start + step) % n;
  19.                 tank += gas[i];
  20.                 tank -= cost[i];
  21.                 if (tank < 0) break;
  22.             }
  23.             if (tank >= 0) return start;
  24.         }
  25.         return -1;
  26.     }
  28.     /**
  29.      * 贪心解法
  30.      *  1、把 gas[i] - cost[i] 组成一个新的数组，
  31.      *    目标是找到一个起点，出发一圈后回到起点的过程中油箱容量 tank 一直大于等于0。
  32.      *    gas=[1,2,3,4,5], cost=[3,4,5,1,2] 问题转换为 gap = [-2, -2, -2, 3, 3] 问题。
  33.      *  2、如果从 i 走到 j 出现 tank < 0，那么从 [i,j] 之间任意一个节点出发 tank 都小于 0。
  34.      * @param gas
  35.      * @param cost
  36.      * @return
  37.      */
  38.     public int canCompleteCircuit(int[] gas, int[] cost) {
  39.         int n = gas.length;
  40.         int[] gap = new int[n];
  41.         int sum = 0;
  42.         for (int i = 0; i < n; i++) {
  43.             gap[i] = gas[i] - cost[i];
  44.             sum += gap[i];
  45.         }
  46.         if (sum < 0) {
  47.             return -1;
  48.         }
  49.         System.out.println(Arrays.toString(gap));
  51.         int tank = 0, start = 0;
  52.         for (int i = 0; i < n; i++) {
  53.             tank += gap[i];
  54.             // i 走到 j 不满足条件，那么 [i,j] 直接都不满足
  55.             if (tank < 0) {
  56.                 tank = 0;
  57.                 start = i + 1;
  58.             }
  59.         }
  60.         return start;
  61.     }

区间问题（贪心）

435-无重叠区间（贪心+排序/动态+二分）

image.png
题意分析：

  • 求出最大无重复区间，然后剩下的就是重复区间。

解题思路：

  • 贪心算法。贪心算法求区间问题每次都是先对区间右边界排序，然后比较当前左区间与上一区间的右边界，贪心之处就在于之比较最大值（或最远值，比如跳跃游戏）。
  • 动态规划。动态规划求区间问题需要先对左区间排序，然后比较当前区间左边界与上一区间右边界是否重叠，逐一求每个区间的最大无重叠区间。

注意点：
扩展：
代码：

  1.     /**
  2.      * 贪心思想。
  3.      *  1、先对区间右边界 end 升序排序
  4.      *  2、比较当前区间右边界与下一区间的左边界，不重叠则不重叠区间+1
  5.      * @param intervals
  6.      * @return
  7.      */
  8.     public int eraseOverlapIntervals(int[][] intervals) {
  9.         Arrays.sort(intervals, new Comparator<int[]>() {
  10.             @Override
  11.             public int compare(int[] o1, int[] o2) {
  12.                 return o1[1] - o2[1];
  13.             }
  14.         });
  15.         for (int i = 0; i < intervals.length; i++) {
  16.             System.out.println(Arrays.toString(intervals[i]));
  17.         }
  18.         int ans = 1;
  19.         int end = intervals[0][1];
  20.         for (int i = 1; i < intervals.length; i++) {
  21.             // start >= end
  22.             if (intervals[i][0] >= end) {
  23.                 ans++;
  24.                 end = intervals[i][1];
  25.             }
  26.         }
  27.         return intervals.length - ans;
  28.     }
  30.     /**
  31.      * 动态规划（超出时间限制）
  32.      *  1、先按区间 start 排序（为了方便当前区间 start 与上一区间 end 判断）
  33.      *  2、dp[i]：每个一元数组的最大无重叠子区间
  34.      *  3、当前状态与前面多个状态均有关
  35.      * @param intervals
  36.      * @return
  37.      */
  38.     public int eraseOverlapIntervals2(int[][] intervals) {
  39.         int n = intervals.length;
  40.         // 状态数据
  41.         int[] dp = new int[n];
  43.         // base case：默认都有一个无重叠区间
  44.         Arrays.fill(dp, 1);
  46.         Arrays.sort(intervals, new Comparator<int[]>() {
  47.             @Override
  48.             public int compare(int[] o1, int[] o2) {
  49.                 return o1[0] - o2[0];
  50.             }
  51.         });
  53.         for (int i = 0; i < intervals.length; i++) {
  54.             System.out.println(Arrays.toString(intervals[i]));
  55.         }
  57.         // 状态转换
  58.         for (int i = 0; i < n; i++) {
  59.             // dp 数组和前面多个状态有关
  60.             for (int j = 0; j < i; j++) {
  61.                 // 更新重叠子区间条件判断
  62.                 if (intervals[i][0] >= intervals[j][1]) {
  63.                     dp[i] = Math.max(dp[i], dp[j] + 1);
  64.                 }
  65.             }
  66.         }
  68.         // 求解
  69.         return n - Arrays.stream(dp).max().getAsInt();
  70.     }

452-用最少数量的箭引爆气球-无重复区间（贪心+排序）

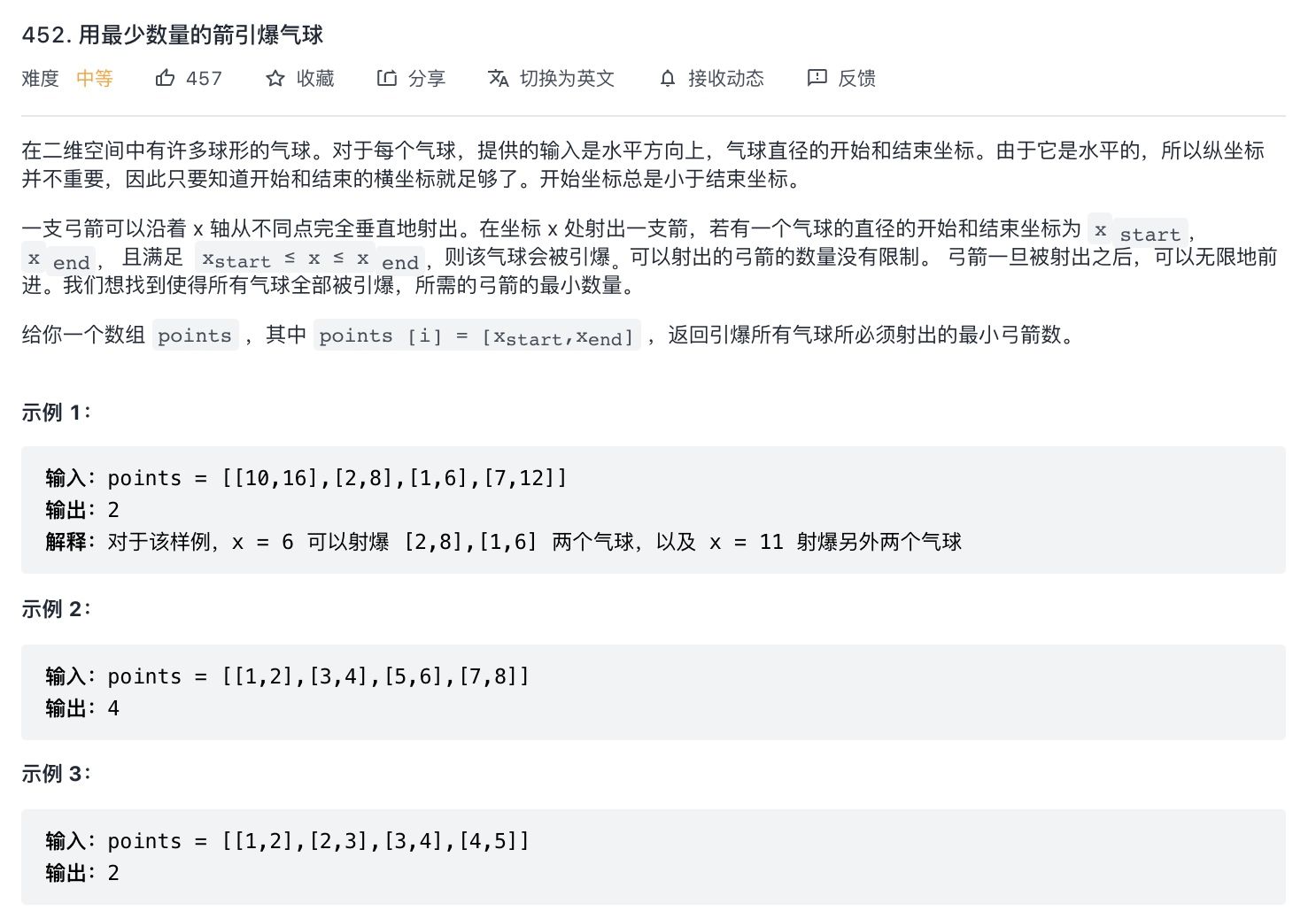
image.png
题意分析：

  • 重复区间用一支箭射穿即可，说明问题是要求无重复区间的数量。

解题思路：

  • 贪心+排序。问题本质就是求最大无重复区间的数量，每个无重复区间用一支箭射穿即可。

注意点：

  • 排序时直接返回 o1[1] - o2[1] 时要考虑减法的结果是否超过 INT 限制，会导致排序结果混乱。

扩展：
代码：

  1.     /**
  2.      * 贪心+排序。
  3.      *  问题本质就是求最大无重复区间的数量，每个无重复区间用一支箭射穿即可。
  4.      * @param points
  5.      * @return
  6.      */
  7.     public int findMinArrowShots(int[][] points) {
  8.         int n = points.length;
  9.         // 按区间end升序排序
  10.         Arrays.sort(points, new Comparator<int[]>() {
  11.             @Override
  12.             public int compare(int[] o1, int[] o2) {
  13.                 // 排序时直接返回 o1[1]-o2[1] 要考虑返回结果是否超出INT限制
  14.               if (o1[1] > o2[1])
  15.                 return 1;
  16.               else if (o1[1] < o2[1])
  17.                 return -1;
  18.               else
  19.                     return 0;
  20.             }
  21.         });
  22.         int end = points[0][1];
  23.         int ans = 1;
  24.         for (int i = 1; i < n; i++) {
  25.             // 边界如果相等则可以处理两个区间，所以这里不用等于号
  26.             if (points[i][0] > end) {
  27.                 ans++;
  28.                 end = points[i][1];
  29.             }
  30.         }
  31.         return ans;
  32.     }

1024-视频拼接（贪心+排序）

image.png
题意分析：

  • 选取最少的区间数，使得区间完全包含 [0,T] 。

解题思路：

  • 贪心+排序。[0,1], [0,5], [0,9] 按照贪心策略，肯定是优先选择 [0,9] 这个大区间，才可能使得最终选择的区间数最少（这便是贪心最有选择策略）。所以这里需要先对数组排序，先按 start 升序排序，再按 end 降序排序。然后判断区间的包含关系更新区间。

注意点：

  • 要注意这里区间可能划分小了，比如 [0,4], [2,6], [4,7]，两个区间能解决的事就不用三个区间解决，因为还要判断上个区间的结束 pre_end 值，便于更新区间数统计。

扩展：

  • 能否打印出对应的区间？

代码：

  1.     public int videoStitching(int[][] clips, int time) {
  2.         int n = clips.length;
  3.         // 对数组进行排序，先根据 start 升序排序，再按照 cur_end 降序排序
  4.         Arrays.sort(clips, new Comparator<int[]>() {
  5.             @Override
  6.             public int compare(int[] o1, int[] o2) {
  7.                 if (o1[0] == o2[0])
  8.                     return o2[1] - o1[1];
  9.                 return o1[0] - o2[0];
  10.             }
  11.         });
  12.         for (int i = 0; i < n; i++) {
  13.             System.out.println(Arrays.toString(clips[i]));
  14.         }
  15.         int step = 1;
  16.         int pre_end = 0, cur_end = clips[0][1];
  17.         // 无法从 0 左区间开始，直接返回无法剪辑
  18.         if (clips[0][0] > 0 ) return -1;
  19.         // 如果第一个区间满足要求，则直接返回
  20.         if (cur_end >= time) return step;
  22.         LinkedList<int[]> list = new LinkedList<>();
  23.         list.add(new int[]{clips[0][0], clips[0][1]});
  25.         for (int i = 1; i < n; i++) {
  26.             // 下一区间跨越上一区间的end边界
  27.             if (clips[i][0] <= cur_end && clips[i][1] > cur_end) {
  28.                 // step 更新条件很关键。比如 [0,4],[2,6],[4,7],[6,9]，其实只要三个区间就能满足要求 [2,6]是多余的
  29.                 // 因此，这里要记录上一次区间的结束 pre_end 值，只有超过 pre_end 值才更新 step
  30.                 if (clips[i][0] > pre_end) {
  31.                     step++;
  32.                     pre_end = cur_end;
  33.                 } else {
  34.                     // 说明上一次区间冗余，需要删除掉
  35.                     list.pollLast();
  36.                 }
  37.                 cur_end = clips[i][1];
  38.                 list.add(new int[]{clips[i][0], clips[i][1]});
  39.                 if (cur_end >= time) break;
  40.             }
  41.         }
  42.         if (cur_end >= time) return step;
  43.         return -1;
  44.     }

1288-删除被覆盖区间（区间覆盖）

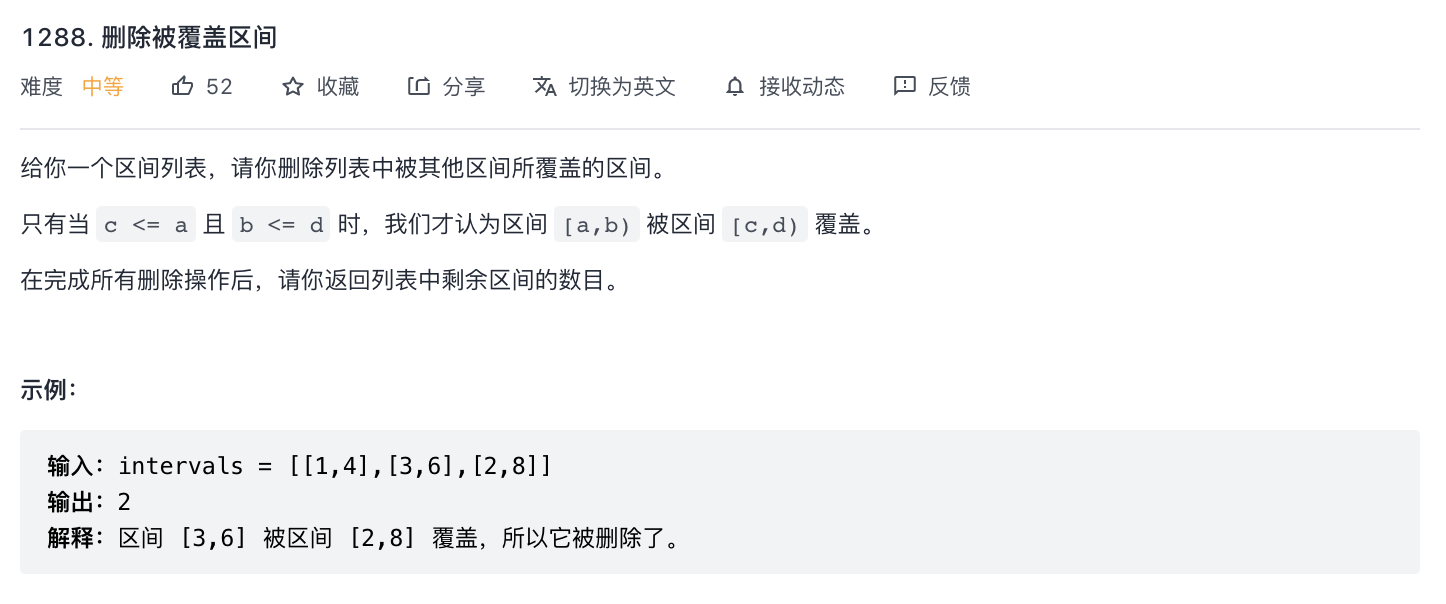
image.png
题意分析：

  • 对多个区间中包含的区间进行去重，只保留不重复且区间范围大的区间。

解题思路：

  • 排序+贪心。先对区间 start 升序和 end 降序，然后画图确认区间覆盖的条件进行过滤。

注意点：
扩展：
代码：

  1.     /**
  2.      * 区间覆盖问题
  3.      *  1、排序。先对区间 start 升序排序，再对区间 end 降序排序。
  4.      *  2、画图。判断什么时候覆盖什么是不覆盖。
  5.      * @param intervals
  6.      * @return
  7.      */
  8.     public int removeCoveredIntervals(int[][] intervals) {
  9.         int n = intervals.length;
  10.         Arrays.sort(intervals, new Comparator<int[]>() {
  11.             @Override
  12.             public int compare(int[] o1, int[] o2) {
  13.                 if (o1[0] != o2[0])
  14.                     return o1[0] - o2[0];
  15.                 return o2[1] - o1[1];
  16.             }
  17.         });
  19.         for (int i = 0; i < n; i ++) {
  20.             System.out.println(Arrays.toString(intervals[i]));
  21.         }
  22.         int left = Integer.MAX_VALUE, right = Integer.MIN_VALUE;
  23.         int res = 0;
  24.         for (int i = 0; i < n; i++) {
  25.             if (!(intervals[i][0] >= min && intervals[i][1] <= max)) {
  26.                 res++;
  27.                 left = intervals[i][0];
  28.                 right = intervals[i][1];
  29. //                System.out.println(left + "; " + right);
  30.             }
  31.         }
  32.         return res;
  33.     }

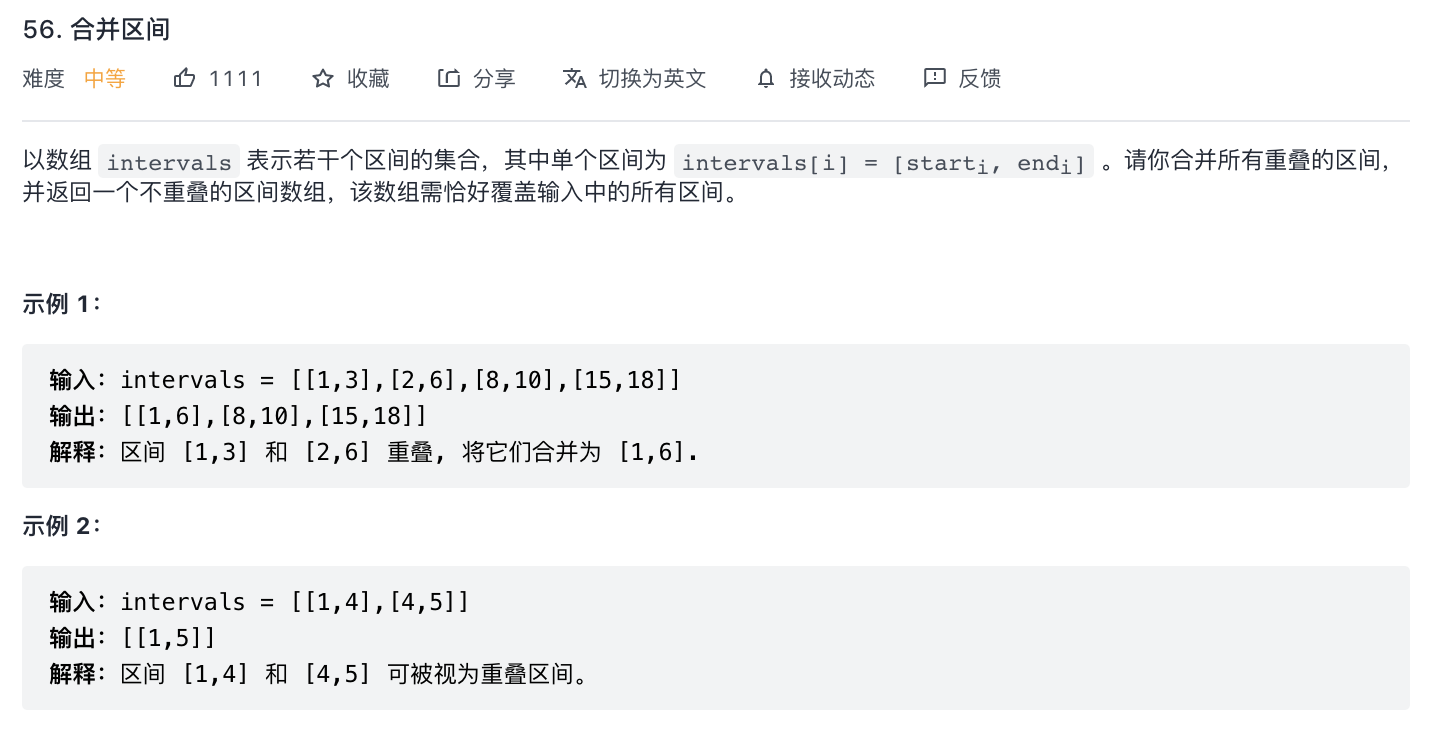
56-合并区间（区间合并）

image.png
题意分析：

  • 对存在重叠或连续的区间进行合并，合并成一个大的区间。

解题思路：

  • 排序+贪心。先对区间 start 升序和 end 降序，然后画图确认区间合并的条件进行过滤。

注意点：

  • 返回二维数组的数据结构选取，以及如何返回结果。

扩展：
代码：

  1.     /**
  2.      * 区间合并问题
  3.      *  1、排序。先对区间 start 升序排序，再对区间 end 降序排序。
  4.      *  2、画图。判断什么时候需要更新合并 list，什么时候更新 list 右区间。
  5.      *  3、数据结构选取。List<int[]> list，返回 list.toArray(new int[list.size][]);
  6.      * @param intervals
  7.      * @return
  8.      */
  9.     public int[][] merge(int[][] intervals) {
  10.         int n = intervals.length;
  11.         Arrays.sort(intervals, new Comparator<int[]>() {
  12.             @Override
  13.             public int compare(int[] o1, int[] o2) {
  14.                 if (o1[0] != o2[0])
  15.                     return o1[0] - o2[0];
  16.                 return o2[1] - o1[1];
  17.             }
  18.         });
  20. //        for (int i = 0; i < n; i ++) {
  21. //            System.out.println(Arrays.toString(intervals[i]));
  22. //        }
  23.         int left = 0, right = 0;
  24.         List<int[]> list = new ArrayList<>();
  25.         for (int i = 0; i < n; i++) {
  26.             left = intervals[i][0];
  27.             right = intervals[i][1];
  28.             // 不需要进行合并操作的情况
  29.             if (list.size() == 0 || list.get(list.size() - 1)[1] < left) {
  30.                 list.add(new int[]{left, right});
  31.             }
  32.             if (left <= list.get(list.size() - 1)[1] && right >= list.get(list.size() - 1)[1]) {
  33.                 // 更新右区间
  34.                 list.get(list.size() - 1)[1] = right;
  35.             }
  36.         }
  37.         return list.toArray(new int[list.size()][]);
  38.     }

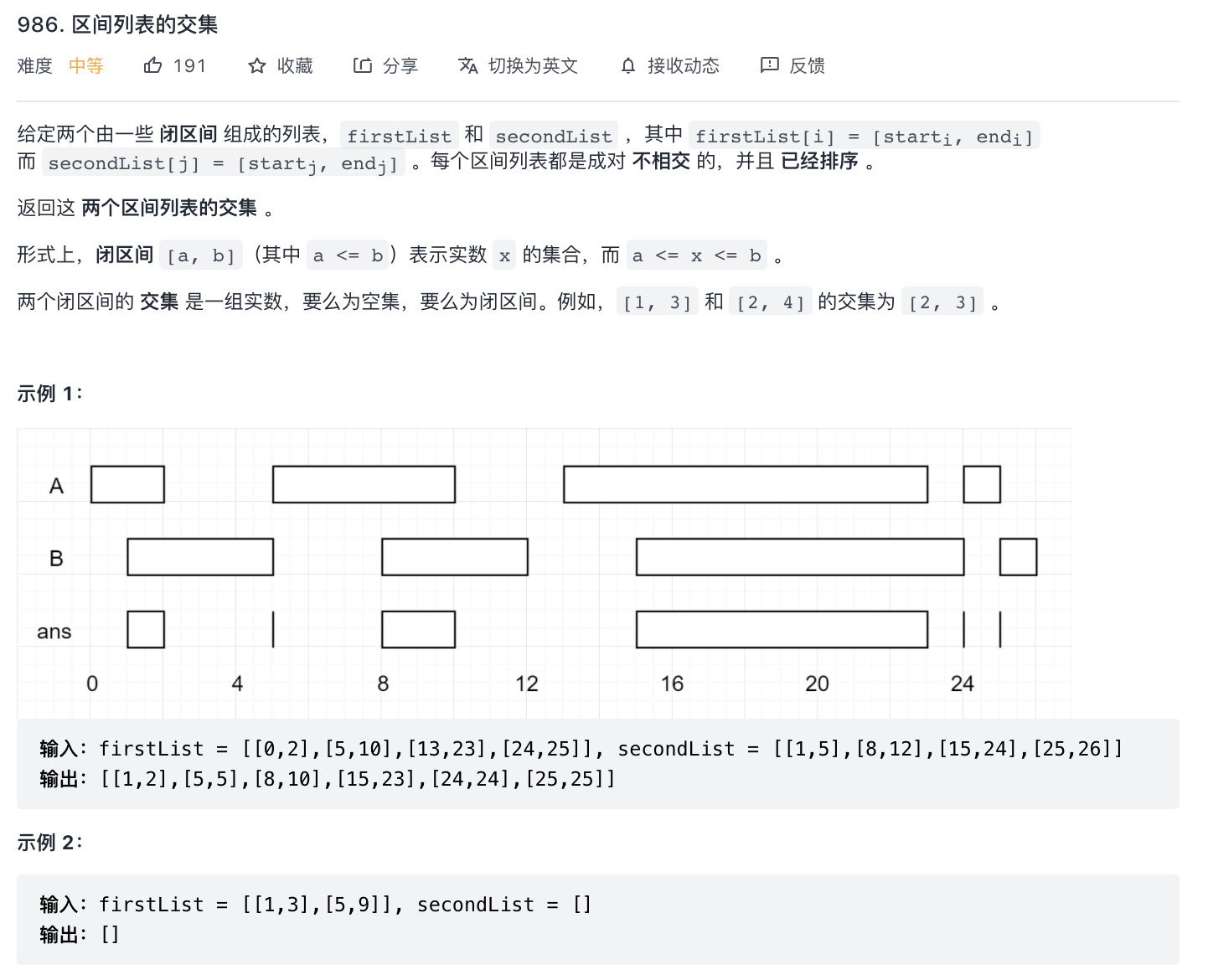
986-区间列表交集（区间交集）

image.png
题意分析：

  • 求两个区间的交集，单个元素存在交集也要输出。

解题思路：

  • 双指针。排序+画图，由于区间已排序，直接画图通过两个指针分别对比两个区间的元素，如果存在交集则添加到 list，如果没交集则左右指针依次前进。

注意点：

  • 左右指针的前进条件，什么时候前进 left，什么时候前进 right。
  • while 循环的退出条件，如果有一个指针扫描区间结束，则一定不存在交集。

扩展：
代码：

  1.     /**
  2.      * 区间已排序，直接画图判断更新交集区间。
  3.      * @param firstList
  4.      * @param secondList
  5.      * @return
  6.      */
  7.     public int[][] intervalIntersection(int[][] firstList, int[][] secondList) {
  8.         int m = firstList.length, n = secondList.length;
  9.         List<int[]> list = new ArrayList<>();
  10.         int left = 0, right = 0;
  11.         while (left < m && right < n) {
  12.           // 取两个区间的左右值
  13.             int low = Math.max(firstList[left][0], secondList[right][0]);
  14.             int high = Math.min(firstList[left][1], secondList[right][1]);
  15.             // 区间存在交集
  16.             if (low <= high) {
  17.                 list.add(new int[]{low, high});
  18.             }
  19.             if (firstList[left][1] < secondList[right][1]) {
  20.                 left++;
  21.             } else {
  22.                 right++;
  23.             }
  24.         }
  25.         return list.toArray(new int[list.size()][]);
  26.     }

未分类

70-爬楼梯

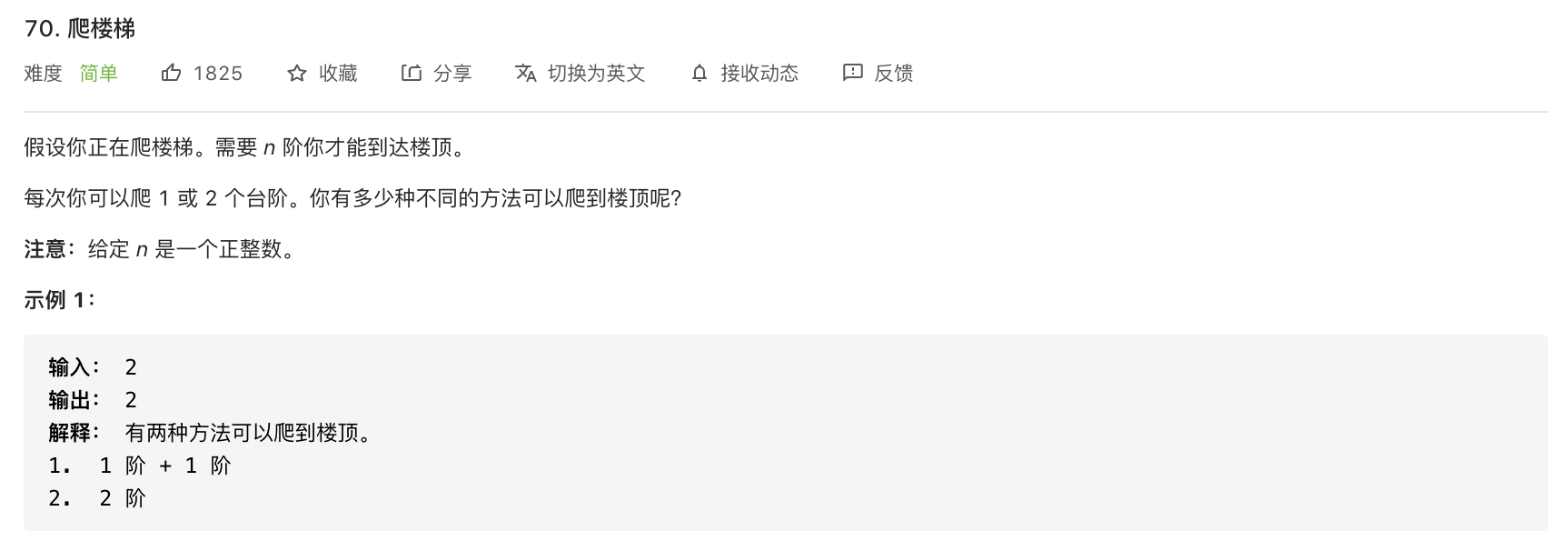
image.png
题意分析：
解题思路：
注意点：
扩展：
代码：

  1.     public int climbStairs(int n) {
  2.         if (n == 1) return 1;
  3.         if (n == 2) return 2;
  5.         // 状态数组
  6.         int[] dp = new int[n+1];
  8.         // base case. dp[0] ignore
  9.         dp[1] = 1;
  10.         dp[2] = 2;
  12.         // 状态转换
  13.         for (int i = 3; i <= n; i++) {
  14.             dp[i] = dp[i-1] + dp[i-2];
  15.         }
  17.         // 求解
  18.         return dp[n];
  19.     }

模版

题意分析：
解题思路：
注意点：
扩展：
代码：