排序算法

衡量排序算法的优劣：

1.时间复杂度：分析关键字的比较次数和记录的移动次数
2.空间复杂度：分析排序算法中需要多少辅助内存
3.稳定性：若两个记录A和B的关键字值相等，但排序后A、B的先后次序保持不变，则称这种排序算法是稳定的。

十大内部排序算法

选择排序
Ø 直接选择排序、堆排序
交换排序
Ø 冒泡排序、快速排序
插入排序
Ø 直接插入排序、折半插入排序、Shell排序
归并排序
桶式排序
基数排序

算法的5大特征

输入（Input）有0个或多个输入数据，这些输入必须有清楚的描述和定义
输出（Output）至少有1个或多个输出结果，不可以没有输出结果
有穷性（有限性，Finiteness）算法在有限的步骤之后会自动结束而不会无限循环，并且每一个步骤可以在可接受的时间内完成
确定性（明确性，Definiteness）算法中的每一步都有确定的含义，不会出现二义性
可行性（有效性，Effectiveness）算法的每一步都是清楚且可行的，能让用户用纸笔计算而求出答案

冒泡排序:

比较相邻的元素。如果第一个比第二个大（升序），就交换他们两个。
2. 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步
做完后，最后的元素会是最大的数。
3. 针对所有的元素重复以上的步骤，除了最后一个。
4. 持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较为止。 ```java public static void main(String[] args) {
```
 int[] arr = new int[]{43,4,26,46,7,85,1,858,48,51,75,25,99};
 for(int i=0;i<arr.length-1;i++){
     for(int j=0;j<arr.length-i-1;j++){
         if(arr[j]>arr[j+1]){
             int temp = arr[j];
             arr[j] = arr[j+1];
             arr[j+1] = temp;
         }
     }
 }
```


- 快速排序
是迄今为止所有内排序算法中速度最快的一种。冒泡排序的升级版，交换排序的一种。<br />快速排序的时间复杂度为O(nlog(n))。
- **排序思想：**
-  从数列中挑出一个元素，称为"基准"（pivot），
- 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区结束之后，该基准就处于数列的中间位置。这个称为分区（partition）操作。
-  递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。
- 递归的最底部情形，是数列的大小是零或一，也就是永远都已经被排序好了。虽然一直递归下去，但是这个算法总会结束，因为在每次的迭代iteration）中，它至少会把一个元素摆到它最后的位置去。
```java
        // 交换函数
        private static void swap(int[] array, int i, int j) {
            int temp = array[i];
            array[i] = array[j];
            array[j] = temp;
        }
        private static void subSort(int[] array, int start, int end) {
            //左右指针不相等就继续排序
            if (start < end) {
                // 基准---数组首元素
                int pivot = array[start];
                // 待划分区域首元素
                int leftPoint = start;
                // 待划分区域尾元素----加一是因为下方用的是--rightPoint
                int rightPoint = end + 1;
                while (true) {
                    //当左指针还没有移到最右边且指针所指元素小于基准数,继续下次循环
                    //一直到左指针所指元素大于基准数,记录现在的指针
                    while (leftPoint < end && array[++leftPoint] <= pivot)
                        ;
                    //当右指针还没有移到最左边且指针所指元素大于于基准数,继续下次循环
                    //一直到右指针所指元素小于基准数,记录现在的指针
                    while (rightPoint > start && array[--rightPoint] >= pivot)
                        ;
                    //记录的左指针是大于基准数的元素
                    //记录的右指针是小于基准数的元素
                    //如果此时左指针在右指针左边,交换这两个元素位置
                    //否则跳出循环----因为此时leftPoint+1=rightPoint,左右指针已经将所有元素已遍历
                    if (leftPoint < rightPoint) {
                        swap(array, leftPoint, rightPoint);
                    } else {
                        break;
                    }
                }
                //交换本轮排序的基准数和最后发现的小于基准数的元素,
                //使小于基准数的元素位于左边,大于基准数的元素位于右边
                swap(array, start, rightPoint);
                //左区域进行下一次排序
                subSort(array, start, rightPoint - 1);// 递归调用
                //右区域进行下一次排序
                subSort(array, rightPoint + 1, end);
            }
        }
        public static void quickSort(int[] array) {
            subSort(array, 0, array.length - 1);// 传参----目的数组地址-首指针-尾指针
        }
        public static void main(String[] args) {
            int[] array = { 91, -16, 30, 23, -30, -49, 25, 21, 30 };
            System.out.println("排序之前：\n" + java.util.Arrays.toString(array));
            quickSort(array);// 传参--目的数组地址
            System.out.println("排序之后：\n" + java.util.Arrays.toString(array));
        }
    }

数组中指定元素的查找：搜索、检索

线性查找：

实现思路：通过遍历的方式，一个一个的数据进行比较、查找。
适用性：具有普遍适用性。

二分法查找：

实现思路：每次比较中间值，折半的方式检索。
适用性：（前提：数组必须有序）

        int[] arr = new int[]{-84,-79,-36,-8,0,8,12,26,34,48,57,61,85,91,256,364};
        int headPoint = 0;
        int endPoint = arr.length-1;    
        int aimNumber = 91;
        while(headPoint <= endPoint){
            int middle = (headPoint + endPoint)/2;
            if(arr[middle] == aimNumber){
                System.out.println("找到了!!!第"+(middle+1)+"个元素");
                break;
            }else if(arr[middle] > aimNumber){//在左边
                endPoint = middle - 1;//当未查询到时用于跳出循环
            }
            else{//在右边
                headPoint = middle + 1;//当未查询到时用于跳出循环
            }
        }
        if(headPoint > endPoint){
            System.out.println("未找到!!!");
        }

排序算法性能对比 :

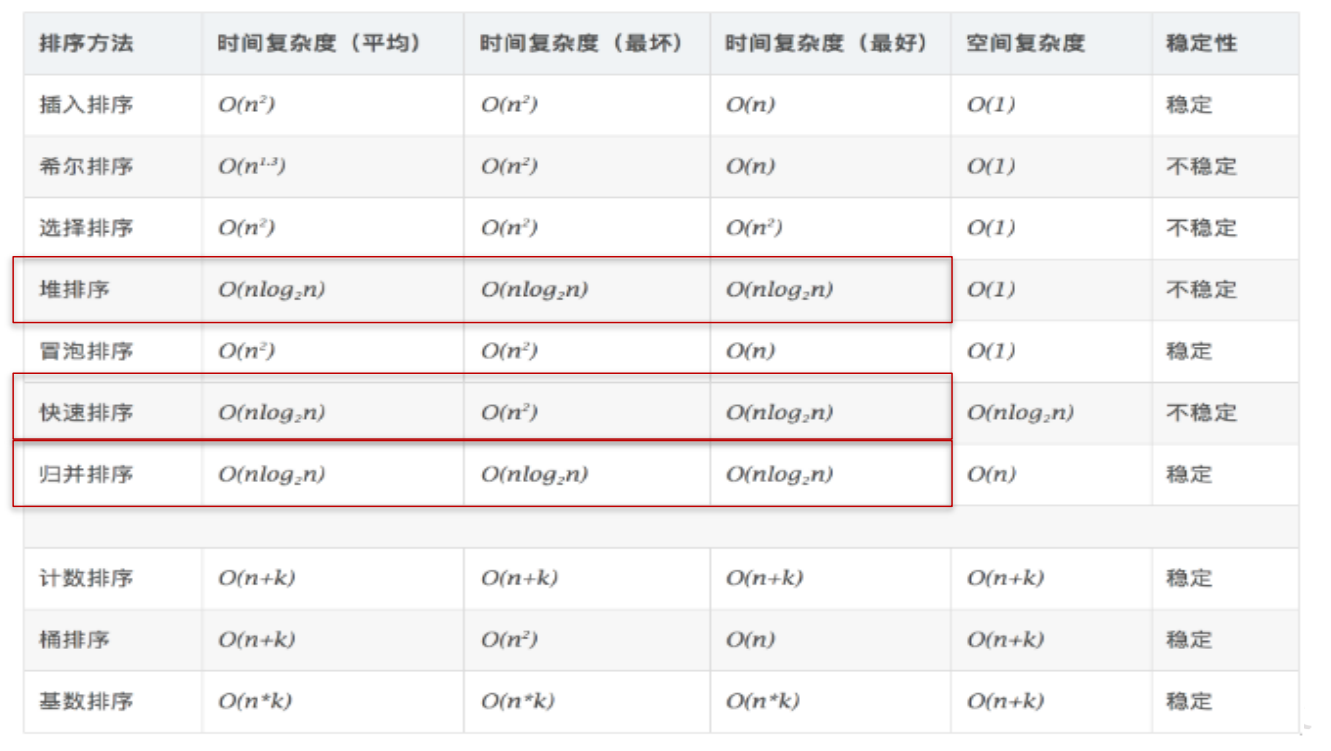
从平均时间而言：快速排序最佳。但在最坏情况下时间性能不如堆排序和归并排序。
从算法简单性看：由于直接选择排序、直接插入排序和冒泡排序的算法比较简单，将其认为是简单算法。对于Shell排序、堆排序、快速排序和归并排序算法，其算法比较复杂，认为是复杂排序。
从稳定性看：直接插入排序、冒泡排序和归并排序时稳定的；而直接选择排序、快速排序、 Shell排序和堆排序是不稳定排序
从待排序的记录数n的大小看，n较小时，宜采用简单排序；而n较大时宜采用改进排序。

排序算法的选择
若n较小(如n≤50)，可采用直接插入或直接选择排序。当记录规模较小时，直接插入排序较好；否则因为直接选择移动的记录数少于直接插入，应选直接选择排序为宜。
若文件初始状态基本有序(指正序)，则应选用直接插入、冒泡或随机的快速排序为宜；
若n较大，则应采用时间复杂度为O(nlgn)的排序方法：快速排序、堆排序或归并排序。

JavaSE 高级进阶

数组有关算法

排序算法

数组中指定元素的查找：搜索、检索

排序算法性能对比 :

排序算法的选择